基于强化学习的列车驾驶曲线节能优化算法

黄 畅，姜辰宇，邢昕铨

（1.北京交通大学，北京 100044；2.华南理工大学，广东 广州 510641）

1 基于DQN实现最优化驾驶策略

1.1 列车动力学模型

列车动力学模型可以基于牛顿第二定律来建立。

式中，uf(x)为牵引力系数；F(v)为最大牵引力；ub(x)为制动力系数；B(v)为最大制动力；R(v)为行车阻力；G(x)为坡度阻力。

行车阻力满足戴维斯方程如公式（2）所示。

式中，a，b，c和列车车轮与轨道之间的摩擦系数相关。

基于列车动力学模型，列车的目标函数与限制条件如公式（3）和公式（4）所示。从列车的目标函数可以看出，当距离是一定的时候，需要改变的变量是力的大小，可以是牵引力也可以是制动力。此外需要根据其限制条件，定义起始状态、终止状态以及行驶状态，在设置奖励的时候也需要通过限制条件设置奖励与惩罚。

为了实现在强化学习框架下的最佳列车控制，根据列车动力学模型来定义状态，动作，环境，奖励等必要因素，把火车做出决策的车载控制器定义为智能体；将铁路条件和列车动态特性看作环境速度；将剩余火车的运行时间和位置定义为状态；牵引力和制动力的大小被定义为动作；基于优化目标和约束条件，速度、剩余的运行时间和能量消耗被定义为奖励。环境可以在动作和状态转换之间建立联系，在与智能体互动时，环境以状态和奖赏给予回应，与环境交互后，智能体存储在深度Q网络中学到的知识。

1.2 MDP模型

如果将列车的位置、速度和时间看作是列车的状态，那列车的状态仅和它前一个状态以及驾驶员采取的行为相关，而和之前状态无关。如公式（5）所示，列车运行被分为很多部分。在开始第一个状态后，驾驶员每次选择的行为都会产生下一个状态。

式中，s0是列车的初始状态；sN是终止状态。可以明看出状态si+1只和状态si、动作ai相关。因此，列车运行过程可以看作是典型的马尔科夫决策过程。

1.3 状态

状态的空间表达式可以定义为

式中，k=1，2，…，N-1；sk为第k步状态；pk，vk，tk为列车位于状态sk时，列车的位置、速度和剩余运行时间；Δp为列车状态转移步；VH(pk)为pk位置的最高限速；Tr(pk)为pk位置的最小剩余运行时间；Tm为由列车调度提供的列车计划运行时间。

定义状态的时候，存在三方面的考虑：一是使用剩余运行时间作为状态的一个变量，更契合变化的计划运行时间；二是智能体通过奖励来学习，选择更节能的动作，减少状态的维度，同时提高收敛率；三是动作一般发生在状态转换之间，为了防止在列车运行的过程中发生列车倒车的情况，当列车的速度减少为0的时候，不再采取任何动作，列车终止运行。

每次列车出发到结束存在初始状态s0和最终状态sN，每结束一次运行，再次开启下一次运行，状态回到s0。每次列车运行都会以好的或者坏的结果结束，好的方式意味着列车准时且精准的停车；坏的方式意味着列车倒车，超速或超时。

S+(sN)和S-(sN)分别表示列车结束运行时好的终止状态和坏的终止状态。Pm表示终点站的位置。将列车早于计划时间停靠终点站看作是好的终止状态而非坏的，为了减少能耗，智能体通过学习来减少列车运行时间且保证列车停靠的精确性。

为了提高列车初始状态的多样性以提高理想化的效率，将上一轮列车运行的终止状态的上一步看作为下一轮列车运行的初始状态。因此，初始状态s0可以被定义为

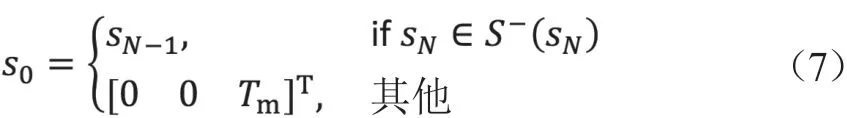
1.4 动作

我们把列车牵引力和制动力的大小看作是动作变量。动作ak-1发生在状态sk-1和sk之间，然后在状态sk时会采取动作ak。根据牵引力和制动力设置的大小，所有动作都从这些力的集合中选择。动作空间可以被定义为A={-M,…,-1,0,1,…,M}。

1.5 奖励

在强化学习中，智能体是围绕奖励来建立的。智能体主要学习如何在保证安全、准时的前提下减少能耗。当列车倒车、超速或超时，设置智能体得到负奖励R-，当列车精确地停在终点站且没有超时时，智能体得到正奖励R+。当列车在行进过程中，智能体得到的奖励为f(ci)，定义为：

式中，i=0,1,…,N-1；ci为状态转移时列车消耗的能量；f(ci)为ci的负相关函数；b,d为不相关系数。可以看出，当能耗ci越大时，f(ci)越小，满足负相关，即当列车耗能越大时，所获得的奖励越小。

1.6 整体结构

图1展示了DQN如何学习列车理想驾驶策略。框图分为两部分：第一部分主要用来生成经验用于训练；另一部分用来训练Q-network。从记忆中随机抽取(s,a,r,s')来对Q-network进行训练。每次更新参数θ时，智能体都会从记忆库D中随机抽取一部分记忆。参数θ通过梯度下降法来更新，然后周期性地更换目标网络的参数。这俩部分同时进行以便实现功能最大化。

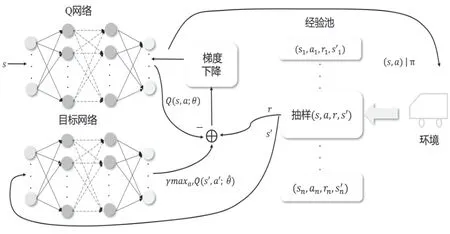
图1 DQN学习列车理想驾驶策略结构图

2 仿真实验

2.1 实验参数

在仿真实验中，列车看作是一个重达200吨的质点，起点站和终点站之间共有1.53千米，每一百米提供一个状态转换点。相关参数如图2所示。

图2 参数图

2.2 仿真结果

（1）探究三种不同的列车运行时间在理想驾驶策略的基础上对列车能耗的影响：方案一(Tm1=100 s)、方案二(Tm2=110 s)、方案三(Tm3=120 s)和方案四(Tm4=130 s)。四种情况下，列车的状态如表1所示。

表1 列车在四种情况下的最终状态

智能体在学习完列车300 000次状态转移步后，从情况一到情况四，平均速度不断减少。在四种情况里面，列车一开始加速，然后滑行一段距离，制动减速只会用于停车的时候。从图3看出，列车在满足准点和安全前提下，列车能耗随着列车计划运行时间的增大而减少。主要原因是随着列车计划运行时间的增加，对于超时的惩罚会减少，所以智能体有更多机会去试错，来自能量消耗的奖励会让列车减少牵引力，使速度更小，能量消耗更少。

图3 列车能耗曲线

第二部分探究神经网络的不同节点数在理想驾驶策略的基础上对列车能耗的影响。共分6种情况来进行比较，从方案一到方案六，每层网络的神经元个数为6、12、18、24、30、36。图4展示Q值的收敛情况。

图4 Q值收敛情况

可以看出，最终收敛步数约在5 000步，然后最终收敛近似动作值都在0到-2间，峰值存在一定差别。得出结论：在其他参数一定的情况下，调节神经网络每层神经元的个数对训练速度的影响不大。

图5 Q值收敛曲线

六种情况下，列车的状态与神经元个数如表2所示。

表2 列车在四种情况下的最终状态

可以看出，列车在满足准点和安全前提下，列车能耗并非根据神经元个数的增加呈现规律性变化，训练效果并非随着神经元的个数增加而变得更好，而是在其中一个值时，训练效果达到顶峰。

3 结束语

本文提供了一种基于强化学习的列车节能优化算法。大部分关于列车运行策略的传统研究都基于给定的模型和固定的参数，这种研究对于像列车运行这种数据量大，在线路参数时常变化的情况是存在很大弊端的。而基于数据型的方法，可以不断更新驾驶策略，即使线路发生变化，也能灵活应对。这种方法可以优化列车控制策略且不依赖之前关于列车动力学和列车速度曲线的知识，同时也可以灵活应对变化的铁路参数和运行时间。同时在理想驾驶策略的基础上，列车最大制动力、神经网络层数等也可能会对列车能耗造成一定影响。■