新型半潜式海上风力机基础水动力特性研究

魏东泽，阙小玲，付图南，周 阳，杜珈宇，王金涛

(1. 浙江海洋大学 海洋工程装备学院，浙江 舟山 316022; 2. 中国海洋大学 工程学院，山东 青岛 266100)

近些年来，海上风能开发进入了高速发展期。根据海洋可再生能源行动联盟预测，到2050年全球海上风电将达到1 400 GW，每年能减少超过30亿 吨的二氧化碳排放。近海风电场开发常与港口、渔业、航运等用海产生矛盾，因此学者们逐渐将目光转向深远海。研究表明，水深大于50 m时采用浮式基础的经济性将大幅提升[1]，其中半潜式基础因其适用水深范围广、机动性强等优点成为了研究重点。

近年来，学者们不断探索新型浮式海上风力机基础：如Bulder等[2]应用频域水动力方法探索一个三浮体基础的六个自由度运动RAOs特性。Wayman等[3-4]通过分析多个5 MW张力腿式风力机基础，开发了一套可以用来在频域内计算浮式风力机系统结构、水动力和空气动力耦合响应的程序，并研究了多种风力机基础在不同环境载荷下的动力响应。刘利琴等[5]研究了一种新型浮式基础的运动响应，在频域内计算了水动力参数和响应算子。唐友刚等[6]设计了一种适用新型半潜式基础，对该基础的稳性、运动和系泊张力进行了分析，结果表明黏性阻尼对运动影响显著。李溢涵[7]设计了一种Spar型风力机基础，在频域范围内研究了波浪入射角对基础运动响应的影响，结果证明波浪入射角对纵摇和纵荡自由度的运动响应影响较大。叶小嵘等[8]选择OC3-Hywind浮式基础风力机模型，考虑浮式基础随一阶波浪载荷周期运动，得到了风力机功率随风速的变化曲线。曹菡等[9]设计了一种半潜式风力机基础，并对其水动力性能进行了研究。相关的研究推动了半潜式海上风力机的研究，但是半潜式风力机垂荡性能差的问题仍未得到有效的解决。

针对半潜式风力机基础垂荡性能普遍较差的瓶颈问题，概念性地设计了一种新型半潜式海上风力机基础，旨在改善半潜式风力机的整体运动性能，并分析了基础在风浪联合作用下的水动力特性。

1 风力机系统结构及主要参数

半潜式风力机基础一般采用三立柱结构，上部风力机安装在其中一个立柱上(如图1)，这种结构型式不对称、重心高、浮心低、垂荡运动幅度大，风力机系统的整体稳性较差，对发电效率也有负面影响。

1.1 新型基础结构设计

针对常规三立柱基础的不足进行了改进，通过设置底部压载舱和水面浮箱的措施降低重心，提升浮心，提高系统的稳性和运动性能。总体布置如下：在基础底部设计一个半径为30 m的圆形压载舱，三个侧立柱设置在压载舱的边缘，呈等边三角形布置，三角形的边长为51 m。中心立柱设置在压载舱中心，侧立柱与中心立柱由水面浮箱相连，压载舱边缘等间距布置9个通孔(如图1所示)。

1.2 风力机及基础参数

本文所设计的半潜式风力机基础工作水深为200 米，风力机参数采用NREL公布的5 MW风力机数据，风力机及基础的参数如表1所示。风力机使用的是Pitch-Regulated Variable Speed(PRVS)控制系统来调节输出功率和结构负载。采用的5 MW风力涡轮机的切入风速为3 m/s，低于该风速产生的有效发电功率过小，切出风速为25 m/s，超出此风速则风力涡轮机必须关闭，以避免潜在的结构破坏。当风速小于额定风速11.4 m/s时，PRVS使发电机加速以保持额定功率，当风速在11.4 m/s至25 m/s之间时，发电机在PRVS的作用下保持定常扭矩，保证其发电量最大化。

表1 风机和基础主要参数

1.3 水动力分析模型

在SESAM的GeniE模块建立了水动力分析所需的面元模型和整体结构有限元模型并划分网格，风机在作业工况下叶片旋转所覆盖的面积为受风荷载作用的面积，如图2所示。

图2 面元模型和整体结构有限元模型Fig. 2 The panel model and integral structure finite element model

1.4 系泊系统布置

系泊系统采用由3组共9根系泊缆组成的悬链式系泊系统，每组内锚链夹角为10°，每两组锚链之间的夹角为120°，如图3所示，锚链的具体参数如表2所示。

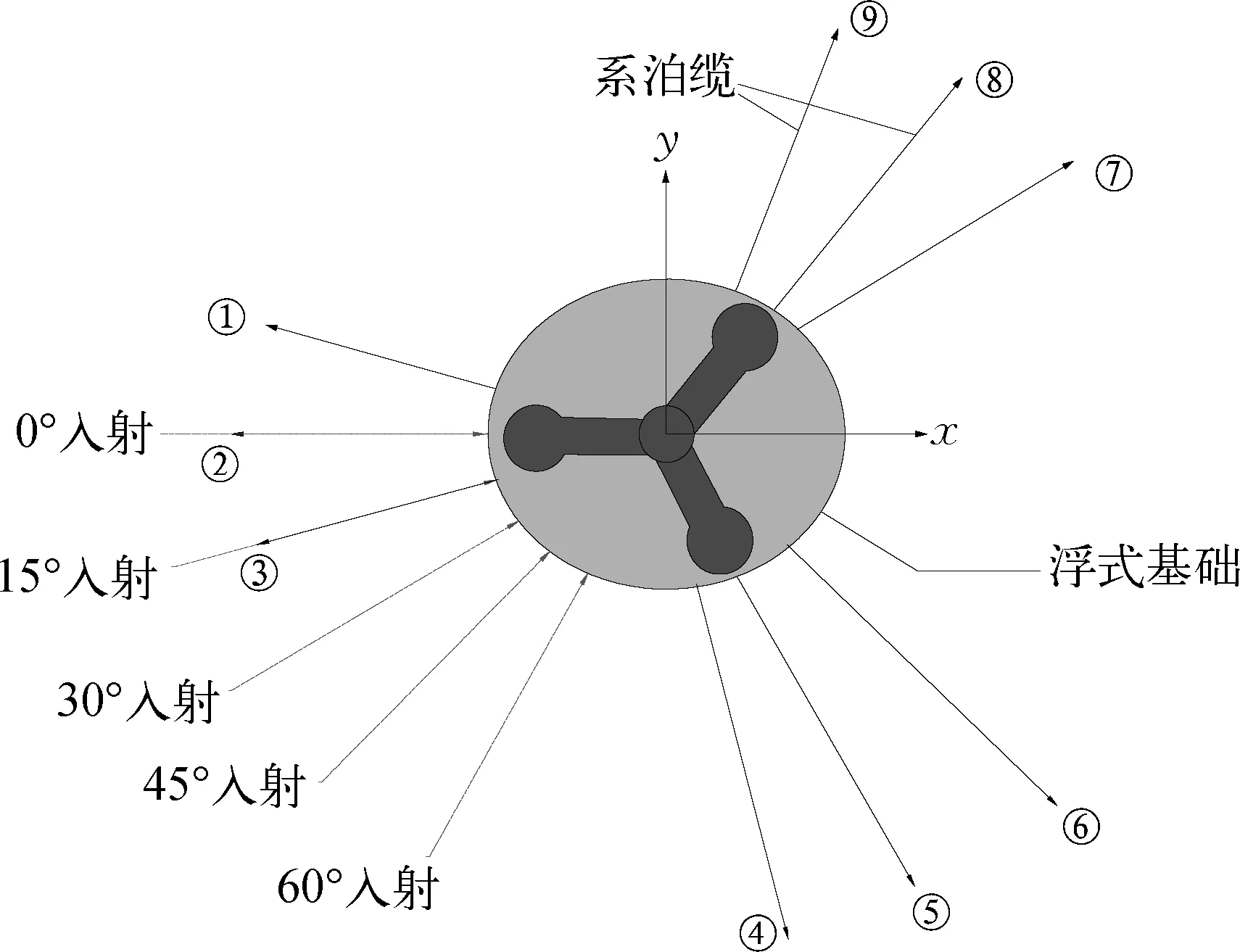
图3 系泊方式示意Fig. 3 Schematic diagram of mooring line arrangement and incident angle

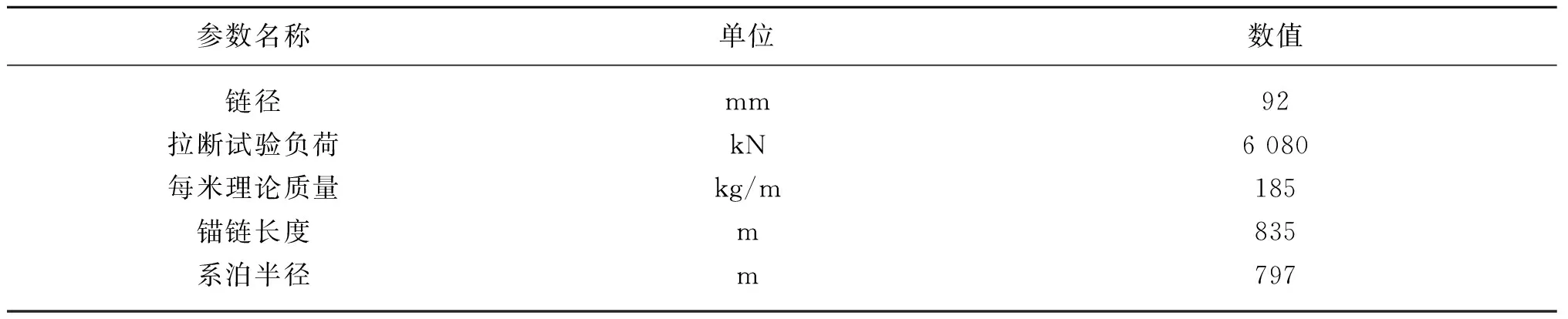
表2 锚链参数

2 计算理论

与海洋平台相比，海上风力机系统除水动力荷载以外，风荷载的影响同样显著，因此运动规律更为复杂。

2.1 风荷载

1) 叶片风荷载

风力机叶片上的荷载采用叶素—动量理论进行计算，考虑尾流作用时，轴向力和力矩可以表示为：

(1)

dM=4πρv∞(Ωr)b(1-a)r2dr

(2)

式中：ρ为空气密度；r为叶素展向长度；dr为叶素与轮觳之间的距离；Ωr为旋转的切向速度；a和b分别为轴向和切向诱导因子，可通过迭代法计算。

2) 基础风荷载

CCS规范对风力机基础风荷载如下：

F=0.613[∑(ChCsAi(a)ν2)]

(3)

式中：Ch为结构高度系数；Cs为结构形状系数；Ai(a)为投影面积；ν为相对风速。

3) 风倾力矩

CCS规范对风倾力矩的计算规定如下：

(4)

式中：Fi为受风构件所受风荷载；Zi为受风面积中心至水下侧向阻力中心的垂向距离。

2.2 波浪荷载

当波浪为简谐波时，半潜式风力机结构承受的波浪荷载可以表示为：

(5)

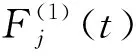
(6)

(7)

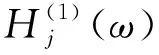
2.3 频域运动方程

根据势流理论，对于六自由度刚性浮体，其在水中的频域运动方程为：

(8)

式中：M为质量矩阵，Ma为附加质量矩阵，λm为阻尼系数矩阵，Cm为回复力系数矩阵，Fwm为入射波浪力。

2.4 时域运动方程

对于系泊的半潜式风机系统，其时域运动方程[10]可以表示为：

(9)

3 结果分析

3.1 自由衰减运动

分析新型风力机基础的自由衰减运动，得到其固有周期，并与常规基础进行比较，如表3所示。

表3 风机基础固有周期

设计海况波能集中周期区域为4～20 s，从表3可以看出，常规的半潜式风力机基础垂荡运动固有周期在波能集中区域范围内，容易引起结构的共振，垂荡性能较差。经改造的新型风机基础六自由度固有周期均不在波能集中区，特别是垂荡固有周期为35 s，远离了波能集中区，性能上优于其他两种基础型式。

3.2 黏性阻尼和势流阻尼

通过设置水面浮箱及圆形压载舱，增加了风力机系统的黏性阻尼，通过公式计算得到了等效黏性阻尼矩阵，将阻尼矩阵导入Wadam模块中计算幅频响应曲线。参考文献[1]提供了半潜式基础的临界阻尼β0计算公式：

(10)

式中：M0为结构质量或结构惯性矩，Mb为结构附加质量，Ci为结构静水回复力刚度。

研究表明[1]，半潜式基础的黏性阻尼可取临界阻尼的10%。表4给出了垂荡、横摇、纵摇运动的临界阻尼以及经计算得到的势流阻尼。

表4 半潜式风机基础临界阻尼和势流阻尼

从表4可知，垂荡、横摇和纵摇运动的黏性阻尼与对应的势流阻尼在同一数量级上，黏性阻尼的影响不可忽略，因此在后续水动力分析中考虑了黏性阻尼。

3.3 稳性分析

浮式风力机基础在复杂的海洋环境下，应具有足够的自存能力。为保证风机系统保持稳定的发电功率，对所设计的风力机基础进行了初稳性和大倾角稳性的校核。

3.3.1 初稳性分析

处于漂浮状态的半潜式风力机基础应具有足够的初稳性，以保证浮式基础有足够的回复力矩恢复到原平衡位置，不影响风机正常工作。在海洋平台的初稳性研究中，稳心高是衡量初稳性的重要指标。规范要求在设计海洋平台时最小初稳心高度应大于0.15 m。经Stability模块计算，基础的初稳心高为8.5 m，满足规范要求。

3.3.2 大倾角稳性分析

风力机上部风荷载较大，在校核大倾角稳性时，核算了额定风速11.4 m/s(工作工况)和50年一遇风速44.9 m/s(极端工况)时的风倾力矩。根据NMD[13]、CCG[14]等规范规定，半潜式基础计算得到的回复力矩曲线上，第二交点和进水角的较小者与曲线交点以下的面积与同一角度下风压倾覆力矩曲线以下的面积比应不小于1.3。利用HydroD中的完整稳性模块进行计算，结果如图4所示。

图4 工作海况和极端海况下完整稳性Fig. 4 Intact stability under working conditions and extreme conditions

此外，根据NMD[13]规定，当风力机处于正常工况时，回复力矩曲线与倾覆力矩曲线的第一交角在17°以内，而CCG[14]规定第一交角在15°以内，风力机可以保障发电效率。由图4曲线可以看出，工作海况下回复力矩曲线与倾覆力矩曲线的第一交角为7.5°，满足上述规定，且复原力矩和风倾力矩同倾角下的面积比可达5.95，完整稳性满足不小于1.3的规范要求。上述规范对于极端海况下的第一交角没有明确规定，经过计算，极端海况下复原力矩和风倾力矩同倾角下的面积比仍可达到2.58，足以保证风力机系统稳定不倾覆。

3.4 幅频运动响应分析

利用SESAM软件建立了风机系统频域响应水动力分析模型，为了使计算结果更加符合实际，计算中考虑了黏性阻尼的影响。选择波浪周期在3～42 s范围进行计算，以1 s为时间间隔，得到了基础在不同自由度运动方向(篇幅所限仅列举代表性的垂荡、横摇和纵摇三个运动)的一阶和二阶波浪力传递函数以及RAOs曲线图，如图5～7所示。

图5 一阶波浪力传递函数Fig. 5 Transfer function of first-order wave force

图6 二阶波浪力传递函数 Fig. 6 Transfer function of second-order wave force

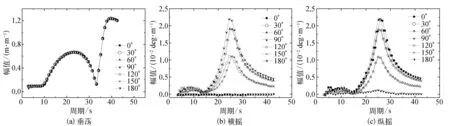
图7 运动RAOs Fig. 7 RAOs of motions

3.4.1 一阶波浪力传递函数

图5给出了不同波浪入射角下基础在垂荡、横摇和纵摇方向上的一阶波浪力传递函数。

从图5可以发现，三个运动方向一阶波浪力传递函数总体上呈现相似的变化规律，但入射角对垂荡基本没有影响，对横摇和艏摇传递函数的影响较大，这主要是由于新型基础对称的结构特点所决定的。一阶波浪力在5～15 s周期范围内达到了最大值，其中垂向波浪力最大可达8.297×106N/m，横摇方向上的波浪力矩最大值可达9.891×107N·m/m，纵摇波浪力矩的峰值可达1.037×108N·m/m。

3.4.2 二阶波浪力传递函数

通过对一阶波浪力的近场积分法计算，得到了不同运动自由度的二阶平均波浪力，如图6所示。

对比图5和图6各自由度一阶波浪力和二阶波浪力的数值可以发现，二阶波浪力均比相应的一阶波浪力小1～2个数量级。但是，二阶波浪力或波浪力矩均在波浪周期5～10 s内达到峰值，这一周期区间位于波能集中区，容易引起共振。因此，二阶波浪力在数值上虽然小于一阶波浪力，但其对运动响应和系泊力的影响不应忽略。同时，也可以看出二阶波浪力较一阶波浪力更为复杂，如横摇和纵摇方向上分别有若干个峰值周期，说明在较大波浪周期范围内结构均可能产生较大的运动幅值，需要引起重视。

3.4.3 运动RAOs

根据水动力分析计算，得出了基础垂荡、横摇和纵摇自由度RAOs，如图7所示。

从图7可见，垂荡方向上，不同波浪入射角运动曲线基本重合，说明波浪入射角对垂荡运动的影响不大。波浪周期在32 s以内的基础的垂荡运动幅值较小，在周期为38 s时的运动响应幅值达到峰值1.222，表明基础脱离了波浪能量集中区域。除垂荡以外，其他自由度的RAO在不同入射角条件下呈现不同的规律，但均避开了波能集中区，表明这种基础在频域范围内的水动力性能良好。纵摇方向上，不同入射角下基础的运动响应在8～12 s处均有一个次高峰，在25 s附近时均达到峰值，当周期大于25 s时，运动响应随波浪周期的增大反而减小，周期相同条件下，入射角为0°和180°时运动响应最大，90°时最小。横摇的RAOs特征与纵摇相似。

3.5 时域运动响应分析

利用SESAM-FAST-ORCAFLEX软件对半潜式风机系统进行风浪联合作用下的动力响应分析，计算时间为3 600 s，时间步长为0.05 s。由于结构的对称性，5种入射角设为：0°、15°、30°、45°和60°，风荷载和波浪荷载保持相同的入射方向(见图3)。设置了四种风浪工况组合，包括三种工作海况以及极端海况，以便分析风机系统在不同海况下的运动特征，风浪工况如表5所示。

表5 风浪工况组合

计算了不同的风浪入射角下，三种工作工况和极端工况各自由度运动响应的最大值情况，如图8所示。

图8 不同风浪入射角下运动响应最大值Fig. 8 Maximum value of motion response under different incident angles

从图8可知，在同一自由度下，风浪入射角对四种工况的运动响应都有一定影响，但程度有所不同。其中在极端工况下，风浪入射角的影响明显高于工作工况，尤其对横摇的影响最为显著。相比横摇而言，垂荡和纵摇受风浪入射角的影响较小。

为了全面分析风机基础的运动特性，对工作工况和极端工况下的运动响应进行统计分析，如表6所示。

从表6可知，总体上，风浪入射角对纵荡、横荡和艏摇极值影响较大，对垂荡、横摇和纵摇影响相对较小。四种工况下，风机系统的纵荡响应最大值均随风浪入射角的增大而减小，同一工况下纵荡响应最大值均发生在入射角为0°时，纵荡响应的平均值基本不受风浪入射角的影响。在三种工作工况下，纵荡最大值总体上随风速的增加逐渐增大，而纵荡响应平均值则随着风速的增加呈现先增大后减小的趋势，在工况2达到最大；横荡响应最大值和平均值均随风浪入射角的增大先增大后减小，当入射角为30°时达到最大；垂荡响应最大值、最小值和平均值受风浪入射角影响都很小；横摇运动响应均较小，随着风速的增大，响应最大值有小幅上升，但是在极端工况下，随着风速的大幅增大，横摇最大值并未明显增大，这主要是由于自存状态下叶片停止旋转，横向弯矩下降导致的。纵摇运动响应几乎不受风浪入射角的影响，纵摇响应最大值随风速的增大而增大。在三种工作工况下，纵摇均值先增大后减小，在额定工况下达到最大；艏摇运动响应最大值随入射角的增大呈先增大后减小的趋势，在入射角为30°时达到极值，在三种工作工况下，响应最大值随风速的增大而增大，但在极端工况下艏摇最大值有所下降。

表6 风机运动响应统计表

总体上，纵荡、横荡、垂荡和纵摇的最大值均出现在极端工况条件下，分别为13 m、3.4 m、3.6 m和7.9°，这可能是由于自存状态下，气动阻尼力减小，波浪频率接近结构共振频率导致运动响应较大。虽然这种情况下，仍可以满足规范规定的不大于水深8%和不大于15°的要求，但应高度重视极端工况下风机的安全。

3.6 系泊力分析

系泊系统是影响海上风力机运动响应和安全性的关键因素之一，对四种工况条件不同入射角度下系泊力情况进行了模拟计算，统计结果如表7所示。

表7 不同入射角下系泊力统计结果

从表7可知，同一工况下，系泊力总体上随入射角的增大而增大。系泊系统处于工作海况1和工作海况2时，4号锚链在风浪入射角为60°时受到的张力最大，分别为1 140 kN和1 280 kN；工作海况3时，5号锚链在风浪入射角为45°时受到的张力最高达到1 240 kN，对系泊系统的威胁程度最高。根据API规范[15]的规定，在使用动力方法进行分析时，系泊系统等效安全系数为1.67，上述工况的安全系数均符合规范要求。在极端海况时，风浪入射角为60°时，4号锚链承受的张力最高达到3 240 kN，对风机系统安全性最具威胁，此时锚链安全系数为1.88，CCS对于浮式风机系泊系统自存工况系泊最大张力的安全系数取值为1.8，因此仍满足规范要求。综上，波浪入射角度是影响系泊力的关键因素之一，在极端海况下，60°时最大张力是0°时最大张力的约1.5倍。此外，统计发现在风浪入射角45°和60°时系泊张力较大，容易对系泊安全产生威胁。

4 结 语

以所设计的新型半潜式海上风力机基础为对象，考虑了黏性阻尼和二阶波浪力的影响，通过频域和时域相结合的方法分析了基础在风浪联合作用下的水动力特性，得到以下结论：

1) 通过结构型式的改进有效提高了海上风力机系统的稳性，在工作工况和极端工况下均能满足稳性要求；

2) 通过圆盘型压载舱的设置，增加了垂荡附加质量和附加阻尼，克服了半潜式结构垂荡性能差的普遍性缺点，对比其他半潜式基础型式运动性能更为优越。

3) 在频域范围内，波浪入射角对垂荡的影响不大，但其他自由度RAOs在不同入射角条件下呈现不同的规律。垂荡、横摇和纵摇RAOs存在一个主峰值和次峰值，但峰值周期均远离波能集中区，表明不易引起共振。

4) 在时域范围内，风浪入射角对风机系统的动力响应和系泊力均有较大影响。总体上，风浪入射角对纵荡、横荡和艏摇极值影响较大，对垂荡、横摇和纵摇影响相对较小，纵荡、横荡、垂荡和纵摇的最大值均出现在极端工况条件下。同一工况下，系泊力总体上随入射角的增大而增大，在入射角为45°和60°时系泊张力达到最大值，容易对系泊安全产生威胁。相对于工作工况，极端工况下所受风荷载较小，但是系泊力更大，说明系泊力主要由波浪荷载主导，在系泊系统设计时应高度重视。