不同林龄马尾松人工林叶面积指数的测定

罗光浪，何世强，谭 伟，戚玉娇

（1.贵州大学 林学院，贵州 贵阳 550025；2.贵州省龙里林场，贵州 龙里 551200；3.贵州大学 林业信息工程研究中心，贵州 贵阳 550025；4.贵州省药用植物繁育与种植重点实验室，贵州 贵阳 550025）

叶面积指数（Leaf area index，LAI）可定义为单位水平地面面积上总叶面积的一半[1]，其为无量纲参数。LAI 常用于量化森林冠层结构特性[2]，并对森林植被的光合、呼吸、蒸腾、冠层截留降雨[3]等生理生态过程具有决定性作用[4-5]。因此，准确估测LAI 对评估森林生态系统生产力、林下植被更新以及生态系统对竞争、疾病及气候变化的响应极其重要[6-7]。

测定LAI 的方法有直接法和间接法。直接法经典、成熟且测量值相对精确，常用于校验间接法测定值，主要包括破坏性取样法、凋落物法和异速生长方程法等实测方法[8-9]。破坏性取样法是将研究样地内所有树木的叶片全部取下并测定总叶片的半表面积，再除以样地面积得到LAI[10]。但因该测量方法费时费力，且对植被冠层具有破坏性，被广泛应用于测定农田生态系统和冠幅较小树木的LAI，而难以用于测定高大森林冠层的LAI[10]。凋落物法是指在落叶季节通过收集凋落叶来计算LAI[11]，不具有破坏性，常用于测定落叶林或落叶季节LAI 的动态变化[12-13]，但无法获得生长季节的LAI。近年来，也有学者利用凋落物法结合展叶调查测定常绿林的LAI[14-15]。异速生长方程法是指在研究区内选择标准木，通过破坏性取样得到叶片生物量或叶面积与胸径或边材面积间的相关关系，从而推算出样地内的LAI[16]。该方法测量结果相对准确，与破坏性取样法相比避免了对森林的大面积破坏且工作量相对较小，但测量精度也受到林龄、密度、树种及立地条件等因素的影响[17-18]。

间接法方便快捷、不具破坏性，常用于监测不同森林类型LAI 的季节变化，如遥感法[19]和光学仪器法[20]。遥感法适用于大尺度范围内LAI的监测[21]。半球摄影法（Digital hemispherical photography,DHP）和LAI—2200 植物冠层分析法（LAI—2200）是目前广泛使用的光学仪器法[22-23]，但因自身局限性，需要进行合理校正以提高其测定精度。研究表明，木质部（指树干和树枝）、冠层水平上的集聚效应及簇内水平上的集聚效应是影响DHP 和LAI—2200 测定LAI 精度的主要误差源[24-25]。光学仪器因无法有效识别木质部而产生的误差通常采用木质比例（α）来量化[12]；因忽略冠层水平上的集聚效应而产生的误差用集聚指数（ΩE）来表示[26]；对于簇内集聚效应产生的误差则用针簇比（γE）进行分析[25]。相对于LAI—2200 法，DHP 还受曝光设置的影响[11]。此外，植被生长的非生物因子，如地形因子（海拔、坡度及坡向等）和土壤因子（含水率、容重及养分等）也是影响LAI 精度的重要因素[27]。

近年来，利用直接法和间接法测定森林LAI的对比分析报道较多。Jonckheere 等[16]利用异速生长方程法和光学仪器法（DHP 和LAI—2000）测定了欧洲赤松Pinus sylvestris林的LAI，结果表明DHP 和LAI—2000 测定值比异速生长方程法测定值分别平均低估55%和52%。Kalácska 等[28]在研究热带落叶林LAI 的季节变化时得出，LAI—2000 法比凋落物法测定值低估了17%～40%。此外，许多研究也对直接法和间接法测定森林LAI的回归关系进行了探讨。如曾小平等[29]采用CI-110 植物冠层分析仪测定了鹤山丘陵3 种人工林（荷木Schima superba、针叶林和马占相思Acacia mangium）的有效LAI，并构建了该方法与异速生长方程法测定值的回归方程，结果表明拟合度较高（荷木林：R2=0.86；针叶林：R2=0.82；马占相思林：R2=0.79）。Qi 等[12]利用凋落物法和DHP测定了小兴安岭阔叶红松Pinus koraiensis林7—11月LAI 的季节变化，得出两种方法测定LAI 呈显著的幂函数回归关系（R2=0.84）。然而，国内关于异速生长方程法和光学仪器法测定马尾松Pinus massoniana人工林LAI 关系的研究尚少。

马尾松人工林是我国南方森林生态系统主要人工林类型之一，广泛分布于亚热带区域。根据第八次全国森林资源清查结果，以马尾松为优势树种的森林面积为1 001 万hm2，是面积排位第5的优势树种，占全国森林资源总面积6.08%；蓄积量为5.91 亿m3，占全国森林总蓄积的4.00%，在木材生产、植被恢复和生态系统服务等方面均发挥着十分重要的作用。目前，针对马尾松林的研究主要集中在林分结构[30]、生长模型[31]、经营改造[32]、病虫害防治[33]、林下凋落物及土壤特性[34]等方面，鲜见对该林型LAI 精准测定方面的报道。本研究以贵州黔中地区幼龄林、中龄林、近熟林及成熟林马尾松人工林为研究对象，采用异速生长方程、DHP 和LAI—2200 法测定其LAI，分析不同方法测定值的差异，构建异速生长方程法与DHP 和LAI—2200 法测定LAI 值间的回归方程，为提高光学仪器法估测马尾松人工林LAI 的精度提供基础参数和科学依据。

1 研究地区与研究方法

1.1 研究地区概况

研究区域位于贵州省龙里县境内（107°01′～107°14′E，26°50′～26°56′N），地处苗岭山脉中段，乌江水系（长江流域）与红河水系（珠江流域）的支流分水岭，地形较为复杂，海拔在770～1 775 m 之间。研究区属于亚热带湿润季风气候，年均气温14.8℃，最冷月平均气温4.6℃，最热月平均气温23.6℃。年均降水量为1 100 mm，无霜期为283 d。调查样地内裸露岩石类型主要为砂岩和石灰岩，土壤主要为黄壤。马尾松人工林的林下灌木主要有白栎Quercus fabri、杜鹃Rhododendron simsii、粉枝莓Rubus biflorus等，草本植物主要包括蕨Pteridium aquilinum var.latiusculum和芒萁Dicranopteris pedata等。

1.2 研究方法

1.2.1 样地设置

在幼龄（8 a）、中龄（13 a）、近熟（22 a）及成熟（30 a）的马尾松人工林内，分别设置3 个20 m × 30 m 的临时样地，共计12 个。对样地内胸径≥2 cm 的马尾松进行每木检尺，记录树高、胸径、坐标等基本信息（表1）。

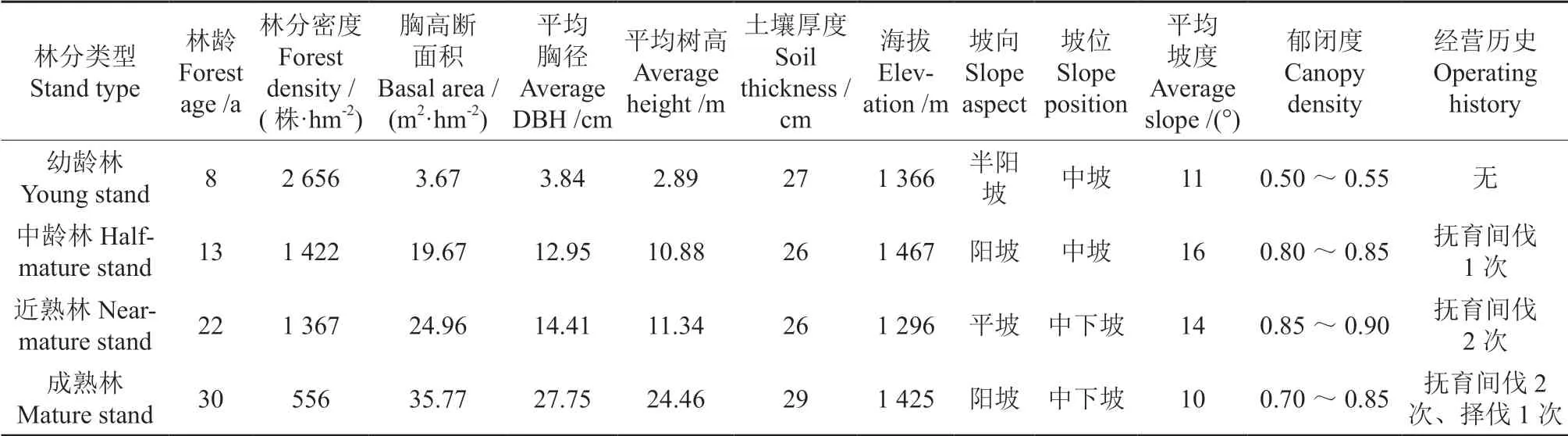
表1 不同林龄马尾松人工林样地基本概况Table 1 The basic characteristics of Pinus massonianaplantations at different ages

1.2.2 异速生长方程法

根据4 种林龄马尾松人工林每木检尺的胸径统计数据，将林层分为主林层、次林层和被压层。在各林龄3 个林层分别选取3 棵样树，即优势木、标准木及被压木各3 棵，4 种林龄合计36 棵，伐倒并测定全部针叶鲜重，同时采集大量针叶样枝带回实验室。马尾松针叶的形状近似椭圆柱体，针叶顶部形状是渐尖的，可忽略其表面积，采用体积替换法[25]测定针叶半表面积。具体测定方法为：首先找一个空间足够大装满水的容器，将针叶样枝完全放置水中，增加的重量即为针叶样枝的体积（V1）；其次，从针叶样枝上摘取针叶，测定针叶平均长度（l）和针数（n）；最后利用相同方法测定摘取针叶后样枝的体积（V2），针叶体积V=V1-V2。马尾松针叶半表面积计算公式如下：

式中：A为针叶半表面积，cm2；n为针叶数量；v为针叶体积，cm3；l为针叶平均长度，cm。

将测量完的针叶样本放置于65℃烘箱内烘干至恒质量后称质量（精确到0.001 g）。计算针叶比叶面积（Specific leaf area,SLA），计算公式如下：

式中：Si为林龄i的马尾松比叶面积，cm2/g；A为针叶i的半表面积，cm2；W为针叶i的干质量，g。

结合各林龄马尾松的SLA，得到各林龄马尾松单木的叶半表面积。在样地调查过程中，因胸径数据测量方便，且能保证较高精度，故将胸径作为自变量，叶半表面积作为因变量，建立各林龄马尾松人工林的异速生长方程。

1.2.3 光学仪器法

将12 个20 m × 30 m 的临时样地按10 m ×10 m 划分为72 个小样方。2016年8月，采用Winscanopy 2006 冠层分析仪（Regent,Instruments,Quebec,Canada）获取每个小样方的半球摄影图像。该冠层分析仪由数码相机（Canon EOS 6D）和180°鱼眼镜头组成。采集数据时将三脚架固定在离地面高1.3 m 处，摄像时使相机保持水平，并设置为自动曝光状态。为避免太阳光直射，选择阴天或日出日落前后进行拍摄。LAI—2200 植物冠层分析仪（LI-COR,Lincoln,USA）采集数据的时间、地点和距离地面高度与Winscanopy 2006 冠层分析仪相同，且确保光学感应探头保持水平。

光学仪器法主要根据穿透冠层的辐射获得林隙分数来计算LAI。在计算LAI 时，假设林冠内叶片处于随机分布状态，没有考虑冠层水平和针簇水平上的集聚效应，且忽略了除叶片外其他组分如树干、树枝等木质部分的影响，因此其估测值通常被认为是有效LAI（Effective LAI,Le）[35]。Le 由Miller 定律[36]推算得到，计算公式如下：

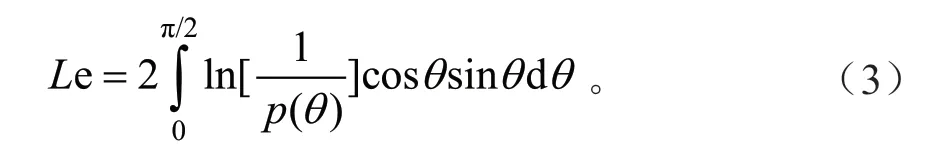
式中：θ为天顶角；P(θ)为天顶角θ的林隙分数。

为获得更准确的测定值，上式计算出的Le 仍需进一步校正[25]：

式中：Lc 为校正LAI；Le 为有效LAI；γE为针簇比（Needle-to-shoot area ratio）；ΩE为冠层水平集聚指数（Clumping index），基于林隙大小分布理论计算得到的[17]；α为木质比例（Woody-to-total area ratio）。α由以下公式计算得到：

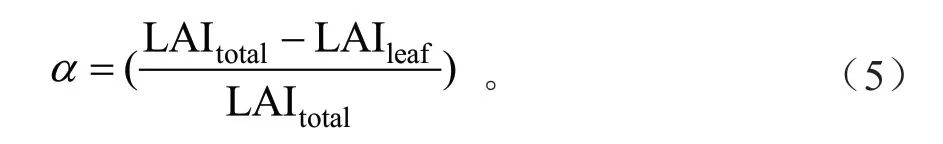
式中：LAItotal为DHP 软件处理半球摄影图像得到总的LAI（包括叶片和木质部分）[37]；LAIleaf为DHP 软件处理经由Photoshop 7.0 软件去除树干等木质部分后的图像得到的LAI[12]。

1.2.4 针簇比

将上述36 棵伐倒木的树冠分别按高、中和低3 个部位采集针叶样簇，每部分采集9 个，4 种林龄马尾松林共得到972 簇针叶样品，带回室内进行处理和分析。γE依据文献[25]的方法测定，计算公式如下：

式中：An为样簇上所有针叶表面积的一半（cm2）；As为样簇投影面积的一半（cm2）。

An采用体积替换法测定，As依据如下公式计算得到[25]：

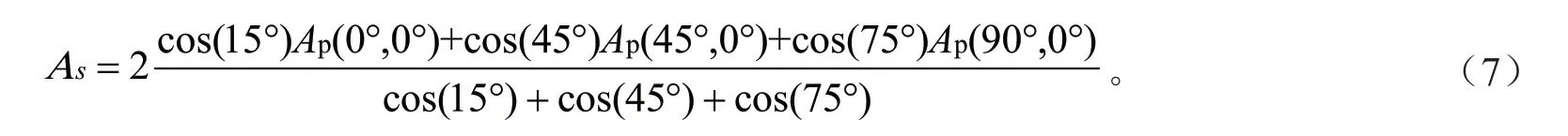
式中：Ap为样簇角度为0°、45°和90°的投影面积，cm2。

1.3 数据分析

利用DHP 配套软件计算半球摄影图像中30°～60°天顶角范围内的Le[38]，同时利用DHPTRACWin 软件[39]获取天顶角为40°～45°的冠层水平集聚指数（ΩE）。采用FV2200 软件提取LAI—2200 法测定的3～4 环范围内的Le。采用单因素方差分析（One-way ANOVA）和LSD（Least significant difference）多重比较法对不同林龄马尾松林的ΩE、γE及α进行差异显著性检验（α=0.05）。构建异速生长方程法及其与DHP、LAI—2200法测定LAI 的回归方程，并计算模型的决定系数（R2）、均方根误差（Root mean square error,RMSE）以及概率P值。统计分析采用SPSS 18.0软件完成。

2 结果与分析

2.1 异速生长方程

由图1 可知，4 种林龄马尾松样树的针叶半表面积与胸径均呈幂函数关系，且相关关系显著（P＜0.01）。幼龄林、中龄林、近熟林和成熟林异速生长方程的决定系数R2分别为0.83、0.88、0.80 和0.89，RMSE 分别为0.19、0.42、0.43 和0.33。

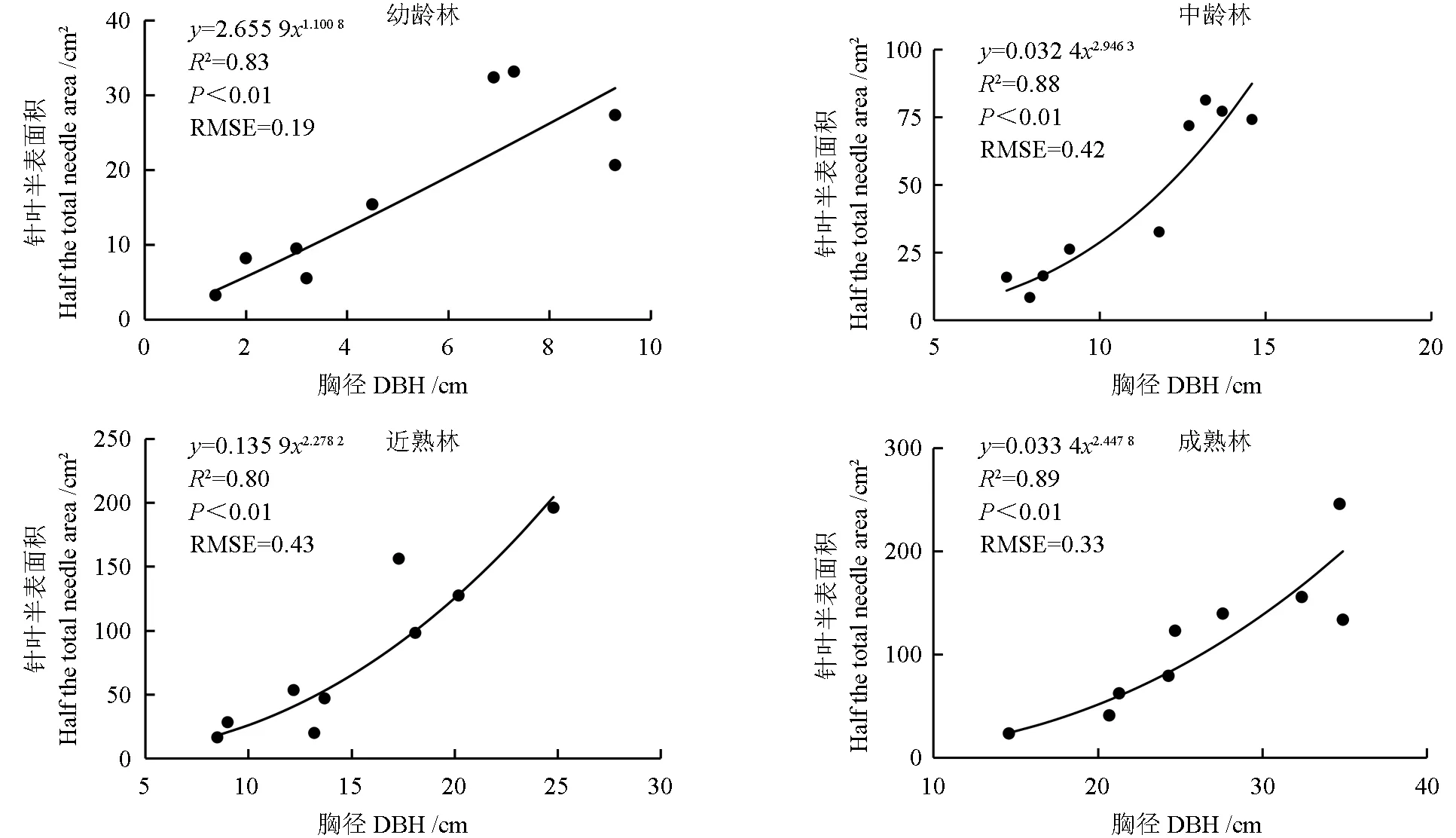
图1 不同林龄马尾松异速生长方程Fig.1 The allometric equations of Pinus massoniana at different ages

2.2 马尾松人工林的比叶面积

由表2 可知，不同林龄马尾松人工林的SLA存在差异，中龄林的最大，为106.53 cm2·g-1，幼龄林的最小，为73.12 cm2·g-1。

表2 马尾松人工林的比叶面积Table 2 Specific leaf area of Pinus massonianaplantations

2.3 光学仪器法的主要校正参数

木质比例变化范围为0.01～0.14，各林龄间存在显著差异，表现为幼龄林＜成熟林＜近熟林＜中龄林。幼龄林与其他3 种林龄的集聚指数存在显著差异，幼龄林的最小（0.79），成熟林的最大（0.91）。随着林龄的增大，针簇比呈显著增大趋势（图2）。

图2 光学仪器法测定马尾松人工林LAI 的主要校正参数Fig.2 Clumping index(ΩE),needle-to shoot area ratio(γE)and woody-to-total area ratio(α)of LAI of Pinus massoniana plantations determined by optical instruments

2.4 直接法和光学仪器法测定LAI 的比较

由表3 和图3 可知，各林龄异速生长方程法LAI 值大小依次为中龄林＞近熟林＞成熟林＞幼龄林。异速生长方程法测定值与DHP、异速生长方程法测定值与LAI—2200 测定的有效LAI 均存在显著差异（P＜0.05）。DHP 测定的幼龄林、中龄林、近熟林和成熟林的有效LAI 依次比异速生长方程法测定值低估56%、52%、47%和42%，LAI—2200 测定的有效LAI 依次低估49%、37%、39%和41%。LAI—2200 法的低估程度均小于DHP 法，表明未经过校正的LAI—2200 测定值精度高于DHP。经α、ΩE、和γE校正后，DHP 测定的幼龄林、中龄林、近熟林及成熟林LAI 比异速生长方程法测定值分别低估14%、31%、16%和3%，估测精度明显提高。而LAI—2200 测定值经α、ΩE、和γE校正后，各林龄的低估程度均小于10%，估测精度大幅度提升。校正后的DHP 和LAI—2200 测定值与异速生长方程法测定值在幼龄林、近熟林及成熟林中均不存在显著差异（P＜0.05）。

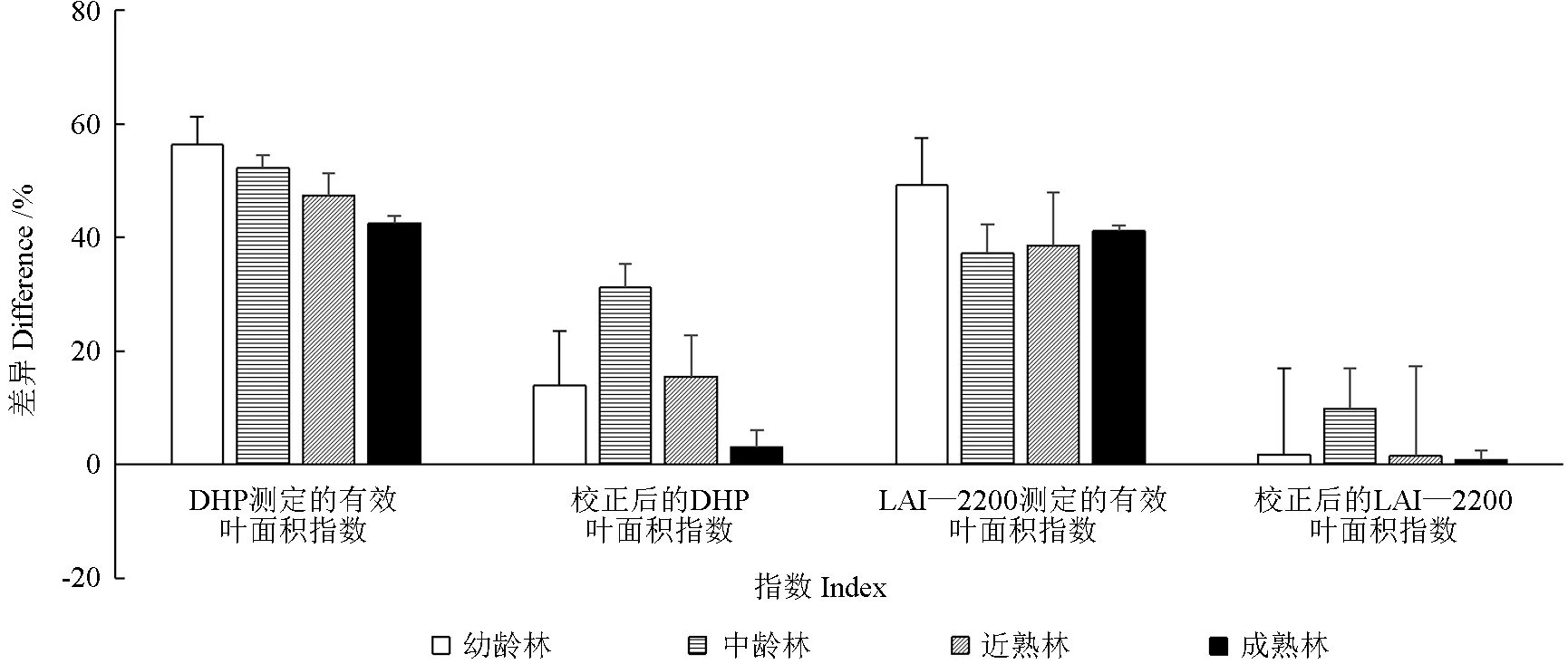
图3 不同林龄马尾松人工林异速生长方程法与光学仪器法（DHP 和LAI—2200）测定LAI 的差异Fig.3 The differences between allometric equations and optical methods in the determination of LAI of Pinus massoniana plantations at different ages(DHP and LAI-2200)

表3 不同林龄马尾松人工林异速生长方程法与光学仪器法（DHP 和LAI—2200）测定的LAI（平均值±标准差）†Table 3 LAI estimated by the allometric equations and optical methods(DHP and LAI-2200)of Pinus massoniana plantations at different ages(Mean±SD)

2.5 回归分析

异速生长方程法测定LAI与DHP以及与LAI—2200 测定的有效LAI 均呈显著回归关系（P＜0.01）（表4）。经过木质比例、集聚效应及针簇比校正后，DHP 和LAI—2200 测定值与异速生长方程法测定LAI 间的回归关系均增强，R2分别为由0.43 变为0.56，由0.65 变为0.70。结果表明木质部、冠层水平上的集聚效应及叶簇水平内的集聚效应能解释DHP 和LAI—2200 法测定LAI 时产生的偏差。

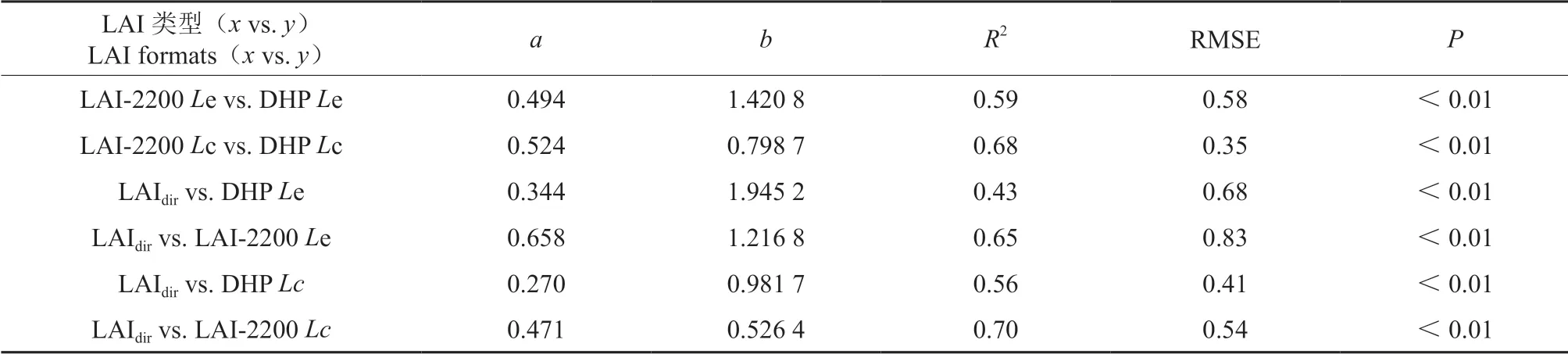
表4 光学仪器法（DHP 和LAI—2200）与异速生长方程法测定LAI 间的回归关系†Table 4 Regression equations between optical LAI(DHP and LAI—2200)and allometry

3 结论与讨论

采用异速生长方程法获取了4 种林龄马尾松林LAI，发现中龄林的LAI 最大，近熟林次之，幼龄林最小。这可能与林分密度、林分平均胸径、林分平均树高及胸高断面积的综合影响有关[40]。本研究对中龄林、近熟林及成熟林实施抚育间伐经营措施（表1），随着间伐强度的增强，林分密度减小，LAI 呈现逐渐减小的趋势，这与董莉莉等[41]的研究结果类似。各林龄马尾松针叶半表面积与胸径的回归关系显著（P＜0.01，R2＞0.80）。曾小平等[29]建立马占相思、杉木Cunninghamia lanceolata及荷木林总叶面积与胸径间的回归方程也具有较高的拟合度（R2＞0.89），Jonckheere 等[16]对欧洲赤松的研究也得到类似的结果。Gower 等[42]研究表明同一地区不同树种间和同一树种不同地域间的异速生长方程存在差异，且不适用于测定LAI 的季节动态。周明等[43]利用异速生长方程法和凋落物法测定了兴安落叶松人工林叶面积最大时期的LAI，并对比了两种测定值的差异，表明差异不显著，说明异速生长方程法虽受到地域、树种及林龄等的限制[17]，但只要合理运用，仍有较广泛的适用性。本研究未使用凋落物法，但构建的异速生长方程相对稳健，适合用于校正光学仪器法的测量值。当然，后续会继续开展凋落物法的研究，测定LAI 的季节动态并分析其与异速生长方程法测定LAI 的差异。

以异速生长方程法测定值为参考，评估DHP和LAI—2200 法测定的不同林龄马尾松林LAI，结果表明木质部和集聚效应是影响其精度的主要因素。光学仪器因无法有效辨别木质部和叶片，会导致计算LAI 时出现高估现象[25]，同时因忽略集聚效应而低估LAI[8]。本研究得出4 种林龄马尾松林的α均值为0.09，变化范围为0.01～0.14，主要与林龄差异有关。幼龄林处于生长初期，树枝及树干被新生叶片遮掩，从而减小了木质部对LAI 的贡献率，随着林龄增大，叶片凋落，被遮蔽的木质部逐渐暴露而导致α值增大。但α总体变化范围与其他林型相差不大，Deblonde 等[44]测定的多脂松Pinus resinosa林的α值在0.08～0.12之间，斑克松Pinus banksiana林的α值变化区间是0.10～0.33。此外，季节变化也是影响α值的重要因素，刘志理等[45]利用相同方法量化了阔叶红松林内α值随季节呈单峰型变化，范围为0.03～0.11。本研究未探讨季节是如何影响α值的，后续将开展相关研究。马尾松林冠层水平上的集聚指数ΩE均值为0.87，与其他森林类型的相关报道结果类似。如小兴安岭谷地云冷杉Abies nephrolepis林ΩE均值为0.90[46]，香脂冷杉Abies balsamea林和黑云杉Picea mariana林的ΩE均值分别为0.95 和0.91[38]。马尾松的针簇比γE均值为1.59，与Gower 等[47]报道美国赤松的γE值（1.50）接近，但小于红松的γE（1.73）[45]，主要因树种叶形态特征的差异，如马尾松和美国赤松针叶均为两针一簇，而红松为五针一簇。当然地域对γE值也有重要影响，Deblonde 等[44]测定的加拿大地区赤松的γE值约为美国的2 倍。

本研究中DHP 和LAI—2200 测定的有效LAI比异速生长方程法测定值分别低估了41%～56%和36%～49%。研究表明，光学仪器方法测量的LAI 普遍存在低估现象[38]，但不同林型低估程度不同。王宝琦等[48]采用DHP 测定红松人工林的有效LAI 比异速生长方程法-A 和异速生长方程法-B 平均低估70.18% 和81.69%。Küßner 等[18]曾报道挪威云杉Piceaspp.林的DHP 测定值比异速生长方程法低估了37%～82%。Mason 等[49]利用LAI—2000 法测定新西兰松树林的有效LAI 比异速生长方程法低估了30%～60%。相比实测法，光学仪器法能方便快捷获取LAI，因此为了能快速准确地获取LAI，通常需要对光学仪器法测定值进行校准。经α、ΩE、和γE校正后，DHP 测定精度提高到79%以上，LAI—2200 法的测定精度高于90%。本研究利用DHP 测定马尾松林LAI 时未采用最优曝光模式，是其测定精度低于LAI—2200 的主要原因。Zhang 等[50]研究表明DHP 在自动曝光状态下测定的Le 值比LAI—2000 低估16%～71%。为提高DHP 的测定精度，后续研究应更多关注曝光设置问题。

关于直接法与间接法测定LAI 间的回归关系已被广泛报道[20,51]。本研究中异速生长方程法与光学仪器法（DHP 和LAI—2200）测定马尾松人工林LAI 间存在显著的线性回归关系（P＜0.01），经误差源校正后，两者的回归关系明显提高，表明建立直接法与光学仪器法测定LAI 间的经验模型利于提高森林LAI 估计的精度。但直接法与光学仪器法构建回归方程的决定系数R2值不高，分析其原因，可能是因为利用光学仪器在每个样方内只测定一个点有关，为减少测量误差，通常是测定多个点取平均值。另外，DHP 法并未进行曝光设置的校正，也没有综合考虑如地形因子及土壤因子等对LAI 的影响。Naithani 等[52]研究表明随海拔的升高LAI 呈增大趋势，Bequet 等[7]研究表明地形因子可直接影响植物生长或间接影响土壤因素的分布从而影响LAI，后续将综合考虑上述因素并开展深入研究。