程序设计研究式教学方法与实现——以内部排序为例

孙光灵

（安徽建筑大学 电子与信息工程学院，安徽 合肥 230601）

程序设计中的排序是一项重要的教学内容，在数据处理与分析中占有重要地位。作为数据处理的一种重要操作，排序功能是将一个初始的数据序列，重新排列成一个按关键字有序的新序列[1-2]。排序操作有内外之分，分别称之为内部排序、外部排序。排序操作在程序设计中涵盖排序算法设计、循环结构程序设计、数组作为函数参数、递归程序设计等知识点。是一项综合多个知识要素的复合性教学内容。

1 目前的研究现状

许多研究者从不同角度进行了探索和研究，王德超[3]列出了常用排序算法的算法流程，并对几种算法进行了分析与比较，给出了部分代码，总结了相关的内容。孔峰[4]对AHP综合排序算法进行了分析，针对综合排序时不能保持各方案之间的独立性问题，对算法缺陷进行改进策略，取得了较好效果。张明亮[5]等针对少量记录排序的应用，对直接选择排序算法进行了挖掘，通过增加记忆功能，使算法性能得到明显提高。李胜华[6]等对直接选择排序算法研究，解决了算法不稳定性、对数据的不敏感性的缺陷，提出了快速稳定表排序算法。算法约定用静态链表存储待排数据，先创建有序链表，再根据链接信息将数据顺序存储。算法保证排序的稳定性，也降低了时间复杂度，并且保证了后续其他操作也同样具备顺序存储的优点。余晟隽[7]等总结了常用的分布式排序算法，对每种算法的执行流程、代价模型和适用场景进行了分析，并通过实验对分析结果进行了验证。王修君[8]等从经典快速排序算法的递推关系和数学期望两种分析方法作为切入点，多角度分析该经典问题平均比较次数，探索教学过程的有效方法。

尽管许多研究者从不同方面对排序的内容进行了分析和简述，但根据已有文献内容来看，研究者没有从算法实施效率的角度进行对比教学设计，有效完成教学工作。

文章总结教学研究成果，从研究的基准点出发，对内部排序的内容进行教学设计。以计算思维为导向，突出重点和要点，综合程序设计各知识点，进行对比式研究和教学，以获得最佳教学效果。

2 研究式教学设计

2.1 内部排序的内容和分类

计算科学中的内部排序指待排序数据记录存放于计算机随机存储器RAM中，在内存中所进行的排序过程；当排序的数据过于庞大，内存一次不能容纳全部数据，需要在排序过程中不断访问外部存储器。在排序过程中存在内存数据和外存数据不断交换的操作。外部排序比内部排序更加复杂，文章以内部排序为例进行分析和研究。内部排序包含交换排序、基数排序、选择排序、插入排序、归并排序。排序算法如图1所示。

图1 排序分类结构图

研究过程选择图1中常用的7种经典排序算法，包括直接插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序、归并排序。下面分别进行讨论。

2.2 算法设计

为表述简便，做如下约定：①待排初始序列为｛R（48），R（37），R（65），R（96），R（75），R（11），R（26），｝；②递增排序③序列中的“正序”序列指{R（11），R（26），R（37），R（48），R（48），R（65），R（75），R（96）}；④“逆序”序列指{R（96），R（75），R（65），R（48），R（48），R（37），R（26），R（11）}。

2.2.1 直接插入排序 直接插入排序是从数据序列中取一个新的数据作为待排数据，将这个新数据插入到已排序好的有序表中，得到一个新的有序表，新有序表的长度增加1。排序过程如表1所示。

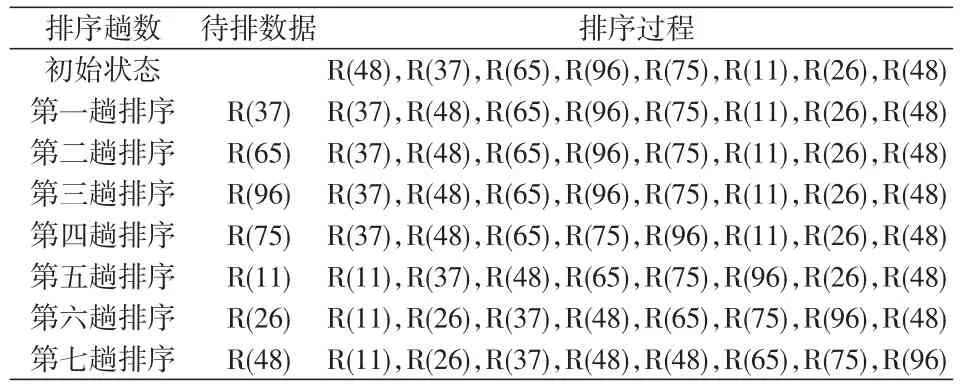
表1 直接插入排序表

直接插入排序所需要空间较少，仅需要一个数据的交换空间。具体操作是比较两数大小，对比较结果进行判断，以便决定是否对数据进行移动和插入操作。当待排数据为“正序”序列列时，所需比较次数和移动次数最小，比较为n-1次，数据移动2*（n-1）次。当待排数据为“逆序”序列时，所需比较和移动次数最大，分别是（n+2）*（n-1）/2和（n+4）*（n-1）/2。

2.2.2 希尔排序 希尔排序的主导思想是先将待排序列划分成为若干子序列，然后对对个子序列进行插入排序。当所有子序列中数据“基本有序”时，再对全体数据进行一次直接插入排序。算法如表2所示。

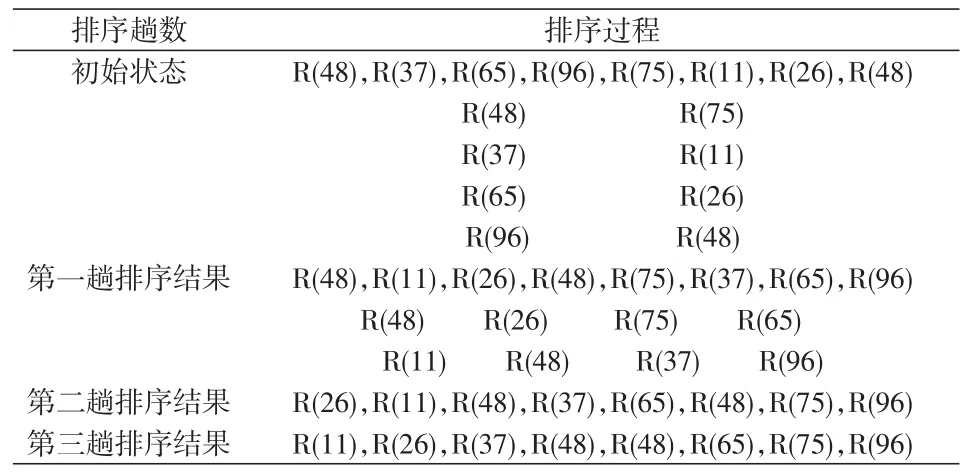
表2 希尔排序表

希尔排序的性能较为复杂，因为排序算法所需时间复杂度是“增量”序列的函数，而增量序列是根据排序的策略而变化。当前尚不明确最优的增量序列函数是否存在，以及如何推演。有研究者经过大量的实验以后，谨慎的指出，当增量序列取函数d[k]=2t-k+1-1时，希尔排序的时间复杂度为O（n3/2），式中t为排序趟数，取值范围（1≤t≤k≤[log2（n+1）]）。

2.2.3 冒泡排序 冒泡排序是借助“交换”进行排序的方法，算法采用相邻两数进行两两比较的办法，若为相比较两数逆序则进行交换操作。如表3所示。

表3 冒泡排序表

由上表中数据移动过程，可对冒泡排序效率的进行分析。当初始序列为“正序”序列，算法进行一趟排序即完成排序过程，没有数据的移动，排序过程对数据比较n-1次；如果初始序列为“逆序”序列，则需要进行n-1趟排序，比较次数为n*（n-1）/2次，数据移动也同步等量进行，所需时间复杂度为O（n2）。

2.2.4 快速排序 冒泡排序中不断进行相邻两的两两比较，效率较低，为减少比较次数，需要对冒泡排序的方法进行改进，形成快速排序算法。该方法的主导思想是，通过一趟排序将待排数据划分两组。其中一个组的数据均比另一组的数据小，称为快速排序的一次划分。快速排序过程如表4所示。

表4 快速排序表

就平时间来看，快速排序为Tavg（n）=k*n*ln n，其中n为数据总个数，n个数等待快速排序。k为常数，经验证明，在所有同数量级的先进的排序方法中，快速排序的常数因子k最小。因此，有研究者认为，快速排序是较好的方法这一，快速排序的时间消耗需要在实验中得到检验。

2.2.5 简单选择排序 简单选择排序过程比较容易理解，每趟排序时，确定待排数据，假定下标为i，对下标区间为[i+1，n-1]内数据进行比较，选出最小的数据，与下标i（1≤i≤n）的数据相交换。如表5所示。

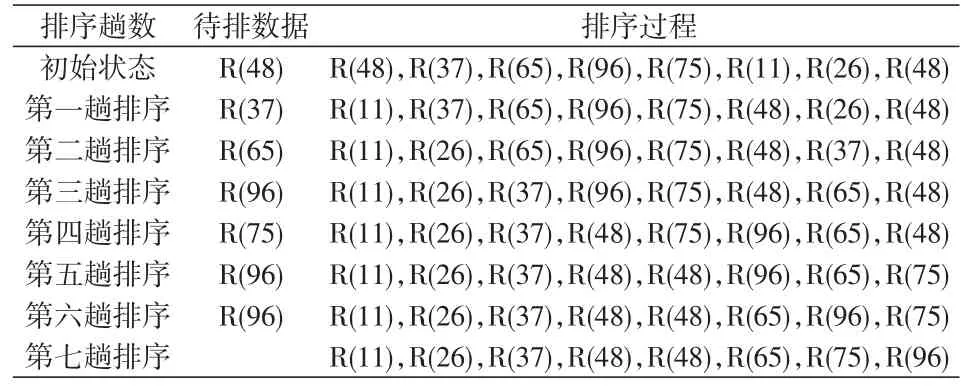
表5 简单选择排序表

简单选择排序算法运行过程中，可以估算出所需要移动的数据次数，待排数据为“正序”时，移动次数为0；为“逆序”时，数据移动数量最大，为3*（n-1）次。排序算法中数据的比较次数不受初始状态影响，次数均为n*（n-1）/2。简单选择排序算法总时间复杂度为O（n2）。

2.2.6 堆排序 堆排序是一种建立在完全二叉树思想上的排序方法，先把待排数据放在一维数组中，然后把初始数据构造成一个完全二叉树的大根堆[1]（每个结点大于其所有子结点，此时数组第一个元素最大。），再把堆顶（数组第一个元素）和数组最后一个元素互换，这样就把最大值放到了数组最右边。数组长度n-1，对剩余的（n-1）个元素再构造完全二叉树，形成新的堆，把剩余数据的最大值放到堆顶，输出堆顶（与剩余末排序数组最后面一个元素互换）。依此类推，直到最一个数据排序完成。如表6所示。

表6 堆排序表

堆排序在数据总量n较小时，效果并不明显；当n较大时，总体效果良好。对深度为k的堆，建堆过程中的比较次数不超过2*（k-1）次。一个含有n个元素，深度为h的堆，总共比较次数最大值为4*n。在最坏情况下，堆排序的时间复杂度为O（nlogn），需要的交换空间为O（1）。

2.2.7 归并排序 归并排序是把n个数据的初始序列分别作为n个长度为1的子序列，然后两两归并，得到[n/2]个长度为2的有序子序列（如果n为奇数，则存在1个长度为1的子序列）；再两两归并，直到最后得到一个长度为n的有序序列为止。又称2-路归并排序。如表7所示。

表7 2-路归并排序表

在归并排序算法中，排序趟数为[log2n]，时间复杂度为O（nlog2n）

所选排序算法性能比较如表8所示。

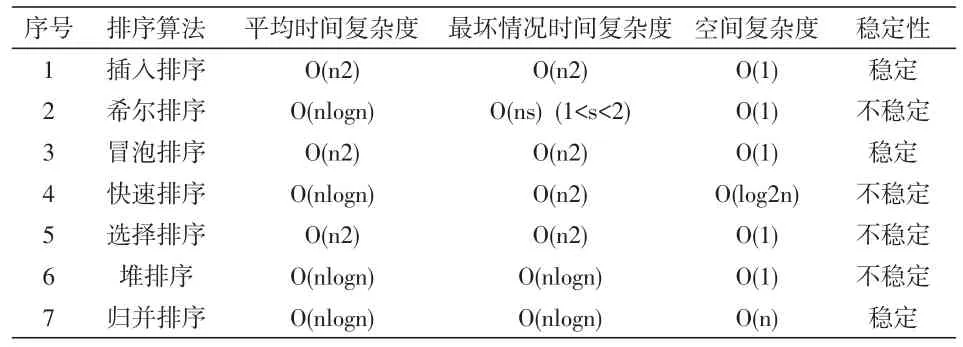
表8 排序算法性能比较

3 实验设计与分析

3.1 实验方案

本实验首先产生20000个大小为0-10000的随机整数，然后获取排序开始时间。再对七种排序算法分别进行排序，然后获取排序结束时间。时间相减得到时间差，再归一化处理，统一时间单位为秒。如图2所示。

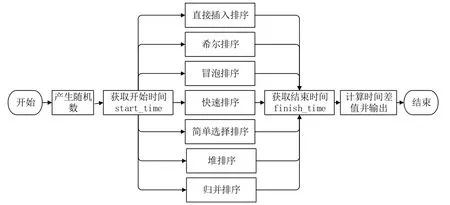
图2 实验方案图

3.2 实验数据及分析

实验在个人电脑中实施，电脑配置为Intel Core（TM）i5-4210M，8G内存，64位win8.1操作系统。实验采用C语言编程，在DEV-C编程工具中实现。经过程序运行10次，所得各算法所需时间如表9所示。

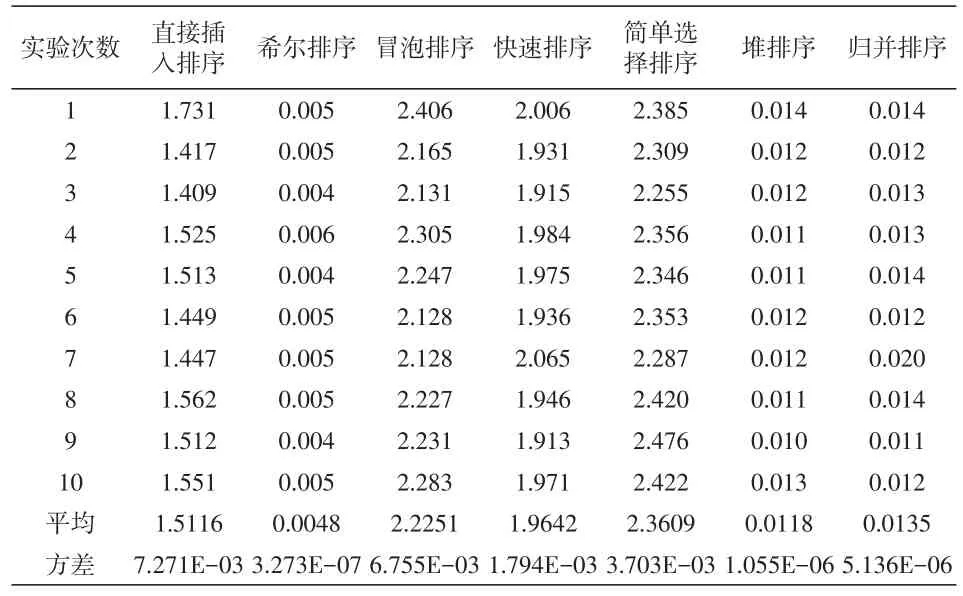
表9 排序算法消耗时间表（单位：s）

对上表中的数据，根据10次实验所得结果，绘制折线图如图3所示。

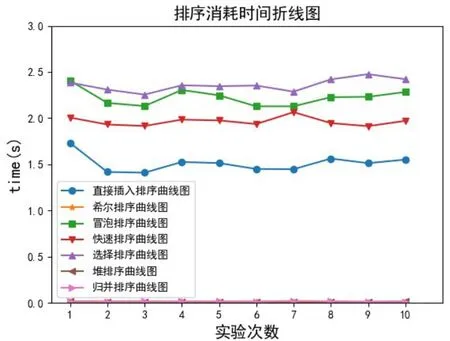
图3 七种排序花费时间折线斩图

由图3可以清楚地看出，简单选择排序、冒泡排序、快速排序、直接插入排序折线图在X轴上方，这四种排序方法相比较，直接插入排序所需时间较少，而简单选择排序花费时间最多。而希尔排序、堆排序、归并排序，相互交叠在一起，曲线接近X轴，表明这三种排序算法在时间方面有较好的性能。对表9中实验数据进行进一步计算，得到各算法消耗时间的均值和方差。由均值和方差数据可以看出，对1-10000以内的随机整数排序，希尔排序方差最小，运行最稳定；而直接插入排序方差最大，实验中达到7.271E-03秒，是希尔排序的22215倍，受排序初始数据的影响较大。

3.3 实验讨论

在实际工作中如何正确的选择排序算法是数据处理过程中的重要环节。由于排序算法的性能分析是一个复杂而困难的问题，所以需要对各算法进行实验仿真。前文中介绍了常用内排算法，从时间复杂度、空间复杂度及算法稳定性方面作了比较分析，指出了各算法的优势和不足之处。设计实验过程，用C语言编程实现这些算法，得到各算法所耗时间的数据。

受文章篇幅限制，实验过程中没有进行不同数量级的数据对比实验，即取 106、108、1010或更大范围的数据进行验证实验，分析不同范围的数据对算法性能的影响。在以后的工作中，会进一步分析、探索和验证。

4 总结

排序算法的教学是程序设计中的一个重要方面，也是比较困难的方面之一。通过研究式的分析，对比式的教学，可以让学习者比较全面的了解内部排序的状况、优劣和各项性能指标。在实际运用中能更好的选择合适的排序算法经通过几届的教学实验，学生在程序设计竞赛，建模比赛均取得的较好的效果。