大跨径桥墩对河道流态影响的数值模拟分析

于 浩，尚 华，孙维民

（1.水发规划设计有限公司，山东 济南 250000；2.山东大禹水务建设集团有限公司，山东 济南 250000）

目前山东省内跨河大桥的桥跨布置大多采用跨径为32 m的“经济型”桥墩布置，大跨径桥墩布置实际应用较少，相应研究更是匮乏，判断依据相对薄弱。本文以鲁南高铁跨沂河特大桥为例，应用数学模型模拟探寻不同跨径、不同角度桥墩布置对河道防洪影响程度及规律，为大跨径跨河桥墩布置提供理论参考。

沂河为天然山洪河道，桥址所在处较为顺直，河床比1/2 500，堤间距1 275 m，左边滩宽182 m，右边滩宽74 m，主槽宽1 019 m。桥址处沂河防洪标准为20年一遇。

1 平面二维水流数学模型的建立

考虑到河道水动力主要受上游河道下泄径流影响，因此本文采用工程附近局部二维水流数学模型的方法研究。工程所在河道为边界曲折、地形复杂的天然河道，要模拟此种复杂河道，可通过曲线坐标变换方法。

1.1 基本方程

在笛卡尔坐标系下，根据静压和势流假定，沿垂向平均的二维水流基本方程如下：

连续方程：

动量方程：

式中：ζ为自由水面高程，m；u、v为流速平均值，m/s；h为水深，m；f为柯氏系数，f＝2ωsinφ，ω为地球自转角速度，φ为当地经纬度；g为重力加速度；τsx、τsy分别是水面风切应力在x、y方向上的分量，τbx、τby分别是底部摩擦力在x、y方向上的分量，ρa为空气密度；ρw为水的密度；εx、εv为x、y方向紊动粘滞系数，m2/s。

1.2 定解条件

1）初始条件：

2）边界条件：

闭边界：

开边界：

式中：ζa、ua、va为已知的水位及x、y方向流速。

1.3 边界条件

20年一遇洪水时，上游控制边界为设计最大洪峰流量10 000 m3/s；下游控制边界为设计洪水位79.72 m。

1.4 计算网格

以该地区2015年实测地形图为基准，选取桥址上下游各2.5 km河段为计算范围，桥墩附近网格局部加密，网格尺寸0.5 m2，二维模型网格划分见图1。

图1 平面二维模型网格和桥墩布置局部网格示意图

1.5 计算参数

在二维水流模型中，上游进口断面沿用河道设计洪水分析成果，下游出口断面采用河道水面线计算设计水位。糙率参数采用河道治理成果，其中主槽0.034，滩地0.065。

2 桥墩布置对河道防洪影响

在20年一遇工况下，选取相同角度（0°）不同跨径的4组方案，见表1。对4组方案分别在桥墩与水流夹角4°、8°条件下模拟。

表1 不同桥墩布置方案

2.1 不同跨径桥墩对河道防洪影响

分别计算方案1~方案4最大雍水高度及流速增加值，见图2。

由图2可见，随着阻水比的减小，桥前最大雍水高度逐渐减小，且桥墩两侧局部流速增加逐渐减小，说明兴建桥梁对原河道影响程度逐步降低。

图2 不同跨径下最大雍水高度与流速增加值

2.2 不同角度桥墩对河道防洪影响

方案1~方案4在不同角度下的阻水比见图3。由图3可见，随桥墩轴线与河道中泓线夹角度数逐渐增大，其阻水比随之增大。但当角度过大时，会使得阻水比过高，如方案2在角度为4°时，阻水比为8.03%；方案3在角度为8°时，阻水比为8.07%，均超过规范推荐最大值8%。

图3 不同角度下阻水比与雍水峰值

进一步研究各角度下河道防洪影响程度，计算结果如图4。由图4可见，随着角度增大，阻水比逐渐增加，河道雍水高度在不断增大且两侧局部流速也在增大，这是因为水流流向在与桥墩轴线存在夹角时，会在桥墩上游侧产生绕流，形成局部漩涡，随着夹角的增大，绕流程度也在不断扩大。绕流对流速的影响随着角度的增大而不断增大，可以预见，随着角度的继续增大，这种影响会逐渐达到峰值，而后随之减小。

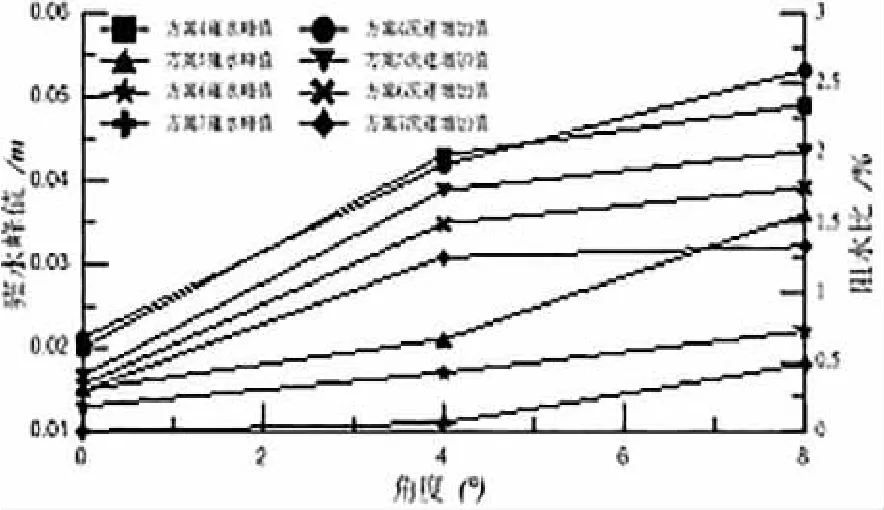
图4 不同角度下最大雍水高度与流速增加值

3 结论

1）随着跨径的增大，桥梁阻水比逐渐减小，建桥后最大雍水高度和桥墩两侧局部流速增加值逐渐减小。

2）随着桥墩轴线与河道中泓线夹角增大，阻水比逐渐增大，建桥后最大雍水高度和桥墩两侧局部流速增加值逐渐增大，即对河道防洪影响逐渐增大。

3）实际方案应考虑建桥的经济性和施工工期的可行性，结合桥墩布置对河道行洪影响程度综合分析，确定最佳方案。