物流业与国民经济三次产业间增长关系研究——基于我国1952～2020年统计数据

秦 愚 陈珍珠

（郑州大学管理工程学院，郑州 450001）

引 言

物流业是国民经济的重要组成部分，物流业的特殊性在于其与其他国民经济①组成部分间存在很强的互动。物流业发展促进三次产业发展，三次产业发展带动物流业发展。从1952～2020年，第一产业增加值从342.9亿元增长到77754.1亿元，复合增长率为8.3%；第二产业增加值从141.1亿元增长到384255.3亿元，复合增长率为12.3%；第三产业增加值从195.1亿元增长到553976.8亿元，复合增长率为12.4%；交通运输、仓储和邮政业增加值从29亿元增长到41561.7亿元，复合增长率为11.3%。不同类型的增加值数据都存在时间趋势，很容易掩盖它们之间的增长关系，进而掩盖国民经济运行机制。

研究物流业与三次产业间增长关系，有利于我们更加了解经济发展的内在规律，进而合理配置资源，优化产业结构，提高生产效率，实现我国经济的高质量发展。在提倡经济协调发展及物流行业降本增效的背景下，对物流业与第一、二、三产业间增长关系的研究显得尤为迫切。

1 文献综述

学者们对物流业与国民经济间关系进行了大量研究，相关文献可以从区域范围、研究方法、长期关系、短期关系等方面归纳。

1.1 区域范围

现有研究的区域范围可以分为全国层面、东、中、西部层面和省域层面。在全国层面，刘俊华等［1］研究指出，增加物流基础设施投资可以促进经济增长，且物流基础建设与经济增长之间具有长期稳定的均衡关系。在东、中和西部层面，聂正彦和李帅［2］研究指出，不同区域内物流业对中国经济增长均有显著的正向影响，但是不同区域的影响存在明显差异，东部物流业的经济增长效应最弱，中部次之，西部最强。王新玮［3］研究指出，物流基础设施对区域经济发展在每个时期均存在正向的空间溢出效应。在省域层面，王建林等［4］研究指出甘肃省国民经济的增长对物流产业的发展具有推动作用，两者之间相互协调。李绩才和吴坚［5］对浙江省现代物流与经济增长间的互动关系进行了实证分析，指出经济的快速发展优先促进了物流业发展，但物流业对经济发展的推动作用不显著。范林榜［6］利用1978～2010年的相关年度数据，对四川省和江苏省的物流和经济增长关系进行了实证比较分析，发现两地区的物流发展与经济增长均存在协整关系。唐建荣等［7］研究指出，中国省域物流业发展相关性和差异性并存。本文的研究范围定位在全国层面。

1.2 研究方法

学者们采取不同的研究方法对物流业与经济增长的关系进行了研究分析。其中，黄先军和李亦亮［8］基于灰色关联模型实证分析了安徽省物流业与其他产业之间的联动关系，结果表明安徽省物流业与其他产业的联动效应显著，物流业在产业体系中的地位日渐提高，具备成为主导产业的素质。李丽［9］基于协同学理论，验证了我国流通业与国民经济的协同关系，通过设计协同度评价模型，对两者之间的协同演进的一般规律进行了分析，结果表明我国流通产业对国民经济平稳运行的推进效应大于抑制效应。此外，张建军和赵启兰［10］采用协整分析、误差修正模型等方法重点研究我国农业物流与农业经济发展的互动关系，研究表明农业物流发展水平对农业经济发展水平具有显著的正向影响，农业物流是农业经济发展水平的格兰杰原因，农业物流发展水平短期波动对农业经济发展水平的影响较小，长期波动对农业经济发展水平影响较大。侯冠平和刘静暖［11］运用耦合度研究，指出三大产业与物流业之间是一个相辅相成的耦合系统，三大产业的不平衡性对物流业影响不尽相同。陈治国等［12］研究结果表明，全国物流业综合发展水平与国民经济综合发展水平间耦合关系与互动效应较好，但两者的耦合协调关系仍未步入协调状态。本文运用VAR模型及VECM模型对物流业与国民经济三次产业间的增长关系进行实证分析。

1.3 长期关系

王建林等［4］研究指出，甘肃省物流产业与国民经济之间存在协整关系。范林榜［6］指出四川省和江苏省的物流发展与经济增长均存在协整关系。刘俊华等［1］研究指出物流基础建设与经济增长之间具有长期稳定的均衡关系。吴继贵和叶阿忠［13］研究指出加强对物流业的投入对我国经济效率提升具有一定的促进作用，但是不同阶段的影响程度也有所差异。Tong和Yu［14］研究分析了交通运输与经济增长之间的协整关系，研究指出货物运输与经济增长之间存在长期均衡关系。以往研究的时间范围大都在改革开放后的30多年内，本文选取时间跨度更大的时间序列数据，即1952～2020年的统计数据，精准量化物流业与国民经济三次产业间的长期关系。

1.4 短期关系

现有研究中短期关系往往通过格兰杰因果关系揭示。赵立波［15］研究指出，经济增长是促进物流发展的根本动力，没有经济的快速发展，物流产业的发展就无从谈起。甘信华和刘峰［16］指出物流业与第一产业、第二产业存在单向因果关系，与第三产业存在双向因果关系。范林榜［6］研究分析得出四川省物流发展是经济增长的单向格兰杰原因，而江苏省经济发展是物流发展的单向格兰杰原因。吴继贵和叶阿忠［13］研究指出，物流业与经济增长二者之间并非完全双向互动的关系，即物流规模的增加能够促进经济的增长，但是经济的增长却不能反作用于物流规模的增长。Kuzu和Önder［17］研究指出经济增长是物流业的单向格兰杰原因。Tong和Yu［14］研究分析了交通运输与经济增长之间的因果关系，研究指出中西部欠发达地区货物运输与经济增长之间存在双向格兰杰因果关系。陈治国等［18］研究表明，无论是在价值层面还是在实物层面衡量的物流业对三大产业均有显著的促进效应。本文利用VAR模型探究物流业与其他国民经济三次产业之间的格兰杰因果关系。

本文基于1952～2020年我国年度统计数据，拟利用VAR模型和VECM模型，选择物流业及三次产业的年度增长率数据，分别从短期和长期两个角度对物流业和三次产业间增长关系进行实证研究［19，20］。

2 各变量数据选取及检验

2.1 变量选取及数据收集

本文选用拟选择以下指标。

（1）物流业增长指标（logistics）。衡量物流业增长的指标有许多，但其侧重面不同，考虑到交通、仓储及通信业是现代物流业的主要部分，所以本文选择交通运输、仓储和邮政业增加值作为衡量物流业增长的指标。

（2）第一产业增长指标（vd1）。考虑第一产业发展衡量指标的代表性及可获得性，本文选取第一产业各年的增加值。

（3）第二产业增长指标（vd2）。考虑指标反映第二产业的有效性，及数据的可获得性，本文选取第二产业增加值作为第二产业增长的衡量指标。

（4）第三产业增长指标（vd3d）。考虑所选指标的代表性，以及变量数据的可获得性，本文选取第三产业增加值作为衡量第三产业增长的指标。同时，因为物流行业属于第三产业，将从第三产业增加值中剔除交通运输、仓储和邮政业增加值。

本文所涉及的数据来自于 《中国统计年鉴》、国家统计局官网。对各变量数据进行自然对数标准化处理，得到llogistics、lvd1、lvd2、lvd3d。对数变换之后，回归方程中自变量的系数表示自变量与因变量间的变化弹性。

2.2 相关性分析

本文通过Stata16.0对数据进行分析处理，各变量取对数后的变化如图1所示。图中纵轴表示各变量的对数值，因为对数函数在其定义域内是单调递增函数，因此取对数不会改变原始数据的相对关系，从图中可以看到各变量逐年递增的变化趋势。取各对数变量的一阶差分，并画图得到图2，其中纵轴表示各变量的增长率。根据相关性分析结果，如表1所示。可知第一、二、三产业发展与物流业发展两两之间的相关系数最小为0.994，最高达到0.997，表明各变量两两之间存在着高度相关性。

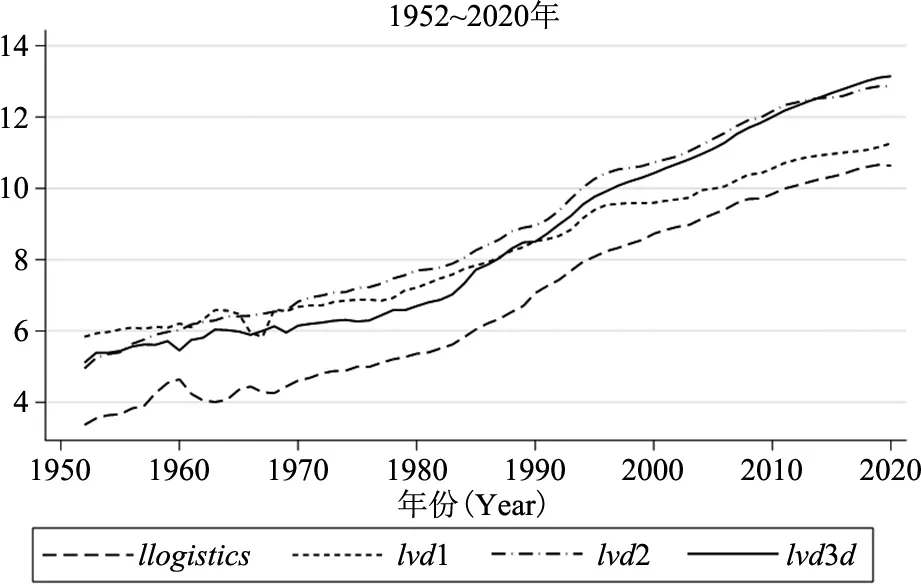
图1 各变量取对数后的变化

图2 各变量取对数差分后的变化

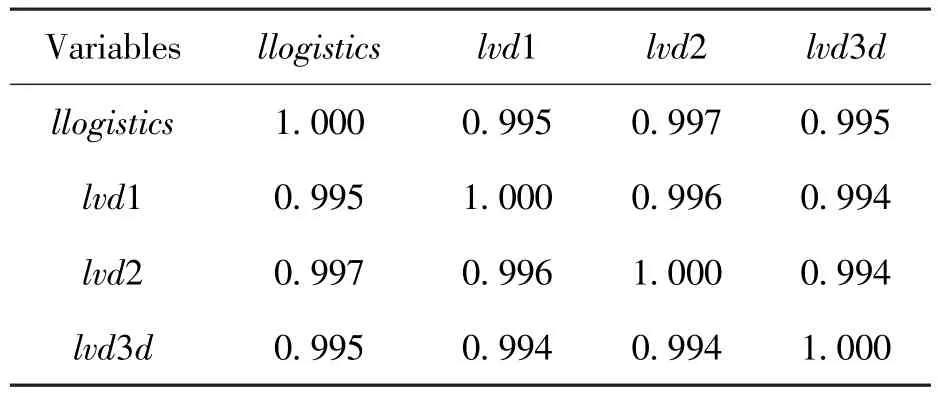
表1 各变量之间的相关性分析

2.3 单位根检验

在建立模型之前，需对各时间序列变量的平稳性进行检验，以保证分析的有效性。本文采用单位根 ADF（Augmented Dickey-Fuller）方法来检验各变量的稳定性。检验结果显示在表2中。

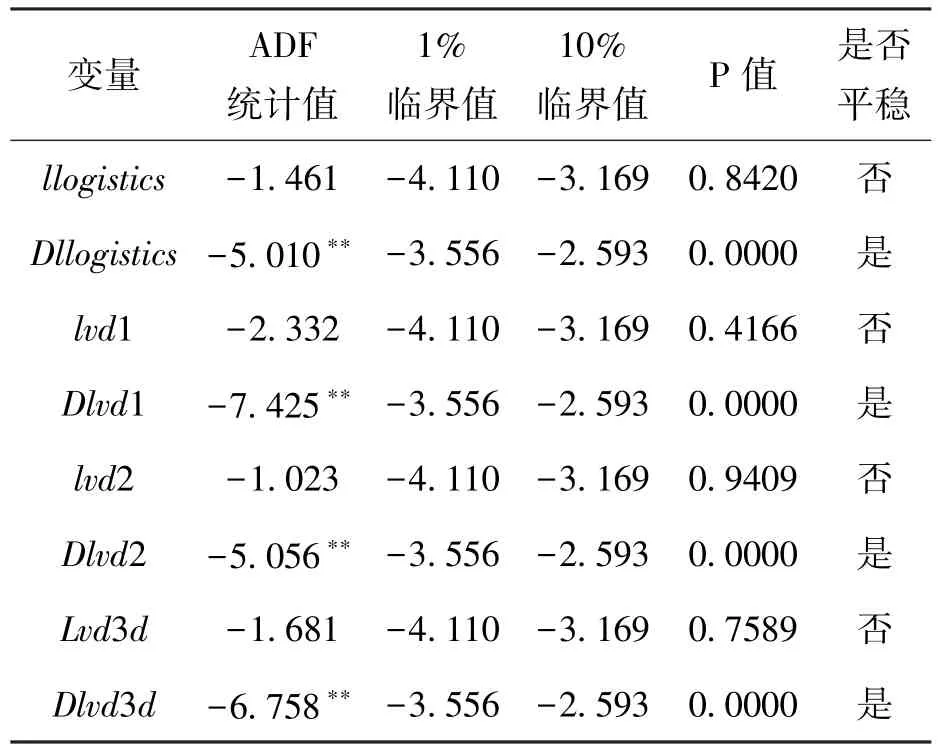
表2 各变量ADF单位根检验结果

由表2中ADF单位根检验结果可知，变量llogistics（交通运输、仓储和邮政业增加值）ADF统计值等于-1.461，即使在10%的显著性水平下，也明显大于临界值-3.169，所以不能拒绝变量llogistics有单位根的原假设，即存在单位根，此变量不平稳；对变量llogistics进行一阶差分，得到Dllogistics，即物流业增长率，再对Dllogistics进行ADF检验，由表2可知，ADF统计值为-5.010，明显小于1%临界值-3.556，检验结果拒绝存在单位根的原假设，也就是说数据不存在单位根，即时间序列变量Dllogistics数据是平稳的。同理，本文对变量lvd1和变量Dlvd1（第一产业增长率）、变量lvd2和变量Dlvd2（第二产业增长率）、变量lvd3d及变量Dlvd3d（第三产业增长率）进行ADF单位根检验，得到lvd1、lvd2和lvd3d是不平稳的时间序列变量，Dlvd1、Dlvd2和Dlvd3d是平稳的时间序列变量，也就是说物流业增长率、第一产业增长率、第二产业增长率及第三产业增长率是平稳的时间序列变量。

3 物流业与三次产业间短期增长关系

llogistics、lvd1、lvd2和lvd3d的一阶差分都是平稳序列，满足了对Dllogistics、Dlvd1、Dlvd2及Dlvd3d进行VAR模型构建的条件。本文根据相关信息准则来确定向量自回归模型（Vector Autoregres⁃sion，VAR）阶数，确定模型滞后2阶。下面从格兰杰因果关系检验结果、脉冲响应函数及预测方差分解3个方面分析相关变量之间的短期关系。

3.1 格兰杰因果关系检验

Granger因果检验是用于检验两个变量之间因果关系的一种常用方法，格兰杰检验的基本原理是将来不能预测过去。通过格兰杰因果检验得到如表3的结果。

从表3可以看出3个原假设对应的P值均明显小于0.05，说明在显著性水平为5%的情况下，表中3个原假设被显著拒绝，即拒绝变量Dlvd3d不是变量Dllogistics的格兰杰原因，拒绝变量Dl⁃logistics不是变量Dlvd1的格兰杰原因，以及拒绝Dlvd2不是Dlvd3d的格兰杰原因；也就说明在5%的显著性水平下，第三产业增长率是物流业增长率的格兰杰原因，物流业增长率是第一产业增长率的格兰杰原因，第二产业增长率是第三产业增长率的格兰杰原因。

3.2 脉冲响应分析

通过VAR模型分析物流业、第一、二、三产业发展之间短期动态相关关系，在此利用脉冲响应函数来分析变量Dllogistics（物流业增长率）在受到自身及其他变量的一个标准差变动后产生的响应。正交脉冲响应函数在收敛的情况下，才会有经济意义。由结果图3可知，各正交脉冲响应函数均收敛。

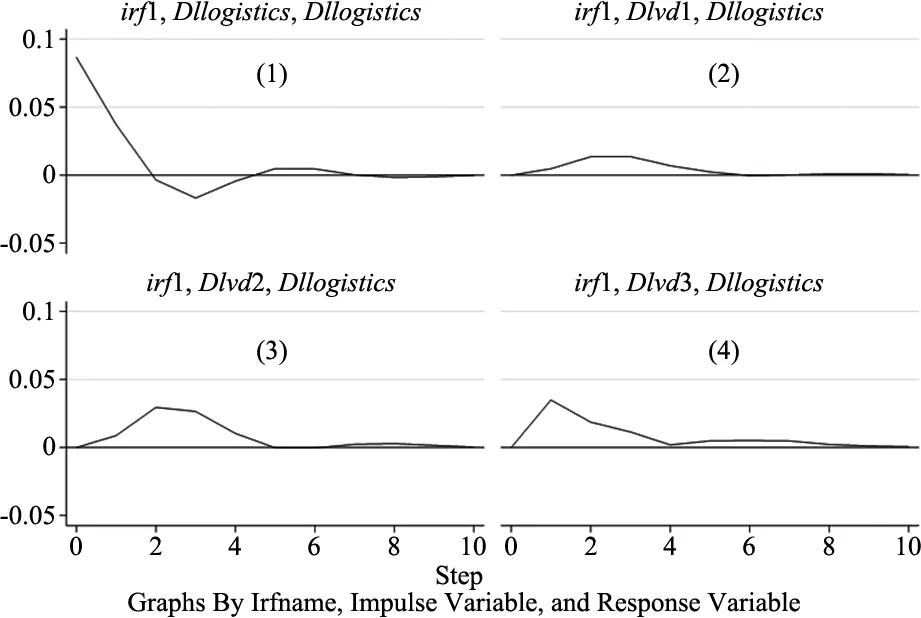
图3 Dllogistics作为响应变量时的脉冲响应图

图3中 （1）表示的是物流业增长率在受到自身一个标准差的冲击下的响应情况，可知在受到自身的一个标准差冲击之后，初期物流业增长率为正向响应且较显著，但其响应程度在第2期便降为0，说明物流业增长率受自身的冲击影响在短时间内较显著，在第3期变为程度较小的负响应，第4期又回到0值，之后没有较明显的波动现象。图2中 （2）～（4）分别表示物流业增长率在受到变量Dlvd1（第一产业增长率）、Dlvd2（第二产业增长率）、Dlvd3d（第三产业增长率）的一个标准差冲击做出的响应情况；物流业增长率对三者的响应均为正向响应，且大致在第4期都归为0值，物流业增长率对第二产业增长率及第三产业增长率的冲击响应更显著于第一产业增长率的冲击响应，这说明第一产业的冲击波动对物流业的影响较小，第二产业和第三产业的冲击波动对物流业影响更大。

3.3 预测方差分解

如图4所示，对VAR模型进行预测方差分解检验，结果显示变量Dllogistics波动主要来自于自身，其次来自于变量Dlvd2和变量Dlvd3d，变量Dlvd1对物流的波动冲击影响不明显。此结果与脉冲响应函数结果相互印证。

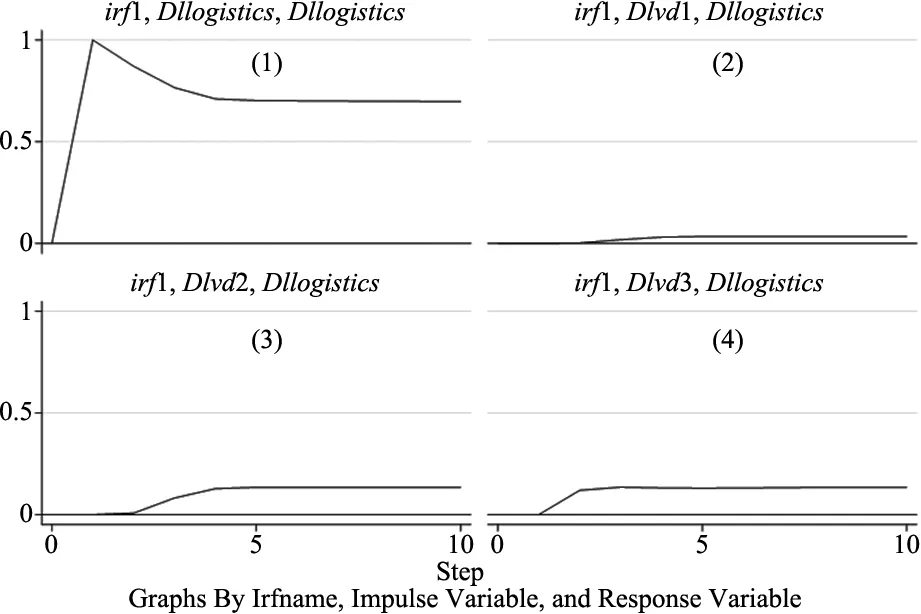
图4 Dllogistics作为预测变量时的预测方差图

本文对各变量之间的短期动态关系进行了检验分析，结果表明短期中物流业增长率和三次产业增长率之间呈现少量单向的格兰杰因果关系，第一、二、三次产业增长率变化的冲击对物流业增长率造成的影响较小，且冲击影响时间短。

4 物流业与三次产业间长期增长关系

从前文的ADF单位根检验可知，各时间序列变量均满足进行协整检验和构建误差修正模型的条件，即时间序列变量llogistics、lvd1、lvd2和lvd3d均为一阶单整序列。本文对物流业发展与三次产业发展之间的长期关系进行深度探究。

如图3所示，为减少饱和湿烟气的加热热量，可以先将脱硫装置出口的饱和湿烟气进一步降温除湿，使其从饱和状态点A到达饱和状态点A′，然后再沿着绝热加热线将饱和烟气状态点A′加热至状态点B′，达到与白雾治理常规方案一样的效果。但由于先对饱和湿烟气进行了降温除湿，因此大大减少了烟气的加热热量，此外，有条件可以进一步利用饱和烟气从状态点A降温至点A′的余热，提高节能效果。

本文运用Johansen协整分析方法来检验长期协整关系是否存在。根据前文本文确定滞后阶数2阶，运用Stata16.0检验变量间的协整关系个数，结果如表4所示，从结果可以清晰地看到标记有 “∗”的迹检验统计量，其对应rank＝2；在协整秩rank＝1时，迹检验统计量为38.5546，由于 “迹检验”（trace test）是似然比检验，故为单边右侧检验，即越大，则越倾向于拒绝原假设。此时迹检验统计量大于临界值29.68，在5%的显著水平下拒绝 “至多存在一个协整关系”的原假设；当rank＝2时，迹检验统计量为13.281，显著小于临界值15.41，说明在5%的显著性水平下不能拒绝 “存在至多两个协整关系”的原假设，结果表明在4个非平稳变量中存在两个长期协整关系。

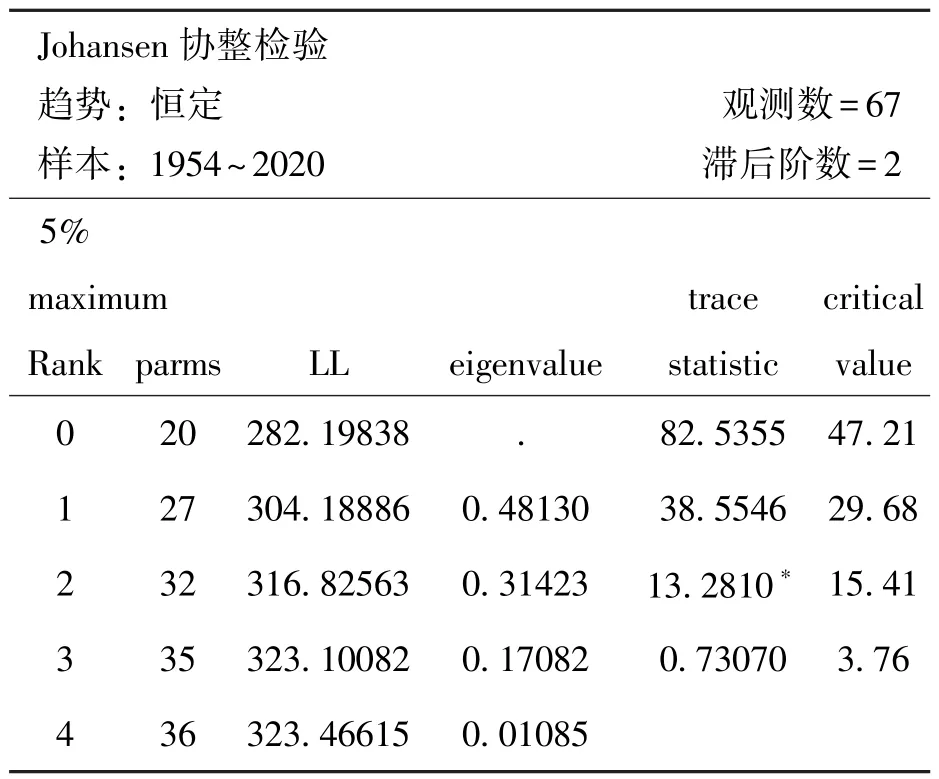
表4 Johansen协整关系个数检验结果

构建VECM模型，如式 （1）：

其中，C是4×1的常数列向量；DYt是由各变量的一阶差分组成4×1的列向量；Yt-1是滞后1期的各变量以及常数项组成的5×1的列向量；X是差分滞后项组成的4×1的列向量；εt是扰动项组成的4×1的列向量。其中：

α为4×2的调节向量，修正长期协整关系中冲击的影响，以保持各变量之间的长期协整关系。β为 5×2 的协积向量，且β′Yt-1～I（0），即可以组成一个平稳的系统。

接着，利用Johansen的MLE的方法估计该系统的向量误差修正模型（Vector Error Correction Model，VECM）；得到表5和表 6所示的结果，本文研究的重点在于各变量之间的长期协整关系，故侧重分析解读以下参数向量值：

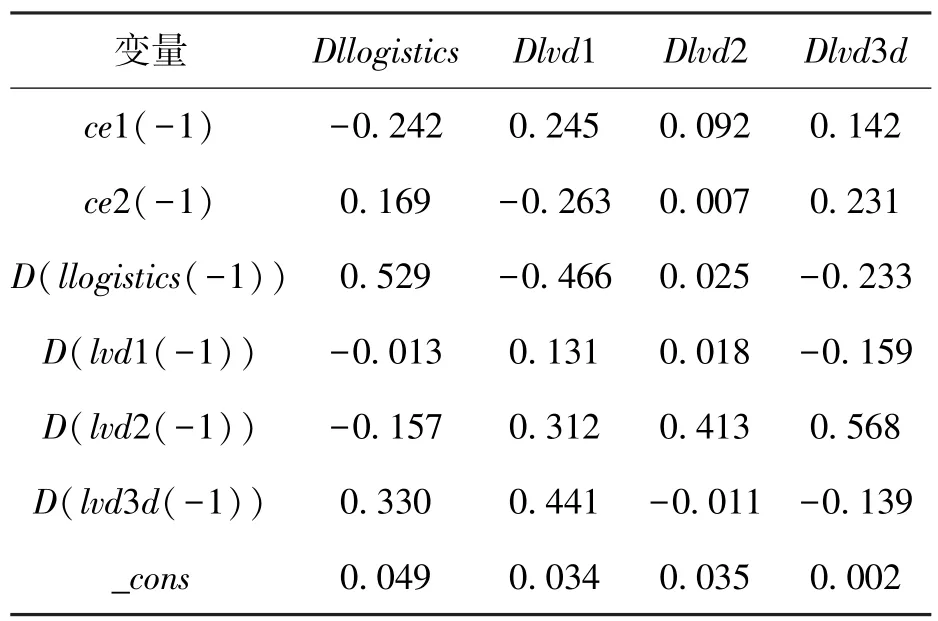
表5 VECM模型计算结果

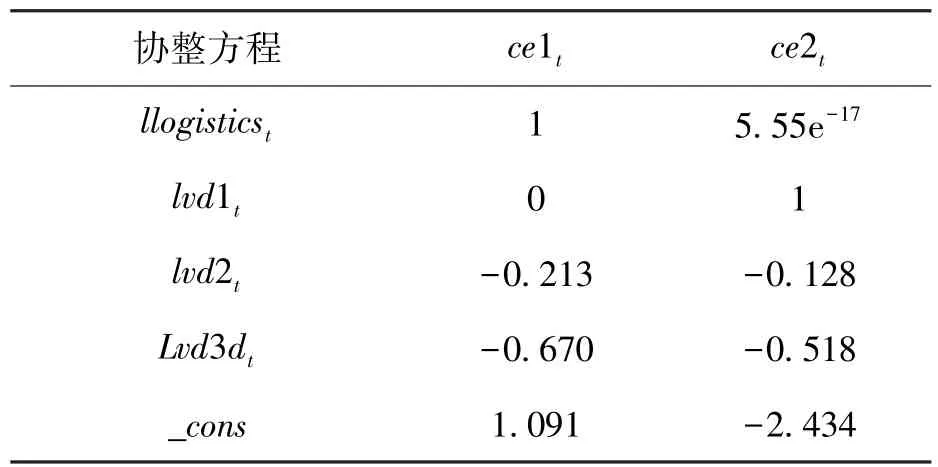
表6 长期协整关系相关参数值

至此，可以得到两个协整关系的表达式分别为：

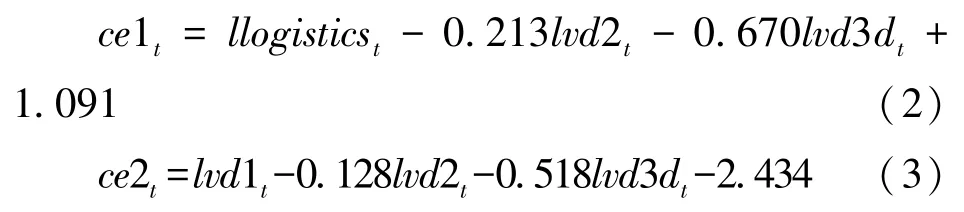
以上两个长期协整关系方程不能将物流业与第一、二、三产业全部包括在同一个长期协整关系中，本文利用VECM模型得出同时含有物流业与三次产业的长期协整关系。

其中：

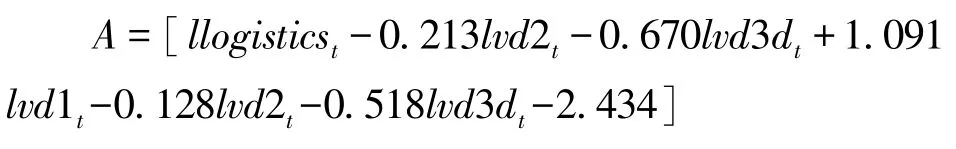
根据以上的VECM模型，选取VECM模型的第一个方程式：

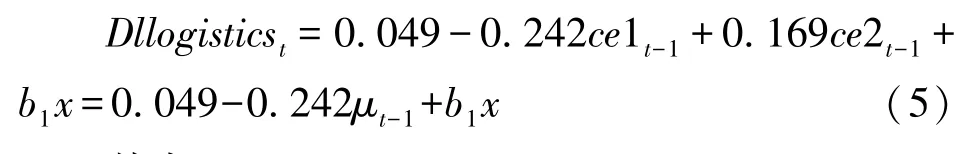
其中：

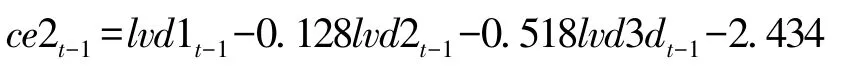
因为方程式 （5）等式左边是平稳的，故可知方程等式右边也是平稳的，因为b1x是各变量差分项滞后1期构成的多项式，故也是平稳的，此时可知μt-1也是平稳的，于是得到：

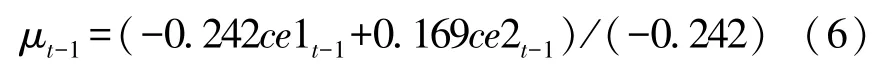
调整到第t期得到：

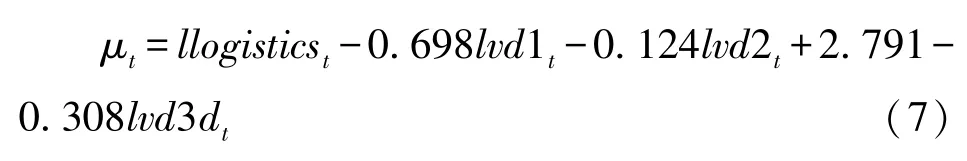
即：

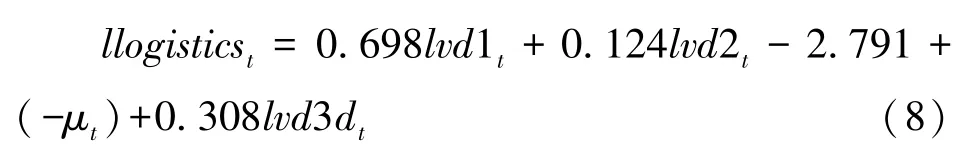
根据含有4个变量的协整关系式 （8）可知，从长期来看，变量lvd1t的系数为0.698，表明第一产业增长与物流业增长的弹性为0.698，即第一产业每增长1个百分点，则物流业增长0.698个百分点，说明第一产业与物流业间具有紧密的关联关系。变量lvd2t的系数为0.124，即第二产业增长与物流业增长之间的弹性系数为0.124，表明第二产业每增长1个百分点，则物流业增长0.124个百分点，第二产业增长与物流业增长间有较紧密的关联关系。变量lvd3dt的系数为0.308，表明第三产业增加值每提高1个百分点，则物流业增长0.308个百分点，说明第三产业增长与物流业增长间具有程度较高的紧密的长期协整关系。

为了更清晰的解释物流业与第一、二、三产业之间的关系，本文选择以物流业增长率变量为被解释变量的表达式即式 （5）：

整理得到：

由式 （9）可知，对于此方程而言，长期协整关系的误差修正系数为-0.242，这说明在此长期协整关系中如果在前一期出现偏离均衡状况的情况，则紧接下来的一期，会得到反向修正和调整，修正程度大约为24.2%，即若出现短期的非均衡状态，误差将会被一定程度的反向修正和调整，使得长期协整关系尽可能地恢复到长期均衡状态。

对此VECM模型的稳定性进行检验，从图5中可以看到，除了VECM模型本身所假设的单位根之外，伴随矩阵的所有特征根均落在单位圆之内，即此VECM系统平稳。但有部分特征根分布离单位圆圆心较远，说明冲击给模型带来的影响持续时间较长。

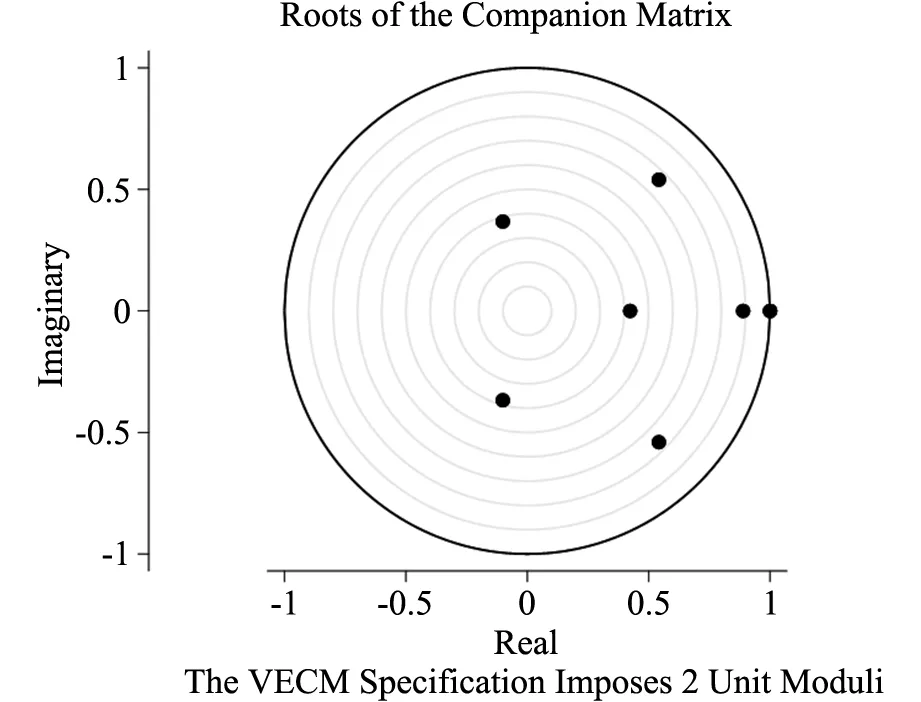
图5 VECM模型稳定性检验结果

5 结论与启示

通过以上的分析，本文得到如下的结论及相关启示。

5.1 结论

（1） 短期关系

短期中，基于VAR模型，根据格兰杰因果检验结果可知，第三产业增长率和物流业增长率有显著的单向动态相关性，物流业增长率和第一产业增长率有明显的单向动态相关性，第二产业增长率和第三产业增长率同样有明显的单向动态相关性。即短期中，第二产业发展促进第三产业的发展，第三产业的发展对物流业发展有较大的促进作用，物流业的发展对第一产业的发展有显著的正向影响。根据脉冲响应函数及预测方差分解分析，得到第一、二、三次产业增长率变化的冲击对物流业增长率造成的影响较小，且冲击影响时间短。总体上看，物流业与三次产业在短期中的增长关系不紧密。

（2） 长期关系

长期中，基于VECM模型，得到物流业、第一、二、三产业之间的长期协整关系，可以看到，物流业发展与第一、二、三产业发展之间存在两个长期协整关系，整合为一个方程后，结果表明第一产业增长与物流业增长的弹性系数为0.698，第二产业增长与物流业增长的弹性系数为0.124，第三产业增长与物流业增长之间的弹性系数为0.308。通过VECM模型可知，在长期协整的过程中，短期的非均衡状态会被修正和调整，即如果在t-1期出现偏离均衡状况的情况，则在t期，会得到反向修正和调整，对于本文中以物流业发展相关变量为被解释变量得到的关系方程中，修正系数为-0.224，大约会有22.4%的偏离会被反向修正。

5.2 启示

（1）科学发展物流产业

物流产业和其他产业长期中存在正向关系，物流产业为其他产业发展提供保障，因此需要高质量发展物流产业；另外，短期中物流业不是第二和第三产业增长的格兰杰原因。因此需要避免在短期中刻意高速发展物流业来推动其他产业发展。

（2）形成合理的产业结构

由物流业与三次产业间的长期协整关系可知，物流业与第一、二、三次产业的弹性系数不同，这表明三次产业的增长与物流业增长之间的关系存在差异，应根据长期协整关系进行资源的合理分配，形成合理的产业结构。

由于所收集数据的有限性，本文研究具有一定的局限性，但在探究及优化物流业与国民经济三次产业增长间的关系方面具有较大的现实意义。

注释：

①本文用不包括物流业的三次产业代表其他国民经济。