匡门口流域极端降水与ENSO相关性分析
张文达,任 政
(1.河北工程大学 水利水电学院,河北 邯郸 056038; 2.河北省智慧水利重点实验室,河北 邯郸 056038)
1 概 述
随着全球不断变暖,极端降水事件显著增加,预计在21世纪末,极端降水将会更加频繁和强烈。据研究表明,近几年我国极端降水事件也发生了变化。如卢珊等研究发现近56年我国极端降水事件在不断增加,极端降水事件出现的时间也有明显的变化,但华北地区极端降水事件却存在不明显的下降趋势[1]。河北省邯郸市在1974-2015年极端降水指数多处于下降状态,杜亮亮等发现极端降水与气温存在极为密切的关系[2]。
ENSO作为热带太平洋地区海气系统年际气候变率的强信号,不少研究指出它对我国的降水存在间接的影响。李海燕通过研究发现ENSO及其组合模态对我国东部各个季节的降水具有影响,尤其是在秋季和东西影响比较明显[3],但对同期影响的研究较少。刘占明等通过使用MK检验、滑动t检验等方法对广东北江流域分区域降水时空分布与Nino3区SST进行了相关性分析,发现与各个站的相关性关系与人类活动的影响[4]。为了进一步探讨ENSO对极端降水的影响,有必要更加系统地分析两者的相关性关系。
应用RclimDex软件对匡门口流域的降水进行极端降水指数计算,通过经验模态分解(EMD)分析极端降水指数与ENSO的相关性分析[5],并运用小波分析的方法对极端降水指数经验模态分解的第一个信号与ENSO进行滞后关系分析。通过分析匡门口流域极端降水指数与ENSO的关系,尝试得出ENSO效应对流域降水年际变化的影响,深入了解极端降水的年际变化机理。
2 研究区概况
匡门口流域位于山西省与河北省交界的清漳河上,流域面积是1 220 km2(图1)。该流域属于干旱季风气候,降水主要受太平洋东南季风影响,年际降水量相差较大,多年平均降水量557.5 mm,最大年降水量为1 459.5 mm,最小年降水量为197.6 mm;降水分配不均匀,多年平均最大月降水为890 mm,最小月降水量为0 mm。

图1 研究区域及雨量站位置图
3 数据与方法
3.1 数 据
降雨数据为匡门口流域及周边附近共25个雨量站点的57年(1959-2015)逐日降雨量;Nino3.4区兼顾到Nino3区(5°N-5°S,150°E-90°W)和Nino4区(5°N-5°S,160°E-150°W),对热带太平洋来说,有着更好的代表性,得到了广泛的认可,故选取该地区海表温度SST数据[6]。
3.2 方 法
3.2.1 极端降水指数
气候指数基于日气温和日降水量数据,采用软件RclimDex计算而得,这其中有27个指数被认为是核心极端气候指数。根据我国华北地区持续干旱现象及极端降水的区域性和局地性特征[7],在11个极端降水指数中选取4个极端降水指数,具体指数内容见表1。

表1 极端降水指数名称及定义
3.2.2 经验模态分解
经验模态分解(Empirical Mode Decomposition,EMD)方法原理是将信号的波动和趋势按照不同尺度分解开,并形成一系列不同特征尺度的数据序列。该方法适用于处理非平稳数据序列,一个内在模函数(Intrinsic Mode Function,IMF)即代表一个序列,最低频率的IMF分量代表原始信号的总趋势或均值的时间序列[8]。
3.2.3 小波分析
1) 连续小波变换。相较于实数形式的小波,复数形式小波在应用中具有明显的优势,其实部与虚部位相相差π/2,通过消除实数形式子波变换系数模的振荡,能更好地得到序列振幅和相位两方面的信息。
ψ0(t)=π-1/4eiε0te-t2/2
(1)
式中:t为时间;ε0为无量纲频率,通常取6。
时间序列的小波变换可表示为:
(2)
式中:Wβ*(α,β)为小波变换系数;ψ*为其共轭复函数;α为尺度因子;β为时间平移因子;δt为采样时间间隔。
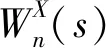
(3)

3) 小波相干。小波相干谱等价于两个交叉小波变换间的局部相关系数,基于Xn和Yn时间序列的交叉小波变换的小波相干谱定义为:
(4)

4 结果与分析
4.1 极端降水与ENSO相关性分析
根据过零点的个数计算IMF的平均周期。将过零点的个数设为N,则该模态具有约(N-1)/2个周期,然后通过将时间长度除以周期的个数来获得IMF振荡周期。虽然一个IMF可能包含不同尺度的变化信号,但相同时间段内,IMFs分量却包含了不同尺度的波动信号,见表2。ENSO在年际尺度上具有准3.3年(IMF1)和准7年(IMF2)的变化周期,在年代际尺度上具有准16.3年(IMF3)和准38年(IMF4)的变化周期,在百年尺度上有约114年(IMF5)。在极端降水指数中,CDD、PROPTOT、R20、R95P指数均与ENSO具有基本一致的震荡周期,并都检测到百年信号,因此ENSO与CDD、PROPTOT、R20指数具有良好的相关性。而CWD两个极端降水指数具有6个IMF信号,其中前两个信号的震荡周期与ENSO的震荡周期基本一致,而这两个指数的IMF3和IMF4与ENSO的IMF4的震荡周期相对应,ENSO的IMF3信号的震荡周期比两个极端降水指数的IMF3大但比IMF4小,这表明CWD指数还受其他因素的影响。而ENSO与两个极端降水指数均具有百年信号,因此两者在周期尺度上也具有良好的相关性关系。

表2 极端降水指数及ENSO各模态(IMF)的平均周期
4.2 极端降水与ENSO相位关系分析
在连续小波分析(图2)中,ENSO(图2a)的峰值主要出现在2~8 a波段,主要有准2~4 a周期(1965-1975和1990-2000年),准3~8 a周期(1980-1990年)3个显著周期(通过了95%的置信区间,下同),显著周期由短周期变成长周期,由此可以看出,ENSO的变化频率在减慢。CDD(图2b)的功率主要发生在峰值主要出现在2~8 a波段,仅有一个准2~4 a周期(1990-2000年),在1965-1975年之间也出现了高能量区,但未通过95%置信区间。与ENSO在准2~4 a周期(1990-2000年)具有一致的显著周期。CWD(图2c)的功率峰值主要在2~8 a波段,有准4a左右周期(1980-1990年)和准3~8 a周期(1995-2005年)两个显著周期,与ENSO在4 a左右周期具有一致的显著周期。PROPTOT(图2d)的功率主要发生在峰值主要出现在2~6 a波段,有准3~6 a周期(1965-1970年)和准2~4 a周期(1990-2000年)两个显著周期,与ENSO在2~3 a(1990-2000年)具有一致的显著周期。R20(图2e)功率峰值主要出现在2~8 a波段,有准2~6 a周期(1965-1970年)显著周期,与ENSO在2~4 a(1965-1975年)具有一致的显著周期。因此,选取的4个极端降水指数与ENSO具有良好的相关关系。
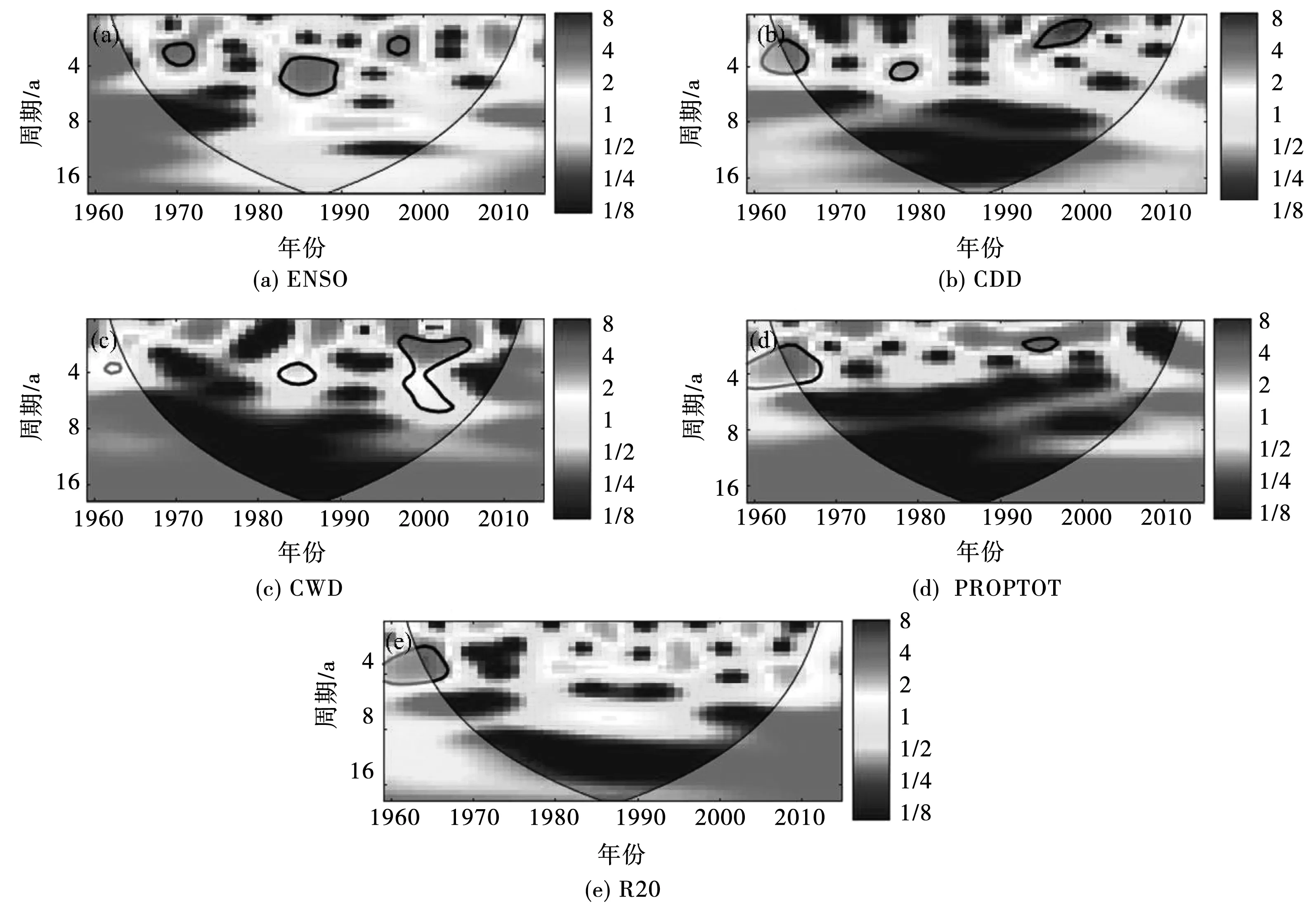
图2 连续小波功率谱 注:图中粗黑色轮廓表示95%置信水平的红色噪声,而边缘效应可能因图像失真使影响锥(COI)显示为较浅的色调,红色和蓝色分别代表能量的峰值和谷值,下同。
交叉小波功率谱能够较好地反映两个信号中均具有较高能量的信号部分,也就是两个信号的共振周期部分。但是其缺点是不能更好地反应两个信号在时间-频率空间内的相位关系,而小波相干分析则能很好地解决这个问题。
在交叉小波变换(图3)与小波相干(图4)分析中,CDD的交叉小波功率谱高能量区(图3a),在1968-1974和1993-2000年存在3~4 a共振周期,箭头方向为左下方,ENSO与连续无雨日数超前3/8个周期,为非线性相关关系,在1980-1990年存在4~7 a共振周期,箭头朝右,两者为正相关关系;在小波相干功率谱低能量区(图4a),1980-1990年存在4~6 a共振周期,两者为正相关关系;在1995-2000年存在2~4 a共振周期,ENSO与连续无雨日数超前3/8个周期,为非线性相关关系。

图3 交叉小波能量谱注:图中箭头表示相位关系,→表示同相位,为正相关;←表示反相位,为负相关,下同。
CWD的高能量区(图3b)中可以看出,在1972-1975年存在2~3 a共振周期,箭头方向朝下,相位关系超前1/4个周期;在1995-2000年存在2~4 a共振周期,方向为右下方,相位关系为提前1/8个周期;在1980-1990年存在3~7 a共振周期,箭头方向朝左下方,相位关系为超前3/8个周期;在1985-2005年存在4~8 a共振周期,方向朝右上,相位关系滞后1/8个周期;低能量区(图4b)中,在1970-1975年存在2~3 a共振周期,箭头方向朝下,相位关系超前1/4个周期;在1980-1990年存在3~7 a共振周期,箭头方向朝左下方,相位关系为超前3/8个周期;在1995-2000年存在5~7 a共振周期,箭头朝右上,相位关系滞后1/8个周期。PROPTOT的高能量区(图3c)可以发现,在1967-1970年存在3~5 a共振周期,箭头朝左下,相位关系超前3/8个周期;1982-1990年存在4 a个周期,方向朝左下方,相位关系超前3/8个周期;在1995-2000年存在2~4 a共振周期,箭头朝向右下方,相位关系超前1/8个周期,为非线性相关关系。而低能量区(图4c)中,在1985-1990年存在4 a共振周期,方向朝下,相位关系超前1/4个周期;在1990-2000年存在2~3 a共振周期,方向朝右下方,相位关系超前1/8个周期。R20的高能量区(图3d)在1965-1970年存在3~5 a共振周期,但是相位关系不明确;在1998-2003年存在5~6 a共振周期,方向朝左,相位关系为负相关关系;在低能量区(图4d)中相位关系均未通过95%的置信检验。
5 结 论
通过对极端降水指数与ENSO进行相关性分析及对EMD分解的第一个信号分析滞后关系,得到以下结论:
1) 通过分析极端降水与ENSO的相关性发现,CDD、PRCPTOT、R20指数均分解得到5类信号,这些极端降水指数的周期分别在3、8、24、38、114左右,和ENSO的信号周期基本一致,在IMF2、IMF3上有一些差别,但是差别不太大;并都分解到了百年信号,表明ENSO与这5个指数之间相关性良好。CWD分解出6个信号,周期分别在3、7、13、23、38、114左右,IMF1、IMF5、IMF6与ENSO的IMF1、IMF4、IMF5相对应,ENSO的IMF3介于这两个指数的IMF3和IMF4之间,表明这两个指数还受其他因素的影响。
2) 通过分析极端降水与ENSO的滞后关系,极端降水指数中的峰值大多分布在2~8 a波段,周期长度变化不一。ENSO比各个主要极端降水指数超前1/8或3/8个周期,为非线性相关关系;只有CWD、指数在2000年左右有滞后1/8个周期的现象,这表明这4个指数受其他因素如人类活动的影响,相关性关系发生变化。

