基于直觉犹豫模糊集的群体决策规则提取方法

司 瑾，李洪波，2

(1. 长春工程学院，吉林 长春130012；2. 长春工业大学计算机学院，吉林 长春130012)

1 引言

在市场竞争越来越激烈的年代，一个决策的优劣直接关系到一个企业的生死存亡，因此如何做出一个好的决策成为各大企业面临的首要问题。然而，由于社会环境的复杂性，市场的多变性，决策过程要考虑的因素也越来越多的，再加上事物本身的不确定性和模糊性，要想做出科学合理的决策十分困难[1]。

面对上述问题，关于决策方法的研究有很多。如文献[2]中构建一种基于区间直觉犹豫模糊集的决策模型，该模型定义了提取规则与部件之间的关系，利用该模型来找出能够识别高速列车系统关键部件；文献[3]中采用犹豫直觉模糊语言集对决策者的初始决策矩阵进行赋值，然后计算两个犹豫直觉模糊语言数之间的距离，以距离的长短决策出危险品多式联运系统中的风险最低的方案。

在前人研究经验的基础上，提出一种基于直觉犹豫模糊集的群体决策规则提取方法。该方法首先进行相关信息的集成，然后对信息处理，提高信息质量，接着将整理好的信息组成决策问题中的初始属性集，最后构建基于直觉犹豫模糊集的群体决策模型，利用该模型提取决策规则。最后将所研究的方法应用到一个实例问题当中，即配送中心选址问题上，选择出一个性价比最高的厂址方案，证明了所研究方法的有效性。

2 群体决策规则提取模型研究

群体决策规则提取是指依据大数据分析技术，对众多决策进行评估，根据综合评分结果选取最优方案。本文要研究的是如何利用直觉犹豫模糊集理论，将方案模糊化，从而解决专家在进行方案选择时的犹豫不决的问题。

2.1 群体决策基础信息的集成

群体决策的关键在于需要大量数据信息作为支撑，因此在群体决策规则提取前，基础信息的收集和集成工作是必不可少。群体决策基础信息的集成方法有很多，在这里采用一种爬虫+数据仓库集成的方法，即在利用爬虫技术在网络收集信息后，直接进入数据仓库，在数据仓库中进行整理和归纳。

1)信息爬虫

信息爬虫是一种在互联网上搜索相关信息的技术，其基本流程如下图1所示。

图1 信息爬虫基本流程

首先插入种子URL到网络上，然后进行网页抓取。抓取完成后，利用网页分析算法对网页上包含的信息进行提取并解析，再然后计算信息与主题之间的相关性，通过相关性过滤掉无关的冗余信息和链接，保留下与决策主题相关的信息，并保存在数据仓库当中，等待下一步的利用[4]。

2)数据仓库

数据仓库是一种数据集成工具，其建立步骤如下：

步骤1：收集和分析业务需求，建立数据模型和数据仓库的物理设计。

步骤2：定义数据源，选择数据仓库技术平台。对原始数据集当中的数据进行处理，包括清洗、去噪、格式统计等，然后将处理好的数据抽取出来并放入到建立的数据仓库当中。

步骤3：选择访问和报表工具，为了能够在后期，用户能够直接从数据仓库当中提取出所需要数据，选择连接软件，将数据仓库与用户终端连接起来。

步骤4：选择数据分析和数据展示软件，更新数据仓库。

2.2 群体决策基础信息属性约简处理

为降低后续群体决策规则提取的难度以及减少计算量，需要对信息属性进行约简，消除冗余和不相关属性，从而使得数据由高维降至低维[5]。数据约简方法有很多种。在这里，利用遗传算法和粒子群算法两种寻优方法来求取属性约简的最小值。

1)遗传算法

遗传算法就是根据优胜劣汰原则而选择出最优质的基因，其基本原理如图2所示。

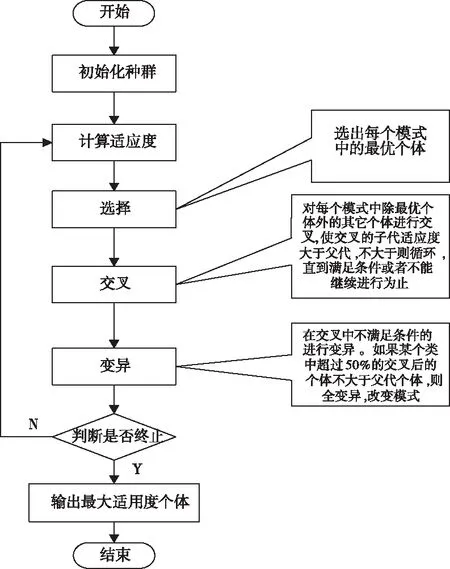
图2 遗传算法基本流程图

遗传算法最大的优点在于在搜索最优解的时候，搜索范围广泛，但是这也就相对降低了算法的搜索收敛速度[6]。

2)粒子群算法

粒子群算法是一种群体智能寻优方法，利用鸟类觅食原理设计而成，具体过程如图3所示。

图3 粒子群算法基本流程

与上述研究的遗传算法存在的优点正好相反，遗传算法的缺点正好是粒子群算法的优点，而遗传算法的优点正好是粒子群算法的缺点。此外，粒子群算法还有一个更为严重的问题，即容易陷入局部最优问题当中[7]。

3)基于遗传粒子群的属性约简

基于上述遗传算法和粒子群算法存在的优缺点，将二者结合在一起，实现优势互补，以此进行属性约简[8]。具体过程如下：

步骤1：输入一个决策表，记为S={U，C∪D，V，f}。计算出决策表中的决策属性D关于条件属性C的依赖度。

步骤2：计算决策表中的条件属性C的属性核，记为Core(C)。判断是否YCore(C)=YC。若等于，Core(C)为最小相对约简；否则，继续进行下一步。

步骤3：初始化种群，并进行参数设置。

(1)

计算粒子群中各粒子的适应度，初始化局部最优值pbest(i)和全局最优值Gbest，设置当前进化次数为1，最大迭代次数。

步骤4：更新粒子速度和粒子位置，计算适应度值。

步骤5：更新t时刻第i个粒子的局部极值和全局极值。判断粒子的局部最优值是否达到最大？若达到最大，则为全局最优粒子。基于步骤4结果进行遗传操作。

步骤6：判断是否达到设置的最大迭代次数？若达到，继续进行下一步；否则，回到步骤5。停止计算，输出全局最优粒子，即为决策表S的一个最小属性约简[9]。

2.3 群体决策规则提取

基于上述环节，将获取到数据分成直觉模糊集和犹豫模糊集，并将二者对应合成为直觉犹豫模糊集[10-11]。下面对各自定义进行分析。

定义1：直觉模糊集Z。

Z={|x∈X}

(2)

式中，X是一个给定论域；FZ(x)→(0，1]和VZ(x)→(0，1]分别代表Z的隶属函数FZ(x)和非隶属函数VZ(x)，且对于Z上的所有x∈X，0≤FZ(x)+VZ(x)≤1成立。当X仅包含一个元素时，直觉模糊集Z={|x∈X}成为直觉模糊数，可记为Z=。

定义2：犹豫模糊集E

E={|x∈X}

(3)

式中，e(x)代表x隶属于E的程度，是[0，1]范围内的一个有限非空子集；当X=1时，E成为犹豫模糊数，即e(x)。

定义3：直觉犹豫模糊集。

设X是一个给定论域(非空集合)，则X上的一个直觉模糊集B为

B={|x∈X}

(4)

基于上述三个定义理论，构建群体决策规则提取模型，其描述如下：假定有n个方案Y={y1，y2，…，yn}，m个决策准则C={c1，c2，…，cn}(准则间相互独立)，W={w1，w2，…，wn}T∈R为准则的权重的向量，且wj∈[0，1](j=1，2，…，m)，rij为yi在ci下的评价值，表示为直觉犹豫模数形式，最后按照从大到小顺序排列，得到最优决策方案[12]。

群体决策规则提取解基本流程如下：

步骤1：根据研究主题采集数据并处理，然后建直觉模糊决策矩阵D=(dij)n·m，如表1所示。

表1 直觉模糊决策矩阵D

式中，dij=(αij，βij)为方案yi关于属性gj的特征信息；αij表示方案yi满足属性gj的程度；βij表示方案yi不满足属性gj的程度，于是得到所有方案yi(i=1，2，…，n)关于所有属性gj(j=1，2，…，m)的特征信息。

步骤2：利用下述式(5)计算yi在gj的得分函数值。

(5)

步骤3：将得到的得分函数值转换为矩阵形式，并进行归一化处理。

步骤4：利用式(6)计算各属性gj的平均信息熵。

(6)

式中，Sij′为归一化处理后的得分函数值。

步骤5：按照式(7)计算各属性gj的权重系数。

(7)

步骤6：按照式(8)计算第i种方案的综合属性值。

(8)

步骤7：根据计算得到的f(yi)值，对方案进行从大到小排序。f(yi)越大，证明决策方案越好。

3 仿真分析

为检验所研究方法的有效性，本章节将方法应用到物流配送中心的选址上，并借助MATLAB2015b工具进行仿真。

3.1 选址方案

网购通过物流配送将商品交付到消费者手上，在购物平台上交易的过程中，物流配送是网购交易达成的最重要的环节，是电商和消费者之间连接的纽带，是货物流传的节点。随着网购量的增大，物流配送面临巨大的压力，迫使各大物流企业不得不增加配送中心点的设置。

配送中心是物流的节点，尤其对于城市而言，配送量更为巨大，因此配送中心的选址问题至关重要，关系到配送时间、配送成本、配送效率、配送业务完成量等等。为此，以某物流在城市中的选址为例，利用所研究的方法进行决策提取，选出最优的配送中心位置。图4为5种选址方案示意图。

图4 配送中心选址方案

这5种方案的属性主要包括四个，即交通条件、辅助性基础设施、市场效益以及政策法规。

3.2 参数设置

仿真中设置的相关运行参数如表2所示。

表2 相关运行参数

3.3 结果分析

在采集并处理相关数据的基础上，构建直觉模糊决策矩阵，如表3所示。

表3 直觉模糊决策矩阵

在式(5)计算下得出得分函数值，如表4所示。

表4 得分函数值表

利用式(8)计算5种选址方案的综合分值，结果如表5所示。

表5 5种方案的综合分值计算

将表5中5种方案的综合分值从大到小排序，方案4>方案5>方案2>方案1>方案3，群体决策规则提取方法效果较好，说明方案4为最优的配送中心选址方案。

4 结束语

多属性决策一直各领域研究的重点，在现代经济快速发展的社会，一个企业或者几个部门、机构要想做出一个合理科学的战略决策，需要考虑的因素众多，因此很难在众多优秀的群体决策中选出最优的一个。为此提出一种基于直觉犹豫模糊集的群体决策规则提取方法。该方法利用直觉模糊数形式对问题进行模糊化处理，以解决很多难以定量分析的问题。经过仿真测试，证实了所研究方法的有效性，为多准则群决策问题提供可靠的依据和参考。