属性集变化条件下集值决策信息系统的增量属性约简方法

刘 超，王 磊*，杨 文，钟强强，黎 敏

（1.南昌工程学院信息工程学院，南昌 330099；2.江西省水信息协同感知与智能处理重点实验室（南昌工程学院），南昌 330099）

0 引言

由波兰数学家Pawlak［1］所提出的经典粗糙集理论是一个强大的数学工具，可用于描述属性间的依存关系，评估属性的重要性，并从决策表中导出规则。运用粗糙集理论还可以用来解决很多带有不确定性、模糊性的实际问题，目前在医学、金融、特征选择、图像处理、语音识别等领域都有着非常重要的应用。

经典粗糙集理论主要是运用不可分辨关系，即等价关系对论域上的对象在属性集上进行划分。它的应用是面向完备系统的，也就是说每个对象的属性值都必须是完整的、精确的、没有缺失值的。然而由于现实因素的影响，数据存在多样性，一个对象的某些属性值可能含有多个值，即决策信息系统中出现了集值型数据。这些集值通常用于描述决策信息系统中的不确定信息和缺失信息。集值决策信息系统被认为是单值决策信息系统的一个重要拓展模型，因此等价关系模型下的属性约简不再适用于集值系统。对此，许多学者针对集值系统进行了一系列的研究。Kryszkiewicz［2］提出了基于容差关系的粗糙集模型；吴鹏等［3］提出了一种基于集值的k度相容关系的粗糙集模型；乔全喜等［4］提出了一种集值系统下基于相对限制容差关系的属性约简方法；Guan 等［5］为了从集值决策信息系统中导出最优决策规则，提出了最大容差类的相对约简的概念，并定义了一种差别函数，通过布尔推理技术计算相对约简；Qian 等［6］针对集值序信息系统提出了一种基于优势关系的粗糙集方法；Dai 等［7］在集值系统中定义了信息熵和粒度测度的概念，并研究了它们的一些性质；Wei 等［8］提出了两种模糊粗糙近似模型，并定义了两种相应的相对正区域约简方法；马建敏等［9］在集值信息系统中基于相容关系给出了信息量的概念，提出了一种启发式约简方法；刘莹莹等［10］将相似度的概念引入到集值信息系统中，对无核型的集值信息系统求取属性约简更加有效。以上研究均是基于静态下的集值系统，对于一部分问题能够得到有效处理。

在实际应用中，许多实际信息系统的属性集会发生动态变化，由此属性约简的结果也会随之而变化。非增量式方法通常是不可行的，这是由于它们需要从头开始计算并消耗大量的计算时间，而增量式方法被认为是处理动态变化数据的有效技术，因为它们可以在先前的计算结果基础上直接进行计算。鉴于集值决策信息系统中数据的动态变化，许多学者在此方面进行了系统、深入的研究。如：Zhang 等［11］在集值系统中提出了一种构造关系矩阵的方法来求解上下近似，并且在属性增加时给出了相应的增量式方法来更新近似集；邹维丽等［12］给出了在相容关系和拟序关系下的集值粗糙集模型的近似增量式更新方法；王映龙等［13-14］针对集值决策系统下属性集增加的情形，提出了一种基于信息量的动态属性约简方法，在对象增加时，讨论了新增对象与分布式约简的理论关系，并提出了一种快速更新分布协调集的增量式方法；Luo 等［15］提出了在集值决策系统中通过增加和删除标准值来计算近似集的增量式方法。上述研究推动了集值决策信息系统领域各方面研究的蓬勃发展，然而，在集值决策信息系统的属性集发生变化条件下有关增量式属性约简方面的研究报道相对较少。

鉴于此，本文针对集值决策信息系统，首先引入集值关系矩阵，随后将知识粒度的矩阵表示方法拓展到集值决策信息系统，并将其应用于启发式属性约简的计算；然后，分析集值决策信息系统在属性增加条件下属性约简的增量机制，设计了一种增量式属性约简方法；最后通过实验验证了方法的有效性。

1 集值决策信息系统基本概念

本章首先介绍集值决策信息系统的基础知识，然后给出集值决策信息系统中集值关系矩阵的定义，在此基础上将文献［16］中知识粒度的矩阵表示推广至集值决策信息系统之中。

定义1集值决策信息系统SDS=(U，A，V，f)。其中：U为非空有限对象的集合；A=C∪D是一个非空有限的属性集合，C是条件属性的集合，D是决策属性的集合，对于∀a∈C∪D，a的属性值Va的取值为一个集合；V是信息函数f的值域，满足V=；f是一个信息函数，它指定U中每一个对象的属性值。

例1 表1 是一个集值决策信息系统，其中U={x1，x2，x3，x4，x5，x6，x7，x8}为论域，条件属性集为C={a1，a2，a3，a4，a5}，决策属性集为D={d}。

表1 集值决策信息系统Tab.1 Set-valued decision information system

定义2给定一个集值信息系统SIS=(U，C，V，f)，对于∀B⊆C，SB是论域U上的集值关系，表示为：

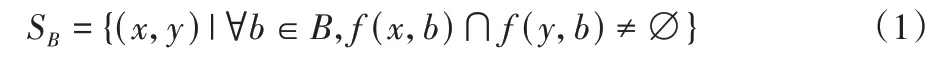
定义3给定一个集值决策信息系统SDS=(U，A，V，f)，A=C∪D，条件属性子集B⊆C，且有∀b∈B，决策属性D={d}，决策属性d所对应的U上的决策划分为U/d={(xi，xj)|(xi，xj)∈U2，f(xi，d)=f(xj，d)}；属性集B∪d的集值关系矩阵为，那么SB∪d(i，j)表示为：

定义4［16］给定一个集值决策信息系统SDS=(U，A，V，f)，对于B⊆C，SB是U上的集值关系，表示集值关系矩阵，参考文献［16］中知识粒度定义方法，那么B在U上的知识粒度定义为：

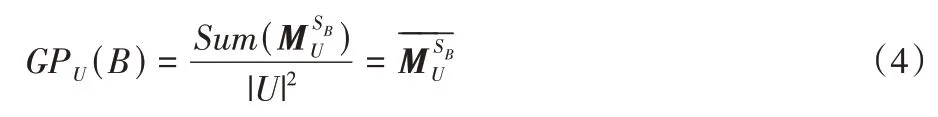
定义5给定一个集值决策信息系统SDS=(U，A，V，f)，对于B⊆C，则决策属性D关于条件属性B的相对知识粒度定义为：

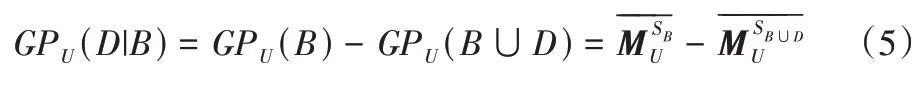
那么条件属性C在U上的知识粒度为，同理可计算出相对粒度GPU(D|C)=。

定义6已知集值决策信息系统SDS=(U，A，V，f)，B⊆C，对于∀a∈B，属性a关于条件属性集B相较于决策属性集D的内部属性重要度定义为：

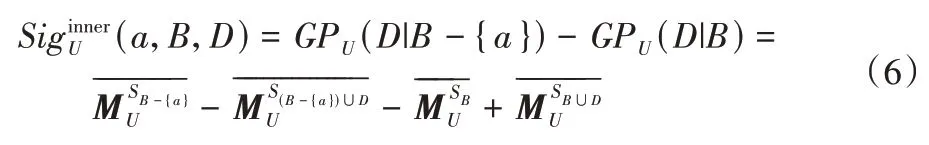
定义7已知集值决策信息系统SDS=(U，A，V，f)，A=C∪D，B⊆C，对于∀a∈C-B，属性a关于条件属性集B相较于决策属性集D的外部重要度定义为：

定义8［17］给定一个集值决策信息系统SDS=(U，A，V，f)，对于B⊆C，B是系统的相对属性约简当且仅当满足以下两个条件：

1)GPU(D|B)=GPU(D|C)；

2)∀a∈B，GPU(D|B-{a})≠GPU(D|B)。

2 基于知识粒度的启发式属性约简

基于知识粒度的启发式属性约简方法（Heuristic Attribute Reduction Method based on Knowledge Granularity，HARM-KG）的具体描述如方法1 所示。

3 属性增加条件下的增量式属性约简

该部分介绍集值决策信息系统属性约简的增量式更新机制。当有新的属性添加到系统中的属性集时，研究新的增量关系矩阵、知识粒度和相对知识粒度发生变化的规律，由此设计相应的增量式属性约简方法，进而更新属性约简。

3.1 属性约简的增量式更新机制

当属性集P添加到集值决策信息系统中时，集值关系矩阵必然会发生相应的变化，从而导致新的知识粒度也随之细化。如果可以运用增量式更新策略来更新知识粒度，而不是从头开始计算，这样势必会减少更新时间。

定义9给定一个集值决策信息系统SDS=(U，A，V，f)，集值关系矩阵。假设P是新增加的属性集，SP是U上的集值关系，并且，那么增量关系矩阵定义为：

定理1给定一个集值决策信息系统SDS=(U，A，V，f)，A=C∪D，B⊆C，条件属性集B增加条件下（B增加为B∪P），知识粒度更新为：

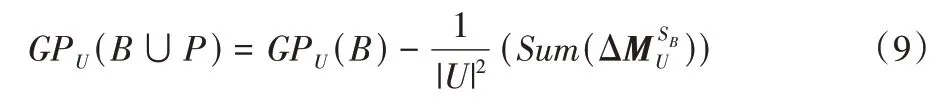
其中：GPU(B)是条件属性为B时的知识粒度；是增量关系矩阵所有元素之和。

证明 由式（4）和式（8）容易证明该定理。

定理2给定一个集值决策信息系统SDS=(U，A，V，f)，GPU(D|B)是相对知识粒度，假设P是新添加的属性集，和分别是增量关系矩阵，然后，则更新后的相对知识粒度变为：

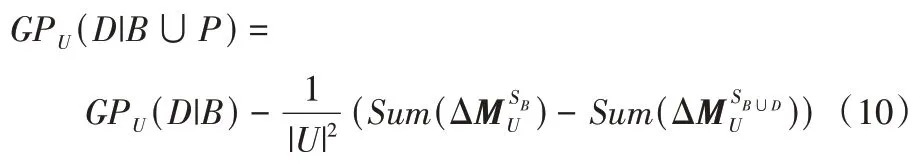
证明 根据式（5）和式（9），有：

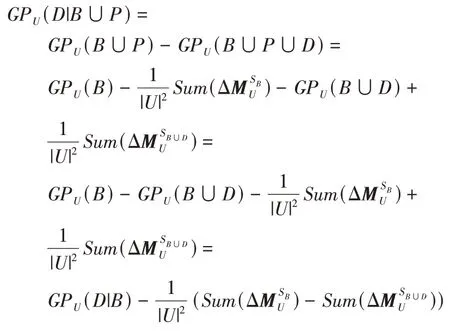
故定理2 得证。

3.2 属性增加条件下的增量式属性约简方法

本节针对集值决策信息系统下属性集的动态变化，构造一种增量式属性约简方法。可概括为以下3 个步骤：

1）根据增量式方法计算更新后的知识粒度；

2）从非核属性集中选择具有最高外部重要性的属性，将其逐步添加到属性约简中；

3）删除属性约简中的冗余属性。

增加属性集时基于知识粒度的增量属性约简方法（Incremental Attribute Reduction Method based on Knowledge Granularity when increasing attribute set，IARM-KG）的具体描述如方法2 所示。

3.3 时间复杂度分析与比较

当属性集P添加到集值决策信息系统时，非增量式方法的时间复杂度讨论如下：计算论域中的相对知识粒度的时间复杂度，即起点的时间复杂度为O((|C|+|P|)|U|+|C||U|)，所以非增量式方法的总的时间复杂度为O((|C|+|P|)2|U|+(|C|+|P|)|U|)。增量式方法的时间复杂度讨论如下：计算新的相对知识粒度的时间复杂度为O((|C|+|P|)|U|+|P||U|)，当属性集增加时，依据原有的属性约简结果，仅需对新增的属性集P进行处理，因此，所提出的增量式方法的时间复杂度为O((|C|+|P|)2|U|+|P||U|)。可以看出，非增量式方法的时间复杂度通常比增量式方法高得多。换句话说，增量式方法比非增量式方法更加快速。

通过上述分析，本文所提出的增量式方法的时间复杂度为O((|C|+|P|)2|U|+|P||U|)。若采用文献［9］中提出的信息量与属性重要性概念来求得属性约简，其时间复杂度为O(|C|2|U|2+|C|3|U|2)；当有新的条件属性集P加入到集值系统中时，方法的时间复杂度更新为O((|C|+|P|)2|U|2+|(C|+|P|)3|U|2)，计算过程复杂，需要消耗大量的时间，本文方法计算用时较短。若采用文献［10］中提出的基于相似度的属性约简方法，时间复杂度为O(|U|2|C|3)；该方法需要计算集值系统中每一个属性的相似度，当新增属性集P添加进来时，总的时间复杂度为O(|U|2(|C|+|P|)3)，也需花费较多时间。因此，本文方法在计算时间上对比于其他方法具有一定的优势。

4 实验与结果分析

4.1 实验数据集

为了验证本文提出的增量式方法的准确性和有效性，本文从UCI 机器学习数据库（http：//archive.ics.uci.edu/ml/index.php）中下载了3 个数据集。为了得到集值数据集，对这3 个数据集进行如下预处理：对含有缺失值的数据集，定义缺失的属性值为其对应属性上的所有属性值的集合；对于完整型数据集，随机选择10%的属性值进行剔除，然后分别对各缺失值取其对应属性上的所有属性值的集合。各数据集的具体信息如表2 所示。

表2 实验数据集Tab.2 Experimental datasets

4.2 实验方案

实验均在PC 上进行操作，实验分析所搭载的硬件环境为：Intel Core i5-8300H CPU @ 2.3 GHz；内存为8 GB；方法在Matlab R2019a 软件平台上编程实现。为了比较非增量式方法和增量式方法的属性约简时间，将每个数据集的属性集分成6 个部分：第1 部分作为原始数据集，剩余部分作为候选集。其中将候选集的第1 部分与第2 部分组合视为第1 增量数据集，将第1 增量数据集与第3 部分组合视为第2 增量数据集，以此类推。然后分析通过增加属性集更新基本数据集后，基于知识粒度的增量式和非增量式属性约简方法的运行效率。

4.3 两种方法运行时间比较

为了验证增量式方法的高效性，本文通过添加属性集来使原始的属性集发生变化，并比较了在不同数据集上非增量式方法和增量式方法的运行时间，实验结果如图1 所示。图1 描述了随着数据集中属性数目的增加，集值决策信息系统中非增量式方法和增量式方法在计算属性约简所消耗时间上的变化趋势。其中x轴表示增加属性集的百分比，y轴表示运行时间。由图1 可得出以下结论：

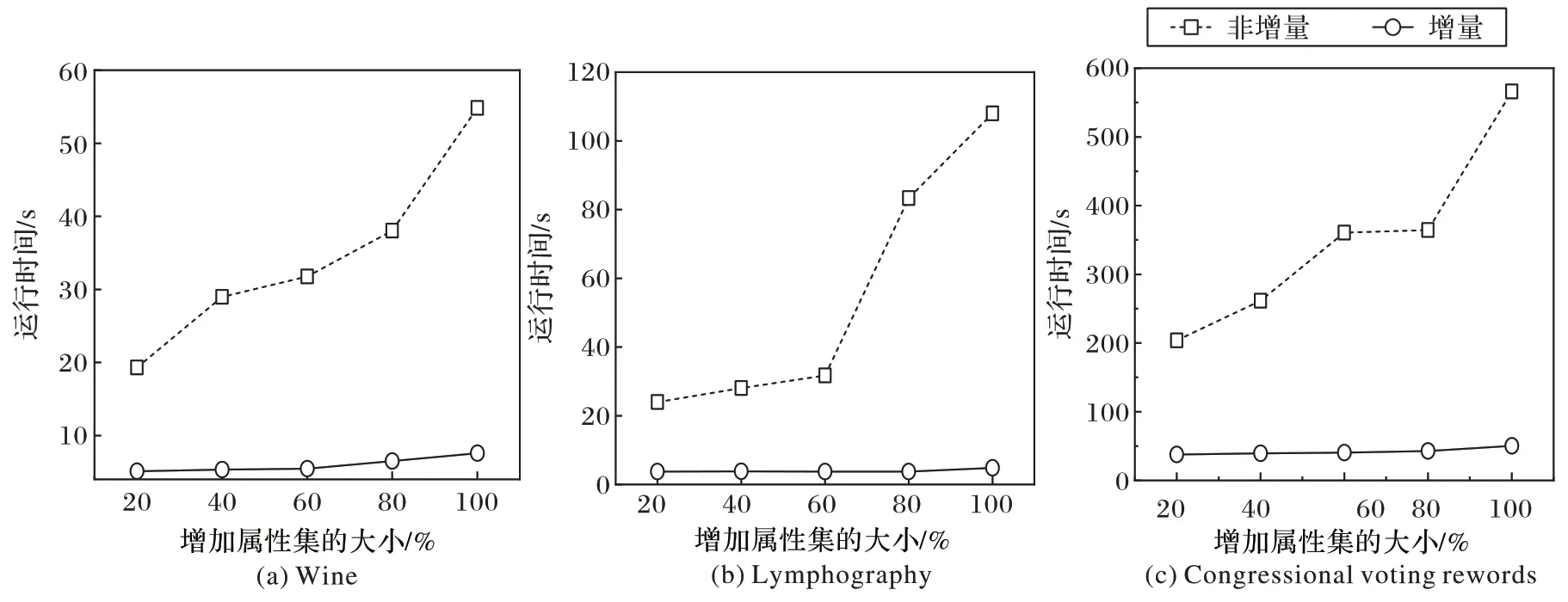
图1 非增量式方法与增量式方法的属性约简时间比较Fig.1 Comparison of attribute reduction time between non-incremental method and incremental method

1）当属性集不断被添加到集值决策信息系统中的原始属性集中时，增量式方法在更新属性约简方面始终比非增量式方法更快；

2）非增量式方法在时间消耗上的增长幅度较大，而增量式方法的增长幅度则较为平缓；

3）随着数据集大小的增加，两种方法在时间消耗上差异越来越明显。

4.4 两种方法的属性约简结果比较

两种方法的属性约简结果如表3 所示。从表3 可看出：非增量式方法和增量式方法的属性约简结果非常接近，并且增量式方法可以在更短的时间内获得一个可行的约简。结果表明，增量式方法能高准确度地获取属性约简。

表3 两种方法的属性约简结果比较Tab.3 Comparison of attribute reduction results of two methods

4.5 分类精度比较

为了验证两种方法得出的约简结果的准确性，在Weka机器学习软件上，用软件自带的贝叶斯分类器进行测试，并通过十折交叉验证的方式来计算非增量式方法和增量式方法所获得的属性约简结果的分类精确度，结果如表4 所示。从表4 可以看出，集值决策信息系统下非增量式方法与增量式方法的分类精确度是十分接近的，在个别数据集上甚至完全相同。这说明本文提出的增量式属性约简方法是可行和有效的。

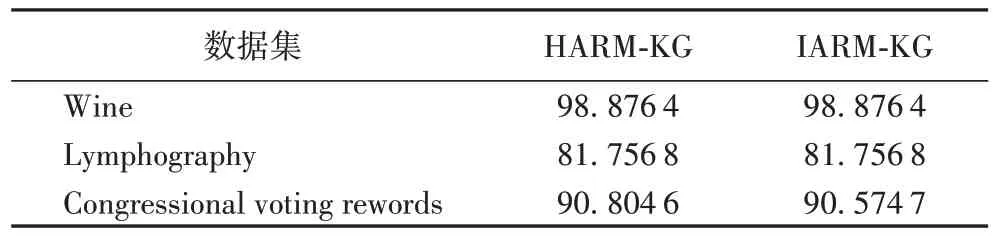
表4 两种方法的分类精度比较 单位：%Tab.4 Comparison of classification accuracy of two methods unit：%

5 结语

本文使用知识粒度来度量集值决策信息系统中的属性重要度，并在此基础上构建了属性集增加条件下的基于知识粒度的增量式属性约简方法。为了证实所构建的增量式约简方法的有效性和约简结果的准确性，借助于Matlab 编程平台上对UCI 上选取的3 组数据集进行了实验验证。从实验结果可得出，当集值决策信息系统中的属性集增加时，本文方法能够高效率地更新属性约简。但是本文只考虑了集值决策信息系统中属性集发生变化的情况，未来研究工作的重点是当有多个对象添加或删除的情况下，设计基于知识粒度的增量式属性约简方法。