数值分析课程中融入分数阶微积分的探索

陈安 农丽娟 谢海

摘  要：分数阶微积分是当前计算数学的研究热点之一，如何将这一科学研究融合到数值分析课程教学中，这个问题值得深入思考。文章首先介绍科教融合的背景，然后探讨数值分析课程教学中融入分数阶微积分科学研究问题的意义，最后通过具体的例子探讨其对人才培养的可行性。

关键词：分数阶微积分;数值分析;科教融合;人才培养

中图分类号：G640 文献标志码：A          文章编号：2096-000X（2022）04-0096-04

Abstract： Fractional calculus is one of the current research hotspots in computational mathematics. How to integrate this scientific research into the teaching of numerical analysis courses is worthy of in-depth consideration. In this paper， we firstly introduce the background of the integration of science and education， and then discuss the significance of integrating the scientific research of fractional calculus into the teaching of numerical analysis courses， and finally explore its feasibility for talent training through specific examples.

Keywords： fractional calculus; numerical analysis; integration of science and education; talent training

分数阶微积分近些年来受到了科学与工程领域的极大关注，是计算数学的研究热点之一。这是因为它能够很好地刻画自然界的非局部现象，比如分形材料中的热扩散、细胞膜中的蛋白质传输以及材料的粘弹性等。由于分数阶模型的解常常不易得到，因此涌现了非常丰富的数值求解方法以及相应的数值理论研究。

数值分析课程在高等学校教学中扮演着非常重要的角色，是信息与计算科学专业的专业核心课程。传统的教学方法一般仅关注形式的推导，且教学内容与现代科学技术的发展现状来看已略显不足。因此有必要结合分数阶微积分这一前沿科学研究来对数值分析的教学内容进行拓展。

最近，《教育部关于加强新时代教育科学研究工作的意见》文件中指出：增强科研成果转化意识，引导鼓励开展政策咨询类、舆论引导类、实践应用类研究，推动教育科研成果转化为教案、决策、制度和舆论[1]。因此，这为我们科教融合提供了很好的政策指导。此外，尽管目前高校的教育改革发展有了显著的进步，但是仍存在着一些不同的问题。在传统观念中，人们普遍认为教学是人才培养的主体，使得科学研究的育人职能、教学的学术性被严重削弱，从而从本质上背离了现代大学的育人理念[2]。如何在具体课程中融入科学研究值得我们深入思考。

本文讨论的分数阶微积分是当前的科学研究热点，一些学者已尝试将其应用到高等数学的教学当中[3]。因此在本文中，我们继续结合数值分析这门具体课程，以分数阶微积分的科学研究为例，探讨两者融合的意义，并以实例来说明融合的可行性。

一、数值分析课程中科教融合的意义

下面我们分两点探讨数值分析课程中融入科学研究，尤其是分数阶微积分科学研究的意义。

（一）丰富学生的专业知识体系，培养学生的创新能力

人才培养是高校永恒的主题，教学、科研、服务、文化都是人才培养的重要方式和途径[2]。而科学研究本身就具有育人性，这样使得在人才培养模式的途径上更为丰富。数值分析是信息与计算科学专业的一门专业核心课程，它扮演的角色非常重要，因此不能用传统的教学模式进行教学，而应迎合时代发展的潮流，顺势结合科学研究，这样才能丰富学生的专业知识体系，促进学生对科学问题兴趣的增加。

分数阶微积分是一个很好的科学研究材料。由于它是整数阶微积分的推广，因此学生更容易接受。另一方面也正由于是传统微积分的推广，使得它散发着科学研究的气息，从而学生可以在一些简单问题上大有作为，进而培养学生的创新能力。比如在常微分方程数值解法的教学中，可以适当穿插分数阶常微分方程的数值解法。从中我们可以看到后者与前者有相对应的求解方法，比如预估校正法等。这样一来，可使学生的兴趣得以激发，并加强了自身学习能力的信心。再进一步，可稍微修改下方程参数，让学生自由探索，培养学生的创新能力。

（二）提高教师的专业素质水平，促进课程思政的有机结合

适应教育改革发展和学科建设需要，坚持吸收借鉴和创新相结合，综合运用各种研究方法，创新教育科研范式，不断提升教育科研质量[1]。可以看到，要使得在教学过程中融入科学研究，首先得保证教师的专业素质水平，这样才能促进学科的良性发展。这是因为只有对科学问题有深层次的认识，才能够自然地将科学问题融入到教学当中，从而使得科研成果的转化具有普遍性。这不仅提高了教学效果，也使得教师在交流分享过程中提升对问题的认识，进而对学科的良性發展起到很好的促进作用。

分数阶微积分这一领域正在蓬勃发展中，教授数值分析课程的主讲老师一般也是计算数学专业出身，因此可以通过与同行交流或自学方式提高自身的专业水平。此外，我们也可以从数值分析与分数阶微积分的发展历史，深挖专业知识中所蕴含的思想价值，从而增加课程的知识性与人文性，进而培养学生探索未知和追求真理的使命感，这也恰恰是课程的思政元素之一[4]。以数值分析中数值积分为例。我们可根据推导的积分公式讲解分数阶积分的逼近公式，并通过介绍我国在对分数阶积分数值计算研究的发展历程，让学生感受到科学研究的严谨性。

二、数值分析课程中科教融合的实践

在这一部分我们以3个具体例子说明分数阶微积分在教学实践中的可行性。

（一）复合求积公式

在讲解完复合求积公式的时候，以Caputo分数阶导数的逼近公式推导为例，通过对Caputo分数阶导数的离散进行知识扩展，培养学生创新精神。为了讨论方便，先介绍Caputo分数阶导数的定义。

定义：函数f（t）的α 阶 Caputo分数阶导数的定义为：

可以看出， Caputo分数阶导数在分数阶α 趋于整数 n 时，它将重现传统的n阶整数阶导数。从Caputo分数阶导数的定义出发，可介绍与一般积分做类比，强调分数阶导数只不过是比积函数多了一个用于刻画物质物理特性的核函数tn-α-1而已。另一方面，也可以在一定程度上将该Caputo分数阶导数的定义看成核函数与导函数f（n）（t）的区间[a，t]的卷积（这里，我们已将定义中的系数放在核函数中），从而为下一步拓展做好铺垫。

为讨论方便，现只考虑n=1的情形，其他情形可类似推导。现要求函数f（x）的Caputo分数阶导数在t=T>0处的近似值，因此可以利用复合求积公式的离散思想。首先将区间进行等距划分，然后在每个小区间进行考虑。不同于数值分析课本中的介绍，这里需要学生有创新意识。如果只针对被积函数中的f（t）进行线性插值，则可将所求的逼近公式用离散结点处的函数值加权求和后得到，这种方式很自然地得到了Caputo分数阶导数的逼近公式。此时，这里的逼近公式，也称为L1逼近公式，它在分数阶数值领域研究得较为透彻，已有一系列的成果[5]。在这一点上，可适当介绍我国学者对它的研究历史，从而激发学生的钻研精神。

下面给出具体的推导过程，以说明Caputo分数阶导数的逼近公式蕴含着最基本的复合求积和插值近似的思想。为此，取正整数N， 令步长为 τ=（T-a）/N， 则节点tk=a+τk，k=0，1，…，N。在每个小区间[tk，tk+1]中对函数f（t）利用小区间两个端点的函数值信息做线性插值：f（t）=f（tk）+f（tk+1），于是CDf（t） 在tn处的近似值可由下面推导得到。

其中权系数

wm=（m1-α-（m-1）1-α），m=1，2，…

从中我们可以看到，在得到Caputo分数阶导数的推导过程中运用到了函数插值内容，因此这相当于将不同的知识点融合在一个科学研究问题的求解中。这不仅使得学生能知晓数值积分的应用场景，也能够对以前所学的内容融会贯通。此外，我们这时也应该强调，所得到的逼近公式为当前分数阶微积分领域使用最多的公式，常常应用在时间分数阶反常扩散模型的数值离散中，从而提高学生的研究兴趣。

更进一步地，我们可以布置开放性的作业或课题，例如我们布置这样的开放性作业：“假设用更高阶的插值公式代替上面的线性插值，结果又会是怎样？请同学们推导相应的逼近公式，并编程验证结果。”从而使得选择的科研问题与教学内容更为切合，激发学生的求知欲，达到育人目的。

（二）欧拉法

在介绍常微分方程初值问题的数值解法時，可适当添加分数阶常微分方程的数值离散。以下面的分数阶常微分方程初始值问题为例：

其中0<α<1， 初始值为：u（0）=v。它等价于下面的Volterrra积分方程[5]：

当然，这个等价关系的推导需要利用到分数阶微积分的一些基本恒等式，在课堂上直接引入等价的Volterra积分方程即可，从而避免过多的细节对教学目的造成影响。这样便将问题转化为对Volterra积分方程的求解。

回忆常微分方程中可将其转化为积分方程求解，如对方程：u′（t）=f（t，u（t））左右两端同时在小区间[tk，tk+1]积分，整理后可得到：u（tk+1）=u（tk）+f（t，u（t））dt，从而欧拉法可看成是对积分方程的右端积分项应用左矩形公式而得到。在这一角度下，我们可借助欧拉法的思想，将Volterra方程右端的积分项先等距剖分，然后在每个小区间[tk，tk+1]中，利用小区间左端点的函数值信息f（tk，u（tk））近似f（t，u（t）），从而可得到Volterra积分方程的离散格式。我们这里给出具体的推导过程。首先在节点t=tn处考虑Volterra 积分方程：

其中系数

记u（t）在节点t=tn处的近似值为un，那么我们可得到用于近似求解Volterra积分方程的数值公式：

通过将整数阶常微分方程中的欧拉法与分数阶常微分方程做比较，让学生更加深刻理解数值离散的本质思想，从而扩展学生的数学思维。类似第一个例子，也可以让学生在这个基础上布置些开放性问题，如：“如果在小区间[tk，tk+1]中应用右端点的函数值信息f（tk+1，u（tk+1））近似f（t，u（t）），那么得到的数值格式是什么？再进一步，如果利用小区间左右两个端点的函数值信息来近似，得到的数值格式又是什么？如果得到的格式是隐格式，那可否利用预估校正的思想设计对应的有效格式？”这些问题都是基于最基本的常微分方程和数值积分的离散方法，这样既丰富学生的专业知识，又培养学生的钻研精神。

（三）数值演示相关

在充分挖掘分数阶微积分在数值分析中的教学材料时，除了强调在离散格式的可类比性推导外，还可适当添加具体的实例在课堂上演示。比如，为了让学生更直观地观察到Caputo分数阶导数近似解与传统整数阶的联系，这里举两个简单的例子。

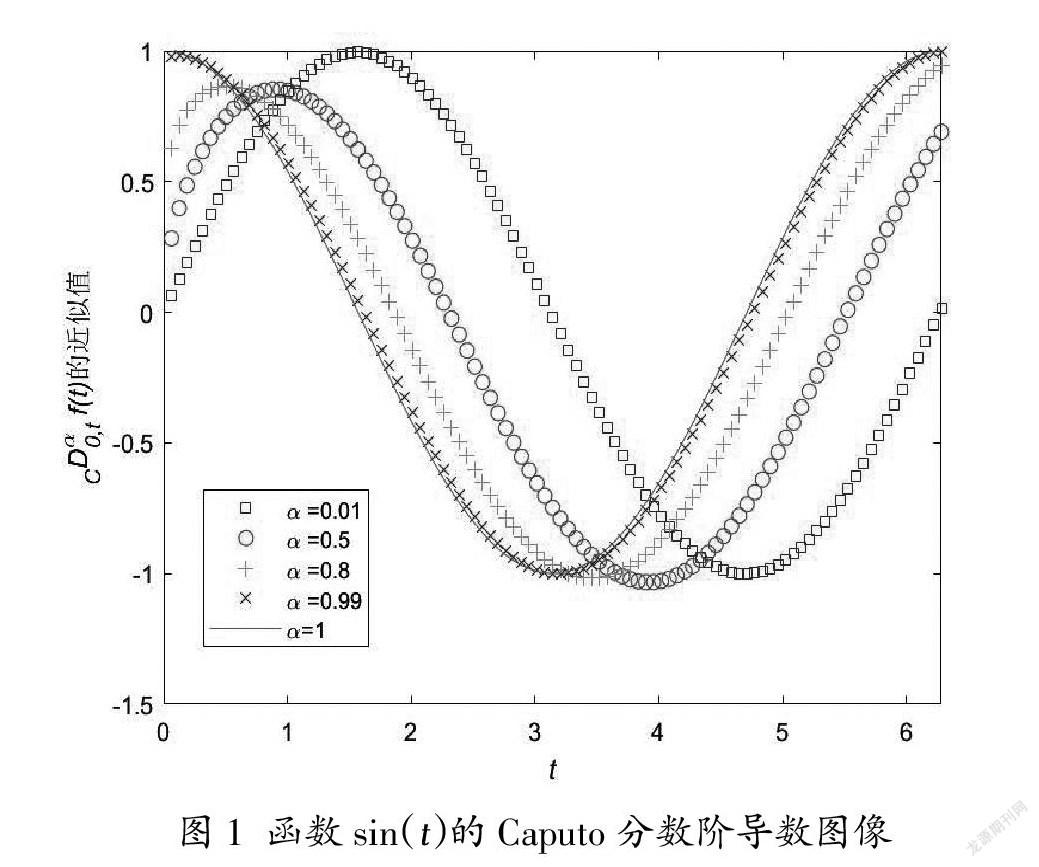
首先令f（t）=sin（t），则可以利用上面推导得到的L1逼近格式计算相应的Caputo分数阶导数近似值。得到的图像如图1所示。

为方便读者实现，这里我们提供如下的Matlab代码：

T= 2*pi; %求解区间（0，T]

f = @（t）sin（t）; %将要计算Caputo分数阶导数的函数

Df = @（t）cos（t）;%函数f 的一阶导数

alpha = [0.01， 0.5， 0.8， .99]; %计算的分数阶

line_stype = {'s'， 'o'， '+'， 'x'}; %设置线段类型

Nt = 100; tau = T/Nt; %剖分节点的个数以及时间步长

tn = （1∶Nt）*tau; %剖分的节点

for k=1∶length（alpha）%计算不同alpha下的近似解

legend_str{k} = strcat（'＼alpha = '，num2str（alpha（k）））;

numeru = zeros（Nt， 1）; %记录每个节点上的Caputo分数阶导数近似值

for j=1∶length（tn）%遍历每个节点

%计算权系数

weight = （（j∶-1∶1）.^（1-alpha（k）） ...

- （（j-1）∶-1∶0）.^（1-alpha（k））） / gamma（2-alpha（k））;

diff = f（tau*（1∶j）） - f（tau*（0∶（j-1）））;

numeru（j） = sum（weight.*diff） / tau^alpha（k）;

end

plot（tau*（1∶Nt）， numeru， line_stype{k}）;

hold on;

end

plot（tau*（1∶Nt）， Df（tau*（1∶Nt）））; %绘制一阶导数的图像

legend_str{length（alpha）+1} = '＼alpha=1';

legend（legend_str）; xlim（[0，2*pi]）; %添加描述性標签

xlabel（'t'）; ylabel（'_CD_{0，t}^＼alpha f（t）的近似值'）;

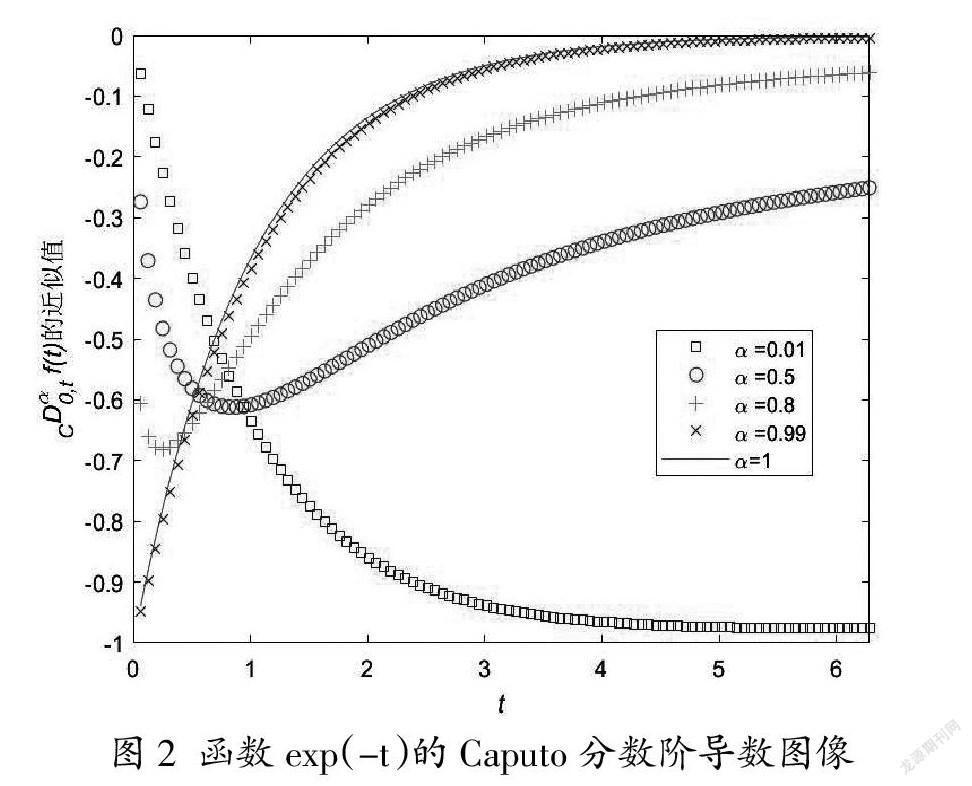
接着令f（t）=exp（-t）， 同样地，应用L1逼近格式计算相应的Caputo分数阶导数近似值的图像如图2所示。

此外，我们还可以绘制其他基本函数的分数阶导数图像。从得到的图1-2看出，当分数阶趋于1时，分数阶导数重现传统导数，而相应的L1逼近格式退化为求解一阶导数的向后欧拉差分。因此，通过直观的图像演示，让学生对分数阶微积分有更为深刻的印象，从而培养学生学习数值分析课程的兴趣，进一步提高课程学习的兴趣。

三、结论

本文以分数阶微积分为例，探讨了在数值分析课程中融入科学研究的意义，并利用3个例子说明了科教融合是可行的。在课程教学中融入科学研究已成为高等教育改革发展的必然趋势，在接下来的教学与科研工作中我们将不断探索，使得分数阶微积分在数值分析教学中的典型例子更为丰富，理论体系结构更为完善。

参考文献：

[1]教育部关于加强新时代教育科学研究工作的意见[J].中国高等教育评估，2019，30（4）：70-73.

[2]周光礼，马海泉.科教融合：高等教育理念的变革与创新[J].中国高教研究，2012（8）：15-23.

[3]陈安.浅谈分数阶微积分在高等数学教学中的应用[J].高教学刊，2019（17）：116-119.

[4]余江涛，王文起，徐晏清.专业教师实践“课程思政”的逻辑及其要领——以理工科课程为例[J].学校党建与思想教育，2018（1）：64-66.

[5]孙志忠，高广花.分数阶微分方程的有限差分方法[M].北京：科学出版社，2015.