基于BP神经网络的输电线路电场屏蔽效果预测*
于利佳, 田 瑾, 吴 飞, 龚 利
(1.上海工程技术大学 电子电气工程学院,上海201620; 2.华东师范大学 城市与区域科学学院,上海 200062)
0 引 言
如今,输电线路产生的电磁环境对长期生活在线路周围的居民产生了极大的影响。电磁环境影响参数主要包括工频电场、工频磁场、无线电干扰和可听噪声四个方面,其中工频电场的影响成为公众最为关注的问题之一。
目前,电磁场计算的方法主要有模拟电荷法[1,2]、矩量法[3]、有限元法[4]等,电磁场预测用到的模型主要有灰色预测[5]和人工神经网络(artificial neural network,ANN)[6,7]等。作为计算超高压输电线路电场的主要方法,由于有限元法计算较模拟电荷准确,但此类方法通常需要建立模型后反复修改参数进行计算,可利用有限元法计算得到部分屏蔽线位置电场强度值作为训练值。对于未知位置对应的屏蔽效果,利用反向传播(back propagation,BP)神经网络进行预测,因为其操作简单、高度自学习和自适应特性,使其拥有较高预测非线性相关问题能力。
本文提出采用BP神经网络的输电线路电场屏蔽效果的预测模型,以500 kV同塔双回输电线路为例,借助有限元软件Ansoft Maxwell搭建输电线路模型,计算出从屏蔽线数量、架设高度以及水平位置不同角度优化屏蔽效果的电场强度值,在此基础上,通过神经网络将预测值与真实值进行对比验证模型的可行性和准确性,结果可为超高压输电线路电场环境优化及建设提供参考依据。
1 神经网络模型
1.1 人工神经网络
人工神经网络是由大量神经元广泛相互联结而成的非线性的、动态的复杂网络信息处理系统。起源于现代神经学研究成果,能够模拟人脑的基本功能。它能够从累积的案例中学习知识,将各种定量或定性的因素尽可能地作为变量加以输出,建立因素与结论间的非线性映射,采用自适应模式识别的方法来完成预测工作[8]。
神经元模型如图1所示。
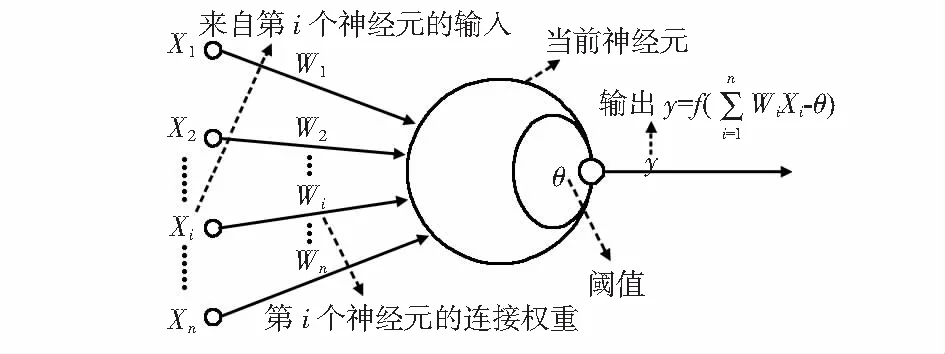
图1 神经元模型
图1中显示,n个神经元通过连接权重将信息整合到神经元汇总,然后和阈值作比较,最终通过相关激活函数输出预测值。常用的激活函数有Sigmoid函数
Sigmoid=1/(1+e-x)
(1)
1.2 BP神经网络
在人工神经网络中,前馈BP神经网络使用的最多。通常BP神经网络由三层结构组成,如图2所示。
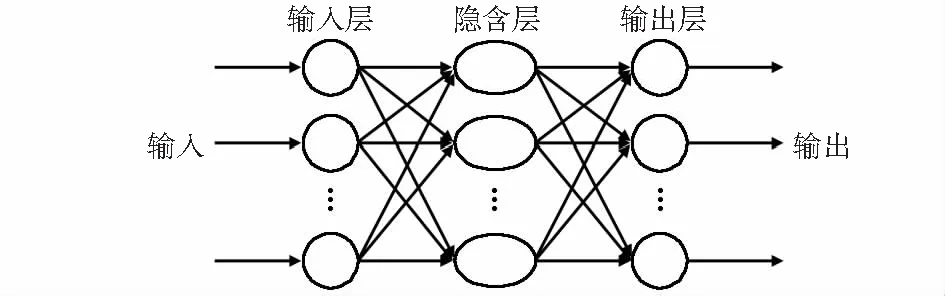
图2 多层前馈神经网络结构
左右各层神经元由连接权值连接,上下并无连接。BP神经网络是有导师神经网络,在初期会给一个学习模式,最终神经元学习该模式进行传播,输出预测结果。隐含层单元误差和下降梯度是否需要计算且通过修改权重与阈值来重新学习,主要取决于实际输出和期望输出之间的误差是否满足精度要求,通过迭代操作可使输出值结果更加准确[9]。具体BP神经网络学习算法流程如图3所示。
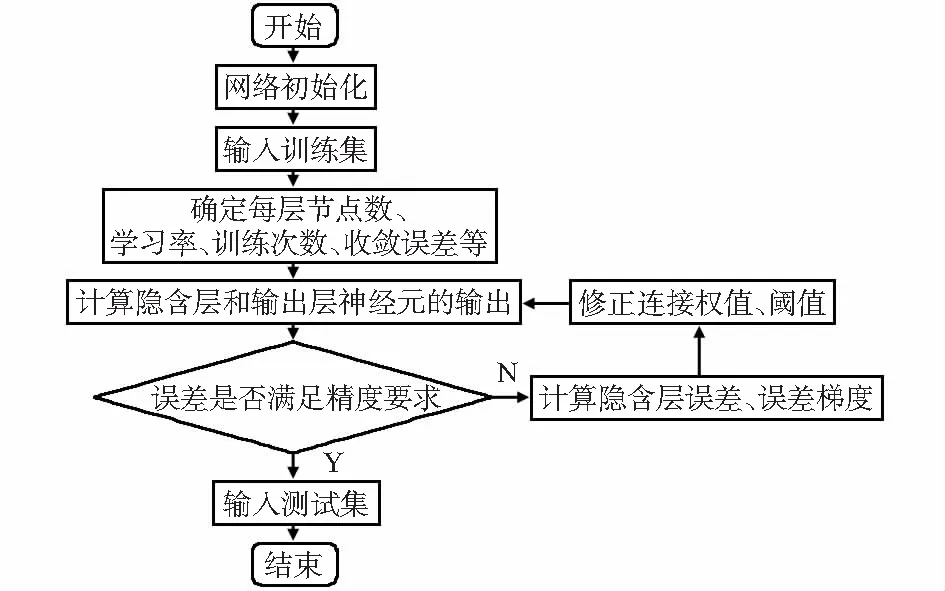
图3 BP神经网络模型算法流程
2 输电线路屏蔽模型
国内外针对输电线路电磁场研究表明[10],工频电场强度除了随导线架设位置、结构等参数变化外,还可以通过架设屏蔽线降低工频电场强度。因此,为研究线下工频电场屏蔽效果,本文以500 kV同塔双回输电线路为对象分析架设屏蔽线对线下1.5 m处电场的影响,其中屏蔽线型号为LGJ—240/30,如图4所示,h为屏蔽线的对地高度,d为两侧屏蔽线到线路中心的水平距离。通过改变三根屏蔽线的位置,可以得到相应的工频电场强度值。
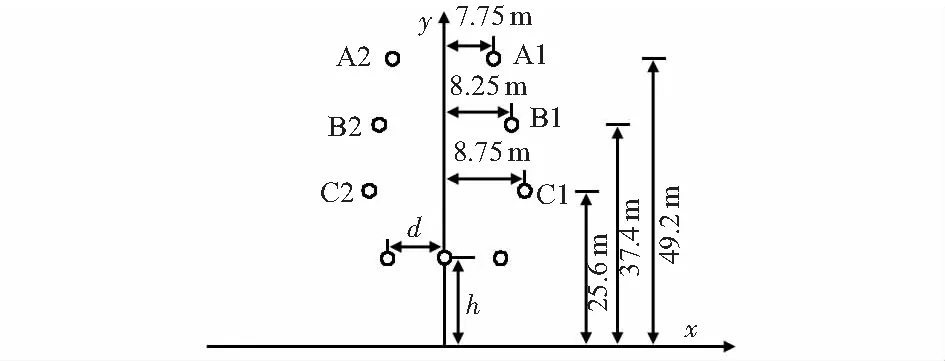
图4 架设屏蔽线计算模型
3 基于BP神经网络的电场强度预测模型
3.1 电场强度预测模型的构建
实际生活中,针对未建好的输电线路,通常需要提前进行预测,而针对已建好的输电线路,通常处于山区或闹市区,不易测量或成本过高[11]。因此,本文提出建立合理准确的电场强度屏蔽线优化预测模型。
由文献[12,13]可知,输电线路线下电场强度与屏蔽线架设高度和水平位置均有关,但这种关系是非线性的,不易通过数学公式直接计算得到。因此,本文将部分已知的输电线路屏蔽线对地高度、水平位置和相对应的电场强度数据作为训练集,将其他已知的屏蔽线对地高度、水平位置作为测试集数据,通过将预测结果和电场强度真实值进行对比建立BP神经网络模型进行验证。
基于BP神经网络电场强度预测模型具体步骤如下:
1)建立训练集:本文对500 kV同塔双回输电线路屏蔽线数据进行整理,取屏蔽线参数不同的44组数据(包括:屏蔽线对地高度、水平距离和相对应的电场强度)作为训练集输入。
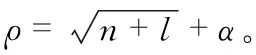
3)建立测试集:将500 kV同塔双回输电线路屏蔽线数据进行整理,取屏蔽线参数不同的12组数据(包括:屏蔽线对地高度、水平距离和相对应的电场强度)作为测试集输入。
3.2 电场强度预测结果分析
通过改变500 kV同塔双回输电线路架设屏蔽线对地高度、水平距离,得到44组不同数据工频电场强度值。
通过MATLAB对表中数据采用BP神经网络训练,仿真过程如图5所示。
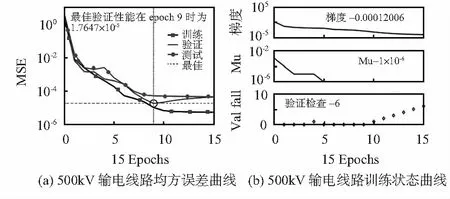
图5 500 kV输电线路均方误差与训练状态曲线
神经网络在训练数据中,会将数据按照一定比例分为训练集(training set)、验证集(validation set)和测试集(testing set),以便模型的预测准确性。其中训练集主要是对数据样本进行模拟拟合,验证集负责寻找最优的网络深度,测试集负责最终模型的泛化能力,即预测准确性。
本文训练算法选取的是莱文贝格—马夸特法(Levenberg-Marquardt algorithm),该算法可结合高斯—牛顿算法以及梯度下降法的优点,并对不足之处进行改善。如图6所示,Train,Validation和Test曲线分别表示训练样本、验证样本和测试样本。模型迭代次数为9时,验证样本的均方误差(mean squared error,MSE),即均方误差最低为0.000 017 6,性能最好,经过更多训练阶段后,随着网络过度拟合训练数据,验证误差连续迭代6代不减反增,因此模型在第15次迭代后结束。 经过分析可知,该模型训练样本相关系数R=0.999 94,验证样本相关系数R=0.999 92,测试样本相关系数为R=0.999 51,样本总的相关系数为R=0.999 88,整体模型训练效果较好。
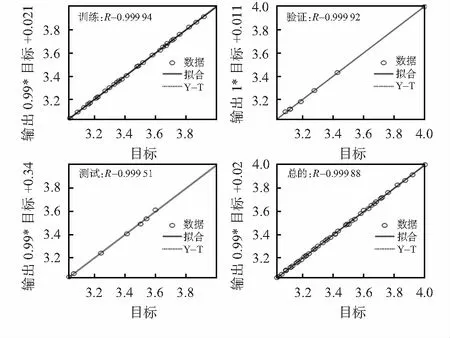
图6 500 kV输电线路回归
本文将12组500 kV同塔双回输电线路架设屏蔽线对地高度、水平距离数据作为预测模型的输入集建立神经网络预测模型,并将预测结果和真实值进行对比。
将工频电场真实值和模型预测值作出对比图,如图7所示,基于BP神经网络建立得训练模型对输电线路屏蔽效果进行预测,预测值与真实值最大误差为0.6 %,具有较好的预测效果。
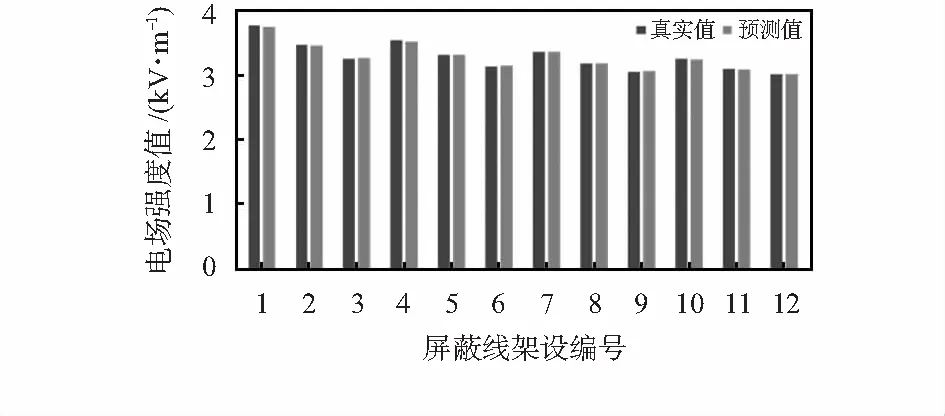
图7 500 kV输电线路电场强度对比
4 结 论
本文首先建立输电线路屏蔽线模型,从屏蔽线数量、架设高度以及水平位置不同角度研究优化屏蔽效果,得到部分不同位置下电场强度值,并利用BP神经网络预测未知位置下电场强度值,经对比结果表明,预测值与真实值误差很小,具有较好的预测效果。

