基于深度强化学习的大规模电动汽车充换电负荷优化调度

刘敦楠，王玲湘，汪伟业，李 华，王 文，刘明光

（1. 华北电力大学经济与管理学院，北京市 102206；2. 国网电动汽车服务有限公司，北京市 100053）

0 引言

2020 年9 月，国家发展改革委发布《关于扩大战略性新兴产业投资培育壮大新增长点增长极的指导意见》［1］，鼓励智能汽车与智慧城市协同发展。电动汽车（EV）作为重要的灵活性可调资源，能够与多种能源协同调度［2-3］，为电力系统的经济可靠运行提供支撑［4-5］。然而，在电动汽车灵活性资源的实际应用过程中也面临着一些重要问题，其中电动汽车可调资源分析［6-7］和智能协调调度方法设计［8-9］是两项关键问题。

目前，电动汽车灵活性负荷的研究通常围绕电动汽车充放电的优化调度展开。例如，文献［10］采用分群优化的方法控制电动汽车充放电过程，从而实现电动汽车对电网负荷的调节；文献［11］通过控制规模化电动汽车的充放电，实现电动汽车与风电、火电的协同优化；文献［12］基于用户充电距离等因素对用户满意度的影响，对电动汽车入网的可调性进行判断。但上述研究都是直接对电动汽车的优化调度过程进行研究，未结合用户可调性识别，也并未考虑到决策主体是电动汽车聚合商（electric vehicle aggregator，EVA），而EVA 的优化调度过程中还具有另一种可调节资源——换电资源，随着充换电一体化建设进程的推进，换电负荷将在聚合调度中发挥重要的作用［13-15］。

在电动汽车智能协调调度方法的研究中，广泛使用的算法有交替方向乘子法（alternating direction method of multipliers，ADMM）［16-17］、拟 牛 顿 法（BFGS）、启发式算法［18-19］、约束优化求解算法［20］、人工智能算法［21］等。其中，ADMM、BFGS、启发式算法和约束优化求解算法都是基于全局环境状态对现有决策变量进行求解，具有计算复杂度高、决策空间大、容易陷入局部最优、无法区分个体调度方案、环境数据需实时更新等缺陷，无法求解大规模电动汽车的实时调度问题。而强化学习等人工智能算法通过神经网络对大数据的拟合能力，避免了传统算法重复的高复杂度的计算［22］，可以在未知全局用户接入的情况下对单个用户做出合理的全局较优的调度安排，解决了传统算法对数据的实时依赖性高的缺陷，具有优化效果好、鲁棒性强、计算效率高的特征，适用于大规模电动汽车实时优化调度的求解。

基于上述研究内容，考虑目前充换电一体化建设进程，本文首先从EVA 的角度设计了电动汽车充换电过程的联合运行框架；进而，考虑用户参与电动汽车负荷优化调度意愿和可调节潜力，设计考虑多重用户特征的可调性识别模型；然后，提出电动汽车充换电负荷的实时优化调度模型；最后，基于SAC（soft actor-critic）强化学习算法对充换电负荷进行实时优化调度，并采用真实数据对所提模型的有效性进行验证。

1 电动汽车充换电站联合运行框架

电动汽车充换电负荷联合优化调度的基本框架如图1 所示，其中EVB 表示换电站电池。

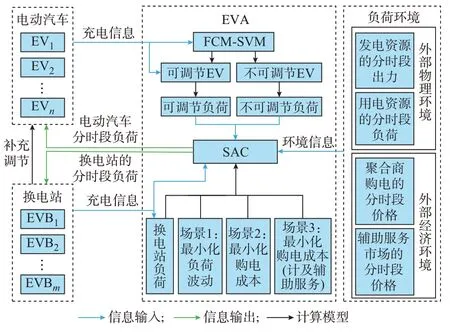
图1 充电桩与换电站联合优化调度框架Fig.1 Joint optimal scheduling framework of charging pile and battery swapping station

本文所提优化调度框架主要从EVA 的角度出发，考虑充电桩与换电站两大资源主体进行资源优化调度，其特征具体如下:

1）在EVA 内外部关系方面，调度框架包括EVA 内部资源、EVA 和外部电力系统，EVA 通过聚合调度内部充换电负荷实时响应外部电力系统运行的变化情况。

2）EVA 内部调度方法主要包括3 个阶段:（1）充换电负荷信息录入；（2）可调节电动汽车负荷识别；（3）电动汽车充换电负荷协调调度。

3）EVA 与外部环境的协调主要设置3 种典型场景:场景1 是EVA 作为微网或者相关联合体中的一部分进行调度，以平抑负荷波动；场景2 是EVA作为独立个体，仅接受分时段价格的引导，调节负荷以实现最小充电成本；场景3 是EVA 作为参与辅助服务的市场主体，兼顾辅助服务市场效益与购电成本进行调度，以实现EVA 经济性最优。

据此研究电动汽车充换电负荷的实时优化调度策略，并分析其对于电力系统经济可靠运行的贡献。

2 电动汽车充电站调度策略

2.1 可调节电动汽车用户识别

电动汽车接入充电设备后具有负荷调节的可能性。因此，本文考虑一种基于模糊C均值（fuzzyCmeans，FCM）可调隶属关系确认与支持向量机（support vector machine，SVM）智能识别的电动汽车用户可调性识别方法，以智能识别可调节电动汽车和不可调节电动汽车。

影响电动汽车响应能力的主要因素包括充电功率、荷电状态（SOC）、充电时长（达到理想荷电状态的最短时长）和接入时长（入网到离网时间）。而用户行为偏好则通过车型、电池容量、日均电力需求、日均入网时长、用户积分/优惠券使用情况等特征参数来进行反映。基于此，设置电动汽车充电可调性特征元组如式（1）所示。

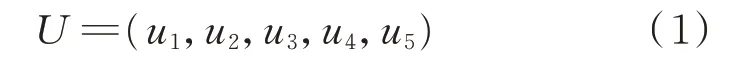
式中:u1为车型特征参数；u2为电池容量特征参数；u3为电力需求特征参数；u4为用户接入时长特征参数；u5为用户激励特征参数，为0-1 变量。对应的计算方式如式（2）所示。

采用FCM 对典型电动汽车充电可调性特征元组的样本进行聚类分析，可以得到有意愿参与响应与无意愿参与响应的聚类中心。聚类过程中目标函数见式（3），约束条件见式（4）。

式中:W为样本总数；w为样本数标识；v为类别数；Uw为具有5 维特征的样本；Zv为具有5 维特征的第v簇的中心；αw，v为样本Uw属于第v类的隶属度，单个样本Uw对每个簇的隶属度之和为1；γ为隶属度因子；‖Uw-Zv‖表示负荷样本到聚类中心的欧氏距离。

利用式（3）和式（4）可推导出隶属度αw，v的计算式（5）和簇中心Zv的计算式（6），推导过程见附录A。

式中:k为类别标识，实际含义与v一致。

迭代至满足式（7）时终止。

式中:n为迭代次数；ε为误差阈值。

得到簇中心分别如式（8）与式（9）所示。

据此，定义电动汽车参与响应隶属度与不参与响应隶属度分别如式（10）与式（11）所示。

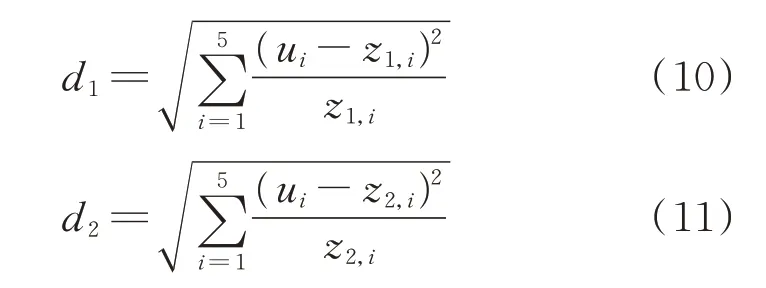
式 中:z1，i和z2，i分 别 表 示 簇 中 心Z1和Z2的 第i个元素。

进而，以样本电动汽车用户充电可调性特征元组作为输入，以样本电动汽车的实际可调属性作为输出，即可构造映射关系。采用典型数据训练SVM后［23-24］，即可利用训练后的FCM-SVM 模型对电动汽车接入情况进行实时可调性判断。

2.2 不可调节与可调节负荷

基于可调性判断结果可对电动汽车的可调节负荷和不可调节负荷进行测算。

2.2.1 不可调节负荷

不可调节负荷的计算方法如式（12）所示。

式 中:Qu，t为t时 段 的 不 可 调 节 负 荷；Eu，s，t为t时 段 第s辆不可调节电动汽车的充电电量；M为不可调节电动汽车集合。

对于不可调节电动汽车来说，其充电过程具有如式（13）和式（14）所示特征。

1）电量特征

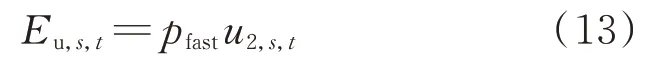
式 中:pfast为 最 大 充 电 功 率；u2，s，t为t时 段 第s辆 不 可调节电动汽车的充电时长。

2）功率特征

不可调节电动汽车的充电功率按照电动汽车车主设置或者最大充电功率充电。

3）充电时间特征

不可调节电动汽车的充电时长如式（14）所示，接入时长由车主意愿决定。

式中:Eneedu，s为第s辆不可调节电动汽车的最小充电需求；Ts，in为第s辆不可调节电动汽车的充电总时长。

2.2.2 可调节负荷可调节负荷的计算方法如式（15）所示。

式 中:Qc，t为t时 段 的 可 调 节 负 荷；Ec，p，t为t时 段 第p辆可调节电动汽车的充电电量；N为可调节电动汽车集合。

对于可调节电动汽车来说，其充电过程具有如式（16）至式（18）所示特征。

1）充电电量特征

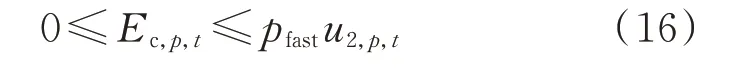
式 中:u2，p，t为t时 段 第p辆 可 调 节 电 动 汽 车 的 充 电时长。

2）功率特征

式 中:pc，p，t为t时 段 第p辆 可 调 节 电 动 汽 车 的 充 电功率。

3）电动汽车电量特征:

2.3 可调节电动汽车的最优化调度模型

基于用户的充电需求与用户特征元组U，可以对接入的电动汽车进行实时优化调度。据此，设置根据电动汽车在3 种典型场景下的聚合优化调度目标函数。

1）场景1

基于电动汽车聚合平抑负荷波动的优化调度目标函数如式（19）所示。该场景下可以基于现有负荷基线（外部物理环境总负荷与不可调节负荷的和），每加入1 辆电动汽车，为其设计最小化负荷波动的电动汽车充电方案。

式中:Qload，t为t时段不计电动汽车的系统负荷值；E′c，p，t为调节后的电动汽车在t时段的负荷值；Qave为系统所有负荷的均值，其计算式见式（20）。

2）场景2

基于EVA 购电成本最低的优化调度目标函数见式（21）。基于原有负荷曲线的充电成本，每加入1 辆电动汽车，为其设计最小化充电成本的电动汽车充电方案。

式 中:pa，t为 电 力 市 场 在t时 段 的 购 电 价 格；Qtar，t为 电动汽车在t时段的原始负荷值。

3）场景3

考虑辅助服务市场的优化调度目标函数见式（22），每加入1 辆电动汽车，对其设计最小化充电成本的充电方案。

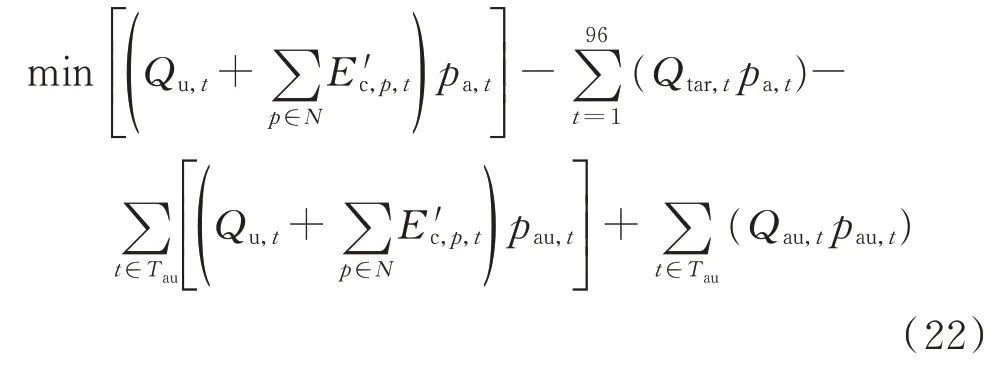
式中:Tau为辅助服务市场的开市时段；pau，t为t时段的辅助服务市场价格；Qau，t为t时段的电动汽车参与辅助服务市场的负荷基线。

3 电动汽车换电站调度策略

3.1 换电站行为约束

换电站充换电过程中电池总量保持不变。因此，令换电站内所有电池具有编号o，将换电站内换出电池编号赋予换入电池。

换电站总负荷计算如式（23）所示。

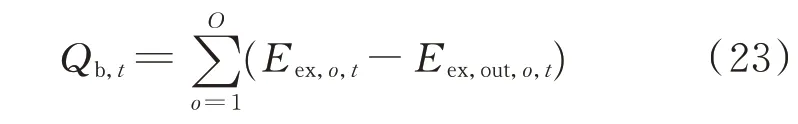
式中:Qb，t为t时 段换电站 的总负荷；Eex，o，t为t时 段第o组电池的充电电量；O为换电站电池总组数；Eex，out，o，t为t时 段 第o组 电 池 的 放 电 电 量。

换电站运行过程中，具有如式（24）至式（32）所示的特征约束。

1）电池的充电情况约束

式中:ωo为第o组电池是否接入充电机的标识；pmin和pmax分别为充电机的最小、最大充电功率；Δt为每时段的时长。

2）换电站电池放电约束

式 中:pmin，out和pmax，out分 别 为 充 电 机 的 最 小、最 大 放电 功 率；Cout，o，t为t时 段 第o组 电 池 的 放 电 成 本；Rout，o，t为t时 段 第o组 电 池 的 放 电 收 入。放 电 过 程 中的成本与收益计算式见附录B。

3）电池的接入情况约束

式中:I为换电站充电机总数。

4）电池电量约束

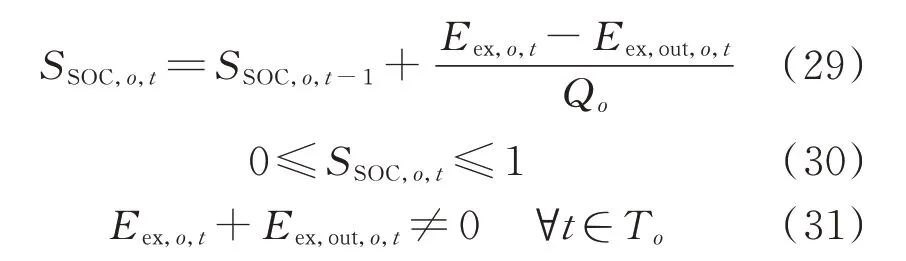
式 中:SSOC，o，t为t时 段 第o组 电 池 的SOC；Qo为 第o组电池的电池容量；To为第o组电池接入充电设备的总时间。式（30）保证电池充放电不超出电池容量约束；式（31）保证电池接入充电机过程中不造成资源浪费，未充满电的电池不离网。

5）换电站充放电池供应约束

式中:Cex，t为t时段换电站需完成的换电电池量；Bex，t为t时段换电站已有的满电电池量。

换电站充放电过程中具有满电的电池数量计算式如式（33）、式（34）所示。

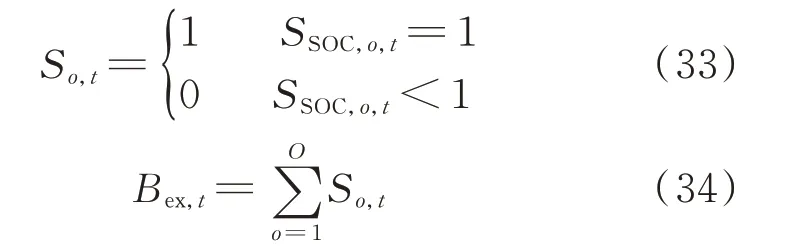
式中:So，t为t时段第o组电池是否满电的判断结果。

3.2 换电站优化调度模型

换电站通过更换电池来满足电动汽车电量需求，具有充放电灵活性较高、电池更换速度快的特点。换电站协调充电站进行优化调度时，考虑其容量规模相对较小［25-26］，将其作为一种补充资源协调充电站的充电过程，进一步优化负荷曲线。

对于场景1，其目标函数如式（35）所示。

式中:Q′ave为t时段加入换电站负荷后的负荷均值，其计算式如式（36）所示。

对于场景2，其优化调度函数如式（37）所示。

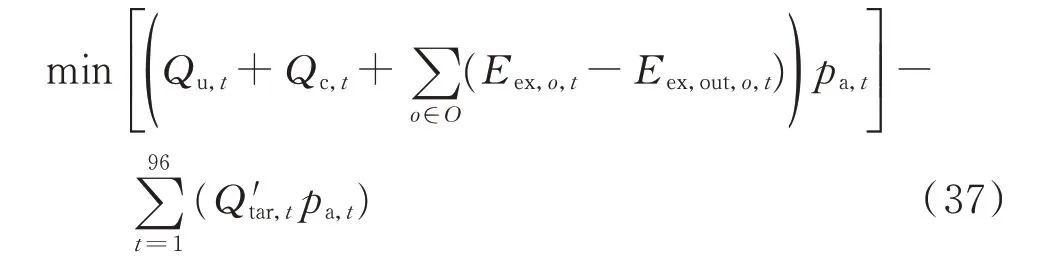
式中:Q′tar，t为加入换电站负荷后t时段的原始负荷值。

对于场景3，其优化调度函数如式（38）所示。

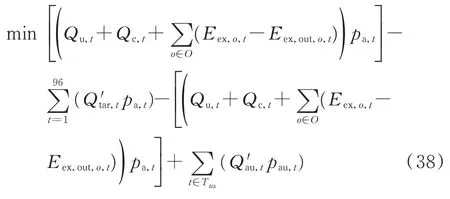
式中:Q′au，t为加入换电站负荷后的辅助服务市场的负荷基线。

4 基于SAC 强化学习的优化调度算法

SAC 算法是由Haarnoja 等人［27-28］提出的强化学习算法，通过引入最大熵鼓励策略，在提高算法的鲁棒性的同时加快了训练速度，能够在复杂的电力供需环境中为大规模电动汽车作出精准有效的调度决策。

4.1 SAC 目标函数

SAC 的目标函数要求策略在实现最大化累计回报的同时最大化策略熵，从而避免学习过程中的贪婪采样而陷入局部最优。据此，构建其目标函数如式（39）所示。

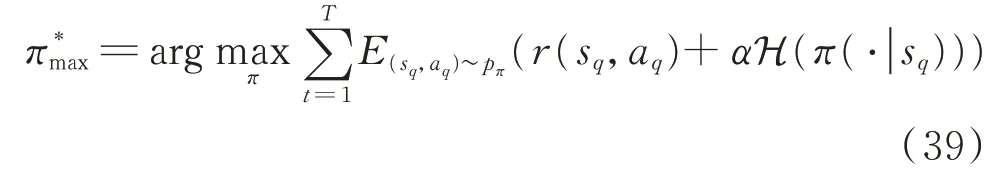
式中:E( · )为期望函数；π为策略；sq为第q辆电动汽车的状态空间（即系统基础负荷情况）；aq为第q辆电动汽车的动作空间（即充电情况）；r(sq，aq)为第q辆电动汽车的奖励函数，基于不同场景体现为不同的目标函数，如式（19）至式（22），是目标函数的相反 数；(sq，aq) ～pπ为 策 略π所 形 成 的 状 态-动 作 轨迹；α为温度项，决定了熵对于奖励的影响程度；H(π( ·|sq))为状态sq时的策略的熵项，其计算方法如式（40）所示。

4.2 SAC 迭代策略

强化学习过程中的价值函数Q(sq，aq)如式（41）所示，用于策略价值评估；贝尔曼backup 算子如式（42）所示，用于策略更新。

Q(sq，aq)=r(sq，aq)+γEst+1～p(Q(sq+1，aq+1)) （41）

TπQ(sq，aq)≜r(sq，aq)+γEst+1～p(V(sq+1)) （42）式中:Est+1～p为状态空间为st+1的期望函数；Tπ为策略π下的贝尔曼backup 算子；γ为奖励的折扣因子；V(sq+1)为状态sq+1的新值函数，其计算方法如式（43）所示。

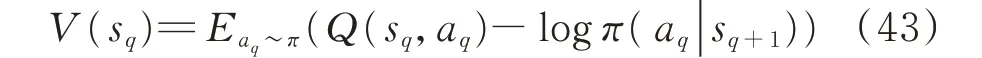
同时，有

式中:Qk为第k次计算时的价值函数。

将式（42）和式（44）不断进行迭代，即可实现式（45）。

4.3 SAC 策略更新

计算过程中的策略更新办法如式（46）所示。策略πold下的配分函数，用于归一化分布。

4.4 SAC 算法构建

SAC 算法需要构建神经网络，包括Q 值网络和策略网络。Q 值网络通过几层神经网络输出单值，策略网络输出一个高斯分布。该过程中神经网络会进行更新，Q 值网络参数具有如式（47）所示更新策略，策略网络参数具有如式（48）所示更新策略。

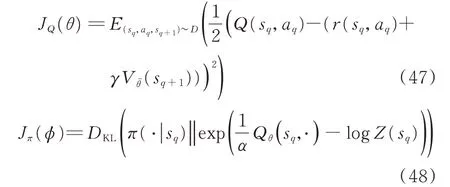
式中:θ为Q 值网络参数；φ为策略网络参数；Vθˉ和Qθ分别为代入Q 值网络参数后的新值函数和价值函数；Z(sq)为状态sq时的配分函数。

同时，前文提到的温度参数α是辅助最大化熵的重要参数，能够最大化对动作空间的探索。合理的温度参数设置有助于实现对所有可行动作的迭代测试。因此，具有温度参数的更新如式（49）所示。

式中:πq为第q辆电动汽车的充电策略；H0为熵项。

式（47）至式（49）都是通过计算求最优化参数值。整个过程中，通过深度神经网络学习不断更新Q 值网络参数、策略网络参数以及温度参数，可使模型不断收敛，求解最优策略。

4.5 电动汽车充换电负荷优化调度整体流程

通过SAC 可以为大规模电动汽车用户制定考虑用户特征的电动汽车充电方案。同时，考虑换电站具有更强的可调度性能，采用SAC 算法、基于充电负荷的可调节情况对电动汽车换电站负荷进行进一步的优化调度，最终实现系统运行上的安全可靠性优化和市场运营上的经济性优化。整体的优化调度流程如图2 所示。

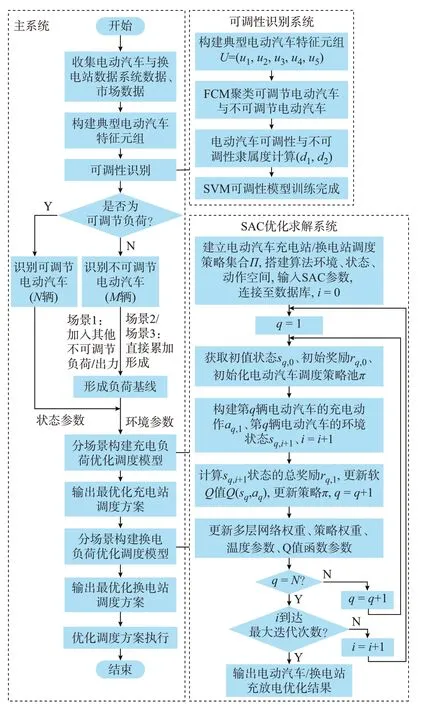
图2 基于SAC 的电动汽车充换电站负荷优化调度流程图Fig.2 Flow chart of optimal scheduling for SAC-based electric vehicle load for battery charging and swapping stations

5 算例分析

5.1 算例设计

以典型日场景下A 市充换电站聚合参与调度作为算例，收集A 市2 254 个充电桩的12 770 条充电数据，包括接入时间、结束时间、充电电量、充电结束原因等数据内容。其中，电动汽车的出行规律分布情况见附录C 图C1、图C2，原始充电电量分布情况见附录C 图C3，容量分布情况见附录C 图C4，电动汽车单日平均负荷规模约为12.5 MW，样本电动汽车规模为8 925 辆。以A 市典型换电站的换电负荷情况作为样本数据，换电站原始负荷分布情况见附录C 图C5，设置换电站共有充电机40 组，每组最大充电功率为75 kW，且具有备用电池80 组。在目前用户行为偏好标签数据库还不完善的情况下，设定无可调潜力的电动汽车的用户可调节隶属度为0，有可调潜力的电动汽车用户的可调节隶属度为1，车主均希望在离开之前将充电桩电量充满电。

场景1 的虚拟电厂负荷曲线见附录C 图C6。场景中的主要经济参数如表1 所示，其中，峰谷平时段划分的依据为基础负荷曲线的变化情况，分时段电价参照现行市场价格水平。辅助服务（调峰）开市时段为00:30—07:00 以及12:30—16:00，辅助服务市场价格为0.2 元/（kW·h）。

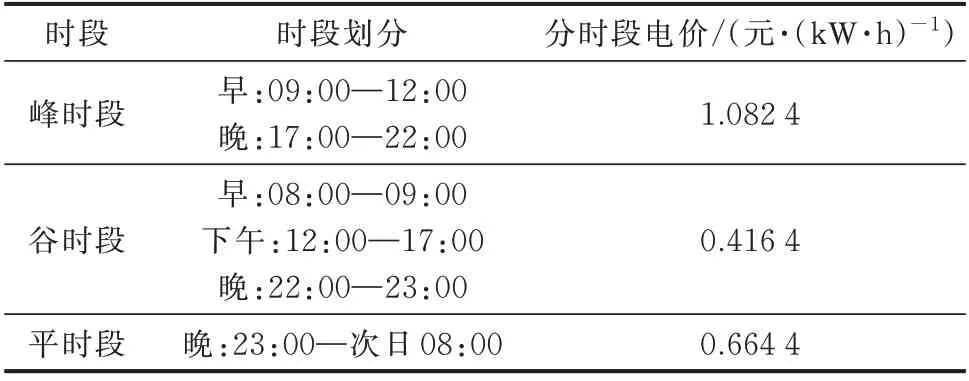
表1 电力市场参数Table 1 Electricity market parameters

计算过程中SVM 采用径向基（radial basis function，RBF）核函数，设置惩罚参数为1，核函数宽度参数为1/6。SAC 模型以32 条数据为一组训练批次，神经网络构建过程中设置3 层隐藏层，64 个神经元，学习率均为10-4。其他优化调度过程中的实施要点见附录C 表C1。

5.2 计算结果

5.2.1 可调节与不可调节识别结果

利用FCM-SVM 可对样本数据进行可调性识别，为验证模型效果，将FCM-SVM、k-means-SVM以及FCM-最邻近结点算法（KNN）模型的效果进行比较，对比结果如表2 所示。其中，准确率为模型分类准确的样本占总样本个数，精准率为模型分类结果为可调的样本中真实可调的样本比例，召回率为真实可调的样本中归类正确的样本所占的比例。

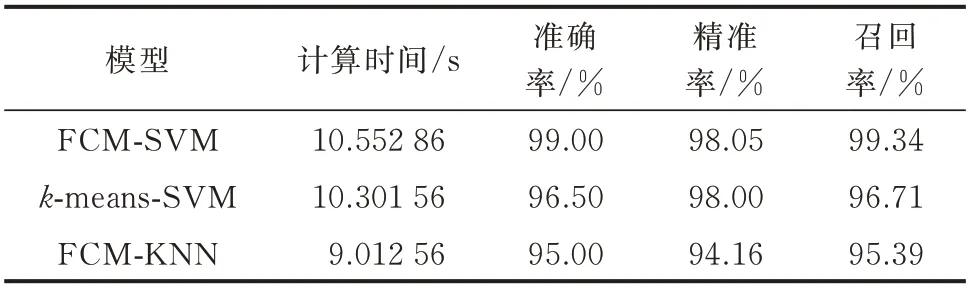
表2 模型识别效果对比Table 2 Comparison of model identification effect

由表2 可见，在本文场景中，FCM-SVM 在大数据识别计算时具有明显的分类精度提升，这将有利于电动汽车优化调度方案的落实，所牺牲的计算速度也在可接受范围内，是适用于本文场景的分类策略。

图3 为基于FCM-SVM 的电动汽车可调度情况识别结果，展示了96 个时段的可调节和不可调节电动汽车的负荷规模。

由图3 可见，可调节负荷规模与不可调节负荷规模相当，可调节负荷主要分布于时段0 至28、54至70、92 至96，即每日的13:30—17:30 和23:00—次日07:00。同时，从总体的负荷规模来看，样本所选充电桩站点的主要充电高峰有3 个，即05:00—07:00、12:30—18:00，20:00—次日01:00。

图3 电动汽车可调节与不可调节负荷规模Fig.3 Adjustable and nonadjustable load scale of electric vehicles

同时，随机抽样500 个典型样本，样本中不同可调性用户在充电时长、接入时长、充电功率、荷电状态和调节时长的分布差异分别如附录D 图D1 至图D5 所示。相对于不可调节负荷，可调节负荷具有充电时长和接入时长明显高、充电平均功率稍高、SOC 偏高、可调节时长更长的特征。具体来说，可调节电动汽车负荷充电时长偏向于1 h 上下，接入时长主要分布于2～5 h，充电功率大部分采用快充方式，SOC 状态主要分布于60%～80%，可调节时长主要位于1～6 h；不可调节电动汽车充电时长大部分位于1 h 以内，接入时长通常较短，荷电状态主要分布于70%～100%，可调节时长主要位于1～3 h。

5.2.2 电动汽车充电站调度结果

基于SAC 深度强化学习算法求解可调节电动汽车负荷的优化调度方案。经过16 h、训练1 500 次后，模型训练具有如附录E 图E1 所示收敛效果。为验证模型的实际调度效果，SAC 强化学习、AC（actor-critic）强化学习以及PG（policy-gradient）强化学习算法的计算效果对比如表3 所示，相关指标的说明见附录E 表E1。

由表3 可见，SAC 算法对于各类型的场景都具有更低的波动性和相对优秀的收敛性，尽管每回合运行时间相对较长，但是其测试回合的运行时间也不超过1 s。从附录E 图E1 还可以发现，SAC 具有更好的寻优效果，是适用于本文场景的优化求解算法。优化调度结果如图4 所示。

表3 不同模型优化调度效果对比Table 3 Comparison of optimal scheduling effects of different models

由图4 可见，3 种场景下的优化调度方案都实现了不同程度的峰谷差控制和负荷平抑效果，结合市场环境还创造了一定的收益。具体来说，场景1 的削峰填谷效果最为明显，降低了63%的负荷波动效果，EVA 收益增加了1 966.93 元/d，负荷峰谷差降低了510 kW，负荷率提升了7.84%。场景2 下的电动汽车优化调度方案降低了41%的负荷波动效果，EVA 收益增加了2 701.06 元/d，负荷峰谷差降低了315 kW，负荷率提升了5.23%。场景3 下的电动汽车优化调度方案受辅助服务市场的影响，具有最优的经济效益，降低了42%的负荷波动效果，EVA 收益增加了3 223.51 元/d，负荷峰谷差降低了321 kW，负荷率提升了3.31%。场景1 的负荷实时优化调度是迎合电力系统调度需求的结果，场景2与场景3 的负荷实时优化调度是迎合分时段电力市场价值变化的结果。整体协调调度的效果如表4所示。

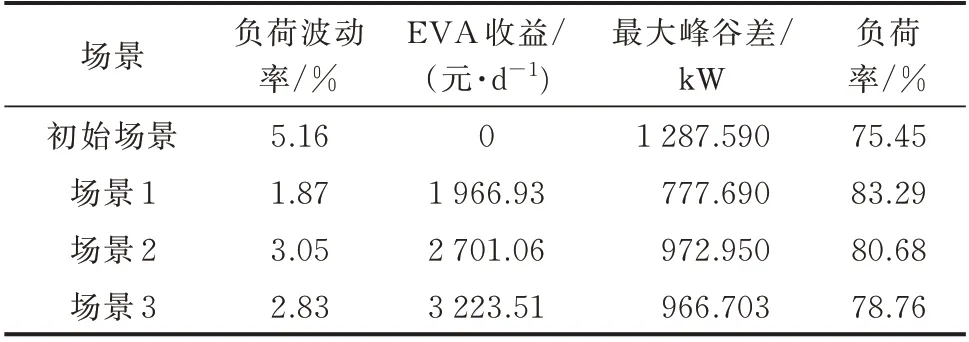
表4 整体协调调度效果Table 4 Effect of overall coordinated scheduling

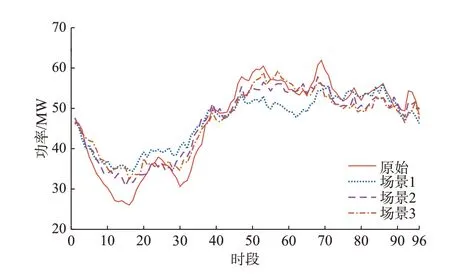
图4 基于SAC 的优化调度结果Fig.4 SAC-based optimal scheduling results

附录E 图E2 展示了不同场景下电动汽车优化调度后的可调节电动汽车负荷变化情况，附录E 图E3 展示了电动汽车总负荷变化情况。综合图E2、图E3 可见，场景1 中电动汽车负荷跟踪了虚拟电厂聚合负荷的变化情况，使得系统的总体负荷曲线波动性变小，但是电动汽车负荷曲线的波动性增强。场景2 和场景3 中电动汽车的负荷变化充分响应了市场分时段电价的激励，使得EVA 获得了最高市场效益，同时也使得电动汽车负荷曲线波动变大。

5.2.3 换电站进一步优化调度效果

在电动汽车优化调度完成之后，通过换电站的进一步优化调度可实现总负荷的进一步调整，优化调度完成后的系统总负荷情况如附录F 图F1 所示，换电站负荷经调节后的负荷变化情况如图5 所示。

图5 换电站优化调度结果Fig.5 Optimal scheduling results of battery swapping station

通过换电站的实时优化调度，进一步平滑了负荷曲线，场景1 中，通过换电站进一步优化了15%的负荷波动，降低了509 kW 的峰谷差与1.2%的负荷率；场景2 中，通过换电站进一步优化了1.1%的负荷波动，降低了315 kW 的峰谷差与1.1% 的负荷率；场景3 中，通过换电站进一步优化了0.9%的负荷波动，降低了320 kW 的峰谷差与0.7% 的负荷率。可见，换电站可对电动汽车负荷的优化调节结果做出进一步的优化。

6 结语

为解决EVA 促进电力系统经济可靠运行过程中的聚合资源实时优化调度问题，本文提出了基于SAC 深度强化学习的大规模电动汽车充换电负荷实时优化调度策略，以实现最优化聚合运行目标，结合仿真算例可以得出以下结论:

1）本文以EVA 为研究对象，从系统运行最优和经济效益最优的角度分别构建优化调度模型，可以实现平抑系统负荷波动、减少EVA 的充电成本并降低峰谷差的效果。

2）FCM-SVM 模型可实现电动汽车可调性识别，从中提取出可调节电动汽车负荷进行实时灵活调度；基于SAC 模型可为电动汽车充电过程和换电站电池的充放电过程制定个性化方案，实现充换电站的智能协调调度。

3）通过分析SAC 算法的收敛曲线并对比不同算法之间的结果稳定性、收敛速率、运行时间等内容，可以发现本文模型优化效果好、稳定性强，且运算速率较好，具有实际工程应用价值，适合解决大规模电动汽车接入的实时调度问题。

本文的研究成果可以应用于EVA 对大规模电动汽车资源的实时优化调度，但其互动机制仅限于EVA 与电动汽车资源之间，EVA 之间的竞争关系、EVA 内部的充电站和换电站之间的协调和平衡关系是后续研究的方向。

本文研究受到国网电动汽车服务有限公司的帮助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。