人口普查净覆盖误差估计

叶宝红，胡桂华

人口普查净覆盖误差估计

*叶宝红，胡桂华

（重庆工商大学数学与统计学院，重庆 400067）

针对我国和其它许多国家的政府统计部门在应用双系统估计量时，忽视对总体人口等概率分层、未考虑人口移动，以及未采取科学有效的方法计算双系统估计量抽样方差的问题，提出建立基于捕获-再捕获模型的双系统估计量及分层刀切抽样方差估计量的研究目标。为实现目标，采取现场调查、抽样估计及文献解读相结合的方法研究全面登记和抽样登记的双系统估计量及其方差估计。研究发现，双系统估计量须在等概率人口层建立及使用，否则产生异质性偏差，低估总体实际人口数及净覆盖误差。研究创新在于，在对美国人口移动处理方法深入研究的基础上，构造出适合于在我国应用的人口移动的、抽样登记的双系统估计量。研究价值在于，所建立的双系统估计量有望应用于我国2030年人口普查净覆盖误差估计。

事后计数调查；捕获-再捕获模型；分层刀切抽样方差估计量

0 引言

在每次人口普查中，有些人漏报，有些人多报。漏报人口数可能多于或小于多报人口数。如果漏报人口数多于多报人口数，就是净漏报；反之就是净多报。净多报或净漏报，统称为净普查覆盖误差。净漏报或净多报既可以表现为普查漏报与多报人口数之差，也可以表现为总体实际人口数与总体普查登记人口数之差。除加拿大等少数国家外，包括我国和美国在内的许多国家通过估计总体实际人口数，再将其减去普查登记人口数，得到人口普查净覆盖误差[1]。人口统计分析模型和双系统估计量是估计总体实际人口数的主流方法。人口行政记录健全的发达国家同时采用这两种方法估计净覆盖误差。发展中国家大多采用双系统估计量估计净覆盖误差。本研究采用双系统估计量估计净覆盖误差[2]。双系统估计量依据同一样本普查小区的事后计数调查人口名单和普查人口名单构造，其理论基础是最初估计野生动物总体规模的捕获-再捕获模型。事后计数调查在人口普查登记工作结束后实施，属于抽样调查，抽样单位通常是较小范围的地理区域，如我国的普查小区，平均含250人。

双系统估计量经历了四个研究阶段。经历了这四个研究阶段，才研发了用于人口总体规模估计的双系统估计量。

第一个阶段是其起源，即捕获-再捕获模型[3]。该模型等于对同一总体两次捕获的动物数目的乘积除以同时在两次捕获中同时捕获到的动物数目。丹麦的Petersen（1896）和美国的Lincoln（1930）是捕获-再捕获模型的创始人[4-5]。正是由于他们两人的研究，才产生了捕获-再捕获模型，称之为Lincoln-Petersen估计量。

第二阶段是将捕获-再捕获模型移植到人类总体构造全面登记的双系统估计量[6]。捕获-再捕获模型要求两次捕获均是对同一总体的全面捕获。然而，在事后计数调查中，我们无法得到总体的全面信息。这就需要首先假设事后计数调查是对总体的全面登记。另外，还需要对总体人口按照人口统计特征变量和地理位置变量交叉分层，形成若干等概率人口层[7]，在每个等概率人口层建立双系统估计量。如果直接在总体中构造双系统估计量，会产生异质性偏差，即由于总体人口在普查中登记概率不同而增大双系统估计量的分母，从而造成双系统估计量低估总体实际人口数。

第三阶段是构造人口移动的全面登记的双系统估计量[8-12]。在事后计数调查期间不可避免地会有人口移动。移动的人口共分为三种，即无移动人口（non-movers，缩写为）、向外移动人口（out-movers，缩写为）和向内移动人口（in-movers，缩写为）。向外移动人口是指人们从普查时居住的小区搬到了另外的普查小区。向内移动人口指的是人们事后计数调查时从原来的普查小区搬到了现在的普查小区居住。美国普查局提出了三种处理人口移动的方法，即A方法、B方法和C方法。其中C方法使用最为普遍。美国在2000年普查试点调查中测试了方法C，并且应用于2000年事后计数调查。方法C是指，使用向内移动者数目作为移动者数目，这是可靠的数据，因为它来自向内移动者本身。使用向外移动者匹配率估计移动者匹配率，以避免比对向内移动者出现的困难。

第四阶段是构造人口移动的抽样登记的双系统估计量[13-16]。在考虑人口移动情况下，双系统估计量公式中含有下列7个指标：人口普查登记人数、人口普查正确登记人数、无移动人数、向内移动人数、向外移动人数、无移动者中匹配人数、向外移动者中匹配人数，这里说的这7个指标都是总体值。在对人口有限总体实施概率抽样的条件下，须依据所用的抽样方法构造7个指标的估计量，用以代替公式中的7个指标，这样就是双系统估计量的估计量。

本研究创新体现在三个方面。一方面，从捕获-再捕获模型推导出双系统估计量，解析了它们之间内在的逻辑关系。另一方面，深入解读了美国普查局提出的处理人口移动的A方法、B方法和C方法。最后一方面，通过实际案例，全面演示了双系统估计量及其抽样方差估计量的详细计算过程，从而有助于双系统估计量在我国的推广应用。

1 捕获-再捕获模型

如果一次全面捕获无法得到满意的总体动物数目时，需要采取全面捕获-再捕获模型估计总体中的动物数目。全面捕获-再捕获模型的基本思想是，对总体进行第一次全面捕获，对捕获的动物做上记号，放回总体。等待几天，让做上记号的动物和在第一次全面捕获中没有捕获到的动物混合均匀。再次捕获同一总体的动物。如果这两次捕获相互独立，那么在第一次捕获中做上记号的动物数目比例就等于第二次捕获做上记号的动物比例。解这个方程，即可以得到总体动物数目的估计值。

表1 全面捕获-再捕获模型

Table 1 Full capture-recapture model

捕获情况在第二次捕获不在第二次捕获 在第一次捕获 不在第一次捕获

由表1得到：

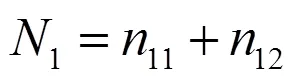
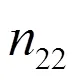
在上述的假设（尤其是独立性假设）下，如果一个个体在第一次全面捕获中捕获，则该个体在第二次全面捕获中捕获的概率为：

以及在第一次全面捕获中没有捕获而在第二次全面捕获中捕获的概率为：

式（2）和式（3）相同，故

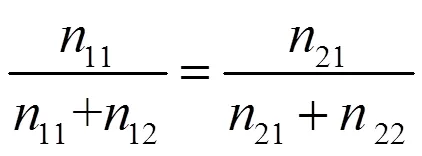
由式（4）可以得到：

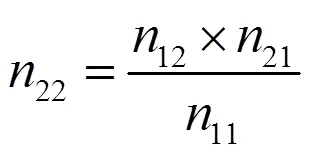
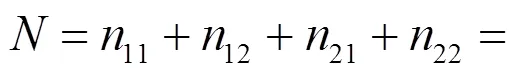
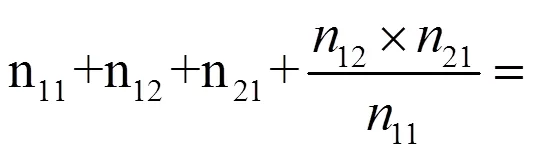
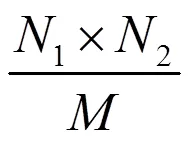
2 双系统估计量及其方差估计

2.1 双系统估计量

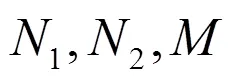
依据式（6）可得：

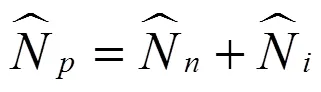
鉴于中国在历次人口普查质量评估中一直采取B处理方法，且找到向外移动者难度较大，以及向内移动者在本样本普查小区和了解向内移动者普查时点的登记地和登记情况不会遇到太大困难，于是采取B处理方法。此时事后计数调查人口由无移动人口和向内移动人口构成。相应地，事后计数调查匹配人口由无移动人口的匹配人口和向内移动人口的匹配人口构成。匹配人口指同时登记在普查名单与事后计数调查名单的人口。在事后计数调查比对实践中发现，有些人只登记在事后计数调查名单或普查名单。对事后计数调查的无移动人口，其普查名单和事后计数调查名单均在本样本普查小区，比对工作在同一样本小区内进行。向内移动人口，其普查名单在其他小区，事后计数调查在本样本小区。通过函证可以获悉向内移动者在普查中的登记情况。如果在本样本小区登记，在其他小区又进行了普查登记，那么向内移动者就是本样本小区的匹配人口。据此分析，式（8）变为式（9）：

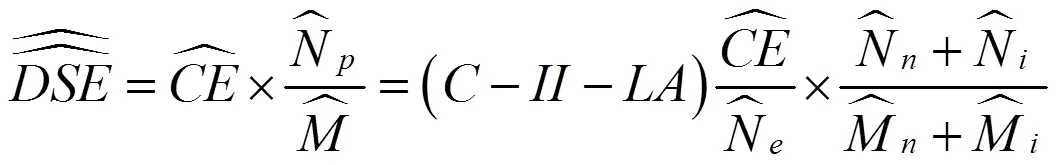
如果采取A构成法，那么式（8）变为式（10）：

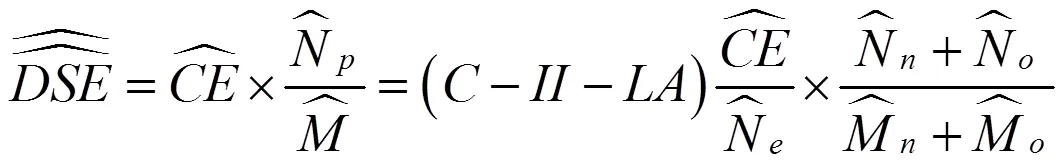
在事后计数调查日，向外移动者已经不在本样本普查小区，找到其本人难度不小，由其邻居提供其信息有误差。因此本文采取式（9）构造的双系统估计量。

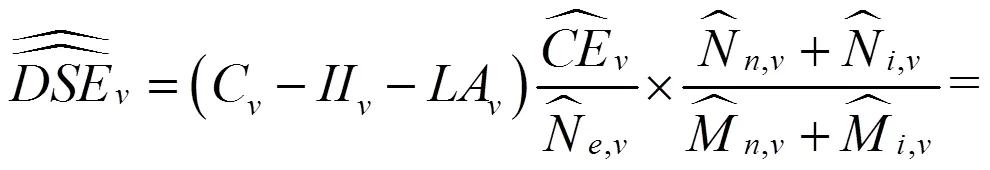
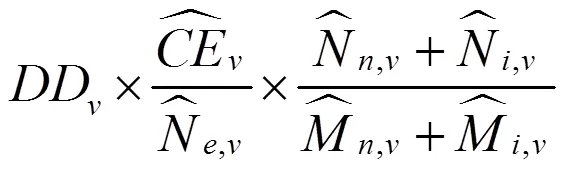
分层二重抽样适合于包括美国和中国在内的许多国家的人口普查质量评估的现实情况[17-20]。美国采用的抽样单位是街区群，中国采用的是普查小区。美国街区群规模差异大，在第一重抽样中需要按照街区群规模分层，在各个抽样层抽取第一重样本。在第二重抽样中，美国对第一重样本按照街区群地址误差率进一步分层，在各个新层抽取第二重样本。中国虽然普查小区规模差异小，但城乡普查小区存在较大差异，在抽取第一重样本前，需要对全国或省（自治区、直辖市）的普查小区按照城乡分层，在城市层和乡村层分别抽取第一重样本。对从城市层和乡村层抽取的第一重样本，按照调查难度再分层，在每个新层抽取第二重样本。

需要说明的是，本文采用的分层二重抽样与国内外出版的抽样调查专著有本质区别。区别在于，前者无论在第一重抽样，还是在第二重抽样之前，均对抽样对象进行了分层，并且两次分层采用的分层变量不同。

式（11）中的每一个估计量采取式（12）统一表示为：

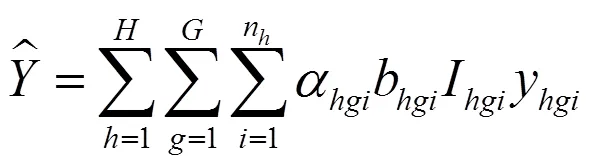
将式（12）代入式（11），即可以得到抽样登记的双系统估计量。

2.2 双系统估计量的抽样方差估计量

在构造双系统估计量后，还要构造其抽样方差估计量。从式（11）可以看出，双系统估计量是一个很复杂的估计量。对于复杂估计量，无法精确计算其抽样方差，只能近似估计。刀切法是近似计算复杂估计量方差的重要方法之一。刀切法是复制方法之一，复制方差估计在复杂抽样调查中十分受欢迎[21]。复制方法不需要计算泰勒展开式的偏导数，用户可以较为轻易得到方差估计值，而无需知道用于收集数据的抽样设计方案。提供复制权数后，用户分析数据结构不需要诸如层标识符之类的设计信息。

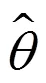
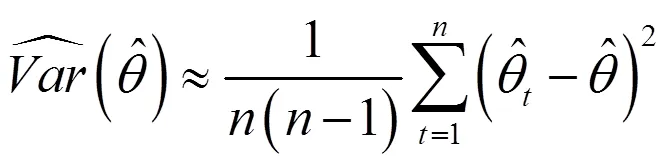
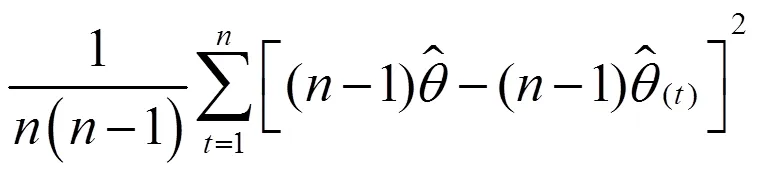
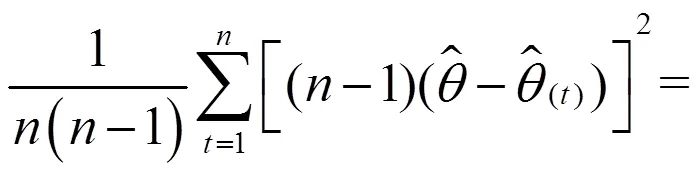
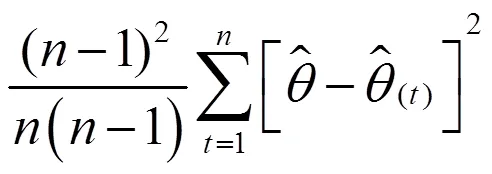
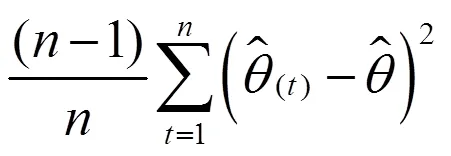
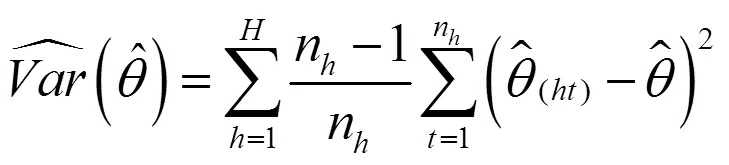
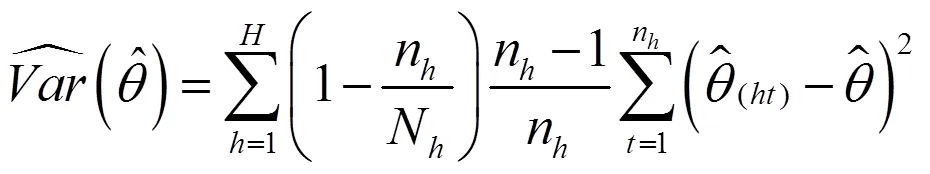
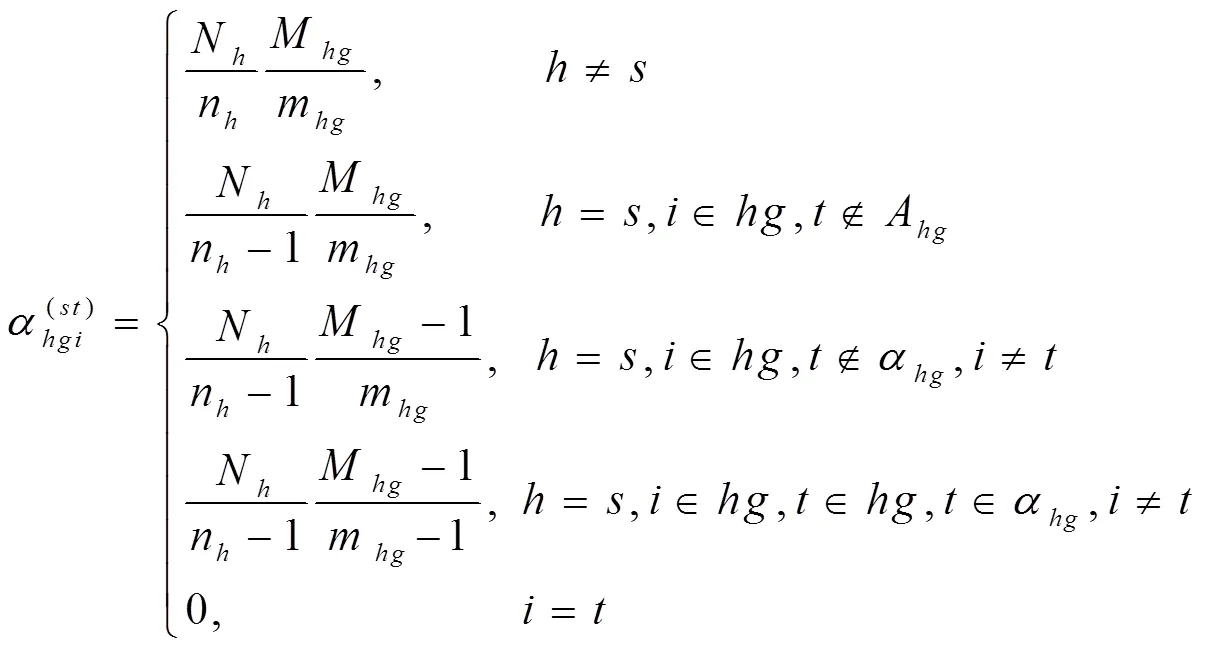
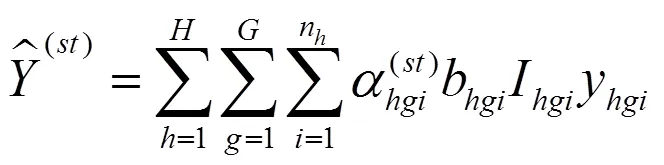
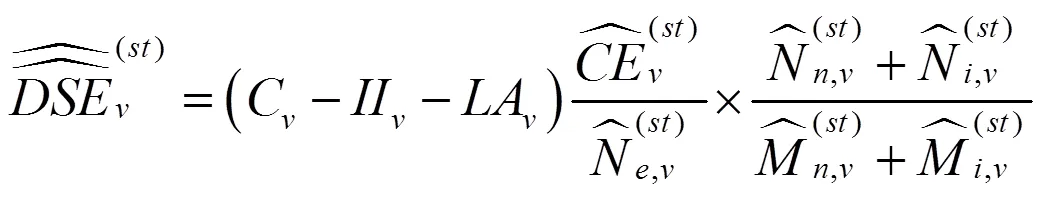
（21）

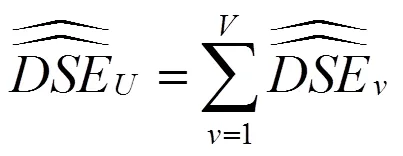
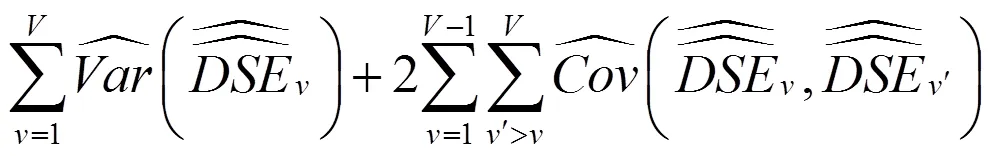
在式（23）中，

3 净覆盖误差估计

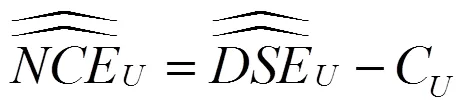
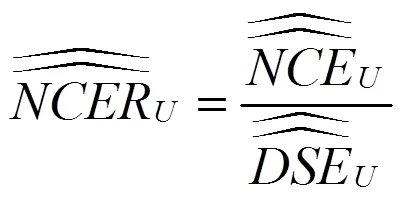
4 实证分析

4.1 资料来源及样本数据

实证对象是广西南宁市西乡塘区一个城乡交汇处，实证资料是第六次人口普查标准时点（2010年11月1日零时）上的普查人口名单及其事后计数调查人口名单。实证目标是估计这个城乡交汇处该时点的实际人口数及其净覆盖误差。获取资料的办法，是在与当地有关机构签订数据使用保密协议的情况，通过该机构调查取得数据。

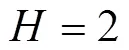
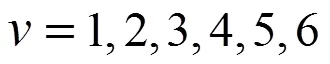
表2 - 表9中的数据是样本微观个人数据，是计算总体双系统估计值及其抽样方差估计值、协方差估计值、净覆盖误差估计值，以及小区域净覆盖误差估计值的基础。

表2 抽样层及样本量

Table 2 Sampling layer and sample size

层h层h小区总数层h样本小区总数层g层hg小区总数层hg样本小区总数

表3 样本普查小区抽样权数

Table 3 Sampling weights of the sample census

60071,1421,1,1√171 60071,1421,1,2√171 60071,1421,1,3171 60071,1421,1,4171 60071,2321,2,5√129 60071,2321,2,6√129 60071,2321,2,7129 40062,1322,1,8√100 40062,1322,1,9√100 40062,1322,1,10100 40062,2322,2,11√100 40062,2322,2,12√100 40062,2322,2,13100

注意：√表示第一重样本普查小区进入第二重样本，即1、2、5、6、8、9、11、12为第二重样本普查小区。

表4 等概率人口层“男、0-14岁”未加权样本人口数

Table 4 Unweighted sample population of “male, 0-14 years old” in equal probability population strata

样本小区普查登记人口数目标总体普查人口数无移动者人口数向内移动者人口数无移动匹配者人口数向内移动者匹配人口数 12922314243 22721293222 53023346253 62723315253 82819325213 93124333263 112822304233 123022356254

表5 等概率人口层“男、15-59岁”未加权样本人口数

Table 5 Unweighted sample population of "male, 15-59 years old" in equal probability population strata

样本小区普查登记人口数目标总体普查人口数无移动者人口数向内移动者人口数无移动匹配者人口数向内移动者匹配人口数 18369898747 27866858687 58771937745 67765815684 88170844723 98873936775 118067868716 1285699310738

表6 等概率人口层“男、60岁及以上”未加权样本人口数

Table 6 Unweighted sample population of "male, 60 years old and above" in equal probability population strata

样本小区普查登记人口数目标总体普查人口数无移动者人口数向内移动者人口数无移动匹配者人口数向内移动者匹配人口数 11513173142 21411152122 51713215154 61412164133 81512184133 91611205144 111510205124 121614194152

表7 等概率人口层“女、0-14岁”未加权样本人口数

Table 7 Unweighted sample population of “female, 0-14 years old” in equal probability population strata

样本小区普查登记人口数目标总体普查人口数无移动者人口数向内移动者人口数无移动匹配者人口数向内移动者匹配人口数 12421274233 22320253223 52623305243 62218266194 82419296215 92622326255 112320275213 122621305234

表8 等概率人口层“女、15-59岁”未加权样本人口数

Table 8 Unweighted sample population of “female, 15-59 years old” in equal probability population strata

样本小区普查登记人口数目标总体普查人口数无移动者人口数向内移动者人口数无移动匹配者人口数向内移动者匹配人口数 17768838706 27266799697 58170845724 67158755614 87563797666 98271899757 117461796656 127969869737

表9 概率人口层“女、60岁及以上”未加权样本人口数

Table 9 Unweighted sample population of "female, 60 years old and above" in equal probability population strata

样本小区普查登记人口数目标总体普查人口数无移动者人口数向内移动者人口数无移动匹配者人口数向内移动者匹配人口数 11715193162 21613182142 51816203152 61511173132 81613172141 91815214173 111614183152 121715182161

4.2 计算等概率人口层的实际人口数及净覆盖误差

首先依据式（12），以及表2 - 表9数据计算各个等概率人口层每个单元的加权人口数，见表10；然后获得各个等概率人口层的普查数据定义人口数，见表11；最后使用式（11）、式（22）、式（25）和表10数据，计算等概率人口层及总体的双系统估计值、净覆盖误差估计值，见表12。

表10 各个等概率人口层双系统估计量单元的加权人口数

Table 10 Weighted population of the dual system estimator units of each equal probability population strata

等概率层加权普查登记人口数加权目标总体普查人数加权无移动者人口数加权向内移动者人口数加权无移动匹配者人口数加权向内移动者匹配人口数 v=12862921987316454416238162929 v=28208768529878007084719005755 v=31515812029179453816134582887 v=42412920500279164816222423629 v=57608765826815137297688265855 v=61660013971185002729149421900

从表10可以看出，各等概率人口层的双系统估计量单元包括普查登记人数、目标总体普查人数、无移动人数、向内移动人数、无移动者匹配人数和向内移动者匹配人数。各单元人口数乘以相应层抽样权数可得各个等概率人口层双系统估计量单元的加权人口数。在表10中，以层=2为例，加权普查登记人口数为82087，加权目标总体普查人数为68529，加权无移动者人口数87800，加权向内移动者人口数7084，加权无移动匹配者人口数71900，加权向内移动者匹配人口数5755。

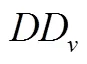
表11 各个等概率人口层的普查数据定义人口数（）

表11列示了各个等概率人口层的普查数据定义人口数。这些数据是已知数，是估计普查目标总体普查登记人口数的基础数据。须知，不能使用普查登记人口数作为估计普查目标总体普查登记人口数的基础数据。

表12 实际人口数、净覆盖误差估计值

Table 12 Actual population and estimated net coverage error

等概率人口层普查登记人口数实际人口数净覆盖误差 绝对数相对数（%） 男、0 - 14岁28973293854121.40 男、15 - 59岁800548164815941.95 男、60岁及以上1768917732430.24 女、0 - 14岁2699927026270.09 女、15 - 59岁79898801352370.29 女、60岁及以上1756417609450.26 总体25117725353523580.93

从表12可以看出：总体净覆盖误差为2358人，表明剔除普查多报人口数后在普查登记中净漏报2358人，净漏报率为0.93%。从各个等概率人口层的净覆盖误差率来看，“男、15 - 59岁”的净覆盖误差率最大，为1.95%，而净覆盖误差率最小的是“0 - 14岁”，为0.09%。这表明，前者在普查中的漏报严重，普查登记质量差；而后者的漏报情况最低，普查登记质量好。

4.3 计算等概率人口层及总体的抽样方差与协方差

双系统估计量复杂，抽样方差采取分层刀切抽样方差估计量近似计算。先使用式（16）和表3数据来计算复制权数，尤其是进入第二重样本的样本普查小区的复制权数，见表13。然后依据复制权数，使用式（18）、（19）、（21）和表4-表9数据计算等概率人口层的抽样方差和协方差，见表14。

表13 第二重样本普查小区的复制权数

Table 13 The replication weights of the second sample census

剔除小区1256891112 10300200200171171171171 23000200200171171171171 3150150200200171171171171 4150150200200171171171171 51501500200129129129129 61501502000129129129129 7150150100100129129129129 81001001001000160120120 91001001001001600120120 101001001001008080120120 111001001001001201200160 121001001001001201201600 131001001001001201208080

表14 等概率人口层及总体的抽样方差及协方差

Table 14 Sampling variance and covariance of equal probability population strata and population

等概率层男、0-14岁男、15-59岁男、60岁以上女、0-14岁女、15-59岁女、60岁以上总体 男、0-14岁247993 220090 86950 41093 -205035 -2133 388958 男、15-59岁220090 499853 -85491 -187728 89271 19455 555450 男、60岁上86950 -85491 355883 125904 -244963 -4299 233984 女、0-14岁41093-187728 125904 552817 -798298 106502 -159710 女、15-59岁-205035 89271 -244963 -798298 144156 -22092 -1036961 女、60岁上-2133 19455 -4299 106502-22092 240456 337889 总体388958555450233984-159710-1036961337889319610

表14为六个等概率人口层的抽样方差及协方差，该抽样方差及协方差矩阵是以各等概率人口层抽样方差为对称轴的对称矩阵。各个等概率人口层的抽样方差及该层与其他各等概率人口层的协方差之和即为总体的抽样方差及协方差。如表14中“女、0-14岁”层的抽样方差为552817 ，其与“男、0-14岁”、“男、15-59岁”、“男、60岁以上”、“女、15-59岁”、“女、60岁以上”层的协方差分别为41093、-187728、125904、-798298、106502。总体方差为319610。

5 结论

1）构造双系统估计量须满足的两个重要条件是：人口普查与事后计数调查相互独立；人口总体中的每一个人有同样的概率在普查中登记或者在事后计数调查中登记。在实际工作中，通过对人口普查质量评估工作进行一系列的制度规定来满足第一个条件。至于第二个条件，则是通过对总体进行登记概率同质性分层来满足。具体来说，就是寻找适当的人口统计特征变量和地理位置变量对总体人口分层。这些分层变量应当能够做到，把人口普查登记概率大致相同人口放在同一个层，把登记概率不同的人口放在不同的层。对这些选定的分层变量可以有两种使用方式。一种是用这些分层变量对总体分层（在实际操作中用抽样后分层来实现），分别在各层构造双系统估计量，然后将各层的估计量在整个总体（全国）进行合成；另一种是把选定的分层变量作为回归自变量，分别构造以人口的普查正确登记概率的Logistic变换为因变量，以及事后计数调查登记与普查登记匹配概率的Logistic变换为因变量的两个Logistic回归模型，对普查登记全国名单中每个人的普查正确登记概率预测值除以事后计数调查登记与普查登记匹配概率预测值的商求和，将其作为全国人口数目的估计量。可以证明，如果这里使用的回归自变量与前一种方式使用的分层变量相同，那么这里构造的估计量与前者的全国合成估计量相等。

2）人口普查质量评估中所使用的抽样方法属于复杂抽样设计，所以双系统估计量的估计量方差不能用数学解析式直接计算，而需要选择适当的近似方法来估计。使用“大折刀”方法。它是把第一步样本中的各个抽样单元（普查小区）逐一重置轮换切掉，每刀切一个单元之后，用样本中余下的其他抽样单元，按双系统估计量的估计量计算程序，计算切掉该单元的切断后复制估计量。每个样本单元的切断后复制估计量，与无切断估计量的差平方的平均值即为所需要的“大折刀”估计方差。在这里，各个切断后复制估计量与无切断估计量相比，除了丢失掉一个样本单元之外，余下的各个抽样单元的抽样权数，也会随着它们各自与被切掉单元之间关系的不同情况，而发生不同的改变。

[1] 冯乃林,李希如,武洁,等.人口普查的事后质量抽查 [R]. 国家统计局人口和就业统计司, 2012.

[2] 胡桂华.人口普查净误差估计综述 [J]. 数理统计与管理, 2018, 37 (5): 796-814.

[3] 杨贵军,徐文哲,林意智. 关于捕获-再捕获抽样的置信区间 [J]. 统计与信息论坛, 2013, 28 (7): 9-14.

[4] Petersen C G. The yearly immigration of young plaice into the limfjord from the german sea [R].Danish Biological Station, 1896.

[5] Lincoln F. Calculating Waterfowl Abundance on the Basis of Banding Returns [J].Circular of the Department of Agriculture,1930,118 (6): 1-4.

[6] Sekar C C, Deming W E. On a method of estimating birth and death rates and extent of registration [J]. Journal of the American Statistical Association, 1949, 44 (5): 101-115.

[7] 胡桂华.人口普查质量评估中抽样后分层变量的选择 [J]. 数理统计与管理，2015, 34 (2): 254-263.

[8] 迟璐婕,胡桂华. 人口数目估计的多来源方法 [J]. 徐州工程学院学报, 2021, 36 (2): 84-92.

[9] 胡桂华,莫锦萍,涂火年. 基于捕获-再捕获模型的双系统估计量模型式框架[J]. 徐州工程学院学报：自然科学版, 2012, 27(4):23-29.

[10] 胡桂华,孙晓宇,康颖,等.人口抽样调查方案设计研究[J].徐州工程学院学报, 2017, 32(4): 24-29.

[11] 胡桂华,武洁. 人口普查质量评估理论与实践[M].北京: 中国社会科学出版社, 2016.

[12] 胡桂华,丁宣浩,陈义安,等.人口普查覆盖误差估计量研究 [J]. 数理统计与管理, 2018, 37(1):1-12.

[13] Statistics South Africa. Census 2011 Post-enumeration Survey: Results and Methodology [R]. Statistics South Africa, 2012.

[14] U.S. Census Bureau. 2020 Census detailed operational plan for: Post-enumeration survey operation [M]. Washington: U.S. Census Bureau, 2020.

[15] U.S. Bureau of the Census. Accuracy and coverage evaluation of census 2000: Design and methodology [R]. U.S. Census Bureau, 2004.

[16] Patrick J. Cantwell. Dual-system estimation [M]. Springer:Springer Nature, 2015.

[17] 金勇进.抽样:理论与应用[M]. 2版.北京:高等教育出版社, 2016.

[18] 胡桂华.人口普查净误差构成部分的估计[J].统计研究,2011, 28( 3): 90-100.

[19] 胡桂华,武洁. 人口普查质量评估中Logistic回归模型的应用 [J]. 数量经济技术经济研究，2015(4):106-122.

[20] 胡桂华,吴东晟. 人口普查质量评估调查的抽样设计[J]. 数量经济技术经济研究，2014(4):113-129.

[21] 胡桂华,杜艾卿. 基于单系统估计量的人口普查内容误差估计 [J]. 数理统计与管理, 2018, 37(6): 951-963.

ESTIMATION FOR NET CENSUS COVERAGE ERROR

*YE Bao-hong, HU Gui-hua

（School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China）

In view of the problems that the government statistical departments of our country and many other countries ignore the equal probability stratification of the overall population, do not consider population movement, and fail to adopt scientific and effective methods to calculate the sampling variance of dual-system estimator, when applying dual-system estimator, the research objective on constructing the dual-system estimator and the stratified Jack-Knife sampling variance estimator based on the capture-recapture model is proposed. In order to achieve the goal, a combination of field survey, sampling estimation and literature interpretation is adopted to study the dual-system estimator with complete enumerations and sampling enumerations and its variance estimation. The study finds that the dual-system estimator must be established and used in the equal-probability population stratum, otherwise a heterogeneous bias will occur, which will underestimate the overall actual population and net coverage error. The research innovation lies in the establishment of a dual-system estimator with population movement and sample enumerations, which is suitable for the application in our country based on the in-depth study of the US population movement processing methods. The value of the research is that the established dual-system estimator is expected to be applied to the net coverage error estimation of the 2030 census in our country.

post-count survey; capture-recapture model; stratified Jack-knife sampling variance estimator

1674-8085（2022）01-0008-12

O212

A

10.3969/j.issn.1674-8085.2022.01.002

2021-07-17；

2021-09-25

全国统计科学研究重点项目(2019LZ28)；教育部人文社会科学研究规划基金项目(20YJ910002)

*叶宝红(1996-)，女，重庆璧山人，硕士生，主要从事人口普查质量评估研究(E-mail:820462824@qq.com).