无缝型桥梁拱型搭板的可行性研究
庄一舟,陈益楠,郑国平
(浙江工业大学 土木工程学院 杭州市 310014)
0 引言
桥梁搭板首先要减少由于回填土沉降引起的路面垂直变形,其次是在桥梁和路堤之间提供平滑过渡,作为无缝桥搭板还需要考虑主梁温度变形传递的纵桥向位移问题[1]。搭板脱空沉降等所带来的颠簸问题不是一个重大的安全问题,而是一个昂贵的维护问题。研究动机是寻找一种可行的新型搭板构造形式,来解决目前所存在的无缝桥搭板问题。
从拱的传力原理获得灵感,“拱”主要依靠顺拱轴线的轴压力流来传递竖向荷载。其传力方式采用了“导”的方式,力线简洁,传力路径较短,且构件应力分布均匀,能充分发挥材料强度,根据其特性提出无缝桥拱型搭板构造(如图1)。作为搭板,主要是以受压为主,拱型能够完美传力,可以有效缓解结构因应力集中等问题引起的变形甚至断裂,还可以通过拱型跨长的设置提高搭板结构适应变形的能力,减少端部的水平位移,防止造成路面过度沉降,发生开裂现象。拱型搭板构造下部可填软土或选择脱空,这有效避免了桥台牛腿受到台后土体上翘直接挤压路面上部连续结构,引起路面上部连续产生拉应力而造成上表面混凝土的受拉开裂,这一构造措施达到释放牛腿端部的竖向和转角位移所产生的应力效果。

图1 拱型搭板示意图
以矢跨比为1/5的拱型搭板为例,利用有限元计算分析开展其在无缝桥主梁温度变形传递纵桥向位移(μ)情况下的受力分析,探究拱型搭板在无缝桥应用中的可行性。
1 有限元计算模型
利用ABAQUS有限元软件,建立三维具有拱型搭板的无缝桥梁路桥过渡段模型,无缝桥梁路桥过渡段结构为“路面铺装层+拱型搭板+地基土体”。所建立的三维有限元模型所选取的模型参数包括:模型尺寸、模型材料本构、接触设置及荷载边界条件设定,相关参数值参考了文献[2]的研究结果,具体论述如下。
1.1 结构模型参数
(1)模型尺寸
基于实际无缝桥梁路桥过渡段结构体系,并综合考虑计算精度和计算效率,及拱型搭板与土层为典型的平面应变模型[3],故对模型取1m宽建立搭板-土有限元计算实体模型,建立的带有拱型搭板的无缝桥梁路桥过渡段有限元模型基本尺寸见表1。

表1 具有拱型搭板的无缝桥梁路桥过渡段有限元模型基本尺寸
其中拱型搭板,计算矢高为1.6m,跨径为8m,矢跨比为1/5。
(2)本构关系
为反应不同材料之间的应力-应变关系,ABAQUS在进行有限元计算时,需为不同材料赋予相应的本构模型。计算模型中各结构层对应材料沥青混凝土、C30混凝土和泡沫混凝土均采用线弹性模型,路堤填土和强风化熔岩则采用摩尔库伦本构模型进行模拟,各种材料的具体参数见表2所示。

表2 模型结构层材料参数取值[4]
1.2 接触及荷载设置
在拱型搭板与土层模型有限元计算分析中,需要考虑到拱型搭板与土以及各类土与土之间的接触[5]。模型中接触对均采用面面接触,并依据原则定义主从面:在接触中选择刚度大的面作为主面,如果两个接触面的刚度相似,则应选择网格较为粗的面作为主面。接触属性设置为罚摩擦接触,搭板与土层之间切向行为的摩擦系数为0.69,各土层之间为0.2;法向行为均采用“硬”接触。除路面铺装层外,其余四面及底面均设置人工边界。根据工程实例搭板监测数据以及理论方面的计算,对近台端拱脚参考点施加单向μ=±20mm的位移以模拟主梁受温度影响在纵桥向的胀缩变形,远台端拱脚设置固接于枕梁。
1.3 模型网格划分
根据上述模型尺寸取值,建立带有拱型搭板的无缝桥梁路桥过渡段模型,如图2所示。
有限元模型中,经误差分析,按图2所示的网格进行划分,其中拱型搭板及搭板上方填土,进行网格加密处理。本模型网格单元类型选用八结点线性六面体缩减积分单元(C3D8R)。

图2 有限元计算模型网格三维图
1.4 模型计算步骤
(1)初始地应力平衡,对整个模型施加重力及包括搭板桥台面的5面人工边界,并采用ABAQUS自动地应力平衡模式来平衡台后填土地应力[6],确保模型初始状态具有初始应力而无竖向位移,平衡之后模型最大竖向位移为1.369×10-4m,如图3(U2为模型竖向位移),满足精度要求。

图3 初始地应力图
(2)激活搭板与土体及土层之间的面面接触对及俩拱脚的固定连接状态。
(3)释放搭板桥台面边界限制及近台端拱脚约束,并对其施加单向μ=±20mm的位移,以模拟主梁受温度影响在纵桥向的胀缩变形。
2 模型计算结果
基于上述建立的带有拱型搭板的无缝桥梁路桥过渡段有限元模型,模拟得到拱型搭板受到单向推拉状态下,计算模型中搭板、板上土层及路面的竖向变形云图,如图4和图5所示。
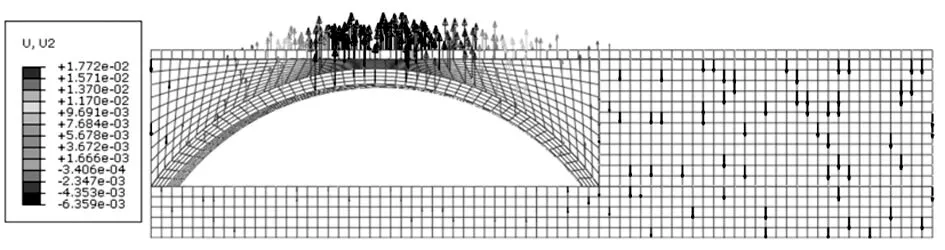
图4 搭板单向受推(μ=20mm)时竖向变形云图

图5 搭板单向受拉(μ=-20mm)时竖向变形云图
对比图4和图5,在拱型搭板受到单向推拉时,搭板最大竖向变形均发生在拱顶处,可以发现受推相对受拉情况下对搭板及上方填土竖向变形影响较大,其拱顶处变形达到1.772×10-2m。分别作出拱型搭板在两种受力情况下所对应的路面竖向沉降曲线图(图6、图7),展示了在拱型搭板单向受推和受拉情况下,在搭板处路面沉降呈现出“拱”状和倒“拱”状的曲线形态,说明拱型搭板充分利用自身构造形状及材料特性,较好地缓解纵向位移并传递至土体进行吸收,可以有效解决断板问题以及减少端部的水平位移。

图6 受推作用下路面沉降

图7 受拉作用下路面沉降
路面平整度是分析搭板-土之间相互作用的关键控制指标。瑞士规范[7]采用坡度变化准则χ来量化路面的平整度,详见式(1)。其中坡度系数χ考虑了沉降的深度和长度,为局部曲率半径提供了有效的评估方法。由式(1)定义的坡度系数χ必须始终低于极限状态χadm值为28‰,高速公路的χadm值为20‰。
(1)
依据瑞士规范对路面平整度的定义,计算出拱型搭板在单向受推、受拉情况下相应的坡度系数χ,并相对应作出两种情况下的路面平整度坡度系数曲线图如图8所示。

图8 搭板在受推和受拉作用下的路面平整度
从图8可以得知,拱型搭板在受推和受拉情况下产生的最大坡度系数均发生在拱型搭板末端所对应的水平路基距离处附近,分别为±7‰,远远低于高速公路极限状态20‰,所以带有拱型搭板的无缝桥路基表面的平整性能够满足瑞士规范的容许限值要求。综合来看,拱型搭板可以提高整体搭板结构适应变形的能力,能够有效地缓解路面上表面产生的应力,防止路面出现裂缝,产生颠簸。
3 结论
合适的搭板设计直接影响交通基础设施的安全性和经济性,提出一种拱型搭板构造形式,通过模拟拱型搭板在主梁纵桥向变形下的竖向沉降情况及对路面平整度进行分析研究,发现拱型搭板可以较好地利用本身构造来吸收无缝桥的纵桥向位移及提供桥梁到路堤的平滑过渡,得出拱型搭板可以作为无缝桥缓解主梁温度变化带来的纵桥向位移及路桥过渡段所造成的颠簸现象的解决途径之一,能在一定程度上减缓结构变形和常规搭板末端带来的应力集中等问题,可以在无缝桥领域得到一定的应用。对于拱型搭板而言,其构件本身参数及两端拱脚的连接方式仍需要进一步进行推导计算、数值模拟以及相关试验来优化。目前有关拱型搭板受力性能的分析尚存在许多不足,希望通过讨论,使拱型搭板技术能够在今后的设计实践中得到进一步的推广与完善。

