基于MATLAB下的制动系统建模、仿真及ABS控制器设计

王凯凯 董琴琴 陈作

摘要： 本文对某汽车ABS制动系统进行仿真建模，并对其进行单轮模型和分段线性的轮胎模型的建立;在Matlab环境下对ABS控制器进行设计和仿真分析;提出了一种门限值控制算法，对制动液压控制系统实现增压、保压、减压动作，使得汽车制动时的滑移率控制在一定范围内，以保证汽车的平稳制动。得出ABS控制下的滑移率时域结果图、车轮前进速度与车轮线速度关系曲线、制动器制动力矩与地面制动力随时间变化曲线。仿真结果表明：在门限值控制算法下设计的ABS控制器能够将滑移率有效地控制在理想范围内，车轮前进速度近似一条直线，加速度趋于定值，且防止了车轮过早抱死，说明在此基础上设计的控制器能够使得汽车平稳制动。

Abstract： In this paper， the simulation model of an automobile ABS braking system is established， and the single wheel model and piecewise linear tire model are established; The ABS controller is designed and simulated in Matlab environment; A threshold control algorithm is proposed to realize the pressurization， pressure holding and pressure reduction of the braking hydraulic control system， so as to control the slip rate in a certain range， so as to ensure the smooth braking of the vehicle. The time domain results of slip rate under ABS control， the relationship curve between wheel forward speed and wheel linear speed， and the variation curve of brake torque and ground braking force with time are obtained. The simulation results show that the ABS controller designed under the threshold control algorithm can effectively control the slip rate within the ideal range， the forward speed of the wheel is close to a straight line， the acceleration tends to a fixed value， and prevent the wheel from locking prematurely. It shows that the controller designed on this basis can make the vehicle brake smoothly.

關键词： 制动系统;ABS控制器;建模仿真

Key words： braking system;ABS controller;modeling and simulation

中图分类号：TP273                                      文献标识码：A                                  文章编号：1674-957X（2022）05-0011-03

0  引言

随着载重车辆动力性的不断提高，客观上也对车辆的制动性能与驱动性能提出了越来越高的要求。随着载重车辆的不断细化与发展，载重车辆的驱动性能日渐优异，与此同时对载重车辆的制动性能也提出了更高的要求。由于车辆运动状态的复杂性和车轮与地面之间的附着力的非线性等因素，车辆在高速行驶中制动或在弯道上紧急制动以及在冰雪路面等复杂路况下运动时，经常会出现车轮因抱死拖滑而导致制动距离过长，同时还有车身侧滑掉头，失去方向控制能力，车轮滑转等现象。然而，由于车辆本身运动状态及路面状态都是复杂未知的，静止状态下性能良好的车辆在某些极限状态下紧急制动时，会出现多种不安全的情况，比如：车辆在高速行驶中制动、在弯道上紧急制动、在冰雪路面等复杂路况下运动时等等，车辆都有可能出现车轮因抱死拖滑而导致制动距离过长，失去方向控制能力，车轮滑转等现象。甚至还有可能出现车身侧滑、掉头、翻转等更严重后果。车辆防抱死制动系统（ABS）是一种在紧急制动情况下自动控制制动器制动力的大小，使车轮不被抱死，处于边滚边滑的状态，以保证车轮与地面的附着力在最大值。使汽车制动距离尽可能缩短，同时保持汽车方向稳定性和转向操纵能力的装置。

李少廷等[3]通过Matlab/simulink建立汽车防抱死制动系统模型，控制器控制滑移率大小，通过仿真验证了ABS制动系统拥有良好的制动性和操纵性。王勐等[4]提出了一种基于动能转化建立制动系统的新方法，通过对有防抱死系统和无抱死系统两种情况进行比较，结果表明基于动能转化分析的过程是可行的。付强等[5]提出了一种汽车主动空气阻力制动系统（APB）方法，利用Simulink建立模型进行仿真研究，试验结果表明APB控制能够达到缩减制动距离和制动时间的目的。本文利用Matlab编写相关程序，带入相关参数，用以模拟汽车防抱死制动系统和ABS控制器，采用门限值算法对滑移率进行控制，得出相关图形及数据。上述文献均未使用此方法进行建模仿真。

1  ABS的组成及工作原理

车辆防抱死制动系统（ABS）能够在紧急制动情况下使汽车的制动距离尽可能地缩短，并保持汽车的方向稳定性和转向操纵的能力。车辆防抱死制动系统（ABS）在紧急制动情况下自动控制制动器制动力的大小，车轮会处于边滚边滑的状态，以保证车轮与地面的附着力保持在最大值。尽可能缩短汽车制动距离，同时保持汽车方向稳定性和转向操纵能力的装置，保持行车安全。

ABS 通常由车轮转速传感器、制动压力调节装置、电子控制装置ECU和ABS警示灯组成[1]。汽车在制动过程中，首先车轮转速传感器将会采取到各个车轮的转速，然后将信号输入给ECU，再由ECU对采集到的信号进行分析，从而得到各个车轮的运动状态，并发出相应的控制指令，发送给制动压力调节器，由制动压力调节系统对制动管路油压高速地进行“增压-保压-减压”的循环调节过程，将各车轮滑移率范围控制在最佳范围内，从而缩短制动距离，提高车轮制动时的方向稳定性。ABS的工作原理如图1所示。

2  动力学建模

2.1 单轮模型  忽略空气阻力与车轮滚动阻力，系统的运动方程如下所示。

其中：m——单轮模型质量;rd——车轮滚动半径;Iw——车轮转动惯量;ω——车轮旋转角速度;uw——车轮轮心前进速度;Fxb——地面制动力;Tb——作用于车轮的制动力矩;μ——路面附着系数;Fz——地面作用于车轮的法向反力，Fz=mg。

单轮制动力学模型[2]如图2所示。

2.2 “魔术公式”轮胎模型  “魔术公式”轮胎模型由Pacejka教授提出，它以三角函数组合的形式来拟合轮胎试验数据，由Pacejka教授提出的“魔术公式”轮胎模型使用了三角函数组合的形式来拟合轮胎实验数据。得出了一套形式相同并可同时表达纵向力、侧向力和回正力矩的轮胎模型。其形式如下：

式中，y可以是纵向力、侧向力和回正力矩，在不同情况下x可表示轮胎侧偏角或纵向滑移率。

通过Matlab编程，得到“魔术公式”下的轮胎附着系数与滑移率之间的关系图像（图3）。

2.3 分段线性的轮胎模型  路面附着系数与车轮滑移率之间存在一定的非线性关系。“Dugoff”模型用两段直线来近似表示路面附着—滑移曲线（μ-sb曲线），可得到分段线性化的附着系数μ和车辆滑移率sb的关系。表达式如下所示。

其中μh——峰值附着系数，μh=0.8;μg——车轮完全抱死（即sb=1）时的路面附着系数，μg=0.6;s0——峰值附着系数所对应的滑移率。车轮滑移率表示车轮被驱动时（制动时）相对于纯滚动状态的偏离程度。

车轮的滑移率在0～1之间变化。当车轮做纯滚动时，即uw=rdω，此时sb=0，当被驱动轮处于纯滑动状态时，sb=1。线性化的路面附着系数与车轮滑移率关系曲线如图4所示。

3  仿真流程及控制算法

3.1 ABS仿真流程  利用路面附着系数与滑移率的关系曲线所表示的轮胎模型，控制滑移率上限smax及下限Smin，制动器油压增长率ki和减小率kd，以及车辆模型参数和初始参数等数据信息进行ABS控制器的设计。

据分析可知，控制逻辑实现的关键是计算当前车轮滑移率sb（t）并与预先确定的门限值进行比较，来判断是否对制动液压控制系统进行增压或减压操作。由分析可知，ABS系统会将当前车轮滑移率sb（t）与预先确定的门限值进行比较，再由逻辑系统控制是否对制动液压系统进行增压、减压或者平衡的操作。

3.2 门限值控制算法  为保证车轮滑移率在最理想的范围内，采用门限值控制算法。本文使用门限值算法，以确保滑移率在最理想的区间内。制动开始后，随着制动压力的升高，车轮转速ω相应减小，车轮随即出现滑移;当车轮滑移率达到理想范围的上限值smax时，减少制动压力，随着制动压力的减少，滑移率随即逐渐减少，直至减少到滑移率下限smin时再增大制动压力。当制动开始后，液压油压力不断升高，卡钳在制动盘上压力增大，使车轮转速ω降低，车轮开始出现滑移;当车轮滑移率达到理想区间内的上限值时，系统控制液压油压力降低，卡钳在制动盘上压力减小，车轮转速ω增大，车轮滑移率开始降低，直到达到滑移率的下限后再增大制动压力。

循环往复上述过程，直至车辆停止运动。ABS系统将贯穿整个刹车过程，循环往复控制制动压力变化直到车辆停止运动。在ABS控制器起作用的过程中，门限值控制算法能将滑移控制在理想范围内，即smin？燮sb？燮smax，由此可保证车辆的最佳制动性能及行驶方向控制的稳定性。

4  实验与结果分析

4.1 实验参数

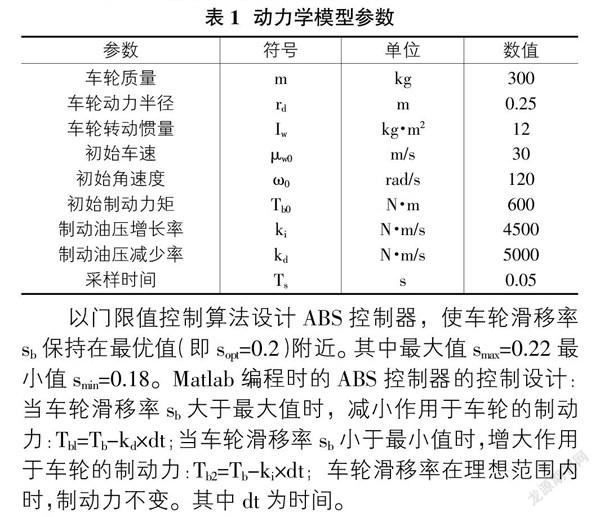
单轮ABS制动力学模型参数如表1所示。

以门限值控制算法设计ABS控制器，使车轮滑移率sb保持在最优值（即sopt=0.2）附近。其中最大值smax=0.22最小值smin=0.18。Matlab编程时的ABS控制器的控制设计：当车轮滑移率sb大于最大值时，减小作用于车轮的制动力：Tbl=Tb-kd×dt;当车轮滑移率sb小于最小值时，增大作用于车轮的制动力：Tb2=Tb-ki×dt;车轮滑移率在理想范围内时，制动力不变。其中dt为时间。

4.2 结果分析

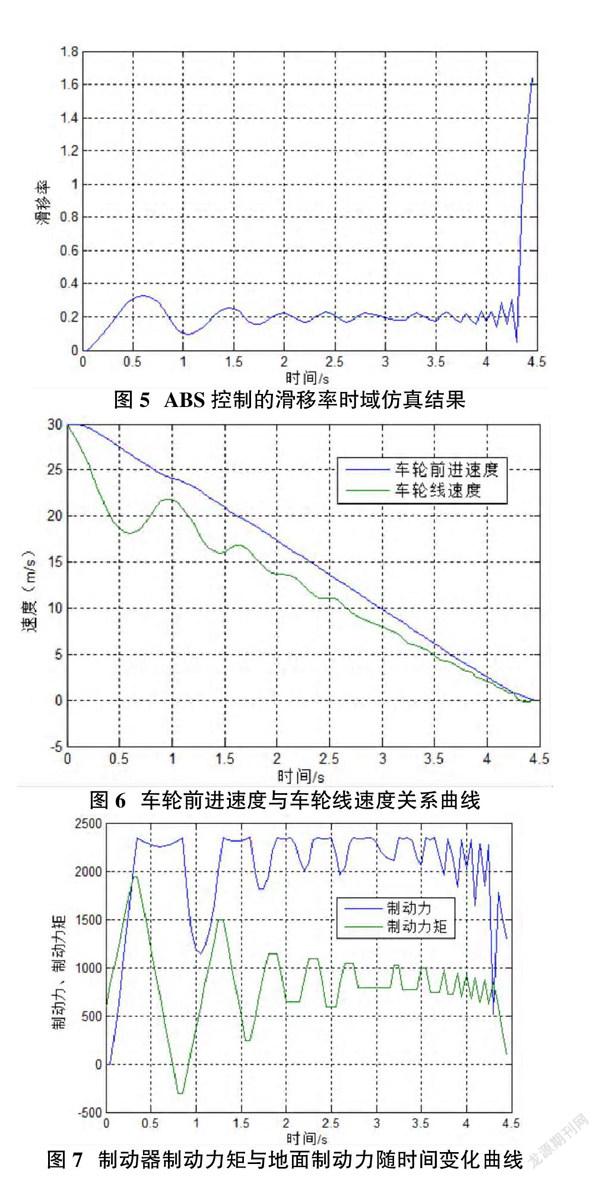
根据单轮制动动力学模型参数及路面附着系数，通过MATLAB编程，得到ABS控制的滑移率时域结果图、车轮前进速度与车轮线速度关系曲线、制动器制动力矩与地面制动力随时间变化曲线（图5-图7）。

仿真结果表明：从基于门限值控制算法下的滑移率—时间曲线图像中可以看出，制动过程中，滑移率逐渐控制在0.18～0.22之间，待汽车完全停止运动时，车速为零，根据制动时滑移率公式可知，此时滑移率趋于无穷大，所以在仿真最后一段，滑移率有较大波动。所以在仿真接近结束时，滑移率的波动达到最大值。车轮前进速度几乎呈线性减小，加速度趋于定值，说明汽车制动过程中稳定性较高。车轮线速度在汽车制动前期有小许波动，逐渐趋于平稳并趋于零，此时滑移率趋于无穷，与图5图形吻合。

制动器制动力矩在滑移率控制器的控制下，完成了增压、保压、减压动作，防止车轮过早抱死，减小制动距离。制动器在滑移率控制器的控制下，通过液压系统调整“增压、保压、减压”的状态从而调整制动力矩，防止车轮过早抱死，从而延长制动距离，确保行车安全。

5  结论

①以单轮为例，建立单轮动力学模型。通过线性化的路面附着系数与车轮滑移率，建立分段线性的轮胎模型。②运用门限值控制算法，将滑移率sb控制在0.18～0.22之间，实现了制动器的减压、保压和增压动作，减少了制动距离并有效地防止了车轮的过早抱死，提高了制动时的稳定性。③通过仿真流程运用MATLAB软件进行编程，得到了滑移率时域结果图、车轮前进速度与车轮线速度关系曲线、制动器制动力矩与地面制动力随时间变化曲线。仿真结果表明：所设计的ABS控制器能够有效地使汽车平稳制动。

参考文献：

[1]劉家员，等.ABS对制动系统性能提高分析及研究[J].时代农机，2016，43（03）：40-42.

[2]胡启国，等.车辆ABS参数自调节模糊PID控制仿真[J].重庆交通大学学报，2012，31（02）：344-352.

[3]李少廷，等.基于simulink的汽车防抱死制动系统的仿真研究[J].山东理工大学学报，2016，30（05）：44-48.

[4]王勐，等.基于动能转化的汽车制动模型的建立及仿真[J].黑龙江工程学院学报，2008，22（01）：60-63.

[5]付强，等.汽车主动空气阻力制动系统仿真研究[J].机械设计与制造，2012，03：60-62.

作者简介：王凯凯（1994-），男，河南商丘人，本科学士，工作于南充科技职业学院工程与应用技术学院，主要从事道路及新能源汽车方面的研究;董琴琴（1994-），女，四川射洪人，硕士研究生，工作于南充科技职业学院工程与应用技术学院，主要从事道路及工程机械的研究;陈作（1995-），男，重庆人，硕士研究生，工作于四川中烟工业有限责任公司成都卷烟厂，主要从事大型装备机械的研究。