时频掩码优化的两阶段语音增强算法

郑莉，李鸿燕

（太原理工大学信息与计算机学院，山西榆次 030600）

近年来，深度学习方法广泛应用在语音增强[1]中，用来解决传统语音增强方法在非平稳噪声环境下性能不稳定和泛化能力弱的问题，取得了较好的效果[2-3]。文献[4]更新了基于DNN 语音增强算法的目标函数，从而减轻估计语音的过平滑度。文献[5]同时将干净语音和干扰噪声的特征作为训练目标，利用DNN 和深度循环神经网络(Deep Recurrent Neural Network，DRNN)分别训练，相比单独对干净语音进行预测的网络结构，该方法具有更好的分离效果。文献[6]在DNN 结构中添加了具有感知掩蔽效应的部分，有效地减少了语音失真并去除了干扰噪声。以上这些研究在训练目标和网络架构的选择上各有不同，但都以均方误差作为损失函数。文献[7]在损失函数中将相邻帧网络之间进行关联，并设计感知系数反映语音存在情况，显著地提高了语音质量和语音可懂度。此外，近几年的研究工作表明，将语音幅度和相位估计结合起来有利于语音增强，相位估计可提供准确的幅度谱信息[8-9]。文献[10]验证了在提高纯净语音频谱估计中相位信息估计量发挥的显著作用。基于此，文中提出采用信噪比信息来优化损失函数的两阶段语音增强方法，利用信噪比信息计算增益系数和相位偏差，增益系数用来平衡语音失真和噪声残留之间的关系，相位偏差可以利用相位信息来更准确地预测幅度，从而优化损失函数。实验证明该优化算法可有效提高语音可懂度，增强语音质量。

1 常规深度神经网络语音增强算法

传统的基于深度神经网络的语音增强算法[5]如图1 所示，该方法分为训练和增强两个阶段。在训练过程中，将纯净语音和背景噪声叠加，生成带噪语音，并提取带噪语音的特征用于DNN 训练，在语音增强训练任务中，逐步进行有监督地调优，时频掩码[11]作为网络学习的隐目标，通过使用DNN 网络估计该掩码，然后将估计的掩码应用于带噪语音幅度谱特征，得到纯净语音幅度谱特征估计，最终网络优化的目标是该估计纯净语音幅度谱与参考干净语音幅度谱之间的均方误差。损失函数定义如下：

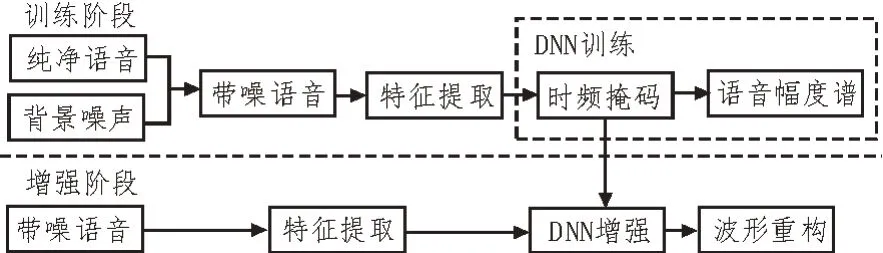
图1 常规深度神经网络语音增强算法框图

其中，Yt表示第t帧的输入带噪语音幅度谱，ft代表时频掩码函数，ft(Yt)代表预测的纯净语音幅度谱。St表示参考的纯净语音幅度谱，N代表抽取的样本数目。W、b分别是网络的权重矩阵和转置向量，利用误差反向传播算法来更新网络权值，经过一系列迭代更新，得到训练好的网络。

在增强阶段，将带噪语音输入训练好的网络，输出即为估计的纯净语音幅度谱特征，根据人耳对相位变化不太敏感这一特性，将带噪语音的相位与估计的纯净语音幅度谱合成并进行短时傅里叶逆变换，得到增强的语音信号。

2 优化的两阶段网络语音增强算法

在传统深度神经网络语音增强算法中，将语音增强作为回归任务设计损失函数，取得了显著效果，但未考虑不同信噪比时，带噪语音中语音和噪声所占比重的不同。当SNR 较低时，噪声占比较大，导致增强后语音中残留噪声能量较多，语音信息被屏蔽，语音可懂度降低；当SNR 较高时，语音占比大，增强后容易造成语音失真，导致语音质量较差。针对此问题，文中提出利用信噪比信息优化损失函数的两阶段语音增强算法[12]。第一阶段从带噪语音中初步预测纯净语音幅度谱和噪声幅度谱，用来提供SNR信息；第二阶段，利用SNR 信息生成增益系数和相位偏差，优化时频掩码函数，输出增强的语音幅度谱。训练阶段算法框图如图2 所示。

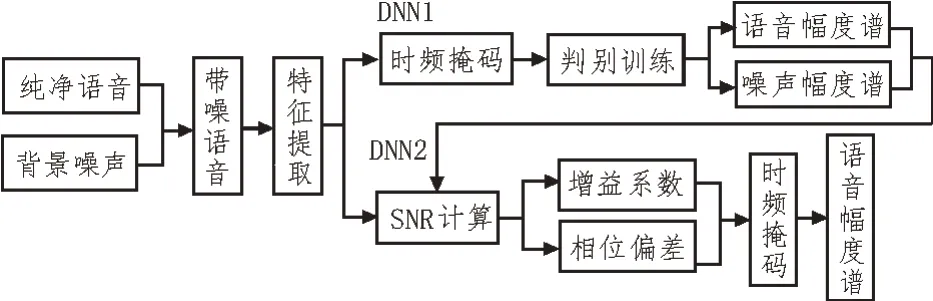
图2 时频掩码优化的两阶段语音增强算法框图

2.1 信号模型

在实际中，同时测得带噪语音和纯净语音比较困难，因此通过叠加来获得目标带噪语音，用y(t)、s(t)、n(t)分别表示t时刻生成的带噪语音、纯净语音以及不相关的背景噪声，则带噪语音可以表示为纯净语音信号及其不相关的背景噪声的叠加。用以下模型来表示带噪语音：

2.2 特征提取

语音信号在非特定范围内是非平稳时变信号，截取其10～30 ms 范围内的短时平稳状态，对式（2）作短时傅里叶变换，得到频域中的噪声表示如下：

其中，Y(t，f)、S(t，f)、N(t，f)分别表示带噪语音、纯净语音和背景噪声在第t帧、第f频带的频谱分量，通过设置不同α得到目标信噪比的带噪语音。

2.3 DNN1阶段

对于给定的带噪语音，该阶段对语音谱和噪声谱同时建模，将带噪语音的幅度谱特征输入网络，将纯净语音和噪声的幅度谱作为参考目标，最终输出估计的语音幅度谱和噪声幅度谱，定义时频掩码函数：

在损失函数中添加参数γ，通过网络训练来提高语音预测准确度。假设语音和噪声相互独立，同时最小化语音与预测语音、噪声与预测噪声之间的均方差，最大化语音与预测噪声、噪声与预测语音之间的均方差。损失函数定义为：

2.4 DNN2阶段

该阶段利用信噪比信息计算增益函数和相位偏差来共同优化时频掩码函数，参与网络训练过程，最终生成纯净语音幅度谱。

2.4.1 增益系数

为了减小语音失真，引入滤波函数[13]，最小化语音失真同时将残留噪声限制在某一预设阈值水平下，定义为：

其中，δ代表预设阈值，用于限制噪声强度；μ代表增益系数，用于控制语音失真和残留噪声之间的平衡。

H(w)的第k个对角元素H(wt)为：

根据以下分段函数计算可得到μ的值，SNRdB=10 log10SNR；μt是由实验计算得到的最佳值，μ0=(1+4μt)/5；k=25/(μ0+1)。

2.4.2 相位偏差

相位偏差定义为φdev=φy-φs，即带噪语音相位与纯净语音相位之间的差异，相位偏差取决于信噪比[14]，利用信噪比信息可计算得到相位偏差。由几何三角关系式变换可得到相位偏差公式如下：

其中，φns=φn-φs，φn、φs分别代表背景噪声的相位和纯净语音的相位，由几何关系式可得到Y2=S2+N2+2SNcosφns，求解cosφns，可得：

2.4.3 损失函数

使用增益系数和相位[15]偏差来优化最初的时频掩码函数ft：

损失函数定义为：

其中，Y(wt)表示第t帧的输入带噪语音幅度谱，ft表示时频掩码函数，ft(Y(wt))表示预测的纯净语音幅度谱。St表示参考的纯净语音幅度谱，N代表小批量样本数目。利用误差反向传播算法来更新网络权值，网络经过一系列迭代更新，得到训练好的网络。

3 实验仿真

3.1 实验设置

采用TIMIT语料库中的纯净语音数据，选取10个说话人，男女各5 人，每人10 条语音，共100 条语音，从Noisex-92 噪声库数据中选取5 种噪声，将语音和噪声按照不同信噪比（-5，0，5）随机挑选一种，共合成500 条带噪语音，选取400 条作为训练集，100 条作为测试集。语音和噪声的采样频率均为16 kHz，使用64 ms 的汉明窗和32 ms 的窗移对信号进行分频，幅度谱作为网络的输入特征，对于每个时间帧，采用具有50%重叠的1 024 点短时傅里叶变换提取频谱表示，得到512 维幅度谱特征。

在DNN 训练中，将输入数据归一化为零均值和单位方差，激活函数选择relu 函数。网络中包含隐藏层2 层，每个隐藏层中有1 000 个隐藏单元，输出层有1 026 个单元。网络采用随机初始化，使用L-BFGS 梯度下降法，minibatch 的大小为100，训练网络总的迭代次数设置为20 次。

3.2 评价指标

为了比较文中算法的语音增强性能，采用语音质量感知评估(Perceptual Evaluation of Speech Quality，PESQ)指标和短时客观可懂度(Short Time Objective Intelligibility，STOI)指标对不同方法增强后的语音进行评价。PESQ 用来比较干净参考信号和分离信号的响度谱，其得分范围为(-0.5 4.5)，得分越高，语音质量越好；STOl 主要用来衡量干净语音和单独话语的短时时间包络之间的相关性，其得分范围为(0 1)，可以理解为正确的百分比，得分越高，语音可懂度越好。

3.3 实验结果及分析

将文中所提算法与传统算法进行对比，为了保持相同的网络深度，均使用具有4 个隐藏层的DNN，特征提取和参数设置均一致。使用语音质量感知评估指标和语音可懂度指标对增强语音进行评价，对比结果如表1 所示。语音信号的波形图和语谱图可以显示去噪的细节信息，图3 给出了在-5 dB Train 噪声时纯净语音、带噪语音、优化前算法以及文中所提算法处理的时域波形图，图4 给出了两种算法的语谱图。

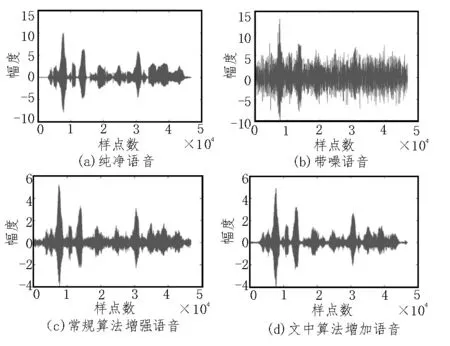
图3 不同算法增强语音的波形图

图4 不同算法增强语音的语谱图

表1 语音可懂度与语音质量评估结果

对比图3、图4 可以看出，优化前算法保持了较好的语音结构，但仍存在不少残留噪声；改进的语音增强算法不仅能保持语音信号的谐波结构，减少语音失真，而且更加有效地去除了低频残留噪声，使增强后语音波形更接近纯净语音波形。另外，表1 结果表明，文中提出的算法增强后语音的感知质量评估指标和可懂度在各种信噪比及不同的背景噪声下均有提高，与优化前算法对比，语音质量感知评估指标平均提高了0.22；语音可懂度评估指标平均提高了0.027。尤其是在-5 dB 低信噪比条件下，各种噪声下的增强语音质量和语音可懂度均有较大幅度提升，表明所提改进算法可以去除残留噪声，减少语音失真并较好地重构语音。

4 结束语

文中提出利用信噪比信息优化时频掩码函数的两阶段语音增强算法，利用DNN 估计信噪比信息，通过引入增益系数，最大程度减小增强后语音的失真并尽可能地去除残留噪声；同时引入带噪语音和纯净语音的相位偏差信息来提供更准确的幅度谱信息。通过对不同信噪比下噪声进行的实验验证表明，该算法有很好的增强效果，尤其是在低信噪比条件下，能够较好地去除噪声并保留语音结构。