一种改进的模逆算法与硬件实现

胡锦，李勇彬

（湖南大学物理与微电子科学学院，湖南长沙 410082）

RSA 密码和椭圆曲线密码是目前使用最广泛的公钥密码算法.随着物联网的发展，用户信息安全越来越重要，例如现今高速发展的智能汽车，安全性和实时性要求极高，软件实现加密算法的方式已经无法满足需求，采用硬件方式实现算法是发展的趋势.模逆算法是公钥密码体系中的核心算法［1-2］，尤其在椭圆曲线密码体系中［3］，也是最复杂［4］和最消耗时间的算法之一［5］.在RSA 密码算法中，生成密钥对时，需要计算d=e-1modφ，其中e表示公钥，满足1＜e＜φ且gcd（e，φ）=1，φ表示欧拉函数，d表示私钥.为了安全，φ至少为1 024 位，用软件实现模逆运算，运算量大，运算时间长，效率低［6］.在椭圆曲线密码算法中，进行点加［7］、点乘和倍点运算时，用雅可比坐标进行坐标变换［8］也只能减少模逆运算使用的次数而不能完全避免.本文在现有的二进制模逆算法基础上进行了改进，提出了一种在求逆过程中同时可以求取最大公约数的算法.此外，出于对实现算法的硬件资源考虑，对算法做了优化，最后通过VERILOG 语言进行硬件实现.

1 算法介绍

1.1 二进制模逆算法

二进制模逆算法原理是根据贝祖等式gcd（a，b）=gcd（b-a，a）=ax+by 推导得出.目前常用的模逆算法还有扩展欧几里得算法［9-10］，但是由于算法中每步都要用到除法操作，开销很大［11］，尤其在进行大素数模逆运算时缺点更突出.算法1 只用到了移位操作和减法运算，比扩展欧几里得算法更加高效.

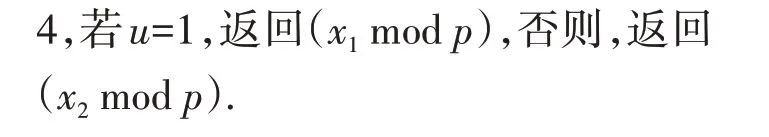
1.2 改进的模逆算法

算法1 有一个缺陷是无法判定输入的两数是否互质，如果gcd（a，p）不等于1 时，再用算法1 计算就会得到错误的结果，或者说算出的结果是没有意义的.结合stein 算法［11］，可以将上述算法改写为算法2，算法2 在模逆运算的同时可以求解最大公约数gcd（a，p），从而保证模逆运算的结果是在gcd（a，p）=1 的情况下得到的正确结果.在算法1 中可以看出，循环计算时u和v的计算基本上是一致的，为了节省资源，可以进行进一步优化.由于算法2 中的步骤3和步骤5.2 保证u和v每次循环最多只有一个为偶数，利用这个特点可以去掉u的循环.

2 算法硬件结构框图

模逆算法主要通过状态机来控制算法流程，通过ram 存储大量的中间数据，图1是模逆算法硬件结构框图，主要分为两个模块，INV_FSM 模块是状态机模块，INV_CAL是模逆算法的运算模块，受状态机模块的调度.ram 为伪双端口ram，主要用来存储在运算过程中产生的中间数据和运算结果.

图1 模逆算法硬件结构框图Fig.1 Modular inversion algorithm hardware structure block diagram

2.1 算法状态机

图2 是模逆算法的状态转移图，严格控制模逆算法的运算流程.该状态机共有9个状态，IDLE是空闲状态，开始运算时，进入SHIFT状态，SHIFT状态完成x和y同时向右移位（即除以2），g向左移位，直到x和y不同时为偶数.LOAD 状态主要完成u、v、A、B、C、D数据的装载.INV_CAL 状态完成模逆算法的主体运算直到v等于0 时才跳出该状态.在GCD_CAL状态中完成gcd（a，p）计算，在GCD_CAL 状态计算完成后判断A的极性进行状态跳转.若A为负数，则跳转到A_NEG 状态进行A+y运算，直到A为正数，则跳转到DONE状态；若A为正数，则跳转到A_POS1状态进一步判断A是否大于y，若A小于y，则跳转到DONE 状态，若A大于y则跳转到A_POS2 状态进行A-y运算，直到A小于y，然后跳转到DONE 状态，模逆运算完成，最终回到IDLE状态.

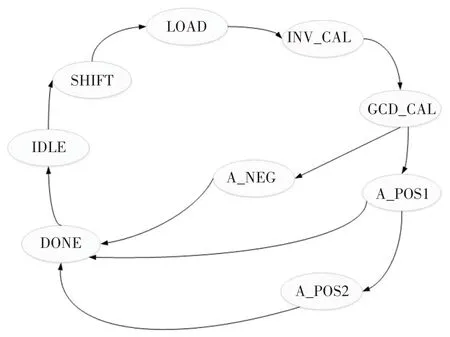
图2 模逆算法状态转移图Fig.2 State transition diagram of modular inversion algorithm

2.2 算法运算模块

算法运算模块主要功能是在状态机的控制下进行数据的运算.从算法2 中可以看出，求逆的过程需要用到大数加法和大数减法，还需要进行两数大小判断和移位.大数加法和大数减法可以通过算法3和算法4 实现，两数的大小比较可以通过使用大数减法的借位信号来判断.图3 是运算模块主要运算电路，data_v和data_u通过mux 来进行选择，mux 的选择信号通过比较data_u和data_v的大小得到，data_c和data_a、data_b和data_d类似.从图3 中可以看出：改进后的算法使用mux 可以进行u和v的选择，从而实现资源的复用，减少了资源的消耗.运算的中间结果和运算结果保存在ram中.

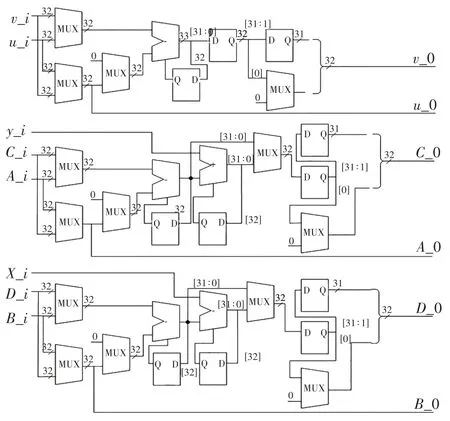
图3 算法模块电路图Fig.3 Algorithm module circuit diagram

该电路中输入数据都是以32 位为最小输入单元，如果进行1 024 位的模逆运算，此电路需要计算32 次，可以看出此电路其实还可以实现2 048位甚至更大的模逆运算.需要注意的是.计算的位宽越大，需要保存的中间数据也越多，ram的容量就需要越大.

3 结果与分析

通过VCS 对该电路进行功能仿真，如图4 所示.模逆算法电路能正确计算出最大公约数和模逆运算的结果，将计算的结果保存在ram 中.仿真结果表明：该设计可以正确进行32～1 024 bit的模逆运算.

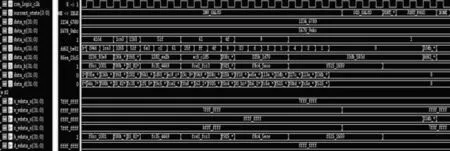
图4 算法功能仿真图Fig.4 Algorithm function simulation diagram

使用Xilinx virtex-II FPGA 开发板进行了板级验证，验证了该设计的正确性.表1 列出了该设计与同类设计的资源消耗和性能比较.表格中的时间为计算256 bit模逆运算使用的时间.

表1 FPGA结果对比Tab.1 FPGA result comparison

该设计应用于一款汽车安全芯片的PKI 模块，用于实现RSA 和SM2 算法.图5 为该安全芯片的版图，采用UMC 55 nm 工艺进行流片，该芯片总面积为10 mm2，在工作电压3.3 V，时钟频率为200 MHz 时，功耗仅为30.2 mW，流片测试结果表明，芯片达到设计指标要求.

图5 芯片版图Fig.5 Chip layout

4 结语

本文提出了一种在现有二进制模逆算法的基础上进行改进的算法.该算法不仅可以进行模逆运算，还同时可以计算最大公约数，并且在算法上进行了优化，减少了算法实现的资源消耗，最后通过VERILOG 语言实现了该算法.该设计电路结构简单，可扩展性强.最后该设计采用UMC 55nm 工艺进行流片，流片测试结果表明，芯片达到设计指标要求.