浅埋软土地层盾构推进速度预测模型的建立与选择

潘腾飞

（山西应用科技学院，山西 太原 030062）

0 引言

本文依托某市轨道交通盾构工程，采用多元线性回归分析方法考虑“力学参数影响因子（土压力、推力、刀盘扭矩）”和“机械参数影响因子（螺旋机转速）”对盾构推进速度的单因素作用和两者协调作用的影响，建立了浅埋软土地层盾构掘进速度4种预测模型，并将该预测模型用于本工程盾构推进速度的预测。通过将预测值与实际监测值对比分析，得到了在满足施工要求精度的前提下，考虑单一因素“力学参数影响因子”以及综合考虑“力学参数影响因子”、“机械参数影响因子”的盾构推进速度预测模型。该研究方法及研究成果具有较好的科研价值和工程实践意义。

1 推进速度影响因素分析

在盾构法隧道施工中，影响盾构机推进的参数较多，推进参数的选取不仅要体现不同影响因素的作用，并且还要考虑具体的施工条件。一般来说，在施工中，影响推进速度的参数主要有土压力（P）、推力（F）、刀盘扭矩（T）、螺旋机转速（r）等。由于土压力（P）、推力（F）、刀盘扭矩（T）均属于力学参数，本文将其称为“力学参数影响因子”，而螺旋机转速（r）属于机械参数，将其称为“机械参数影响因子。”

本文将展开关于“力学参数影响因子”和“机械参数影响因子”对盾构推进速度的单因素影响和两者交互影响的相关研究，建立基于各影响因子下的盾构推进速度预测模型。

2 推进速度预测模型

2.1 推进速度预测模型的建立

（1）数据选取及预处理。为分析盾构推进速度进行分析，采集了该线路1457份盾构施工参数来进行研究，每一份样本均包括土压力（P）、推力（F）、刀盘扭矩（T）、螺旋机转速（r）4个参数。运用正态分布函数，对所选取的预测变量数据样本分布状态进行分析，分析结果如图1所示。

由图1可知，推进速度在37～66mm/min之间的数据样本较为集中，约占数据样本的97%，故本次选用该区间数据作为分析对象进行研究，并利用公式，对所选数据进行标准化处理。最后，按照正态分布函数拟定推进速度分布区间对其进行分组，并对各组数据进行平均化处理。

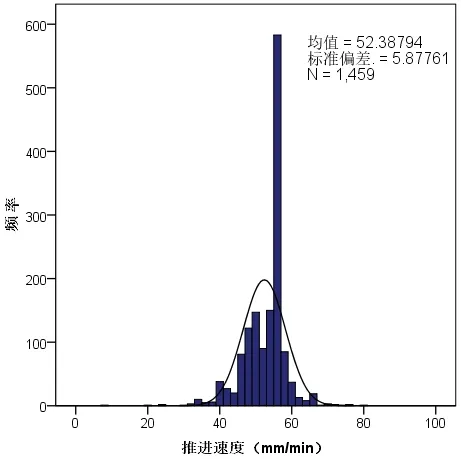
图1 推进速度样本分布状态

（2）多元线性回归分析。根据分析因素的不同及自变量形式的差异，本文拟建立4种盾构隧道推进速度预测模型，如表1所示。

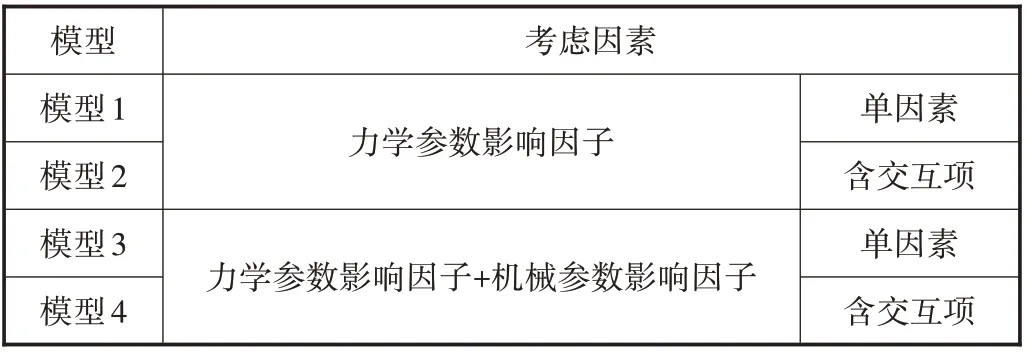
表1 拟建预测模型

根据上述数据预处理结果，利用统计学软件SPSS（Statistical ProductandServiceSolutions），分析并建立关于推进速度v、土压力P、推力F、刀盘扭矩T的多元线性回归模型。

①模型1：

②模型2：

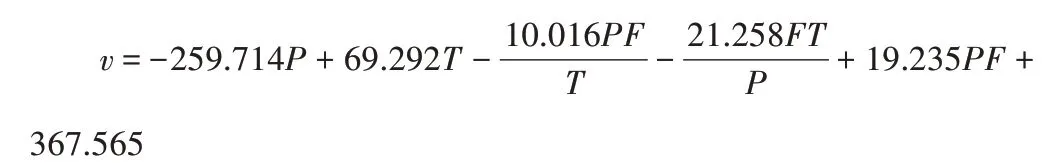
③模型3：

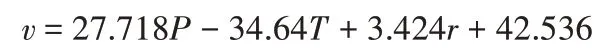
④模型4：

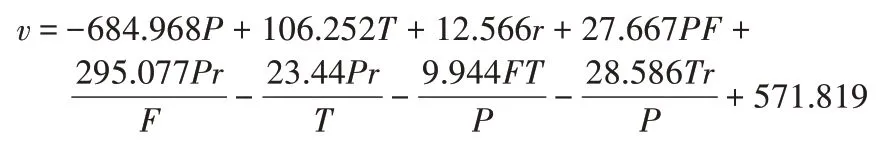
式中：

v——推进速度，mm/min；

F——推力，MN；

T——刀盘扭矩，MN·m；

P——土压力，bar；

r——螺旋机转速，r/min。

综上所述，运用多元线性回归分析模型，建立了4种软土地区盾构隧道推进速度预测模型，如表2所示：

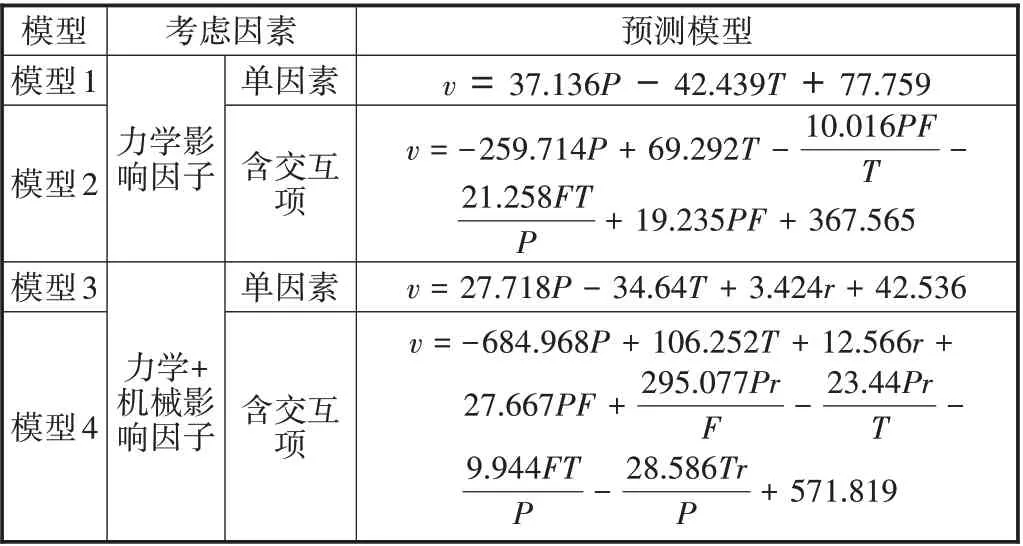
表2 软土地区盾构隧道预测模型

2.2 推进速度预测模型合理性验证

根据模型合理性评价指标对上述建立的4种预测模型进行合理性验证，为了排除人为因素、随机因素对参数的影响，运用正态分布函数，对各自变量参数区间进行分析，限于篇幅原因，以推力和刀盘扭矩为例，如图2所示，根据正态分布分析，按照95.45%的置信区间进行岩本选取，最终从原始样本中选取了1420份数据用于后续的模型合理性检验。

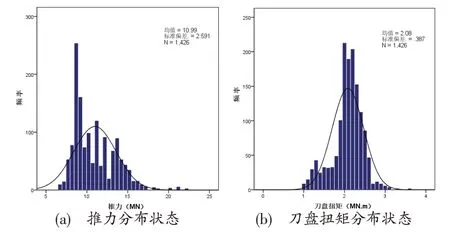
图2 各参数分布状态

利用选取的参数区间，对模型预测值的误差进行计算，进而对误差区间进行分析对比，确立了相应的误差正态分布函数，如表3所示。

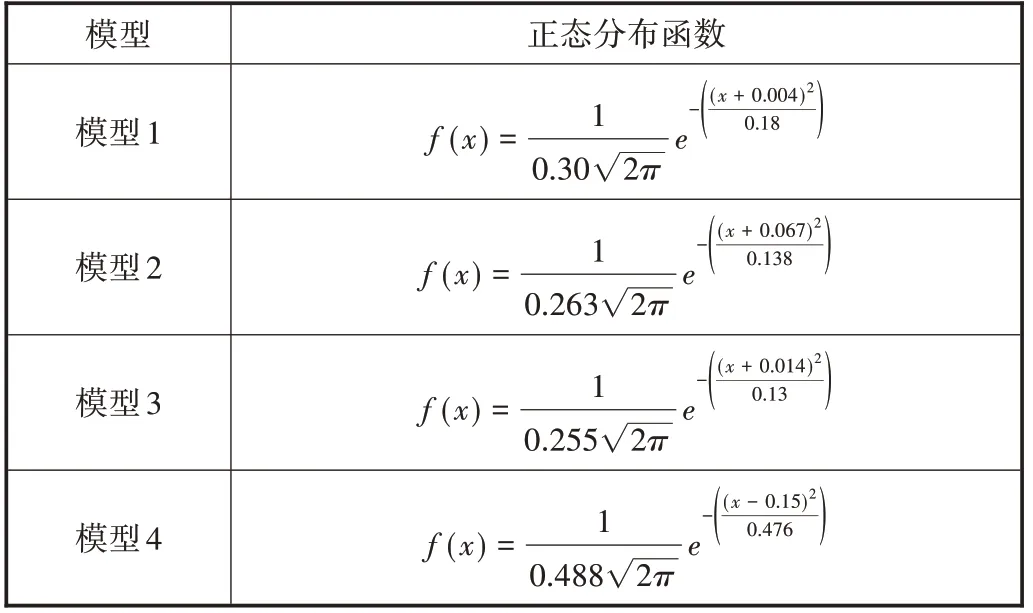
表3 各模型误差正态分布函数表

2.3 选择最佳的预测模型

根据误差正态分布函数，求取误差为5%、10%、15%、20%、25%、30%条件下的样本占比，如表4所示。

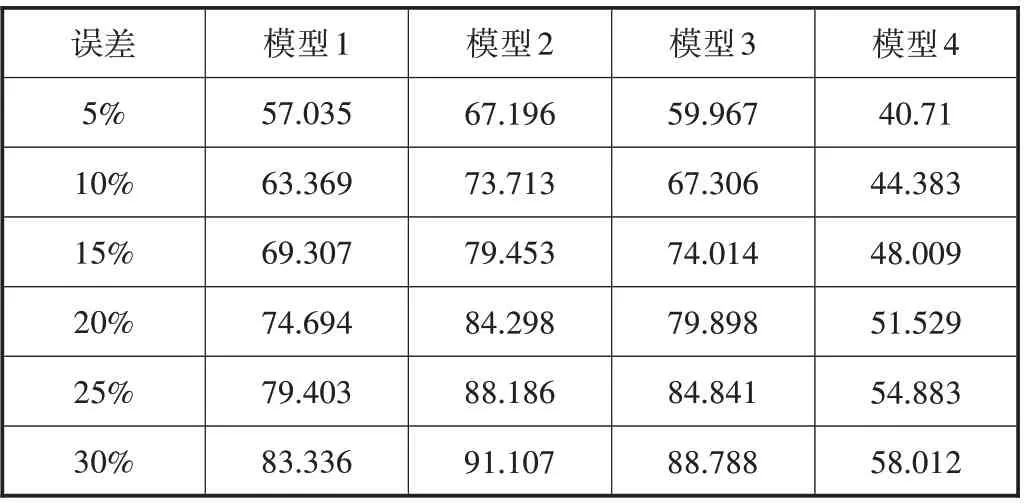
表4 各误差下的样本占比 %

由表4可知，当误差为5%时，模型1、2、3、4的样本占比分别为57.04%、67.2%、59.97%、40.71%；当误差为10%时，模型1、2、3、4的样本占比分别为63.37%、73.71%、67.31%、44.38%；当误差为15%时，模型1、2、3、4的样本占比分别为74.69%、84.30%、79.90%、48.01%；当误差为20%时，模型1、2、3、4的样本占比分别为74.69%、88.19%、84.84%、54.88%；当误差为30%时，模型1、2、3、4的样本占比分别为83.3%、91.11%、88.79%、58.01%。

综上所述，当误差为20%时，选用模型2、3样本占比能达到88.19%、84.84%，即当只考虑力学参数影响因子时，选用模型2对推进速度进行预测，精度可达到88.19%，当考虑力学参数影响因子及机械参数影响因子时，选用模型3对推进速度进行预备，精度可达到84.48%。

3 结束语

本文依托某市轨道交通盾构施工实测数据，采用多元线性回归分析方法，考虑“力学参数影响因子（土压力、推力、刀盘扭矩）”和“机械参数影响因子（螺旋机转速）”对盾构推进速度的单因素作用和两者协调作用的影响，并运用多元线性回归分析方法，建立了关于力学参数影响因子（土压力、推力、刀盘扭矩）的盾构隧道推进速度的2种预测模型，及关于力学参数影响因子+机械参数影响因子的盾构隧道推进速度2种预测模型，共计4种计算模型。

最终，通过模型合理性验证方法，利用各模型的误差正态分布函数分析了各模型的误差分布状态，并给出了不同误差条件下推进速度预测的可靠性。通过4种预测模型的对比分析，最终给出了精度较高的2种预测模型来应用于实际，即当只考虑力学参数影响因子时，选用模型2对推进速度进行预测，精度可达到88.19%，当考虑力学参数影响因子及机械参数影响因子时，选用模型3对推进速度进行预测，精度可达到84.48%。