多层典型钢筋混凝土框架结构易损性分析及抗震性能研究

陈 双（广安职业技术学院，四川 广安 638000）

随着城镇化的不断发展，城市抗灾能力成为城市存续与发展的主要问题之一，只有具备较强的城市抗灾能力才能对居民的生命以及财产安全提供保障[1]。在城市风险因素中自然灾害的风险占据了极大比例，地震灾害即是其中破坏力较强的一种，因此，基于可靠理论的震损工程评估与优化加固研究具有重要的现实意义[4-6]。目前，针对多层典型钢筋混凝土框架结构的研究取得了很多成果，诸如利用高烈度区框架梁的弯矩分布的特殊性设计框架梁、结合多层钢筋混凝土框架结构，对“加层减震”能量时程进行分析，通过分析多层钢筋混凝土框架结构的框架柱震害案例，对框架柱梁抗弯能力比值以及柱轴压比等抗震指标进行研究等。不过相关领域仍遗留了许多亟待解决的问题，本次研究将从需求能力角度入手，对多层典型钢筋混凝土框架结构的易损性及抗震性能进行研究。

1 多层典型钢筋混凝土框架结构易损性及抗震性能研究

1.1 多层典型钢筋混凝土框架结构易损性能力需求模型的建立

多层典型钢筋混凝土框架结构(Reinforce concrete con⁃struction)简称RC框架结构。对RC框架结构的地震易损性分析(Seismic Fragility)是指在已知地震强度下分析框架结构超越固定极限状态的概率，防止由于结构、材料、外部因素等不确定性因素的叠加导致的意外偏差[2]。

在分析过程中，应考虑结构在形变过程中是否维持平面、应力是否均匀分布、钢筋与混凝土之间是否出现滑移等多种因素的影响，其中包含一部分确定性因素，但也包含大量不确定性因素。不确定性因素主要由两大部分组成，一部分是建筑结构自身产生的不确定性，这一部分因素大部分在施工建设以及建筑养护过程中出现，例如建筑师的设计因素、施工的质量控制因素，养护条件因素等[3]。另一部分是有限元建模技术产生的不确定性，例如非线性单元因素、材料参数因素等，可将其根据材料结构进行划分，大致区分为钢筋材料的不确定性、混凝土材料的不确定性、结构粘滞阻尼的不确定性[14-15]。在分析过程中应将确定因素与不确定因素一并进行充分考虑。将地震易损性以框架结构失效概率的形式进行转换可得公式：

式中Pf表示失效概率，D表示结构地震需求，C表示规定极限状态，IM表示地震动强度参数，x表示地震动强度水平。在此假定地震需求参数与地震动强度存在关系：

式中EDP表示地震需求参数，而地震响应中位值与地震动强度同样存在关系：

式中，此时假定公式(1)中的与两个变量均是随机且独立的，那么结构失效概率可以通过推导得出，如公式(5):

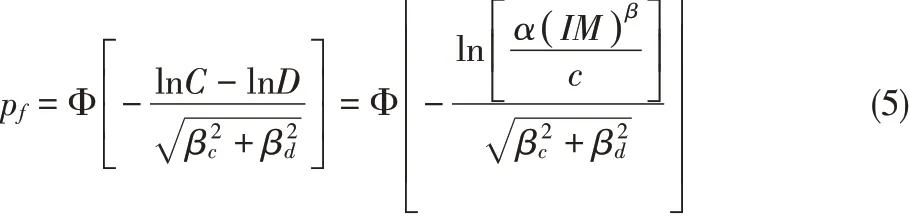
式中Φ表示标准正态分布函数，C表示结构能力中位值，βd与βc表示变量D与C的标准差。

1.2 多层典型钢筋混凝土框架结构抗震性能评估方法

由于地震的随机性以及震动对建筑结构的影响具有不确定性，RC框架结构的抗震性能往往并不是恒定的，根据应力变化结构自身的应变也会区分为不同情况。因此，在进行评估时，需要从概率角度对整体结构的可靠性进行分析。本次研究根据大震不倒、中震可修、小震不坏的原则从需求能力方面对抗震性能进行分析。需求能力系数法可以表示为：

式中F.D.表示结构抗需求，F.C.表示结构抗震能力，数学表达式可进一步写为：

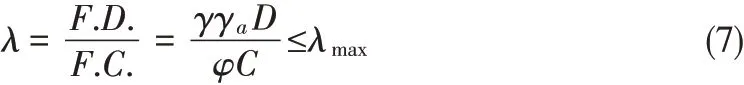
式其中λ表示表征结构的可靠性参数，γ表示表征结构的地震需求不稳定性系数，γa表示内在偏差以及不确定系数，φ表示结构能力不确定性系数，D表示层间位移角中位值的估计值，C表示表征结构地震相应参数中位值的估计值。为表示地震过程中产生的结构不确定性与随机不确定性，结构地震需求可以表示为：而结构抗震能力则可以表示为：

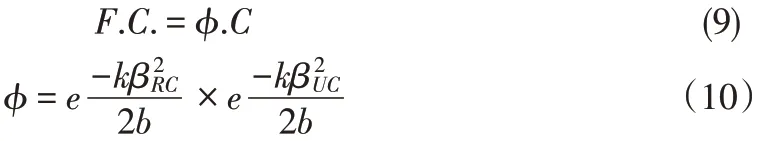
式中R表示随机性，U表示不确定性，C表示能力，RC表示能力随机性，UC表示能力不确定性，k表示地震危险性曲线的斜率，b表示结构能力改变和地震动强度参数改变的相关系数。在需求能力系数法的实现过程中，主要需要考虑的工作包括4个方面，分别为结构地震需求的分析、结构地震能力的分析、不确定性的分析以及根据不同性能标准下的置信概率的分析。在分析过程中需要选定对应的地震设防水准，并以工程现场特质为根据在地震数据库中选定数条天然地震记录。将不同性能目标区分开后，便可以针对不同目标下结构框架的抗震能力进行计算，为进一步的定量分析提供依据。

2 多层典型钢筋混凝土框架结构易损性及抗震性能评估分析

2.1 多层典型钢筋混凝土框架结构易损性评估分析

本次研究针对多层典型钢筋混凝土框架结构的易损性及抗震性能进行分析，分为易损性分析与抗震性能分析两部分，并利用实际案例数据进行佐证。在易损性部分则分为超越破坏极限概率对比以及易损性对比两部分，针对不同地震等级下超越破坏极限概率的对比，分为2D模型与3D模型两部分进行分析，在4种破坏水平与3种地震烈度下，超越破坏极限的概率的趋势，基本维持了随着地震烈度的增加而增加的趋势。且2D模型的超越破坏极限概率普遍稍大于3D模型的超越破坏极限概率，这是因为2D模型仅有平面内的3个自由度，而3D模型则拥有空间内的6个自由度。因此2D模型的破坏只能是发生在平面内的扭转与平移，3D模型却可以产生以纵向轴为主轴的运动，并且在立体空间中楼板之间的协同作用也能得到充分考虑。两种模型均能达到分析易损性的效果，但3D模型要更加适用。

接下来实际将模型应用到易损性分析之中去，根据确定性参数与不确定性参数将结构模型，分为确定性结构与不确定性结构两部分，根据实验数据在不确定性因素与确定性因素的对比中，无论哪种等级的破坏程度确定性结构的超越概率曲线走势都更低，均位于不确定性结构的超越概率曲线的下方，可见同一地震等级下确定性结构，超越当时极限状态的概率要比不确定性结构的概率更小。破坏程度逐渐上升的情况下，确定性结构与不确定性结构之间的曲线差异逐渐增大，说明结构模型自身的不确定性，对于结构易损性的影响是随着地震破坏程度的提高而不断增大的。而针对不同地震程度的对比可以发现，在小震的情况下确定性结构处于破坏程度1级的概率高于不确定性结构，分别为48.9%对比37.8%，而其他破坏等级的概率均低于不确定性结构，可见在小震情况下确定性结构更加稳定，破坏基本集中在最为轻微的1级破坏部分。在中震情况下，确定性结构在1级与2级破坏等级处的概率仍旧高于不确定性结构，分别为3.1%对比1.6%、28.2%对比20.9%，而3级与4级破坏等级处的概率则更低，可见在中震情况下确定性建筑仍旧更加稳定，主要破坏集中在较为轻微的破坏水平之下。在大震情况下，确定性结构在1、2以及3级破坏等级处的概率都更高，而较为严重的4、5级破坏出现的概率则更低，分别为61.6%对比66.1%、6.5%对比10.2%，可见在大震情况下确定性结构仍旧更加稳定。

2.2 多层典型钢筋混凝土框架结构抗震性能评估分析

在抗震性能分析部分，本次研究从总体结构不确定性、结构地震能力需求比以及置信水平与置信概率三个方面进行分析，而在置信概率方面则根据小震标准50%，中震标准75%，大震标准90%的标准进行衡量（详见表1）。

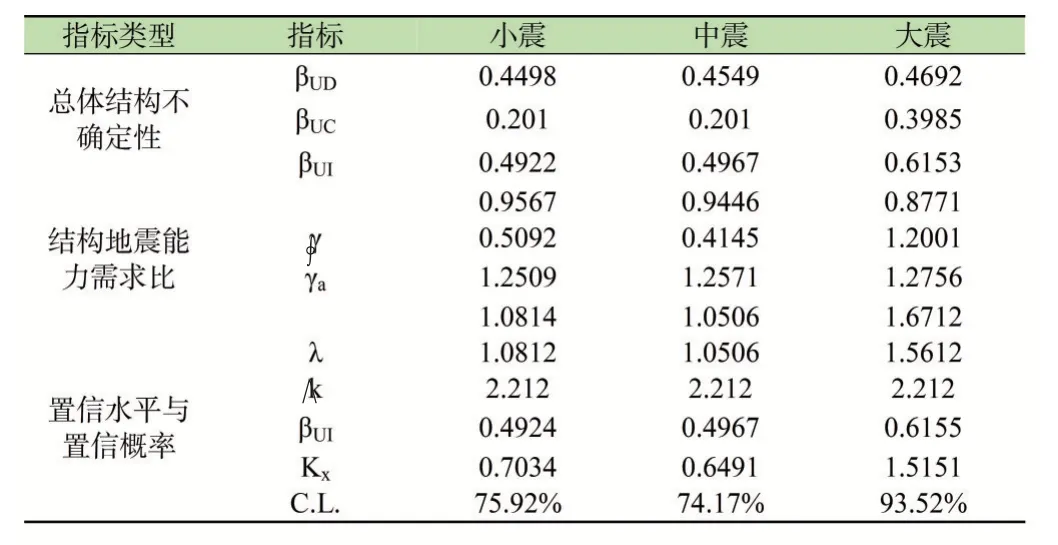
表1 抗震性能评估指标

如表1所示，小震情况下Kx置信水平的数值为0.7034，而中震情况下Kx置信水平的数值最小为0.6491，大震情况下Kx置信水平的数值最大为1.5151。置信概率C.L.的最高值同样出现在大震情况下，数值为93.52%，小震情况下的置信概率C.L.数值次之，最小值出现在中震情况下，数值为74.17%。由此可见在小震情况下置信概率为75.92%，远大于标准值的50%，满足小震不坏的目标；中震情况下置信概率为74.17%，虽然没有达到75%，但是极度接近目标，基本达到了中震可修的效果；而在大震情况下置信概率为93.52%，高于标准值的90%，达到了大震不倒的效果。

3 结语

建筑结构整体在地震环境下的可靠性与安全性，一直是建筑工程领域重要的研究课题。本次研究从多层典型钢筋混凝土框架结构的特性与损坏因素入手，针对易损性建立易损性能力需求模型，并将其实际运用到易损性分析中去，从确定性与不确定性、2D与3D两方面对模型进行评估。针对抗震性能则从大震不倒、中震可修、小震不坏的原则出发，利用置信概率对结构模型的抗震性能进行评估。结果显示小震情况下确定性结构处于破坏程度1级的概率高于不确定性结构，而其他破坏等级的概率均小于不确定性结构；中震情况下确定性结构在1级与2级破坏等级处的概率高于不确定性结构，3级与4级破坏等级处的概率低于不确定性结构；中震情况下确定性结构在1、2以及3级破坏等级处的概率都更高，而较为严重的4、5级破坏等级出现的概率则更低。可见在不同的地震程度下确定性结构的破坏程度，普遍小于不确定结构的破坏程度。在抗震性能方面小震情况下置信概率远大于50%的标准，数值为75.92%；中震情况下置信概率虽小于75%的标准，但是极度接近标准，数值为74.17%；大震情况下置信概率大于90%的标准，数值为93.52%。可见在3种地震程度下建筑结构的抗震性能均高于标准，抗震效果较好。