黏弹性人工边界在地下结构抗震分析中的应用

迟 恒，王寿生，王 维

[上海市政工程设计研究总院（集团）有限公司，上海市 200092]

0 引言

城市地下结构,尤其是隧道、地铁、地下车站、地下管线系统,是现代社会公共基础设施的重要组成部分。考虑到城市地下结构对经济及生命安全的重要性,对地下结构进行抗震安全设计是必要的。依据《地下结构抗震设计标准》（GB/T51336—2018）要求，对于地质条件复杂（如：含软弱、液化土层）且结构体型复杂的地下结构应进行弹塑性时程分析进行抗震安全评估。而地震时地下结构-土体相互作用是在无限域的场地中进行，如何近真实地动态模拟场地边界成为分析结果可靠性的难点之一。图1为广义结构与远场岩土之间设置虚拟人工边界的整体计算模型[1]。

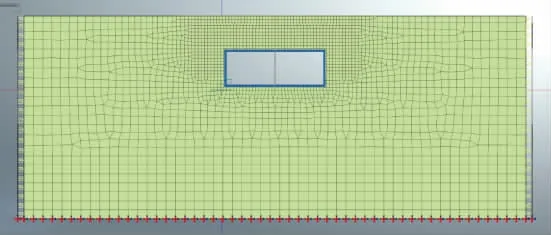
图1 结构-场地动力计算模型

在无限连续土层介质中采用虚拟边界进行有限化模拟，即构建人工边界。在无限域的场地模拟人工边界不仅需满足边界设置要求条件,且可真正模拟无限域场地动力特性。其土的力学分析上人工边界为近场波动对应的偏微分方程。人工边界条件的真实性为是否能准确模拟对无限域连续介质场地,即地震波在人工边界处的传播特性与无限域连续介质保持统一。从近场任何方向入射的地震波通过设置的黏弹性人工边界时无反射效应,即波在人工边界处被边界完全吸收，或完全透射。通常人工边界也被认为是无反射、透射或吸收的有限域边界[2]。在地下结构抗震分析中，人工边界条件对无限域模拟的准确与否将直接影响近场波动数值模拟的精度,因此人工边界条件的研究具有重要意义[3]。图2为ANSYS场地分析模型。

图2 ANSYS场地分析模型

1 黏弹性人工边界基本理论

Deeks等人提出假定二维散射波以柱面形式向外发散，模拟了黏弹性人工边界。此后黏弹性人工边界模型受到了国内外众多学者的关注，其中刘晶波等人做了大量的研究工作，例如，基于柱面波动方程建立了二维黏弹性人工边界[4]；并以球面波动方程为基础提出了三维黏黏弹性人工边界[9]；依据半无限空间中的静力问题基本解构造出黏弹性静动力统一人工边界以及方便工程应用的二维、三维一致黏弹性人工边界与等效黏弹性边界单元，并就人工边界的波源问题和地震波动输入问题进行了系统性的讨论，从而实现对实际连续介质应力边界条件的模拟[5]。

此外，L.Kellezi在黏弹性人工边界的研究中引入了波动入射角度概念，对各入射角度赋予不同边界参数，取得了较好的效果。然而，人工边界是针对某种固定形式的外行波设置的，在近场地基地形和地质条件均较复杂下会产生各种的散射波形式，以致使边界对外行波的吸收不充分而产生误差，那么在复杂地基条件下此类边界模型的计算结果是否在工程精度要求将成为一个有待研究的课题。

1.1 黏弹性边界的一般表达式

黏弹性人工边界可表达为连续分布且相互偶联的耗能弹簧-阻尼器，拟设人工边界上法向及切向弹簧刚度和阻尼系数可按下列公式取值[6]：

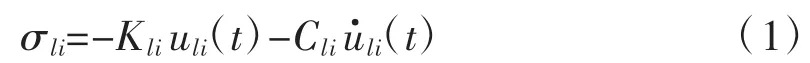
式中：l为人工边界节点号；i=x，y，z代表分量方向；t表示时间；σli，uli，为节点方向的应力、位移和速度；Kli，Cli为节点方向的黏弹边界参数。

1.2 边界节点运动方程

为真实模拟有限域边界，考虑无限域动力特性的黏弹性有限边界表达时，边界节点动力方程可表达为：

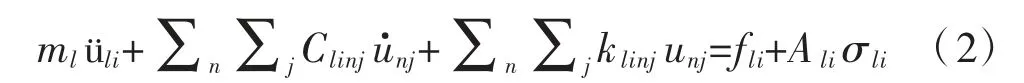
式中：σli为黏弹性边界处节点l应力为节点l应力的作用范围；N为与节点震动关联的单元数；Ale为单元e上黏弹边界的作用范围，其中平面应力分析，Ale则取值为1/2单元边界线长度[7]。

1.3 黏弹性边界单元参数

将黏弹性人工边界等效模拟成为连续分布的并偶联的弹簧-阻尼器系统，如图3所示。其中，平面分析中黏弹性人工边界等效的弹簧特性为KB和阻尼系数CB分别为：

式中：KBT、KBN分别为法向与切向弹簧刚度；R为波源至人工边界点的距离；CBT、CBN分别为垂直向与剪切向阻尼器的阻尼系数；CP、CS分别为介质的P波和S波波速；G为介质剪切模量；αN和αT分别为平面垂直向及剪切向黏弹性边界修正系数；αT值范围为[0.35，0.65]，αN的取值范围为[0.80，1.20]，在本文中αN取为1.0，αT取为0.5。

1.4 黏弹边界外源输入方法

刘晶波和吕彦东给出一种将人工边界入射场转化为等效边界力从而化外源波动问题为内源波动问题的黏弹性人工边界外源输入方法，并在二维平面问题中得到应用。由黏弹性边界弹簧-阻尼元件和内部计算区有限元模型共同构成整体计算模型，当人工边界入射位移场在模型的人工边界入射时，可以通过施加一个等效外荷载来代替人工边界入射位移场。在边界节点垂直向和剪切向上土体震动位移所需施加的等效地震力可分为有限域介质抵抗力及边界弹簧-阻尼元件的反力。工程中，地震源距离场地比较远，一般把地震波假设为地表竖直自由向上入射的平面体波，例如垂直向上的平面SV波。入射场就是人工边界入射场，侧边界无入射。质点只有水平方向上的运动[8-10]。

2 数值分析

场地简化计算模型见图3，并设4个观测点。在模型底部垂直入射SV波，入射波位移方程式（5）和式（6）。通过提取左边界上表面节点A和下表面的节点B的X向位移信息以及中间处上表面节点D和下表面的节点C的X向位移的对比情况，来验证黏弹性边界的合理性（见图4~图5）。

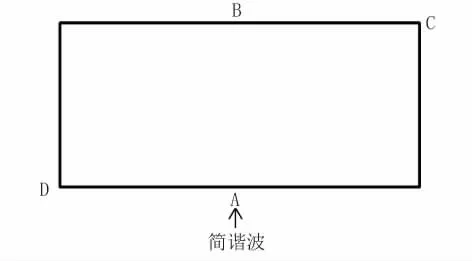
图3 场地简化分析模型

图4 施加边界约束

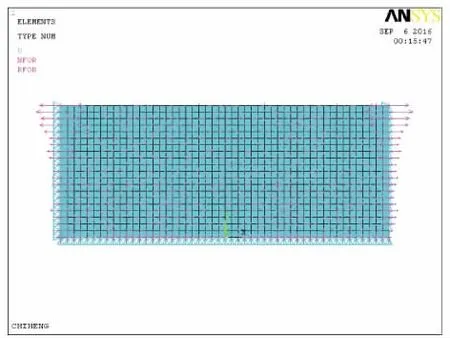
图5 加载求解后的位移图

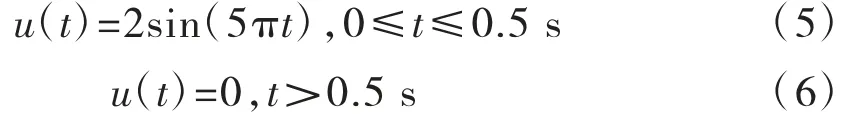
式中：u（t）为正弦位移加载函数，加载时间参数t≥0。介质的弹性模量E=1.85×1010Pa，介质的泊松比μ=0.35，介质密度E=2637kg/m3。计算区域尺寸为：长×宽=1000×400m。

模型中观测点坐标分别为A（0，0）,B（0，400），C（500，400），D（-500，0）。输出D点位移、速度、加速度时程曲线图，如图6、图7；A、B、C、D点位移时程曲线及各点间的对比曲线，如图8~图13。

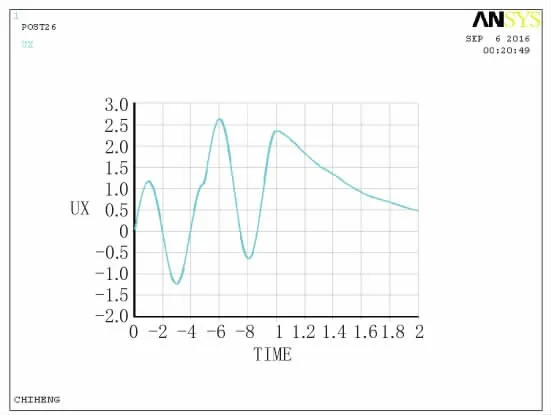
图6 D点位移时程曲线图

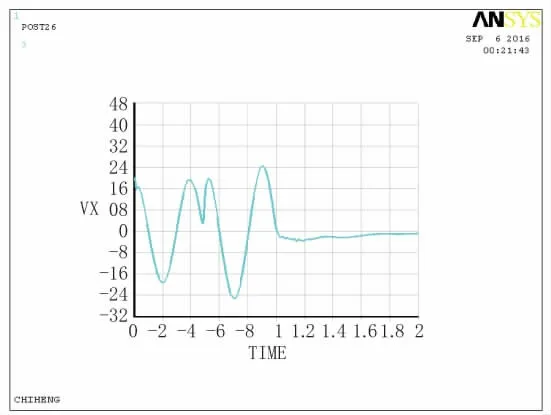
图7 D点速度时程曲线图

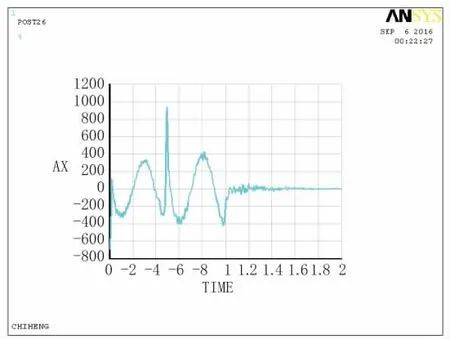
图8 D点加速度时程曲线图

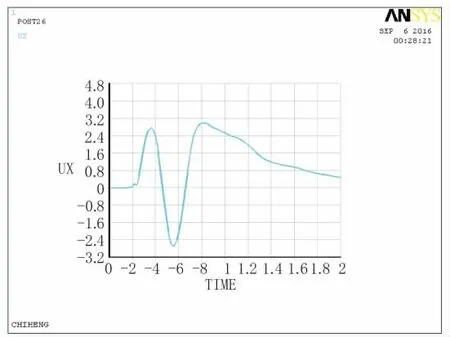
图9 B点位移时程曲线图

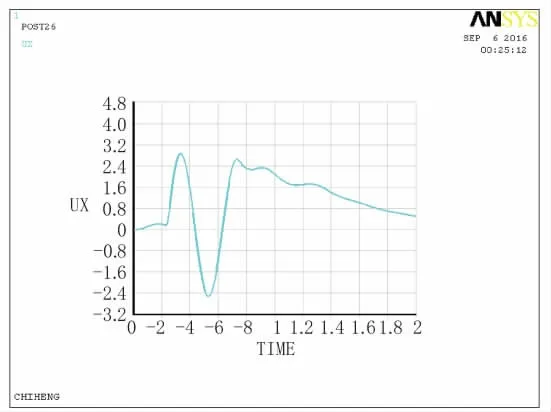
图10 C点位移时程曲线图

图11 A点位移时程曲线图

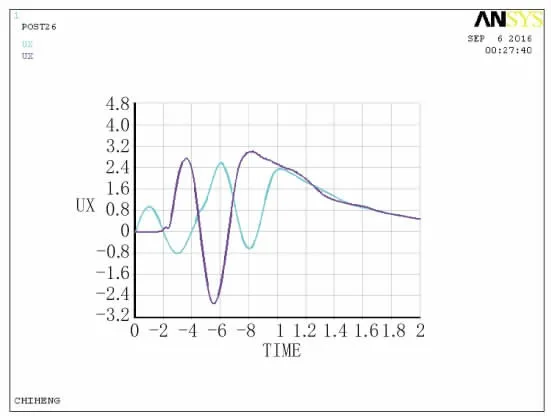
图12 A点、B点位移时程曲线图

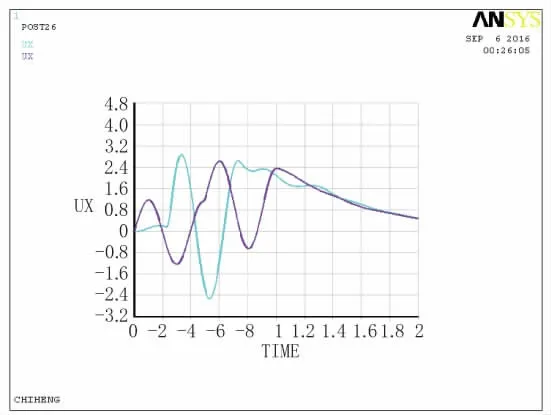
图13 C点、D点位移时程曲线图

通过对比各个观测点的位移时程曲线及单点加速度、速度时程曲线可知，模拟边界有效避免黏性边界产生的低频漂移现象，节点振动和波的传播速度及振幅想对应，并且振动能够模拟场地有限区域之外的半无限介质动力恢复性能，说明土单元随地震波动具有稳定的频率。其中A点有一定的延时，为作用停止后的短暂时间内,会有滞后的位移,接着位移趋向为零。这都与理论解相一致。

其模拟边界方法比其他常用边界更易于在各种通用有限元程序中实现，因此，该边界模型可较为真实的应用于核电厂、地下综合体结构等重大工程的抗震安全分析及隔振工程数值分析。

3 ANSYS施加黏弹性边界命令

4 结 语

本文对黏弹性人工边界基本理论与等效荷载波动输入方法进行了总结，并依据实际工程案例，实现ANSYS有限元自由场振动分析与实际工程中的应用。且通过计算表明黏弹性人工边界具有满意的计算精度和稳定性，可广泛应用于地下工程抗震分析中。