基于灰色预测模型的农村电子商务发展规模预测

李闪闪,刘解放

（天津职业技术师范大学经济与管理学院,天津 300222）

目前,我国农村电子商务发展取得了一定的成绩,值得一提的是在打赢脱贫攻坚最后一公里的路上,农村电商扶贫起到了中流砥柱的作用.随着“互联网+”及数字乡村的深入发展,农村网民规模持续增长,国家各种政策大力扶持,电子商务农村化也将会越来越普及,实现乡村振兴的战略目标指日可待.准确预测未来农村电子商务发展趋势,对我国数字经济建设至关重要.

国内外的相关学者针对农村电子商务各方面展开了深入研究.国内一些学者主要从以下几个角度展开研究,关于农村电子商务发展模式研究:刘亚军等[1]根据全国第一批20 个“淘宝村”的数据,分析了对“互联网+农户+公司”模式的分类、性质和成功因素并给出了相关建议;聂园英等[2]以构建农产品电商服务体系为出发点,初步形成了两个农村电子商务发展模式,即“生产者+网商+互联网”和“生产者+村级服务站+县级运营中心+互联网”.关于农村电子商务发展过程中相关影响因素的研究:张勤等[3]通过因子分析方法,对我国31 个省市的指标数据进行整理分析,得出相关结论并给予相应建议;覃棹[4]通过对我国农村电子商务发展现状进行分,指出发展制约因素,并给予了相关建议.关于农村电子商务发展中出现的问题及应对策略研究;谢天成等[5]提出农村电子商务发展中的显而易见的问题,例如无序性、规模小等,并结合发挥五大发展理念的引领作用,给予了相关建议;任晓聪等[6]对我国电子农村电子商务发展中的电商人才短缺、网络体系建设不健全、农村电子商务监管不力等问题进行研究并给予了相关建议[6].其他学者对农村电子商务的研究也取得了一些成果[7-10].

综合以上学者的研究成果不难发现,大多学者研究集中在农村电子商务的对策建议、影响因素、发展模式方面上,而对农村电子商务发展规模的预测关注较少.基于此,本文以2014—2019 年农村电子商务网络零售额为原始数据,构建了GM（1,1）、DGM（1,1）以及NDGM（1,1）模型,对我国农村电子商务发展规模进行预测和精度比较,结果表明NDGM（1,1）模型预测精度更高,更适合用于对我国农村电子商务发展规模预测研究.

1 灰色系统理论

灰色系统理论是由我国著名学者邓聚龙教授所创立,是一种研究少数据、贫信息不确定性问题的新方法.现实世界中,“小样本”“贫信息”不确定性系统的普遍存在决定了灰色系统理论具有十分广泛的应用领域.目前,灰色系统已经广泛应用于工农业生产、工程、科技、军事等许多领域,国内外一些学者也对灰色系统进行了深入的研究,并取得了一些成果[11-21].灰色系统预测是通过对原始数据进行处理和分析,之后构建灰色模型,对未来的状态进行定量预测.由于我国农村电子商务起步较晚,数据相对较少,而这正好符合灰色系统中的“小样本”特征,故可利用灰色系统理论中的相关模型进行预测.

1.1 原始数据处理

在进行GM（1,1）建模之前,需要对原始序列数据进行检查,检验数据是否符合建模要求,判断依据为级比检验.

若出现不符合上述要求,则需要对原始序列数据进行处理,引入相应的序列算子.常用的序列算子有平均弱化缓冲算子、加权平均弱化缓冲算子、加权几何平均弱化缓冲算子、均值强化缓冲算子、平均强化缓冲算子等.本论文中会引入二阶弱化算子来处理历史数据,步骤如下:

设原始序列为

引入二阶弱化算子D2,令

再令

1.2 GM（1,1）建模过程

在GM系列模型中,邓聚龙教授所提出的均值GM（1,1）模型应用最为广泛,G 代表grey（灰色）,M代表model（模型）,GM（1,1）代表1 阶的1 个变量的模型.

GM（1,1）建模过程如下:

原始序列为

对X(0)进 行一次累加,生成（1-AGO）序列X(1)

根据X(1)序 列求出其紧邻均值生成序列Z(1)

GM（1,1）的基本形式为

式（5）中:a为发展系数,b为灰色作用量.

建立GM（1,1）模型均值形式x(0)(k)+az(1)(k )=b的白化微分方程,即

当t=1 时,令x(1)(1)=x(0)(1),代入式（3）中,求得

将式（8）代入式（7）中,可得GM（1,1）模型的时间响应式为

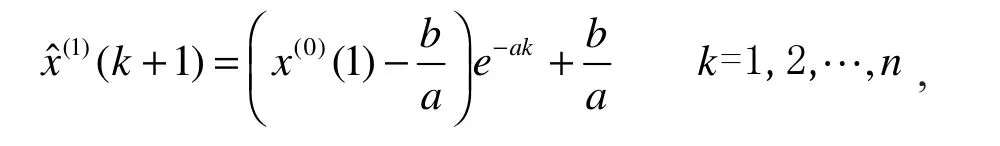
其累减还原式为

1.3 DGM（1,1）建模过程

在应用GM（1,1）模型建模时存在一些问题,因为GM（1,1）模型的构建过程中将离散方程求得的参数代入到连续方程这出现了从离散形式到连续形式的跳跃,而刘思峰等人提出的DGM（1,1）模型可以解决这个问题.

DGM（1,1）建模过程如下:

设非负序列

其一次累加序列为X(1),即

DGM（1,1）模型为

由此可以求出β1和β2的值.

式（10）的通解为

当k= 0时,取x(1)(0) =x(0)(1),代入式（11）中,可以求得

再将式（12）代回式（11）,可得DGM（1,1）模型的时间响应式为

其累减还原式为

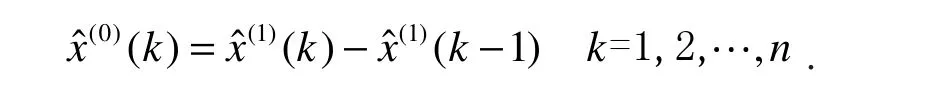
1.4 NDGM（1,1）建模过程

虽然DGM（1,1）模型解决了GM（1,1）模型从离散形式到连续形式的跳跃,但是这两个模型的适用范围是近似齐次指数序列,对于近似非齐次指数的序列需要用NDGM（1,1）模型来预测.

NDGM（1,1）建模过程如下:

设原始序列

式（13）中:x(0)(k) ≥ 0,k=1,2,…,n.

X(1)为其一次累加序列（1-AGO）,即

NDGM（1,1）模型为

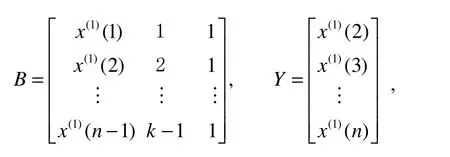
由此可以求出β1,β2,β3的值.

可得NDGM（1,1）模型的递推表达式为

还原预测值为

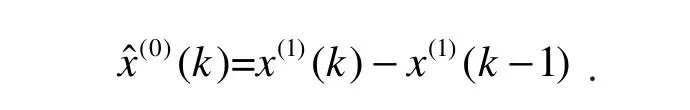
1.5 精度检验

目前灰色系统预测包含了很多模型,但是到底哪种模型预测相对更为精确,需要进一步检验模型的精度.本文采用的是相对误差检验法.

1.5.1 残差及相对误差检验 设有原始序列

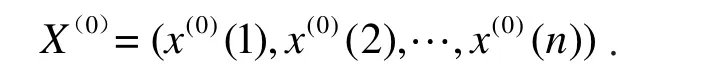
其相应的预测模型模拟序列

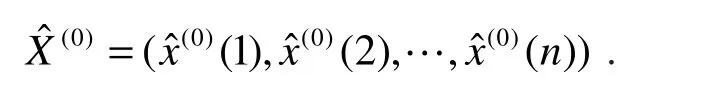
则有残差序列

相对误差序列

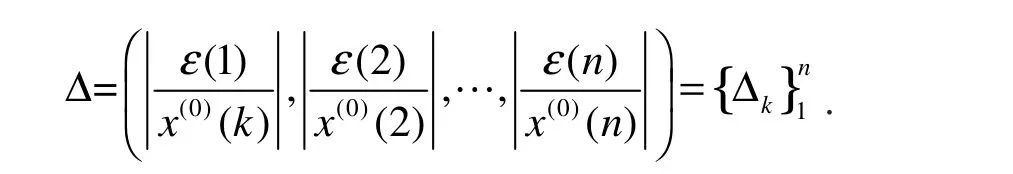
k点相对误差

平均相对误差（MAPE）

1.5.2 关联度检验 设有原始序列X(0), 其相应的模拟序列为,则两者的绝对关联度

1.5.3 均方差比与小概率误差检验 设有原始序列X(0), 其相应的模拟序列为,残差序列为ε(0),则可得

原始序列X(0)的均值、方差分别为

残差序列ε(0)的均值、方差分别为

均方差比值为

小误差概率为

常用的精度等级如表1 所示内容.

表1 精度检验等级参照表Tab. 1 Reference table for accuracy test levels

2 农村电子商务发展规模分析

2.1 数据来源与处理

2.1.1 数据来源 本文数据来源于商务大数据, 选取2014—2019 年中国农村网络零售额为建模历史数据,如表2 所示,以此进行GM（1,1）、DGM（1,1）、NDGM（1,1）模型建模并进行精度检验.

表2 2014—2019 年中国农村网络零售额Tab.2 Online retail sales in rural China from 2014 to 2019

2.1.2 数据处理 进行建模之前,首先检测下原始序列中的数据是否符合建模,若不符合需要引入序列算子进行调整后建模.

原始序列

级比序列

可知,n=6,σ(k) ∉=(0.7513,1.3307).

分析原始序列数据,可知数据增长速度过快,通过级比检验发现只有一部分级比落在了要求之内,故需要对数据做进一步处理.考虑到当时对农村电子商务发展比较有利的政策因素,引入二阶弱化算子来弱化快速增长趋势.

原始序列为

引入二阶弱化算子D2,令

式（17）中:

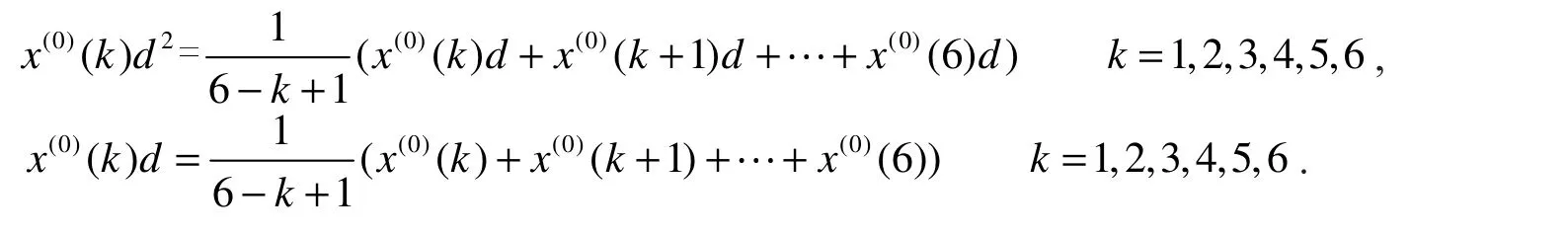
可得

经计算该序列通过级比检验符合要求,所以在进行后续GM（1,1）、DGM（1,1）和NDGM（1,1）建模时,可以使用处理后的序列,即X(0)=(13437.50,14208.79,14976.67,15622.52,16231.95,17082.80)进行建模和预测.

2.2 GM（1,1）、DGM（1,1）和NDGM（1,1）建模过程

2.2.1 GM（1,1）建模运算过程 GM（1,1）模型出现较早,应用已经很成熟,因而建模过程可参考前面的理论部分,此处略去建模的详细过程,经过计算可得:

GM（1,1）模型的时间响应式为

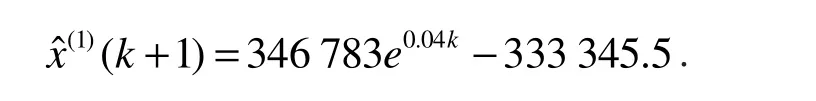
其累减还原式为

于是可得模拟序列为

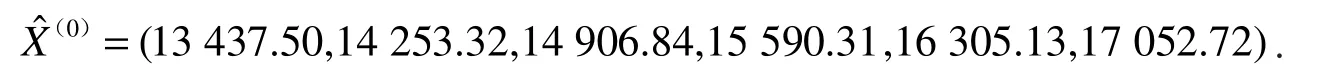
2.2.2 DGM（1,1）建模运算过程 原始序列为

其1-AGO 序列为

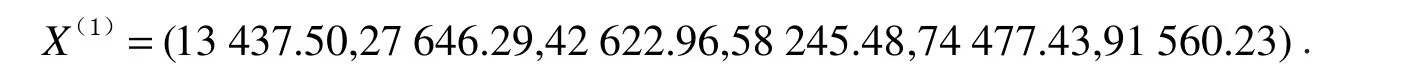
DGM（1,1）的离散形式为

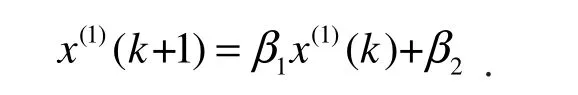
经计算可得β1= 1.05,β2=13639.68.

由此可求出模拟序列为

2.2.3 NDGM（1,1）建模运算过程 原始序列为

其1-AGO 序列为

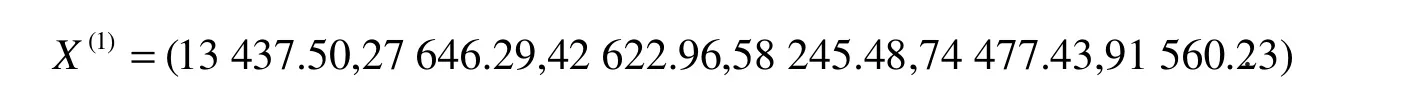
NDGM（1,1）的公式为

经计算可得β1=1.0241,β2=333.1226,β3=13584.1110.

根绝模拟递推公式,可得模拟序列为

2.3 精度检验与分析

利用灰色系统建模软件7.0.1 及MATLAB 软件编程计算各模型的模拟值、残差、相对误差,计算结果如表3 所示.

表3 GM（1,1）、DGM（1,1）和NDGM（1,1）模型精度检验Tab.3 GM（1,1）,DGM（1,1）and NDGM（1,1）model accuracy tests

通过表3 可知,GM（1,1）、DGM（1,1）和NDGM（1,1）模型的平均相对误差分别为0.32%、0.32%和0.25%,再结合图1 的拟合效果图,可以得出以下结论:NDGM 模型拟合精度较高,更适合用于农村电子商务发展规模的预测,因而可用该模型预测2020—2025 年农村电子商务发展趋势.

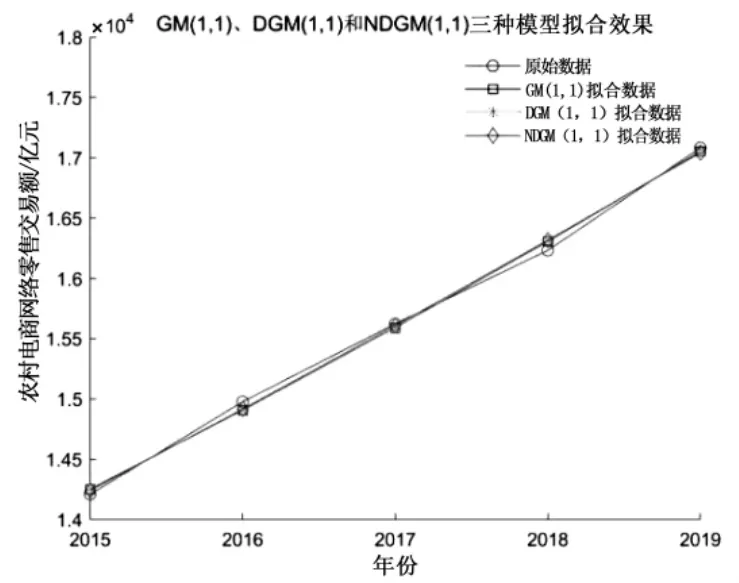
图1 GM（1,1）、DGM（1,1）和NDGM（1,1）模型拟合效果Fig.1 GM（1,1）,DGM（1,1）and NDGM（1,1）model fitting effects

3 农村电子商务发展规模预测

3.1 发展规模预测

因为农村电子商务网络零售额的最初原始数据增长较快,考虑到当时政策因素影响,所以要使用处理过后的数据,作为预测的初始数据.通过之前三种模型对比分析,已经得出NDGM（1,1）模型模拟精度较高,所以在这里选择使用NDGM（1,1）模型来预测未来农村电子商务发展趋势,通过MATLAB 程序计算可算出2020—2025 年农村电子商务零售额如表4 所示.分析数据可知未来农村电子商务发展趋于平稳上升态势,这与我国由高速发展向高质量发展的规划目标不谋而合,这更有力地说明农村电子商务发展工作重心要放在高质量发展上.

表4 2020—2025 年农村电子商务网络零售额Tab.4 Rural e-commerce online retail sales from 2020 to 2025

3.2 对策建议

综合以上分析,要使农村电子商务发展由高速发展向高质量发展应注意以下几点.

3.2.1 农村电商监管政策 现在由于电商入驻门槛较低,很多人一味追求利润最大化,很多不符合规格的产品在电商平台进行了交易,忽略了产品质量,此外还有行业中的恶意竞争现象,严重破坏了农村电子商务市场规则.这需要有相关部门加强监督管理,出台相关政策来约束.

3.2.2 培养专业电商人才 现在农村经营电商平台的人越来越多,可真正懂运营的专业人才短缺,导致很多人虽然开了网上店铺,但由于缺少专业的技能,导致店铺整体运营效果不佳,最后不得不关店.倘若这些人经过专业的培训或者有专业的电商运营人才给予指导,将会使经营者少走弯路,也会带动更多的农村创业者转到电商行业创业.

3.2.3 加快构建物流体系 很多农村住户分散,村庄之间距离较远,快递成本比较高,物流体系不完善,农村电子商务也因为快递“最后一公里”问题而发展缓慢,所以解决快递问题迫在眉睫.政府相关部门应结合不同区域农村现状,提供不同的方案,尽早去解决.

4 小结

本文以农村电子商务发展为出发点,以2014—2019 年历史数据为建模初始数据,通过构建GM（1,1）、DGM（1,1）和NDGM（1,1）三种灰色模型,得出各模型的计算精度,然后进行对比分析,确定NDGM（1,1）模型的拟合数据更为精确,更适合用来做农村电子商务的预测;随后使用NDGM（1,1）模型预测了农村电子商务2020-2025 年发展规模,最后给出了一些相关建议.本文的相关结论可以为有关部门制定农村电子商务相关决策提供依据,为我国农村电子商务进一步研究打下基础.