混合关键级任务资源需求的概率性分析
张 通,郑 浩,朱长昊,张凤登
(上海理工大学光电信息与计算机工程学院,上海 200093)
0 引言
混合关键级系统[1-4](Mixed-Criticality Systems,MCS)在运行资源宽裕的条件下,系统不再单纯为保证安全关键性任务(高关键级任务)运行,而是尽力保证非安全关键性任务(低关键级任务)的服务质量。任务在MCS 中运行一般通过执行预算[5-6](Execution Budgets)控制,所有任务运行时都不会超过预算。任务执行预算通常根据任务的最坏情况执行时间(Worst Case Execution Time,WCET)进行安排,这导致低关键级任务不必要地被赋予了一定的安全关键性。本文将概率性最坏情况执行时间[7-8](probabilistic Worst Case Execution Time,pWCET)引入传统的MCS 模型,通过概率性实时分析方法研究系统的可调度性[9]。概率性实时分析中将任务资源调度失败视为系统失效,高关键级任务错过截止期概率可设定在某个极其低的水平(如10-9/h);低关键级任务则允许更高的水平(如10-6/h)。现实中安全关键性系统也存在随机性行为,如在先进硬件架构多级缓存中的数据随机替换策略或倒车泊车雷达中的随机频率声波[10]。
本文提出了概率性需求边界函数模型(probabilistic Demand Bound Function,pDBF),通过分析系统整体的资源需求过载概率来进行可调度性分析。考虑任务执行预算与pWCET 的联系,说明在MCS 的不同模式下如何得到pDBF,丰富了MCS 模型;设计了针对混合关键级零星任务集的可调度性测试算法,分析了算法复杂度以及系统其他参数对可调度性的影响。
1 相关工作
文献[11]提出了概率性时间需求分析方法(Probabilistic Time Demand Analysis,PTDA),针对弱实时或混合实时系统进行研究;文献[12]开创性地针对WCET 采用概率性分析方法,以避免系统资源过度预置;以概率性最坏情况响应时间分析为代表,文献[13-15]针对固定任务优先级调度策略下的周期性任务系统采用不同于pWCET 的设定,这里假设任务所有可能执行时间的概率分布已知。在考虑任务间概率性抢占下,计算概率性最坏情况响应时间。相关文献中任务模型拓展至包含pWCET 与pMIT。另外就是一类以实时接口(real-time interface)分析模型为基础的研究,文献[16]基于此提出了概率性实时演算框架(probabilistic real-time calculus),同时考虑了pWCET 与pMIT,并同样基于需求边界函数提出了针对EDF 调度的可调度性充分条件,但该框架仅仅从pWCET 或pMIT 的最极端部分分析出发,从而得到的是可调度性的下界。本文主要关注任务最坏情况执行时间,用pWCET 表示,采用类似已有文献的计算原理。
除了围绕pWCET 分析外,还涉及任务概率性最小到达间隔或概率性截止期[17];文献[18]将一段时间内任务到达次数用随机变量表示,缺点是系统模型信息不如其他模型参数丰富。pWCET 的获取可以使用静态概率性时间分析(Static Probabilistic Timing Analysis,SPTA)方法。上述研究假设任务与任务之间的概率性参数独立;pWCET 一般以整数值的离散分布形式给出,本文同样遵循该设定。
针对固定任务优先级调度的MCS,文献[19]采用了类似文献方法,通过计算每个超周期(hyperperiod)内所有任务的错过截止期概率得到可调度的分析结果;此外文献[20]改进混合关键级系统中SMC 与AMC 策略,计算所有模式下任务的错过截止期概率;针对EDF 调度,文献[21]根据pWCET 设定了预算超出概率,改善了系统的可调度性;部分研究将概率性实时分析引入能耗约束的MCS 调度设计中,文献[22]提出了基于测量估计的概率性分析来估计任务最坏情况下的能量消耗(Worst-Case Energy Consumption,WCEC),但没有结合具体的能耗资源管理算法;Bhuiyan 等[23]基于概率性方法提出了能耗影响的速率控制,并结合动态电压频率调节技术(Dynamic Voltage and Frequency Scaling,DVFS)实现了系统能耗最小化;关于多核处理器平台MCS,文献[24]基于概率性的DAG 分析量化MCS 中低关键级任务;Zeng 等[25]在同构多核处理器平台上,提出了概率性混合关键级任务模型,得到相应的任务分区算法PPDC,使低关键级任务运行得到提升。本文提出的概率性需求边界函数模型,可计算任务系统在调度周期内的资源需求过载概率,在避免资源过度预置的同时改善系统可调度性。
2 符号与模型定义
2.1 符号定义与概念
pWCET 为整数取值的离散型随机变量,可用概率质量函数(Probability Mass Function,PMF)表示,即f(ici)=P(Ci=ci)=pi,i=0,1,…,k,或记为:
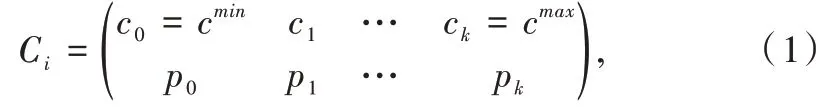
规范假设c0<c1<…<ck,Ci的范围为[cmin,cmax]。pi须满足pi≥0,i=1,2,…,k,且Σk i=1pi=1。概率分布函数(Cumulative Distribution Function,CDF)表示随机变量小于某个值的概率和,即F(ix)=Σx y=xminf(iy),x∈[cmin,∞)。两个相互独立随机变量X 与Y 的卷积和定义为P(Z=z)=Σ∞k=-∞P(X=k)P(Y=z-k),记为Z=X⊗Y;相应卷积差记为Z=X⊖Y=X⊗(-Y);若干部分概率和为1 的随机变量分布的合并称为联合,记为Z=X⊕Y。
随机变量X1和X2间的比较,若对任意x 两个随机变量的CDF 满足FX(1x)≤FX(2x),则称X1大于等于X2,记为X1≽X2,在CDF 曲线上X1始终位于X2下方;反之称X1小于等于X2,记为X1≼X2。约定x 与y 最大值为〚x〛y,x 与y 最小值为〚x〛y。
2.2 任务系统模型
在单处理器硬件平台上,任务系统由一组个数为n 的零星任务集τ={τ1,τ2,…,τn}构成。单个任务τi用(Ti,Di,Ci,Li)元组定义,分别表示任务周期、概率性最坏情况执行时间、相对截止期以及任务关键级。系统实际运行是通过设置执行预算的方式,所有任务在低关键级模式下执行预算为Bi。本文限制为双关键级系统,即Li={LO,HI}。任务τi的 第j个 作 业 记 为Ji,j。任 务Di≤Ti,cmax≤Di。任 务 与 任务之间不存在顺序或互斥关系;任务不同作业之间相互独立。
定义低关键级任务子集τL={τi∈τ|Li=LO},高关键级任务子集τH={τi∈τ|Li=HI}。定义任务τi的平均利用率与系统τ的平均利用率为:

系统从低关键级模式开始运行,当任务作业实际执行时间未超过执行预算Bi时,系统处于低关键级模式;当高关键级作业执行超过其Bi时,提升系统关键级模式。上述系统模式切换是基于内部触发的机制,还有一种外部触发机制[26],后者认为外部事件也能导致系统被动地提升关键级。模式切换后所有低关键级任务作业会被抛弃,并且在高关键级模式下不会释放;系统运行在高关键级模式时,若出现调度空闲,则系统关键级回落。
3 概率性需求边界函数
3.1 概率性需求边界函数定义
对于零星或周期任务,任意时间范围Δ内,任务τi的需求边界函数[27](Demand Bound Function,DBF)为:

其中,Ci是任务WCET,从而系统τ的需求边界函数为:

对于固定速率单处理器,任意时间范围Δ内系统提供资源可用供给边界函数[28](Supply Bound Function,SBF)来描述,即:

定理1:若任务系统τ在任意时间范围Δ内的需求边界函数总是不大于系统的供给边界函数,则在EDF 算法调度下任务系统τ是可调度的,即满足:
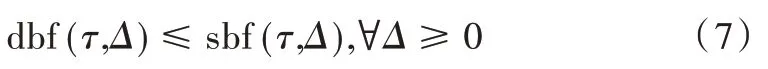
定义1:若任务的最坏情况执行时间使用pWCET 描述,则任意时间范围Δ内,该任务的需求边界函数簇可以用概率性需求边界函数(pDBF)描述如下:


通过例1 说明pDBF 暂时不设任务关键级。将DBF 分析中使用的WCET 设为表1 中黑色方框内数值,此时系统利用率大于1,在EDF 算法下不可调度[29]。

Table 1 Model task set of example 1-pDBF表1 例1pDBF 模型任务集
以Δ=10 为例,按式(1)和式(2),任务系统DBF 为11,任务系统不可调度;同样对于Δ = 10,各个任务的pDBF 分别为:

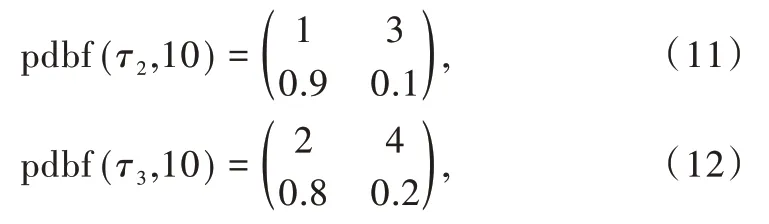
整个任务系统的pDBF 为:

图1 表示一个超周期内任务系统的DBF 和pDBF。任务系统pDBF 所有可能值如图中灰度部分所示,对应概率越大则灰度越深。随着时间范围的增大,出现极端资源需求情况的概率越来越小。pDBF 模型仍然包含了DBF 模型中所有信息,任务系统在Δ=10 时发生资源需求过载的概率(Demand Overload Probability,DOP)为0.000 2,如果允许任务系统以不大于某个概率阈值HT发生资源需求过载,如0.001,那么例1 的可调度性将放宽。

Fig.1 The pDBF of the example task set and the compared DBF图1 示例任务集的pDBF 和与其相比较的DBF
3.2 可调度性分析
先给出几个相关定义。某个任务τi=(Ti,Di,Ci)的第j次作业记为Ji,j=(ti,j,ri,j),ti,j表示作业释放时刻,ri,j表示作业响应完成时刻,如果Ji,j完成时刻大于其绝对截止期时刻,即ri,j>ti,j+Di,则所有可能的ri,j对应的概率之和称为Ji,j错过截止期概率(Deadline Miss Probability,DMP),即DMPi,j=P(Ri,j>ti,j+Di),Ri,j表示作业Ji,j所有可能最坏响应完成时刻所构成的随机变量。
定义2:对任意时间范围Δ,若任务系统τ的需求边界函数大于供给边界函数,则称任务系统发生需求过载;任务系统pDBF 大于SBF 这部分概率和的最大值,称τ为在Δ内的需求过载概率,记为DOPτ,Δ,即:

下面证明一个引理,将DOPτ,Δ与任务作业的DMPi,j联系起来。
引理1若任务系统τ在任意时间范围Δ内的需求过载概率DOPτ,Δ不大于某个概率阈值HT,则在该时间范围Δ内所有任务作业错过截止期概率也一定不大于HT,即满足:

其中任务作业须满足ti,j+Di≤Δ。
证明:首先考虑Δ≥max{D1,D2,…,Dn}=Dmax的情况。设τ在Δ内的DOPτ,Δ≤HT但大于0,根据定理1,任务作业错过截止期的可能性是必然存在的。将系统报告出现调度失效的最早时刻记为tf∈(Dmax,Δ],则HT≤DOPτ,tf≤DOPτ,Δ。在tf时刻之前根据EDF 调度策略,以tf为绝对截止期的任务作业将在所有之前已释放作业中被调度。设这部分作业为Jri,j=tf={J1,J2,…,Jm}(来自不同任务省去作业序号下标),此时错过截止期的作业全部或至少一个来自Jri,j=tf。以tf之前时刻为绝对截止期的任务作业,自然在tf之前就完成调度或者报告调度失败,这里分两种情况讨论:
情况1:只有作业J1在tf时刻可能错过截止期,J1错过截止期的概率为DMP1,显然DOPτ,tf=DMP1。
情况2:可能错过截止期的作业有k(≤m)个,错过截止期概率分别为DMP1,DMP2,…,DMPk。由于作业绝对截止期都相同,所以任务ID 最小的作业尽管已经被优先调度,但仍可能以DMP1概率错过截止期,其他优先级更低的任务将肯定得不到调度而错过截止期,所以有DMP1≤DMP2≤…≤DMPk。任何无法完成调度的作业最后都会造成DOP不为0,所以DOPτ,tf=max{DMP1,DMP2,…,DMPk}=DMPk。
Δ<max{D1,D2,…,Dn}相当于缩小任务集范围,上述分析同样适用。综上所述,HT≥DOPτ,Δ≥DOPτ,tf≥DMPi,j,∀Δ≥0,∀τi∈τ。
将例1 中任务截止期进一步设值为D1=3,D2=7,D3=7。图2 考虑Δ=8 这一情况,t7时刻就是该情况下的tf,此时任务Jri,j=tf={J1,J2},分别属于τ2与τ3。此时DMP2=0,DMP3=0.02,DOPτ,Δ=0.0226。

Fig.2 An example of the relationship between system DOP and task DMP图2 系统DOP 与任务作业DMP 的关系说明示例
综上,DOP 比基于DMP 的分析更加可靠,由此得出可调度性结论:若在任意时间范围Δ内,任务系统τ的概率性需求边界函数pDBF 可以在其DOP 不大于某一阈值HT的条件下满足Δ内的资源供给,则认为系统是可调度的。
4 混合关键级任务的概率性需求边界函数
MCS 的任务调度常采用EDF-VD[30]的调度策略。利用缩短后的虚拟截止期DLO i 来弱化模式切换给系统DBF带来的影响。对于τi∈τH,有DLO i≤Di,DLO i≽Ci。首先提出MCS 的可调度性命题:
命题1:对于一个使用pWCET 参数的混合关键级系统任务集τ,在EDF 算法调度下,若系统在高关键级模式以及低关键级模式下,其资源需求过载概率都不大于给定的可调度性概率阈值HT,则认为任务系统是可调度的,即:

证明:若任务被允许以极其微小概率HT错过其截止期,则等同于系统运行平均失效时间必须大于设计者给定的系统运行预期寿命。为保证高关键级任务在所有模式下都有相同程度的可靠性保证,HT的所有模式是统一的。基于这样的系统可靠性保证,结合引理1,原命题为真。
4.1 根据任务执行预算重构任务的pWCET
图3 为重构任务的pWCET 概率分布,在低关键级模式下pDBF 中使用C LO i,在高关键级模式下仍使用完整的Ci,这体现预算Bi对系统的控制作用。对于τi∈τL,一但运行超过Bi就会被调度器中止,所以重构将超出Bi部分的概率堆叠到Bi处;对于τi∈τH,运行超过Bi会使系统提升关键级,但这部分需求考虑在高关键级模式分析中,所以重构将这部分概率堆叠到0。任务Bi的设置存在天然矛盾性:Bi设置过小,低关键级任务运行的服务质量将恶化,高关键级任务更易预算超支;Bi设置过大将损害低关键级模式的可调度性。

Fig.3 Reconstructing C LO i based on task pWCET for pDBF computation of task system图3 根据任务的pWCET 重构C LO i 以用于任务系统的pDBF 计算
4.2 结转作业资源需求分析
任何高关键级任务在系统发生模式切换时,都可能存在结转任务J⊢i,可将J⊢i视为在模式切换时释放的新作业。
在保证高关键级作业在可调度条件下,必须进行最坏情况分析。假设J⊢i 会被尽可能迟地释放,即J⊢i 在原来低关键级模式下调度时恰好在截止期前完成,但J⊢i 在系统切换为高关键级模式后其执行时间大于Bi的概率一定大于0,即τi超过执行预算Bi的概率。
如图4 所示,J⊢i 可能包含的情况有3 部分:①作业在模式切换前可能已经执行;②在剩余调度窗口l⊢i 内为原低关键级模式下剩余的执行需求;③由于模式切换而导致突然增加的执行需求(这种情况一定存在)。下面将例1 中任务τ2拓展为例2(见表2),并分析J⊢i 的执行需求C⊢2。

Fig.4 Worst case scenario of carry-over job图4 结转作业可能出现的最坏情况

Table 2 Model task τ2 of example 2-pDBF表2 例2-pDBF 模型任务τ2
J⊢2在未发生模式切换时,其截止期前至多满足B2个单位的资源需求。l⊢2 满足0≤l⊢2<Di=8,以l⊢2=2 为例,对C2各个部分分别分析。对于c1=1<l⊢2,从最坏情况考虑,把它归类到如图4 所示的第②部分,得到C ,⊢,head2;对于l⊢2<c2=3≤B2,由于在剩余执行窗口内至多执行l⊢2 个单位,则至少有1 个单位已经被执行了,即包含了图4 中的①、②部分,得到C ,⊢,mid2;对于l⊢2<B2<c3=5,由于至多保证B2个单位执行需求被满足,所以有c3-B2= 2 个单位无法得到满足,包含在第①、②、③部分中。得到C,⊢,tail2如下:

但无论l⊢2 多长,肯定包含第③部分,这导致无法满足HT的约束,而EDF-VD 调度算法可缓解这一问题。
为了给第③部分执行预留空间,采用EDF-VD 调度算法为每个高关键级任务设置虚拟截止期DLO (iCi≼DLO i≤D)i。如图5所示,使用虚拟截止期后J⊢i获得更长调度窗口。
引理2(结转作业的执行需求):对于高关键级任务τi∈τH的作业,其在低关键级模式以及高关键级模式下的EDF调度分别根据DLO i 与Di进行。若在低关键级模式下,系统的资源需求可以得到满足,则模式切换后其结转作业J⊢i 的剩余调度窗口长度为l⊢i≥0,则有:
(1)若l⊢i<Di-DLO i,表示该作业在模式切换前已经完成,不用进行作业结转。
(2)若l⊢i≥Di-DLO i,表示该作业必然为一个结转作业,即在模式切换后该作业仍有执行需求C⊢i,且C⊢i 如式(19)、式(20)所示,其中l⊢’i=l⊢i-(Di-DLO i)。
证明:对于l⊢i<Di-DLO i,表示模式切换发生在虚拟截止期DLO i 之后,所以作业在模式切换前已完成,不用作业结转;对于l⊢i≥Di-DLO i,当0≤l⊢i′<Bi时,由于l⊢i′不足以完成Bi个执行需求,所以必然有部分需求已执行,C⊢i 须扣除这部分,所以C⊢i 包含①、②、③部分;对于Bi≤l⊢i′<DLO i,须把整个执行预算内的需求放在l⊢i′内考虑,不包含第①部分,C⊢i 包含第②、第③部分。如图5 所示。
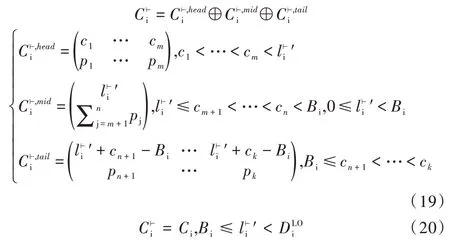

Fig.5 By using virtual deadline to left more scheduling windows for J ⊢2图5 通过使用虚拟截止期为J⊢2 空出更多的调度窗口
4.3 不同模式下系统的pDBF
在低关键级模式下,系统成为标准的零星任务系统,其低关键级模式下任务系统的pDBF 为:

l⊢i 越长表示越可能存在结转作业。如图6 所示,为了更多地考虑任务作业,可将完整的任务作业在Δ内尽可能往后排,以空出尽可能大的l⊢i,长度为Δ modTi。当l⊢i<Di-DLO i 时,J⊢i 不存在;Bi+(Di-DLO i)≤l⊢i<Di时,l⊢i 可以容纳一个完整作业,J⊢i 等同一个正常作业;Di-DLO i≤l⊢i<Bi+(Di-DLO i)时,须考虑有一个结转作业情况。综上,高关键级模式下pDBF 可表示为:

其中


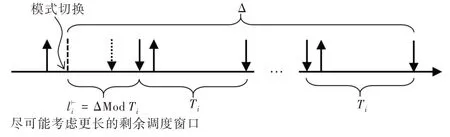
Fig.6 The worst case distribution of high critical job图6 高关键级任务作业的最坏排布情况
5 实验结果与分析
5.1 生成实验任务集
随机实验任务集生成参数设置如下:①任务关键级Li:CP 表示生成任务为高关键级任务的概率,默认为CP = 0.5;任务周期Ti设置为25·ω,汽车或航空器中常见的实时任务周期一般为20~1 000ms,所以ω随机选择[1,40]范围的整数;②任务平均利用率Uavgτi基于UUnifast 算法[31]生成;③任 务Ci:根据=Ti·Uavgτi以及随机生成的WCET参数cmaxi∈[1.1i,2Cˉ]i,按内推插值法生成序列(c0,c1,…,cmax);Ci没有具体分布,唯一的限制是在分布上呈递减趋势,这里按指数型衰减生成;④任务执行预算Bi:根据任务执行概率阈值PT选择,即满足P(Ci≥Bi)=PT,PT默认为10-5;⑤任务截止期Di、虚拟截止期DLO i:Di=Ti;DLO i 在[Bi,Ti]内随机选取。
5.2 算法复杂度实验
为尽可能彻底测试所提出的可调度性测试算法的时间复杂度,将任务集的任务个数在2~15 范围内变化,任务pWCET 长度在2~15 范围内变化。任务集平均利用率Uavgτ 从0.05~1.05 随机产生;可调度性概率阈值HT在实验开始时从[10-6,10-5]中随机选择,实验结果如图7 所示。z轴表示算法测试所用时间,空间中每个实验数据点取100个随机任务集平均测试时间;算法运行时间与任务集个数以及pWCET 参数长度呈指数关系,任务集个数对运行时间影响更突出,这是因为测试算法的外循环次数为HP+1,内循环次数为任务集中任务个数,基本运算操作为对随机变量的卷积和,所以前者影响更大。综上所述,当测试任务集平均利用率大于1 时,算法运行在线性时间复杂度上,其他情况下则运行在伪多项式时间复杂度上。所以应尽量减小超周期,比如通过取幂值方式。
对于临界时刻释放的周期或零星任务系统,尽管采用了pWCET 参数,但在一个超周期内分析同样有效。测试范围至少应为一个超周期,因为在DBF 模型分析下,lmax指DOP>0 的最早时刻,而在pDBF 分析下,指DOP>HT的最早时刻;另外算法是基于系统不同模式下的平均利用率判定,这利用了随机过程中的更新报酬定理[32]。
算法1:可调度性测试算法
输入:MCS 零星任务集τ={τ1,τ2,…,τn},可调度性概率阈值HT,任务系统超周期HP=lcm{T1,T2,…,Tn};
输出:可调度性分析结果(“schedulable or not schedulable”)。

Fig.7 Executing time of schedulability testing algorithm图7 可调度性测试算法运行时间
ULO avg←CalcuTaskUavg(τL);/*LO-模式平均利用率*/
UHI avg←CalcuTaskUavg(τH);/*HI-模式平均利用率*/
ifULO avg>1||UHI avg>1 then return(“not schedulable”);
end if
fort:= 0 ToHPdo
fori:= 1 To ndo
Lr ←tModTi;/*最大剩余调度窗口长度*/
if Lr==DLO i then
pdbfLO τ←pdbfLO τ⊗CLO i;/*LO-模式系统10.pDBF*/
end if
ifLi==HI&&Di-DLO i≤Lr ≤Bi+Di-DLO i then
if Lr==Bi+Di-DLO i then
pdbfHI_full τ←pdbfHI_full τ⊗C i;
else
pdbfHI_⊢τ←pdbfHI_⊢τ⊗C ⊢i;/*结转作业pDBF*/
end if
end if
end for
pdbfHI τ←pdbfHI_full τ⊗pdbfHI_⊢τ;/*HI-模式系统pDBF*/
DOPτ,t←FindMaxDop(pdbfLO τ,pdbfHI τ);
if DOPτ,t>HTthen return(“not schedulable”);
end if
end for
return(“schedulable”);
5.3 仿真实验
所有任务的截止期等于其周期,下面分析pWCET 参数长度、系统可调度性概率阈值HT以及系统高关键级任务概率CP 等系统参数对可调度性性能的影响。任务集包含10个任务,系统平均利用率以0.05 的步长从0.05 变化到1.0,每个实验数据点测试100 个随机任务集。
(1)改变任务pWCET 参数长度。使用重抽样技术[33],在不降低参数可靠性前提下缩减任务的pWCET 参数长度,当长度抽样为1 时使用传统的DBF 方法分析。
如图8 所示,Uavgτ 较小时(0.05~0.55),pWCET 长度对于可调度性没有显著改善。而当利用率增大时,确定性分析(虚线)的可调度性状况迅速恶化,但在不同pWCET 长度下的可调度性仍有较大提升。但是当pWCET 长度大于8后,这种提升就变得十分有限。

Fig.8 Changing the pWCET parameter length of the task(by re-sampling)图8 改变任务的pWCET 参数长度(通过重抽样方法)
(2)改变系统可调度性概率阈值HT。施加越严格的可调度性概率阈值,系统越可靠。
图9 中,HT越宽松,系统的可调度性越好,但是在系统平均利用率特别小(0.05~0.25)或特别大(0.95~1.00)时,这种表现并不突出。

Fig.9 Changing the probability threshold of system schedulability HT图9 改变系统可调度性概率阈值HT
(3)改变系统高关键级任务概率CP。提高系统高关键级任务的比例会增大系统高关键级模式下的pDBF。
从图10 可以发现,在改变Uavgτ 的同时,不同的CP可调度性性能之间相对地位几乎没有改变,说明CP对于可调度性的影响比较独立。

Fig.10 Changing the system high critical level task probability CP图10 改变系统高关键级任务概率CP
6 结语
传统MCS 默认依据任务的WCETs 来安排执行预算,这种方法会产生资源过度预置问题,而一般MCS 低关键级任务执行的可靠性要求不像高关键级任务要求那么高。本文首先分析并提出了概率性需求边界函数(pDBF)模型,分析了MCS 不同模式下的pDBF,尤其是系统模式切换时结转作业的执行需求。实验表明,通过对Ci重采样或者选择合适的HT,可调度接受率可以提高32%,同时降低了pDBF模型下分析算法的复杂度。未来可采用实时接口分析(real-time interface analysis)方法,将本文方法拓展至固定任务优先级调度系统中。

