改进聚类算子的自适应多目标进化算法研究
谢倩文,何利力
(浙江理工大学 信息学院,浙江 杭州 310018)
0 引言
追求多个目标同时最优化是现代社会生活中经常发生的事,而几个优化目标在一定程度上互相排斥的情况更是屡见不鲜。因此,多目标优化问题(Multi-objective Optimization Problem,MOP)[1]研究发展迅速。多目标进化算法[2]可解决多目标优化问题,在遗传算法[3]框架下,一系列的进化算法不断发展,如差分进化算法(Differential Evolution,DE)[4]通过改进变异向量收敛于最优解;粒子群优化算法[5](Particle Swarm Optimization,PSO)通过学习鸟类捕食的群体协作行为,利用信息共享获取最优解;蚁群优化算法[6](Ant Colony Optimization,ACO)通过蚁群觅食过程中的信息素引导搜索方向,在组合优化领域取得了较好效果。这些进化算法已经广泛应用于日常生活中,如生产过程中的调度任务最优化[7],社会医疗[8]、图像处理[9]、人工神经网络优化、物流配送[10-11]以及网络安全[12]等领域中的任务优化。随着应用的深入,优化进化算法逐渐成为人工智能技术中的重要一环。因此,研究多目标进化算法对可持续发展具有重大意义。单一目标优化算法只存在单个最优解,而多个目标的优化问题需要尽可能地找到一组最优解集,多个目标优化的核心就是如何在有冲突的多个目标中找到这个最优解集。
多目标进化算法主要包括两部分:①原始种群生成子代种群,利用编码操作为每个个体赋予染色体基因,对父代基因进行交叉和变异生成子代个体;②在子代种群中挑选合适的个体组成新父代进入下一次迭代,选择算法的不同会影响最终所得个体的优秀程度。
1 研究现状
解决多目标优化问题算法主要是基于支配关系和基于分解关系。基于支配关系的算法主要以Deb[13]提出的带有精英策略的非支配排序算法NSGA-II 为主导,在所有解中找到非支配解(Non-dominated soluitons)作为Pareto 最优解(Pareto optimal Soluitons),利用拥挤距离在非支配解中找出一定数量的优秀解集。NSGA-II 在低维多目标优化问题中效果较好,但是存在搜索能力不足的问题。郑金华等[14]提出定向搜索优化策略,前期着重收敛性,后期着重多样性,兼顾了两者的平衡。为解决高维空间中拥挤距离不适用问题,NSGA-III 算法[15]利用参考点的约束支配关系找到具有更好收敛性和分布性的最优解集。这些方法证明在一些多目标问题上都有较好性能,但是在一定程度上仍然缺乏维护种群多样性能力。
基于分解方法的算法主要以Zhang 等[16]提出的基于分解的多目标进化算法MOEA/D 为主导。MOEA/D 方法初始化时先生成一组均匀分布的权重向量,将多目标问题分解成子问题,种群由每个子问题找到的最优解组成。MOEA/D 可扩展性高、收敛快、计算复杂度低,在高维空间中处理结果更理想,但是在相对复杂的Pareto 前沿情况下,解的分布性会被破坏;Li 等[17]提出MOEA/DD,将支配和分解结合剔除最差解,得到收敛良好和分布良好的点集;Yuan 等[18]提出θ-DEA,在分解的基础上利用θ支配在非支配层上选择解来提高NSGA-III 的收敛性。但随着目标个数的增加,以MOEA/D 算法为主要框架的进化算法会出现逼近Pareto前沿困难、收敛性下降、最优解选择不足等缺点,在非凸Pareto 前沿上的分布性还需要进一步优化。本文研究的主要方向是在遗传过程中通过自适应种群来定向调整进化方向以提高收敛速度,并且在收敛过程中根据权重向量的聚类算法对种群进行选择,以保护种群的多样性。
在社会生活中,多目标进化算法用来解决各种问题。针对解决多目标柔性车间调度问题,吕琳[19]提出了基于均匀设计的分配方法,提高了求解最优解的能力;周冲[20]提出基于参考点的多目标演化算法,在求解卫星星座设计问题中平衡了收敛性和多样性;赵雅卿[21]提出基于分解的多目标优化算法,在阵列天线方向中得到很好应用。
2 改进的多目标进化算法
基于分解的多目标进化算法MOEA/D 因操作执行简单且在处理许多目标测试函数时表现良好而受到青睐。在MOEA/D 算法中,有3 种分解方法可以衡量权重向量的适应度值,分别是加权求和法(Weighted Sum Approach,WSA)、切比雪夫方法(Tchebycheff Approach,TA)和基于惩罚因子的边界交叉方法(Penalty-based Boundary Intersection approach,PBI)。其中,切比雪夫方法和基于惩罚因子的边界交叉方法因为能够有效处理多目标问题而广泛应用。本文算法需要用到基于惩罚因子的边界交叉聚合方法。PBI 方法根据个体到权重向量和理想点的距离,不断收敛找到Pareto 前沿的最优解。PBI 计算公式如下:
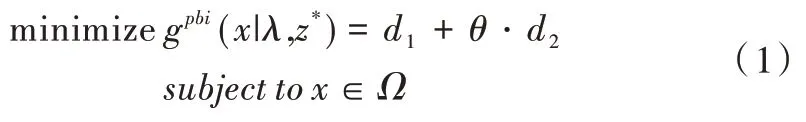
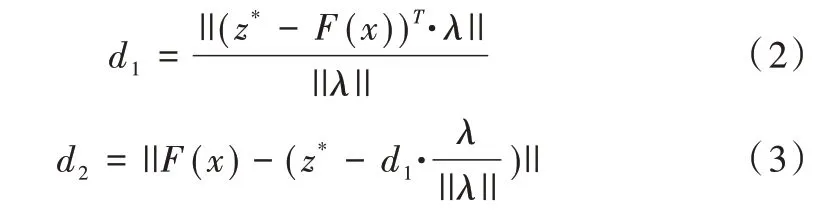
NSGA-ACM 算法利用NSGA-II 的快速非支配排序对种群进行等级排序。结合MOEA/D 的PBI 方法,加入惩罚因子θ计算gpbi值,根据gpbi选出剩余的个体。种群在迭代过程中,利用交叉变异生成子代个体,父子代合并之后根据环境选择形成新种群;若未达到最大迭代次数则继续进行下一次迭代,若达到次数则算法结束,输出最优解。算法如下:
算法1:NSGA-ACM:Frameworkofthe NSGA-ACM procedure
输入:种群迭代大小,优化问题MOP
输出:Pareto 非支配解
初始化:初始化参照点{λ1,...,λN},初始化种群N,得到初始理想点z*
whilet<max Gendo(迭代次数未达到)
Individual=Recombination+Mutation(交叉变异进化生成新个体)
Rt=N∪Individual(合并子代种群和父代种群)
Pt=EnviromentSelection(Rt)(进行环境选择)
t=t+ 1
end while
returnPt
2.1 初始化
根据Indraneel 等[22]提出的Systematic Approach 产生一组均匀的权重向量{λ1,…,λN(}N是权重向量的个数,也即种群大小),即结构化的参考点。权重向量的个数与优化目标个数m和分割数H有关,H表示在每个目标方向上的分割数,计算如下:

每个参考点满足式(5)要求,即每个参考点的各分量之和为1。从几何角度看所有参考点都落在一个平面上,即参考点是基于单位超平面产生的,且总的个数为N。

因此,初始化{λ1,...,λN}时,H的选择也需要根据公式来确定。一般来说,合适的H值可以使生成的参考点数量等于种群大小N或者略小于N。当H=m时,只会在超平面的中心多出一个参考点,超平面的其余区域是没有参考点的。然而,当m相对较大时,如m= 5,在H≥m情形下该算法会产生大量的参考点,这导致种群的数量异常庞大,从而出现进化缓慢、求解效率低下问题。所以,当H>5 时就需要采用两层权向量生成的方法,即边界层和内部层。内部层产生的权向量不能直接应用,需要收缩计算与边界层的权向量在同一个平面上,最终形成参考点集W。
假设边界层和内部层的分割数分别是H1 和H2,那么最终的参考点个数计算如下:

通过上述公式计算了边界层和内部层的参考点位置以及数量之后,内部层参考点需要进行坐标变换。假定原内部层参考点为其在第j维的目标函数值进行如式(7)的变换:

式中,τ是收缩因子,通常取τ=0.5。最后,边界层和内部层的参照点一起合并成最终的参考点集Ζ。当边界层分段数p1=2、内部层分段数p2=1 时,三维目标空间中双层参考点生成情况如图1 所示。

Fig.1 Two-layer weight vector generation method图1 两层权向量生成法
2.2 新种群生成
对于进化算法来说,生成子代种群是很重要的环节,其主要依靠遗传算法的选择操作和重组操作,而重组操作又分为交叉和变异。选择操作指从父代种群中选择个体生成子代,而重组操作则是在选择过程中根据交叉因子和变异因子定向改变父代个体,使得生成的子代个体向最优解收敛。从父代种群中随机选择两个个体p1和p2,将p1和p2进行编码,对编码基因进行交叉和变异之后生成新的子代个体c。在NSGA-II 算法中选择固定的交叉因子Pc和变异因子Pm,而这两个参数大小直接影响到种群迭代过程中生成的子代个体优秀程度。在种群迭代前期,小概率的交叉操作可以保证种群的多样性,交叉因子Pc需要小一点;当种群中优秀个体比例较高个体差异不明显之后,交叉因子Pc需要大一点。而变异操作能够避免算法陷入局部最优,种群初期提高变异概率可以加快算法的搜索速度,种群后期需要保证新种群的优秀个体不被淘汰,所以选择较小的变异概率。
为了在迭代过程中提高收敛速度并且丰富解的多样性,本文提出了自适应交叉变异策略以保证每一次的交叉和变异都是根据当前种群解的情况所得到,计算公式如式(8)和式(9)所示。
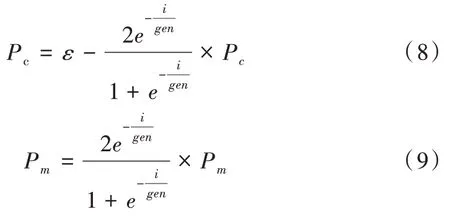
其中,Pc表示算法固定的交叉因子,Pm表示算法初始的变异因子,i表示当前的第i次迭代,gen表示算法设置的种群最大迭代次数,根据实验情况设置为1.5 时效果最好。本文采用模拟二进制交叉(SBX)和多项式变异(PM)的方法来产生子代种群。通过模拟单点二进制交叉方法,两个父代个体通过使用SBX 算子产生两个后代个体

其中,β是由分布因子η按照公式(11)动态随机决定的。η是一个自定义的参数,η值越大,产生的后代个体逼近父代个体的概率越大,建议η=1。
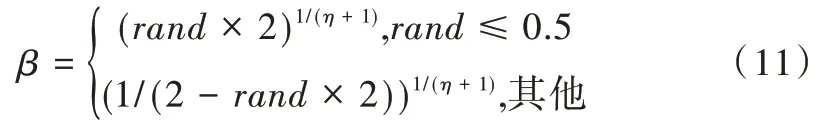
多项式变异操作使个体基因改变,提高了算法的搜索能力,计算公式如式(12)和式(13)所示。其中,i表示决策向量x的第i个分量,ai和bi分别表示第i个分量的上界和下界,pm表示变异概率,只有达到变异概率才会发生变异。

Δi的计算公式如式(13)所示。其中,随机数u是[0,1)的随机数,η是一个自定义的分布参数,为任意非负实数。遗传算法通过交叉和变异这对相互配合又相互竞争的操作使其具备兼顾全局和局部的均衡搜索能力,使算法维持群体多样性。

2.3 环境选择
环境选择的目的是选择出当前种群中符合最优条件的个体进行下一次迭代,环境选择算法如下:
算法2:Environmental Selection(R,t)
输入:解集Rt和迭代次数t
输出:下一代种群Pt+1
(F1,F1,…)=Fast-non-dominated sorting(Rt)//非 支 配 排 序
Pt+1= ∅,i= 1
while|Pt+1|+|Fi|≤Ndo//关键层之前的非支配解全部放入新种群中
Pt+1=Pt+1∪Fiandi=i+ 1
End while
Fl=Fi
if|Pt+1|≤Nthen(在关键层中选最后K 个)

将关键层中的个体根据grpipbi的值排序,Gj=
(Cji表示第i个聚集中心的第j个个体,
Gj表示所有聚集中心的第j个个体的集合)
r= 1
While|Pt+1|+|Gr|≤Ndo
Pt+1=Pt+1∪Gr(从距离参照点最近的个体开始依次放入新种群中)
r=r+1
end while (直到新种群数量为N时为止)
从Gr中随机选择N-|Pt+1|个体
end if
returnPt+1
初始化时,种群P0和第一代子代种群Q0混合形成新种群R,迭代选择从种群R开始。本文根据NSGA-II 中的快速非支配排序算法将种群R按照非支配等级进行排序。首先找出当前种群R中的非支配解集,记为第一非支配层F1,该非支配解集中的解互不支配,但是能支配不在这个解集中的其他所有解。将F1的所有解赋予非支配序号irank= 1(其中irank是个体i的非支配序值),除去第一非支配层F1之后,在剩下的种群个体中找到新的非支配解集,记为第二非支配层F2,F2中解的非支配序号在上一支配层的基础上增加为irank= 2,序号越低,解的支配优先级越高。按照上述步骤进行下去,直到整个种群分为不同支配级别的解集,同一层内的个体具有相同的非支配序号irank。将种群划分成不同等级之后,先将优先级最高的等级层中的个体放入新种群S,若放入新种群之后数量仍然小于N,则继续加入下一个优先级等级层的个体,直到S的数量大于或等于N。若加入Fl层时新种群数量大于N,则需要在Fl层中选择部分合适的个体放入S直到数量等于N,此时的Fl层称为关键层。
NSGA-II 算法在关键层中选择合适的剩余个体是通过计算关键层中个体的拥挤距离来实现的,按照从大到小依次将个体放入新种群S中。但是拥挤距离在超过3 维的多目标进化算法中选择效果不太理想,因此本文采用基于惩罚的边界交叉聚合方法来选择种群个体。对于每一个权重向量,计算该非支配层上所有个体到权重向量的gpbi值,将个体分配到具有最小gpbi值的聚簇Cj中。依次将各个聚簇中心的个体放入新种群中,直到新种群的数量为N时停止。
在生成新子代过程中,基于固定交叉因子和变异因子的多目标进化算法NSGA-II 不能根据种群的迭代情况动态调整参数,导致种群前期和后期在拥有不同占比优秀解的情况下算法搜索能力下降和收敛速度减缓。同时,在关键层使用拥挤距离来选择个体并不适合高维度优化问题,这直接影响了解在Pareto 前沿上的分布和收敛效果。本文利用改进后的自适应种群生成策略,动态地改变交叉概率和变异概率,根据种群当前的迭代情况调整进化方向,同时通过关联个体和权重向量改变个体与权重向量聚合的方法,由此选择出最后的剩余个体,形成新一代种群,有效提高算法的收敛性。通过在多目标问题测试集ZDT 和DTLZ上进行测试,NSGA-ACM 在解集的收敛性和分布性上效果更好。
3 仿真实验及分析
3.1 算法性能评价指标
参数设置见表1。
分布性(Distribution):解是否完全落在整个Pareto 前沿上,两个解之间的分布是否与Pareto 前沿的形状相适应。

Table 1 Parameter settings表1 参数设置
收敛性(Convergence):算法得到的解与真实的Pareto前沿的距离[23]显示,真实解距离Pareto 前沿越近,越能找到近似最优解。
逆世代距离(Inverted Generational Distance,IGD):表示真实Pareto 前沿中每个解到近似解中所有解的欧氏距离,从而对算法的收敛性和分布性进行评估[24]。IGD 越小表示得到的解的综合收敛效果和分布效果越好。如果IGD 值为0,则说明得到的候选解覆盖了全部真实Pareto 前沿。
3.2 算法性能测试对比
3.2.1 测试实验
本文主要在二维优化问题和五维优化问题上进行测试。在二维优化问题上,NSGA-II 和MOEA/DD 的交叉因子Pc和变异因子Pm分别设置为0.9 和1/N,而改进后的NSGA-ACM 的交叉和变异因子是根据种群的迭代次数自适应变化调整的,但Pc和Pm的初始值为0.9 和1/N。本实验选择在ZDT2 测试问题上进行对比测试。ZDT2 是非凸问题,能够较全面地测试NSGA-ACM 在Pareto 前沿的分布性和收敛性。在五维优化问题中,交叉因子Pc和变异因子Pm的设置与上述二维优化问题设置相同,对比实验选择在DTLZ问题上进行,设置最大迭代次数maxGen=300,种群大小N=300。图2 和图3 分别是算法在ZDT2 问题和DTLZ1 问题上的测试结果。

Fig.2 Test result of ZDT2图2 ZDT2 测试结果
参数初始化设置多目标问题为DTLZ1 问题,种群的最大迭代次数gen=300。

Fig.3 Test result of DTLZ1图3 DTLZ1 测试结果
3.2.2 测试结果分析
如图2 所示,NSGA-ACM 算法在二维优化问题中找到的解基本上都处在真实POF 上,并且解在中心区域和靠近坐标轴区域仍然保持着均匀分布;NSGA-II 算法中虽然大部分解都能落在POF 上,但最终的分布效果不是很理想,有待于进一步优化;MOEA/DD 算法的分布性和收敛性都不如NSGA-ACM 算法,部分解无法收敛到POF。表2为算法在测试函数上的IGD 值的平均值和标准差。从表中数据可知,NSGA-ACM 在测试函数上的IGD 值要略低于其他算法,并且在重复实验中算法的IGD 值较为稳定,上下浮动不大。在DTLZ 测试函数上,NSGA-ACM 收敛性比NSGA-II 更好,分布性比MOEA/DD 更广。综上所述,NSGA-ACM 在二维以及五维优化问题上的实现效果优于MOEA/DD 以及NSGA-II。

Table 2 IGD mean and standard deviation of each algorithm of diffevent test functions表2 在不同测试函数上各算法的IGD 的平均值和标准差
4 结语
NSGA-ACM 算法采用自适应种群的交叉因子和变异因子定向调整种群迭代方向,在种群初期增强种群的多样性,在迭代后期又能维护种群的多样性,此种改进方式使得算法能够搜索到更加符合真实Pareto 前沿的最优解。在PBI 方法的基础上通过个体与参考点关联策略,将个体放在参考点的聚簇中,找出剩余最优解,提高了算法的收敛性。在二维测试函数上进行测试实验,对比分析显示该算法不仅能够收敛于Pareto 前沿,还能保证完全覆盖Pareto前沿以及在Pareto 前沿上均匀分布。从各项实验数据可知,NSGA-ACM 算法在二维和五维空间中,与NSGA-II、MOEA/DD、NSGA-II 这3 个算法对比都能展示出更优越的性能,在均匀分布性以及收敛性方面都得到了改善。

