贪心算法在智能导检中的应用研究
付 冰,周作建,张维芯
(1.南京中医药大学人工智能与信息技术学院,江苏 南京 210023;2.江苏省中医院信息数据中心,江苏 南京 210004)
0 引言
随着医学模式向预防为主的健康管理方向转移,人们愈发重视早期筛查慢性病,全社会强调为实施健康中国落实以预防为主的发展战略,将中心由“治已病”向“治未病”转变,加强疾病预防和健康促进研究[1-2]。随着2020 年全球新型冠状病毒疫情爆发,人们更加重视大健康产业,同时在人口老龄化趋势下,体检需求日益增加,驱动健康体检行业规模迅速扩容[3-4]。
体检需求日益增加使健康产业蓬勃发展,随着体检中心客户人数剧增,体检排队时间大大增加,而候诊时间是客户评价满意度的主要指标之一[5-6]。杨一帆[7]运用排队论建立了病患等待时间的区间估计模型。李凌洋等[8]通过引入M/M/c/∞/∞/FCFS 排队模型,构建基于排队论的医院收费窗口设置优化模型,以患者最少等待时间和最低经营成本为目标设置窗口。Kaungu 等[9]采用多通道排队方法M1/M2/S/n/FCFS 开发模型,该模型提供了多种性能指标优化系统。以上学者都是通过增加服务窗口数量的方式缓解排队压力,但随之增加了运营商服务成本[10],并且存在服务资源浪费的情况[11]。因此需要合理的动态规划项目顺序方案。魏伟等[12-13]基于筛选路径选择策略,实验结果显示LTP 策略在考虑正在接受服务人数、排队等待人数等病人实时状态时效果最好。梁月等[14-15]在此研究基础上将人数进一步规划为时间,基于排队论理论设计了4 种排队方案,并进行动态规划仿真实验,实验结果显示在不同排队策略影响下,排队时间及逗留时间不同。通过对比分析表明,综合考虑排队等待时间、服务时间等因素的方案最优。刘路[16]提出了实时通知策略,依据当前时间结点优先安排完成时间最早的检查,并进行动态规划检查路径。陈家伟[17]以最短行进时间为目标,结合TSP 模型构建问题的整数规划模型,并利用混合粒子群算法进行求解。
目前智能导检路径规划研究仍处于早期阶段,众学者将重心放在规划服务窗口上,而对健康体检的路径选择策略及规划待检项目整体顺序方向的研究较少。研究表明,通过调整客户检查顺序的路径选择策略可有效缩短排队时间[12],本文对上述学者的路径选择策略进行改进,最终设置了考虑服务时间、排队时间和路程时间的路径规划策略,同时考虑客户预测待检行程方案,为体检排队的智能化、自动化研究提供新的思路。
1 相关知识
1.1 插值拟合
插值是离散函数逼近的重要方法之一,可通过函数在有限个点处的取值情况,估算函数在其他点处的近似值[18],用来填充图像变换时像素间的空隙。最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配,使拟合数据与实际数据之间的SSE 为最小值。计算方式如式(1)所示:

其中,ω=[ω1,ω2,…,ωn]T为待定参数,为了寻找函数f(x,ω)的参数ω的最优估计值,对给定m组观测数据求解目标函数。
拟合优度是一种统计方法,基于所得观测值作出预测[19]。度量拟合优度的统计量为R-square(R2)及SSE。具体公式如下:

其中,R-square 是衡量整体拟合度的重要指标,当值越接近1 时,拟合程度越好;SSE 数值越小则代表拟合程度越好。
1.2 贪心算法
贪心算法是一种能够得到某种衡量方式下最优解的分级处理方法,采用自顶向下、以迭代方式进行贪心选择,每次贪心选择便会将问题简化为规模更小的子问题[20]。算法思路为建立数学模型描述问题,并将求解问题分为若干个子问题,先取得子问题的局部最优解,然后将子问题的局部最优解合成为原问题的一个解。因此,贪心算法能够筛选出当前的最优解,并未考虑整体最优性,所取得的仅是在某种意义上的局部最优解。但贪心算法的计算过程更为迅速、简便[20-21],并且局部最优解的计算结果与整体最优解的求解结果较为接近。袁绛书等[22]利用贪心算法构建景区路径规划模型,依托游客对各景点的个性化选择,考虑游客景点偏好、金钱预算、精力等多重约束条件,以此规划游客最满意的路线。王翔[23]基于贪心算法不断推算局部最优解,对采矿进行动态规划,选取多重规划状态下的路径方案进行对比,最终取得最优策略。蔡文洁等[24]将贪心算法与随机算法相结合,快速取得不同情况下初始排班表的最优解,以满足个性化需求。
2 基于贪心算法的智能导检模型
2.1 导检问题描述
体检中心设有若干检查项目,相同检查项目时间大致恒定。以体检客户角度出发,由于客户可个性化选择体检套餐,不同项目的等待时间和服务时间均存在差异。具体问题描述如下:①体检客户到达体检中心的时间随机;②体检客户检查的项目具有多样性;③不同项目的服务时间存在差异;④不同科室服务台数量不同;⑤不同科室之间的距离不同。综上所述,体检中心需为体检客户预先分配合理的检查顺序,使体检客户逗留的时间最短。
2.2 智能导检模型构建
步骤1:采用MATLAB 的griddata 函数模拟体检中心的排队状态,通过图1-图2 形象的表示不同科室在不同时间节点的人数密度和时间密度。其中,横坐标分别表示眼科、心电图室、妇科、外科(女)、口腔科、耳鼻喉科、内科、外科(男)、血液科、彩超甲状腺、彩超肝胆胰脾双肾前列腺、胸部正位片DR 室、胸部CT。纵坐标为7:30-11:30,间隔30min 进行统计的时间点信息,竖坐标为当前时间某一科室的等待人数,图2 竖坐标为当前时间某一科室总体的等待时间。

Fig.1 Griddata v4 interpolated waiting number图1 griddatav4 插值等待人数

Fig.2 Griddata v4 interpolation waiting time图2 griddata v4 插值等待时间
步骤2:通过最小二乘法进行数据拟合,构建体检项目到达率φi(t)与时间t的函数关系。由表1 可见,数据拟合的SSE 值分别为5.115、0.787 8、4.541、1.304 等,R-square 值分别为0.979 6、0.996 7、0.898 6、0.996 4 等,表明该方法取得了较好的拟合效果。
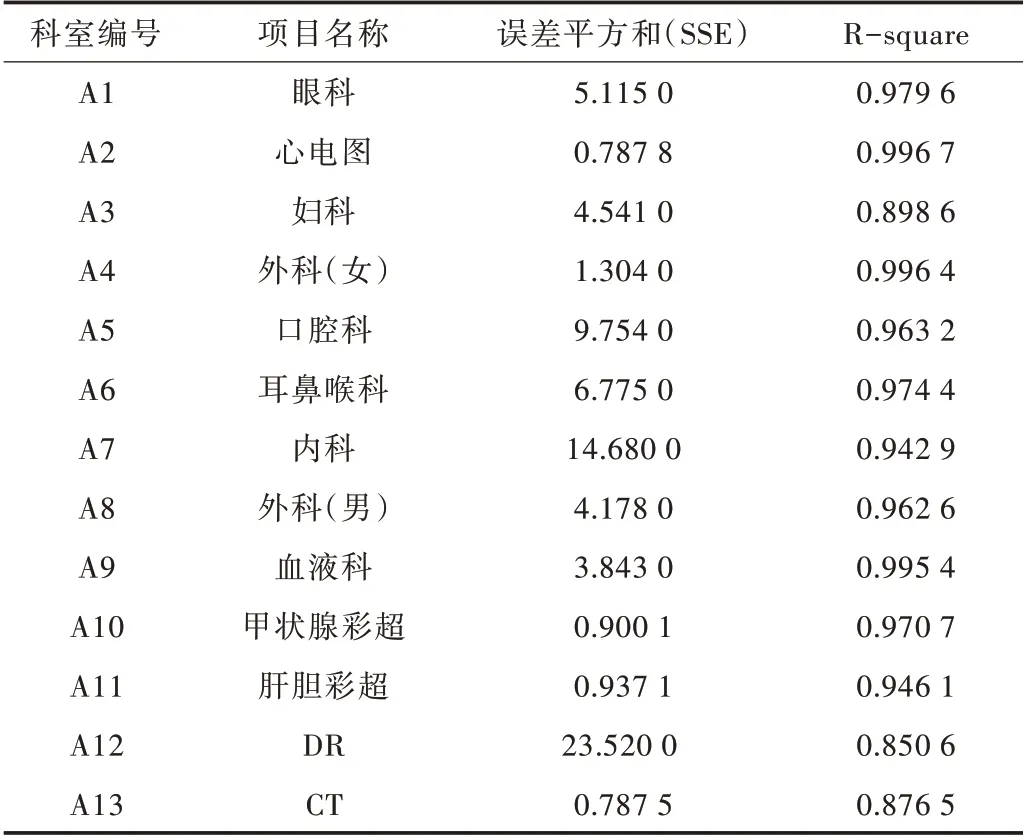
Table1 Evaluation index of goodness of fit表1 拟合优度评价指标
步骤3:根据式(6)计算当前队列中待检人数。其中,Pi(k-1 )为上一时间段剩余的待检人数为时间区间为[k-1,n]时的到检人数,Mi为服务时间。
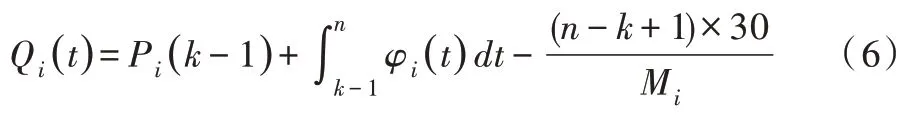
步骤4:计算d(i,j)表示科室i到科室j 行走的距离,如式(7)所示。其中,科室i的坐标为Ci(ai,bi)。

步骤5:计算待检项目中服务时间、排队时间和路程时间三者的总时间,计算公式如式(8)。
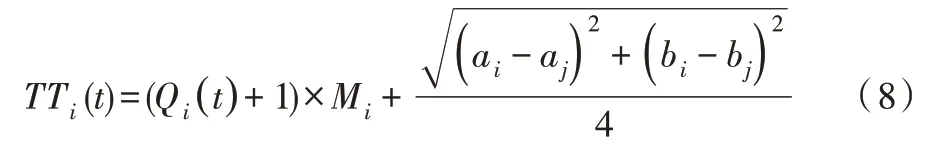
步骤6:采用贪心算法在时间t时对TTi(t)进行全局比较,选择min(TTi(t))为局部最优解,然后重新计算时间点,不断合成待检项目局部最优解后形成体检路径。
3 实验结果与分析
3.1 数据来源
数据来源于江苏省中医院体检中心,选取2021 年3 月份13 个科室全部的体检数据,以30min 为间隔统计体检中心客户的到达情况,过滤掉不完整、无意义的数据后,最终选择29 126 条数据作为研究对象。如表2 可见,13 个科室分别为眼科、心电图室、妇科等。时间按照“7:30-8:00”“8:00-8:30”“8:30-9:00”等区域进行划分,为了便于统计分别赋值为1-8。

Table 2 Experimental data structure表2 实验数据结构
3.2 结果分析
如表3 所示,将拟合的函数采用贪心算法构建智能导检模型,根据不同初始数据,以体检客户个性化选择为基础,加入体检项目服务时间的各异性因素,并考虑顾客切换不同项目时所消耗的时间成本,将不同科室之间距离量化为时间。
如图3 所示,通过对体检客户个性化设置到达时间及服务套餐,应用贪心算法自顶向下以迭代方式相继进行贪心选择,最终预测体检项目顺序及计算总体等待时间,获得体检客户的路径状态。由表4 可见,当预设体检客户A体检的时间为9:24,选择套餐一(女)项目分别为A1、A2、A3、A4、A5、A6、A7、A9、A10,通过智能导检模型规划体检顺序及预测体检时间,可预测其逗留时间为120.56min。

Table 3 Distance time between departments表3 各科室之间距离时间
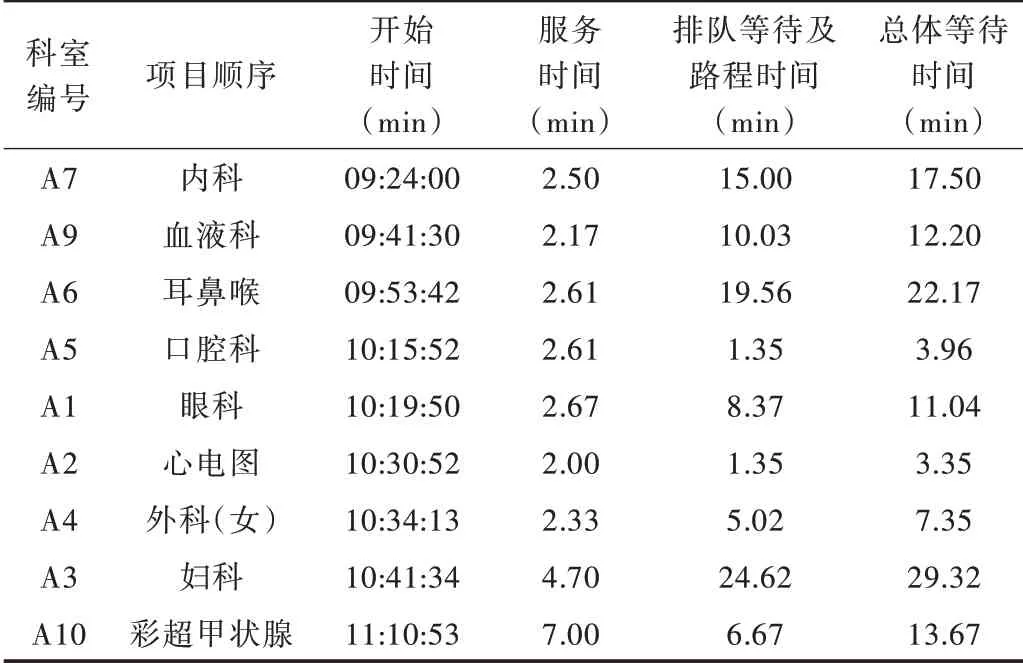
Table 4 Sequence planning of item A of health checkers表4 体检客户A 项目顺序规划

Fig.3 Sequence path diagram of physical examination items图3 体检项目顺序路径
将提出的SQJI 路径选择策略与SQI、SQA、QI、QA、SI 和SQJA 路径选择策略进行对比分析。其中,SQI 与SQA 分别表示为以体检服务时间与排队时间之和最小值或最大值作为评价标准;QI 与QA 分别表示为以排队时间最小值或最大值作为评价标准;SI 表示以服务时间的最小值作为评价标准;SQJI 与SQJA 则分别表示以服务时间、排队时间及路程时间之和最小值或最大值作为评价标准。对比结果如图4 所示,实验证明SQJI 路径选择策略可有效减少客户逗留时间。如表5 可见,在1-5 及1-8 时间区间SQJI 优越性更强,客户逗留的时间最少。
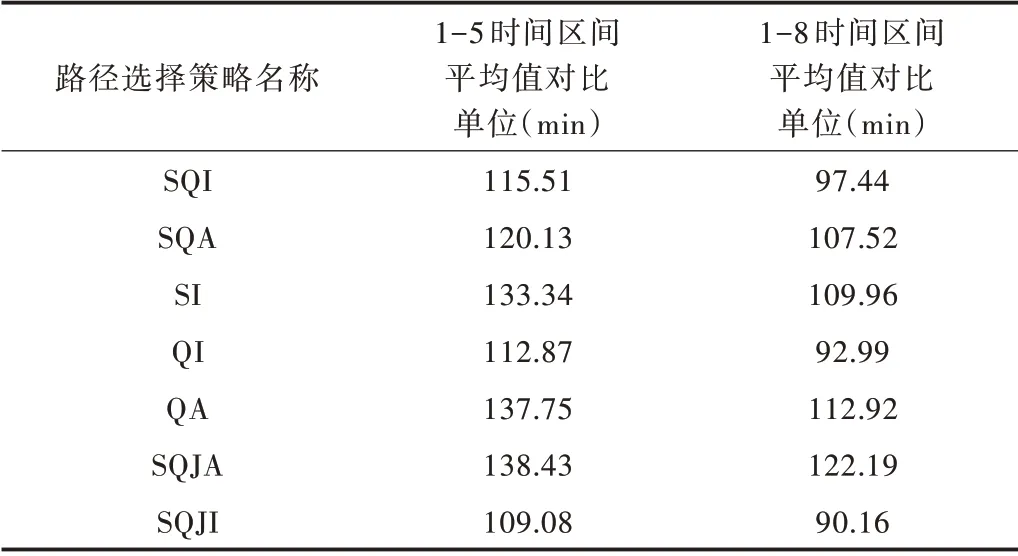
Table 5 Comparison between 1-5 and 1-8 time intervals表5 1-5 与1-8 时间区间对比

Fig.4 Comparison of experimental results of different path selection strategies图4 不同路径选择策略模型实验结果对比
4 总结
目前关于多检查科室组成的多服务台排队问题的研究仍然较少,当前优化排队时间的主流方式为合理规划服务窗口的数量,具有一定的局限性。因此,本文提出基于贪心算法的智能导检路径优化模型,以规划客户体检项目顺序。在考虑服务时间、排队等待时间的基础上增加了科室距离因素,将距离信息量转化为时间信息,利用贪心算法寻找最优解并采用分级处理方法构建最优体检路径。本文方法在一定程度上弥补了部分中小型体检中心无法合理规划服务台数量的局限性,将路径选择策略与贪心算法相结合,预测体检路径及等待时间,并显示各时间节点的信息量。下一步将考虑加入跨区域因素,综合考虑科室的地理区域,以提升模型的实用性。
——国外课堂互动等待时间研究的现状与启示

