基于2DPCA 特征降维的CNN 说话人识别
张学祥,雷菊阳
(上海工程技术大学机械与汽车工程学院,上海 201620)
0 引言
在信息时代下,智能化产品的市场需求强劲[1]。语音识别技术通过让机器学习人类语言搭建起人机交互的桥梁。其中,说话人识别技术在人机交互领域更是发挥着举足轻重的作用。其通过挖掘说话人语音中特有的声纹信息实现对说话人身份的判别,是一种重要的身份认证手段。说话人识别需要从语音中提取说话人的声学特征,并建立话者模型以获得识别结果[2]。目前说话人识别建模方法包括混合高斯模型[3]、隐马尔科夫模型[4]、神经网络等。近年来,随着计算能力的提高与大数据的出现,深度神经网络被广泛应用于说话人识别领域[5-6]。值得注意的是,深层网络模型的识别性能很大程度取决于大批量训练数据[7]。如果直接使用这些数据进行模型训练,不仅时间成本较高,而且会导致信息冗余,不利于说话人身份鉴别。为减少模型的训练时间成本,同时提高说话人识别系统性能,有必要对训练数据进行后续处理。
1 相关研究
原始语音信号经过预处理后再进行特征提取,才能作为匹配模型的训练数据。LPCC 特征(Linear Prediction Cepstrum Coefficient,LPCC)是常见的声学特征之一,其通过模拟人的发声机理分析与预测语音基本参数特征,对浊音具有较好的识别效果,但对鼻音及清音的识别效果较差[8];MFCC 特 征(Mel Frequency Cepstral Coefficients,MFCC)采用一组梅尔频率滤波器组描述人耳对频率的感知特性,因而具有更好的判别效果[9]。然而,在MFCC 特征提取过程中的DCT 降维操作会导致一些有效信息损失。为此,本文在特征提取过程中放弃了DCT 操作,而直接采用语音信号的梅尔频率能量系数特征(MFEC 特征)。全连接深度神经网络(DNN)具有强大的数据分层学习能力,可提取更为抽象、稳定的数据特征。文献[10]提出的d-vector 说话人识别系统使用预先训练的DNN 作为特征提取器,选取网络最后一层隐层的输出激活值作为d-vector 特征,利用后验分类模型实现说话人识别,但基于DNN 的话者模型无法有效对语音特征中的局部时间及频谱相关性进行建模;文献[11]中采用CNN 取代DNN 网络建立话者模型,利用余弦距离进行说话人识别,取得了更好的实验效果。尽管采用话语级特征作为CNN 网络的训练样本,经过多次训练即可获得良好的识别效果,但语音之间存在时长差异,若要获得同等大小的特征,需要进行裁剪或补零,因而导致数据失真,影响识别效果。采用帧级特征用于模型训练虽然可避免输入大小不一的情况出现,但语音帧之间的相关性会导致帧级特征信息冗余,不仅影响神经网络识别性能,而且使网络训练难度增大,收敛速度慢。
根据以上研究背景,本文提出基于2DPCA 特征降维[12]的CNN 说话人识别方法。该方法采用帧级特征矩阵作为卷积神经网络训练数据,利用2DPCA 对帧级特征矩阵进行特征降维,舍去帧级特征矩阵中的冗余信息,同时保留特征参数中的有用信息,使得说话人的个性特征分布更为集中,从而提高说话人识别性能及收敛速度。
2 降维分析
2.1 帧级特征提取
MFEC 特征可作为帧级语音信号的数据表示。相比于MFCC 特征,MFEC 特征具有更高维度,同时特征之间的相关性也较强,在频谱上表现更为平滑,通过CNN 网络的自适应特征学习可很好地利用这种相关性。
MFEC 特征提取过程如图1 所示。首先对说话人语音样本进行分帧操作获得帧级数据,然后对帧级数据提取帧级特征,取相同数量的帧级特征即可组合成同等大小的特征矩阵。由于每段语音时长各不相同,因此每段语音获得的特征矩阵数量也不相同。本文中帧长为20ms,帧移为10ms,对每个帧级语音信号提取40 个MFEC 特征参数,取连续60 个帧级信号对应的MFEC 特征参数叠加组合成60×40 的MFEC 特 征 图。
2.2 2DPCA 降维
采用60×40 的MFEC 特征矩阵作为CNN 训练数据,训练强度大,训练时间长,同时特征信息冗余,不利于提高系统识别性能。本文采用2DPCA 对MFEC 特征矩阵进行降维处理,2DPCA 在PCA 基础上进行了改进,可直接利用原始图像矩阵构建协方差矩阵[12-13]。相比于PCA 降维,使用2DPCA 更容易评估协方差矩阵,同时由于构建的协方差矩阵维数变小,计算特征向量的复杂度将降低[14]。2DPCA 通过式(1)将特征图像矩阵A∈Rm×n投影到空间X∈Rn×d上,得到图像矩阵A的投影特征向量Y∈Rm×d,完成特征降维。


Fig.1 MFEC feature extraction图1 MFEC 特征提取
2DPCA 降维首先利用投影样本的总体散布矩阵求解变换矩阵X,投影样本的总体散布矩阵可用特征向量Y协方差矩阵的迹表示:

其中,Sx表示特征向量Y的协方差矩阵,具体如下:

故协方差矩阵的迹为:

则图像的协方差矩阵可表示为:
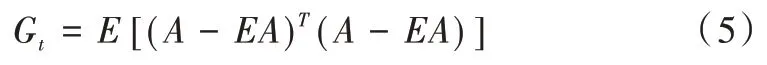
投影样本的总体散度矩阵与图像协方差矩阵关系如下:

约束准则公式如式(7)所示,根据该公式选取一组最优的投影轴X1,X2,…,Xd,使得投影样本的总体散度最大化,即选取Gt前d个最大特征值对应的特征向量,则图像A经过变换矩阵X= [X1,X2,…,Xd]转换后的特征图像Y最优。

假设一个样本集中包含N个不同话语的语音特征图,特征图大小为m×n,则图像的总体散布矩阵为:

其中,为训练样本均值。
首先求Gt的特征值并选取最大的d个特征值,将与之对应的标准正交特征向量组成投影矩阵X,则图像Ai通过式(1)投影到空间X上即可得到一组投影特征向量Y1,Y2,…,Yd;然后将这些投影特征向量组合成一个m×d的矩阵,也即图像Ai的特征图像矩阵Bi={Y1,Y2,…,Yd} ;最后将样本集中所有图像通过2DPCA 降维得到的特征图像集B= [B1,B2,…BN]作为CNN 网络学习数据。
3 基于2DPCA 特征降维的CNN 说话人识别方法
本文提出的基于2DPCA 特征降维的CNN 说话人识别方法主要在传统CNN 说话人识别方法基础上进行了改进,其输入采用说话人语音的帧级特征形式,同时利用2DPCA对提取到的MFEC 特征矩阵进行降维处理,从而获得更有效的特征矩阵作为CNN 的输入数据,并通过CNN 的自适应特征学习创建说话人模型。该方法不仅可有效利用特征之间的相关性,而且可提高CNN 模型收敛速度。
3.1 卷积神经网络
CNN 在传统多层神经网络基础上增加了局部连接的卷积层与池化层,通过多层卷积操作可提取不同层级特征,池化层对输入特征图的子抽样操作可有效降低特征维度[15-16]。相比于传统神经网络,CNN 能够直接对图片数据进行特征提取,而不需要经过数据重构。通过模拟具有局部感受野特性的人类视觉细胞进行特征提取,可进一步提高特征检测效果。在说话人识别任务中,卷积运算由于具有平移不变性,可提高系统泛化能力,因而在处理多样性语音信号时更具优势。其卷积过程可表示为:
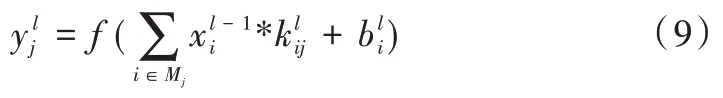
其中,表示第l- 1 层的第i个特征图;是卷积核,*是卷积操作,是与卷积层第j个特征图建立关系的前一层特征图集合,b是偏置项,f是非线性激活函数。引入非线性激活函数的目的是利用非线性激活函数对特征的变换,增加网络处理非线性复杂问题的能力。与传统CNN 不同,本文使用PReLU 激活函数替代ReLU 函数。PReLU 函数是在ReLU 函数基础上发展而来的,当其为负值时则导数不再为0,从而避免了网络陷入“ReLU 死区”[17]。其函数表达式如下:

池化层对卷积特征图进行子抽样操作后,特征图数量保持不变,但图片维度会降低,因此可防止过拟合。采样过程可表示为:

式中,down()代表下采样函数,用于计算上一层特征图中相邻区域的最大值。
3.2 网络结构设计
本文采用经典的AlexNet 体系结构[18]进行实验,网络包括1 个输出层、3 个连续的卷积池化结构、2 个单独的卷积层、2 个全连接层及1 个Softmax 层。网络结构参数设计如表1 所示。模型输入为60×40 的MFEC 特征矩阵,经2DPCA 降维后输入大小为60×20。网络采用自适应初始化器对卷积核权值参数进行初始化,损失函数采用交叉熵损失函数,并利用Adam 优化器进行参数优化。初始学习率为0.001,总迭代次数为200 次。前100 次迭代以后,每迭代10 次学习率降低10%[19]。为防止过拟合,设定前两个全连接层为丢弃层,丢弃率为50%,同时将PReLU 激活函数应用于卷积层与前两个全连接层来训练该模型,最后一个Softmax 层用于说话人预测分类[20]。
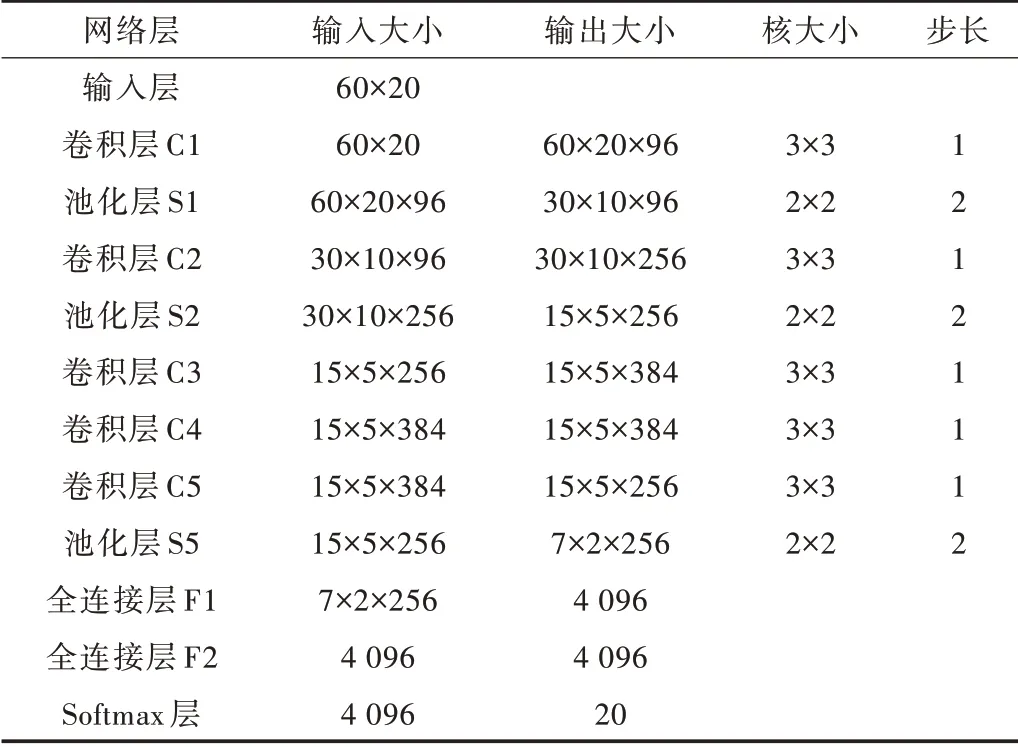
Table 1 AlexNet network structure design表1 AlexNet 网络结构设计
3.3 算法流程
本文提出的说话人识别算法步骤如下:
方法:基于2DPCA 特征降维的CNN 说话人识别方法
输入:说话人语音数据集
Step 1:预处理。对短语音信号进行分帧处理,提取帧级信号的40 维MFEC 特征,将连续60 帧帧信号提取到的MFEC 特征组合成60×40 语音特征图。
Step 2:使用2DPCA 将每张60×40 的MFEC 特征图降维成60×d的特征矩阵。①根据式(8)定义图像的总体散布矩阵Gt;②求最优投影轴X1,X1,…,Xd,即选取Gt前d个最大特征值对应的特征向量;③利用式(1)对图像A作投影特征变换,获得一组投影特征向量Y1,Y2,…,Yd;④将投影特征向量组合特征矩阵B= [Y1,Y2,…,Yd]作为CNN 网络的输入。
Step 3:选取70%的训练数据作为训练集,其余为测试集。
Step 4:CNN 网络参数初始化,包括CNN 结构、卷积核参数、学习率、批大小N和迭代次数。
Step 5:CNN 网络训练
for i= 1:迭代次数
for j=1:批数量
在训练数据集中抽取N个训练数据输入到CNN,前向传输计算在当前网络权值与输入下的网络输出;
反向传播调整权值;
更新权值;
end for
end for
Step 6:CNN 网络测试,将预测结果与样本标签进行比较,获得预测准确度。
4 实验结果与分析
4.1 实验数据集
实验数据集采用Primewords Chinese Corpus Set 1 语料库进行模型训练与测试。Primewords Chinese Corpus Set 1数据集是由上海元语信息科技有限公司推出的汉语普通话语料库,包含100h 的语音数据,由296 名来自中国不同区域的说话人录制而成。该数据库中的音频文件多为安静环境下录制,采样频率为16kHz。本研究从中随机挑选出男性、女性各60 人,每人50 条语句(每条语句时长约为6s)。其中,100 人语料集用于背景模型训练,其余20 人语料集用于系统测试。系统测试时,选择每个人前70%的数据用于模型训练,剩下30%的数据用于系统测试。
4.2 实验结果分析
4.2.1 批大小选择
为节省模型训练开支,需要选择合适的批大小。一般来说,批大小越小,网络收敛速度越快,但会导致训练时间变长,并且当批大小过小时,网络可能无法收敛。增大批大小可使网络处理相同数据量的时间缩短,但收敛速度会下降,收敛时所需的迭代次数也将增多。根据3.2 节介绍的模型参数设置,改变批大小并进行多次重复实验得到的损失值曲线如图2 所示。

Fig.2 Loss value curve during model training图2 模型训练过程中的损失值曲线
从图2 可以看出,当批大小为50 时,网络收敛速度最快,但是训练震荡较大;当批大小为85 时,收敛速度稍微减慢,训练震荡也有所减小,损失值稳定状态位置基本保持不变;当批大小继续增大时,收敛速度变得更加缓慢,同时训练损失的稳定值也变大。综上考虑,本文选择批大小为85。另一方面,从图中可发现,训练损失值在第150 次迭代后基本趋于稳定,因此为了不浪费训练时间,设置迭代次数为150 次。
4.2.2 特征维数影响
从表2 可以看出,刚开始随着特征维数的增大,说话人识别系统的识别率也逐渐提高,并且在维数较小的情况下,识别率提高的速度快。维数越大,识别率提高的速度越慢。当特征维数为20 时,系统识别率达到最大值。继续增加特征维数,系统识别率反而有所下降,但是逐步趋于稳定。这是因为特征维数过大而造成的信息冗余抑制了说话人个性信息,导致识别率降低。因此,本文选择特征维数d= 20,此时有效信息的损失最小,在不影响识别性能的情况下,训练数据得到了有效压缩。

Table 2 Effect of feature dimension on speaker recognition performance表2 特征维数对说话人识别性能的影响
4.2.3 与其他说话人识别方法比较
为测试基于2DPCA 特征降维的CNN 说话人识别方法的优越性,作为对比,在相同数据集的条件下,选取CNN(话语级特征)话者模型和CNN(帧级特征)话者模型作为本文的基线实验。其中,话语级特征选择语谱图特征形式,实验结果如图3 所示。3 种算法识别性能比较如表3 所示。

Fig.3 Recognition rate change of different algorithms图3 不同算法识别率变化

Table 3 Comparison of recognition performance of three algorithms表3 3 种算法识别性能比较
从表3 可以看出,本文提出的2DPCA 特征降维的CNN说话人识别方法明显比其他两种方法运行速度快,相比于CNN(话语级特征)方法与CNN(帧级特征)方法,运行时间分别减少了57%和36%,同时识别率也有所提高,说明使用2DPCA 技术对帧级特征进行降维处理可有效减少冗余信息,在保证系统识别性能的同时,大幅缩短了网络运行时间。
5 结语
本文提出一种基于2DPCA 特征降维的CNN 说话人识别方法,该方法通过2DPCA 对帧级特征进行特征降维处理,将降维后的特征矩阵用于CNN 网络训练与测试,在保证识别率的同时,大幅降低了CNN 网络的运行时间成本。实验数据表明,该方法运行速度明显优于传统的CNN 网络说话人识别方法,同时系统识别率也有所提高。该方法对于说话人识别的理论研究具有重要的参考价值,在接下来的研究中,将考虑使用不同结构的网络模型进一步发掘该说话人识别方法的潜能。

