保水开采覆岩等效阻水厚度的内涵、算法与应用

张东升，范钢伟,，张世忠，马立强，王旭锋

(1.中国矿业大学 煤炭资源与安全开采国家重点实验室，江苏 徐州 221116；2.中国矿业大学 矿业工程学院，江苏 徐州 221116)

近年来，煤炭开采过程中的水资源保护问题越来越引起国家的重视和关注，国家能源发展“十二五”和“十三五”规划、煤炭工业发展“十二五” 和“十三五”规划都明确提出“积极推广煤矿保水开采技术”的要求。回顾过去，传统大规模、高强度、粗放式的煤炭开采，极易造成覆岩裂隙大面积扩展、导水通道大区域连通及覆岩隔水性能严重丧失等，进而引发水资源流失、河流干涸、植被退化等一系列生态环境问题。特别是对于我国煤炭开采的主产区——西北部矿区，一方面煤层埋藏浅、厚度大，地层成岩时间晚、强度低；另一方面气候干旱、水资源匮乏、生态环境脆弱，地表水和浅层地下水更是维系矿区生态稳定和矿井正常生产的宝贵资源。煤炭开采与水资源保护之间的矛盾一直是制约我国西北部矿区矿井生产的主要问题之一。因此，最大程度地减少煤炭开采对水资源和生态环境的影响，实施保水采煤，既是国家生态环境可持续发展的战略要求，也是矿井绿色、环保、协同开采的迫切需求，而保水采煤可行性的准确判别和有效预测则是开展矿井保水开采科学设计的提前和基础。

针对保水采煤可行性评判，前期研究主要集中在覆岩导水裂隙带高度、有效保护层厚度及隔水层采动稳定性等方面。马立强等以榆神矿区实际地质条件为基础，得到了覆岩导水裂隙带发育高度与有效保护层厚度，进而确定出矿区能够实现保水采煤的最大采高；徐智敏等针对新疆哈密干旱矿区侏罗系煤系地层，得到了覆岩采动导水裂隙发育的裂采比及整体形态特征，在此基础上对研究区保水采煤可行性进行了评价；许延春提出“有效隔水厚度”评价方法，进而确定水体下综放开采保护层最小有效隔水厚度；李涛等发现潜水水位降深与有效隔水土层厚度有直接关系，并给出了典型地质条件下能够实现保水采煤的最小保护层厚；黄庆享等认为覆岩“上行裂隙”和“下行裂隙”是影响隔水层稳定性的主要因素；姚邦华等采用能量法得到了隔水层采动变形的挠度及应力表达式；孙建等以应力和应变为衡量指标，推导出覆岩结构隔水层及上方黏性土层稳定性力学判据。上述研究给出了保水采煤的一些具体判别方法及相关指标，有效指导了部分矿井的保水开采实践。笔者团队提出了采动覆岩阻水能力是由结构阻水和水理阻水特性共同决定的。特别是对于我国西北矿区广泛分布的弱胶结地层而言，其富含蒙脱石、伊利石、高岭土等黏土矿物，具有良好的遇水膨胀、泥化特性，能够有效弥合部分采动裂隙而表现出良好的隔水性能自修复现象，出现实测中导水裂隙带高度难以判定而无法指导保水开采工程实践的情形。

在上述研究的基础上，笔者从覆岩整体阻水性能角度出发，考虑采动各岩层渗透性变化及其与变形之间的关系，建立采动覆岩等效渗透系数计算方法；同时以覆岩垂向渗流速度与含水层补给速度相等为临界条件，得到采动覆岩能够实现保水采煤的最大临界渗透系数；在此基础上，提出覆岩等效阻水厚度计算方法，并给出实现保水采煤的定量判定条件。

1 覆岩等效阻水厚度的科学内涵

受开采扰动，隔水岩层(组)阻水性能丧失是造成地下水流失、水位下降的根本原因，其本质是上覆岩组渗透率的增大。这是开采造成顶板至目标含水层之间的所有岩组共同发生变形、移动、破坏而渗透性发生变化的结果，亦即覆岩组的整体渗透性。因此考虑基于地层岩石特性(包括岩石孔隙率、渗透率等)、煤层埋深、煤层-含水层间距等因素，从采动覆岩整体阻水性能角度出发，以覆岩等效渗透系数为基础，提出将煤层顶板至目标含水层之间的所有岩层虚拟为一层等效阻水层的学术思想，如图1所示。通过计算该虚拟阻水层的“等效阻水厚度”来定量评价保水开采的可行性。

图1 等效阻水厚度内涵示意Fig.1 Connotationof equivalent water resisting overburden thickness

基于覆岩等效渗透系数确定的等效阻水厚度，可以反映开采过程中覆岩结构的阻水效应和隔水岩层的水理特性，综合考虑覆岩整体的阻水行为与地下水系统的动态响应之间的关系，为保水开采预测评价、方法选择和参数优化提供新的思路和方法。

2 采动覆岩等效渗透系数计算方法

岩层渗透系数是表示采动覆岩阻水性强弱的重要指标之一。研究表明采动覆岩渗透系数变化具有明显的分区性，具体表现为：采动覆岩不同岩层渗透性不同；同一岩层不同区域渗透性也不相同，同时垮落带及工作面两端头覆岩存在明显的渗透率增高区，如图2所示。考虑到采动覆岩渗透性变化有很强的分区性，将采动覆岩等效渗透系数的计算分为单一岩层等效渗透系数和覆岩整体等效渗透系数计算2部分。由于垮落带内岩块呈不规则堆积状态，其渗透系数往往为初始渗透系数或完整岩层的10～10倍甚至更高，因此认为覆岩垮落带内的岩层不具有隔水能力。同时本文对覆岩等效渗透系数的计算以垮落带上方至目标隔水层之间的岩层为研究对象。

假设采动覆岩垮落带上部岩层在结构阻水和水理阻水的共同作用下，其垂向渗流符合达西定律，同时忽略采动覆岩各岩层的厚度变化，对于垮落带上方至目标隔水层之间的岩层(岩层序号～)，其垂直于层面渗流的等效渗透系数表达式为

(1)

式中，为岩层垂直于层面方向的等效渗透系数；为单层岩层的厚度；为单层岩层的渗透系数。

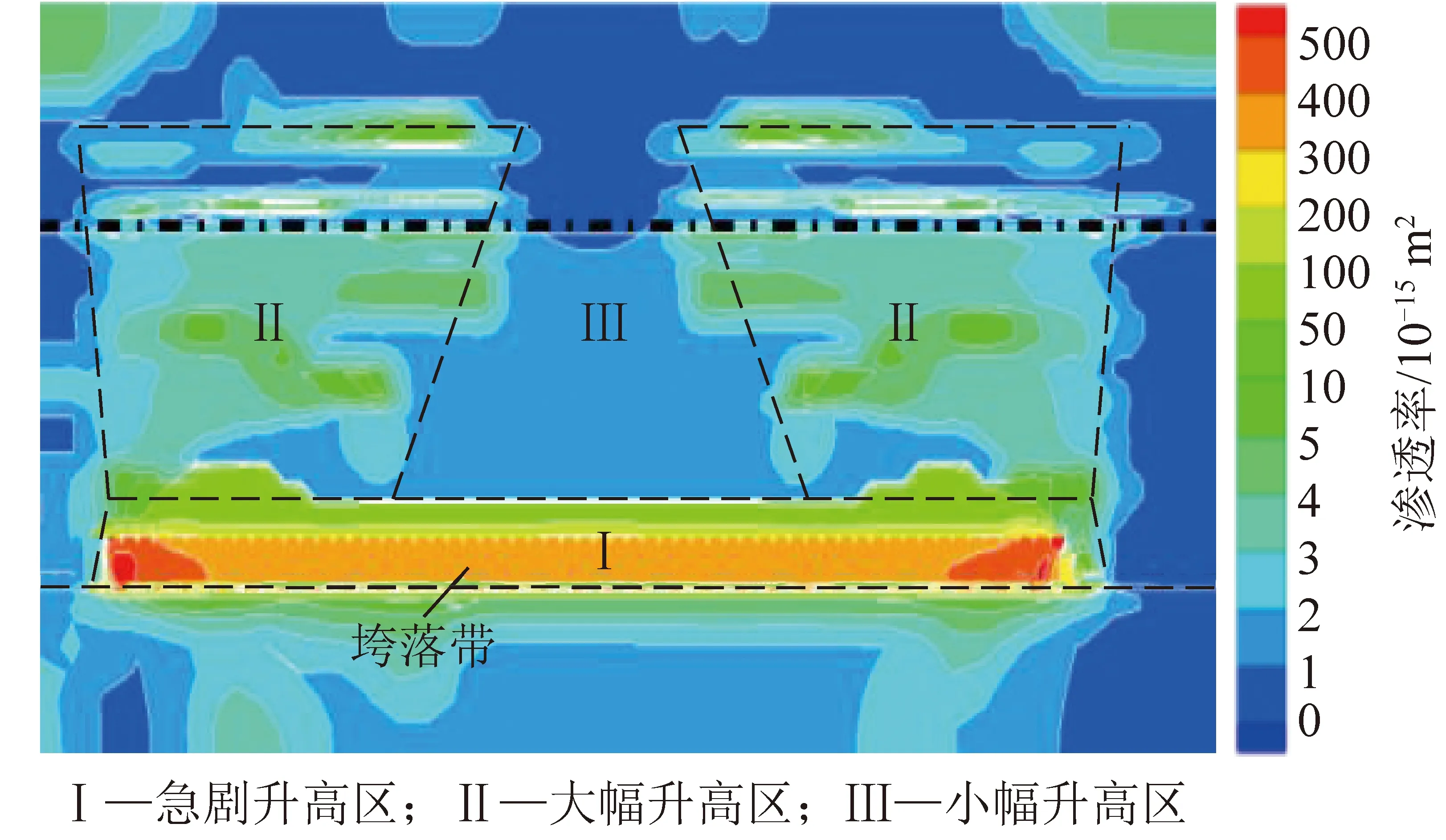
图2 采动覆岩渗透率分布云图[18]Fig.2 Permeability distribution of mining overburden[18]

对于研究区域内的某一岩层而言，不同位置渗透系数也不相同，因此首先需要对其自身进行等效渗透系数计算。同样的，假设岩层的垂向渗流也符合达西定律，并且厚度不变，仍为。同时设研究范围内岩层的总长度为(可由目标隔水层的移动边界角、目标隔水层距煤层顶板的距离及工作面的走向或推进长度确定，即=2cot+)，上下边界水头压差为Δ。将岩层沿长度方向划分为个变形微单元，每个变形微单元的长度为(∈[1，2，…，])，同时流经每个微变形单元的流量为(∈[1，2，…，])。单层岩层渗流示意如图3所示。

图3 单层岩层渗流示意Fig.3 Seepage diagram of single layer strata

单位宽度内垂直方向流过岩层的总流量为

(2)

又根据达西定律，单位宽度岩层内流经每个变形单元的水流流量为

(3)

因此对于岩层而言，单位宽度内垂直方向流过岩层的总流量为

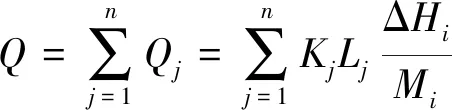
(4)

用一等效均质岩层来表示岩层，则可知流过该等效岩层的水流量也为，单位宽度内水流流过的横截面积同样为，设其等效渗透系数为eq。对该等效阻水岩层运用达西定律有

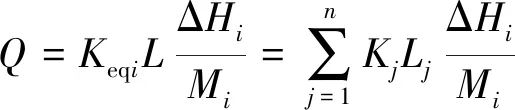
(5)

由式(5)可知，单一岩层的等效渗透系数为

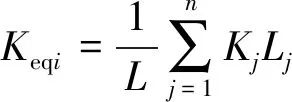
(6)

假设垮落带上部至目标隔水层之间的岩层总厚度=++1+…+；同时水流流经各岩层前后的水头压差为Δ，Δ+1，…，Δ，假设垮落带上方第1层岩层的底部为零水头位置，则研究区域内采动覆岩的总水头压差Δ=Δ+Δ+1+…+Δ。则采动覆岩整体等效渗透系数同样符合式(1)。结合上述得到的单一岩层的等效渗透系数计算式(6)，得到除垮落带外采动覆岩的整体等效渗透系数为

(7)

式中，为采动覆岩的整体等效渗透系数；为第层岩层内第块变形单元的渗透系数；为第层岩层内第块变形单元的长度。

由式(7)可知，采动覆岩等效渗透系数取决于研究区域内各岩层任一变形单元的长度和渗透系数。大量研究资料表明，岩石渗透率变化与体积应变之间存在函数关系。基于Kozeny-Caman方程，忽略岩石渗透率变化过程中热效应和单位体积内岩石颗粒表面积变化，同时结合岩石渗透系数与其渗透率之间的转换关系，得到岩石体积应变-渗透系数之间的函数关系为

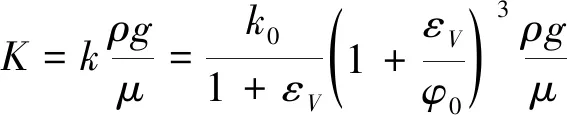
(8)

式中,为采动岩石渗透系数；为采动岩石渗透率；为岩石初始渗透率；为体积应变；为岩石初始孔隙率；为地下水的密度;为重力加速度;为地下水动力黏滞系数。

由式(8)可知，只要得到采动覆岩不同岩层不同变形单元的体积应变，即可计算该变形单元的采动渗透系数。取采动覆岩移动变形的主断面进行分析，式(8)可表达为

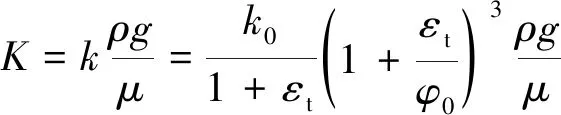
(9)

式中，为采动覆岩面应变。

另外，同时忽略覆岩面应变计算中的高阶小量，则有

(10)

式中，(,)为岩层水平移动量；(,)为岩层垂直下沉量。

对于采动覆岩各岩层的下沉值和水平移动值，可根据岩层移动影响函数法递推式进行计算(式(11))。

(11)

其中，(,)为第层岩层第个块体的水平移动量；(,)为第层岩层第个块体的垂直下沉量；为地表预计点(第层岩层第个块体)与地下开采单元点之间的水平距离；为第层岩体的下沉系数；为第层岩体受到采动影响的主要影响半径；为从煤层顶板到目标隔水层的岩层总层数；为工作面埋深；为覆岩主断面煤层采出长度(若沿工作面推进方向，为工作面连续推进长度；若沿工作面布置方向，为工作面面长)；1，2为覆岩主断面左右两侧岩层的拐点偏移距。另外，当=1时，取(′,-1)=(为煤层采高)，以保证计算的连续性。

联立式(7)，(9)～(11)，得到采动覆岩等效渗透系数的解析解表达式(12)。

由式(12)可知：对于某一矿井开采而言，根据矿井综合柱状图，在掌握垮落带上部第1层岩层至目标隔水层之间各岩层的厚度、覆岩岩层层数、岩层初始渗透率0、岩层初始孔隙率0、岩层下沉系数、拐点偏移距1，2(对于近水平煤层可认为1=2=)；主要影响半径、煤层埋深、煤层采出长度等参数条件下，根据式(12)即可得到某一采高条件下采动覆岩的等效渗透系数。

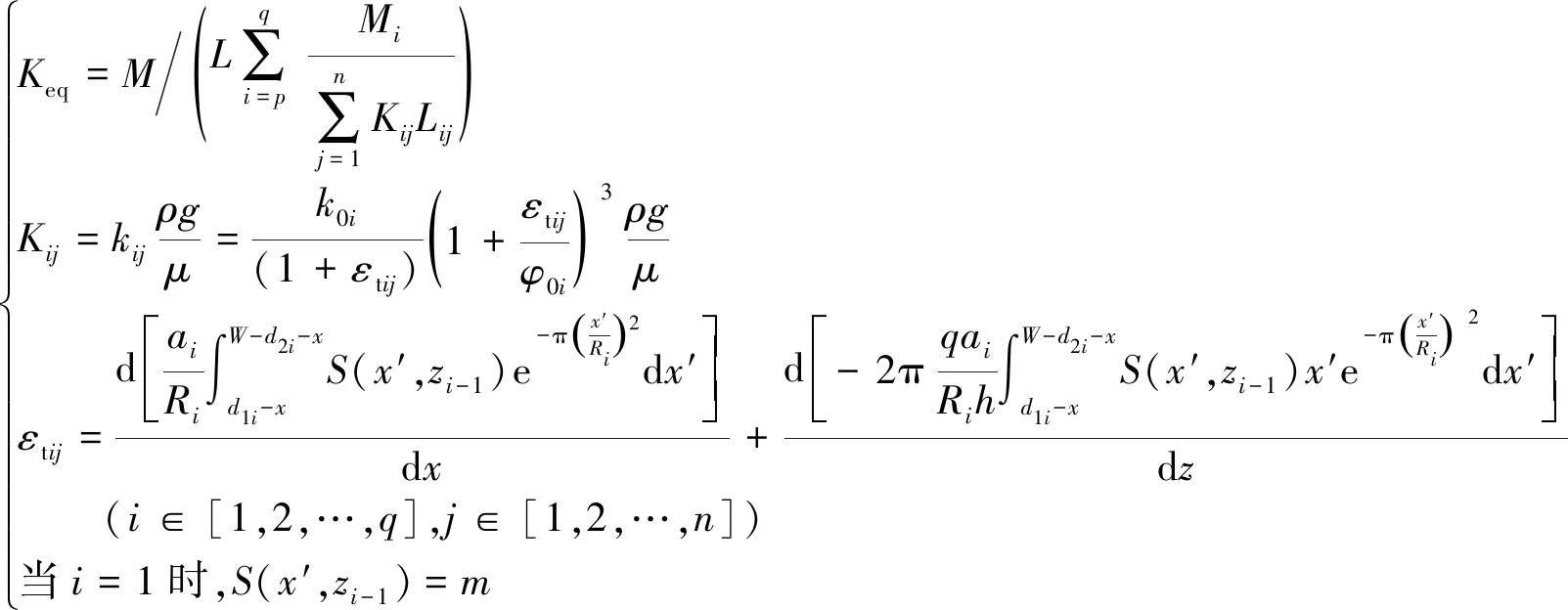
(12)

3 采动覆岩等效阻水厚度确定方法

为确定采动覆岩等效阻水厚度，假定采动覆岩垂向渗流速度与含水层补给速度相等为实现保水开采的临界条件。对于某一实际地层而言，当垮落带上方岩层至目标隔水层之间的岩层厚度、两端水头压差Δ、含水层水补给速度一定时(图4)，由式(13) 即能得到岩层厚度为条件下，能够实现保水采煤的最大临界渗透系数,即

==Δ

(13)

=Δ

(14)

图4 采动覆岩渗流变化Fig.4 Mining-induced overburden seepage variation

由式(13)可知，对于某一地层条件，假设覆岩两端初始水头压差Δ不变，采动覆岩渗透系数增大，相当于等效阻水厚度减小，认为采动覆岩的渗透系数与其等效阻水厚度成反比。以研究区域内岩层厚度为时所对应的最大临界渗透系数为参照，设采动覆岩等效渗透系数为时所对应的覆岩等效阻水厚度为，则有覆岩等效渗透系数与覆岩临界渗透系数的比值等于覆岩等效阻水厚度与岩层厚度之比的倒数，即

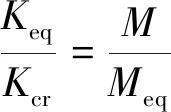
(15)

所以采动覆岩的等效阻水厚度为

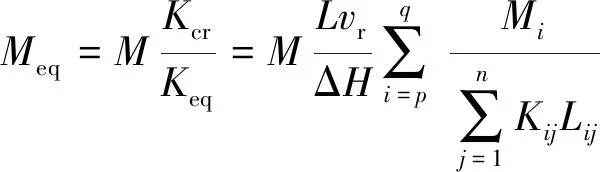
(16)

4 基于采动覆岩等效阻水厚度的保水采煤可行性判定方法

对于某一地层条件而言，煤层能否实现保水开采的本质在于采动覆岩的等效渗透系数是否超过维持含水层水位稳定所允许的最大临界渗透系数。因此煤层能够实现保水开采的判定条件为：≤，即≤1。根据式(15)可知，此时≥1，即采动覆岩的等效阻水厚度大于等于垮落带上方至目标隔水层之间的岩层厚度，这符合一般认知。

联立式(12)，(14)，(15)得煤层能够实现保水开采的判定条件为

(17)

5 工程案例分析

在得到覆岩等效阻水厚度及保水采煤预测方法的基础上，以新疆伊犁四矿21103工作面实际开采为例，对当前开采工艺参数条件下工作面保水开采可行性进行评价和预测。同时对工作面开采过程中含水层水位变化进行连续监测，以检验该预测方法的合理性和有效性。

5.1 工作面保水采煤可行性预测

伊犁四矿21103工作面钻孔综合柱状如图5所示。

图5 工作面综合柱状Fig.5 Comprehensive column of working face

工作面开采煤层为21-1煤，煤层厚度5 m，实际开采厚度=3.5 m，工作面长度=115 m。覆岩主要含水层为砾石层，含水层水位平均深度=10 m。由于伊犁四矿为典型的弱胶结地层，岩石强度为7.9～20.6 MPa，根据软弱岩层的垮落带高度经验公式，得到开采厚度=3.5 m时21103工作面的垮落带高度为

由此可知,21103工作面的垮落带高度的最大值为=8.02 m，发育高度为煤层直接顶泥岩层位，因此21103工作面垮落带高度上部至泥岩隔水层之间的总厚度=76.98 m。根据矿井的水文地质条件，伊犁四矿砾石含水层的水补给速度= 2.01 mm/d，采前各岩层的初始渗透系数见表1。以垮落带上边缘为0水头位置，则含水层水头高度Δ=+=86.98 m。此外，沿工作面布置方向，采动覆岩等效阻水厚度计算所需要的岩层移动相关参数见表2。

根据式(17)，通过Matlab编程得到采后覆岩各岩层的渗透率变化曲线，如图6所示。

表1 采前各岩层的初始渗透系数

表2 工作面岩层移动计算参数

图6 采后覆岩渗透率变化曲线Fig.6 Overburden permeability variation curves

根据式(6)计算得到研究区域内各单一岩层的等效渗透系数eq，见表3。

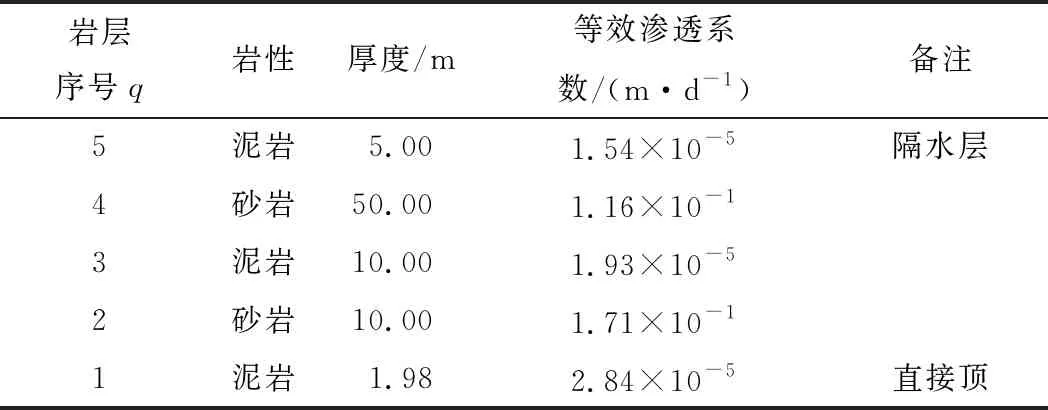
表3 单一岩层等效渗透系数计算结果

将表3计算结果代入式(7)，得到采动覆岩的整体等效渗透系数为

另外，当21103工作面垮落带高度上部至泥岩隔水层之间的总厚度=76.98 m时，结合含水层补给速度=2.01×10m/d，含水层水头高度Δ=86.98 m，得到21103工作面的最大临界渗透系数为

所以有

根据保水采煤可行性判定条件可以预测：在含水层水资源的补给作用下，新疆伊犁四矿21103工作面在开采厚度为3.5 m时能够实现保水采煤。

5.2 现场水位监测

为了检验上述理论计算结果的准确性和基于采动覆岩等效阻水厚度保水采煤可行性预测方法的可靠性，伊犁四矿21103工作面回采过程中，在工作面开切眼前方1 265 m处的运输平巷正上方，通过打设地面垂直水位观测孔(图7)，对工作面开采过程中砾石层水位变化进行连续监测，监测结果如图8所示。

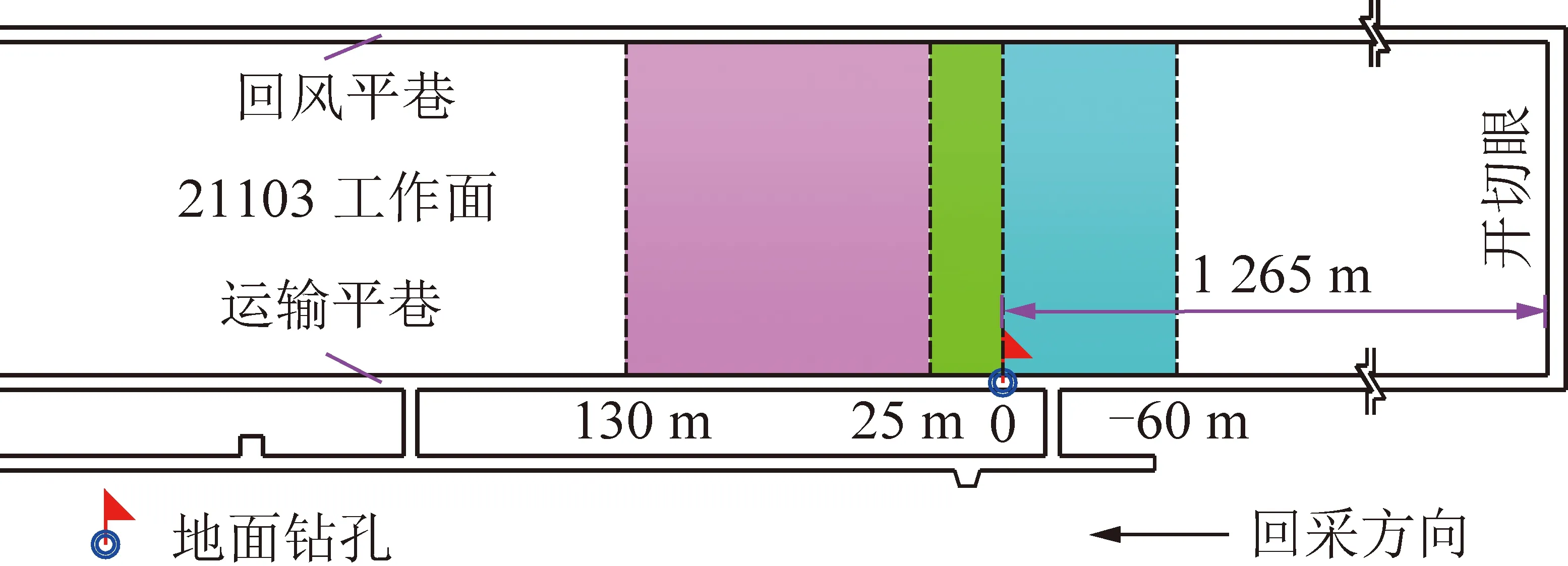
图7 地面垂直水位观测孔布置示意Fig.7 Layout of surface vertical borehole for water level observation

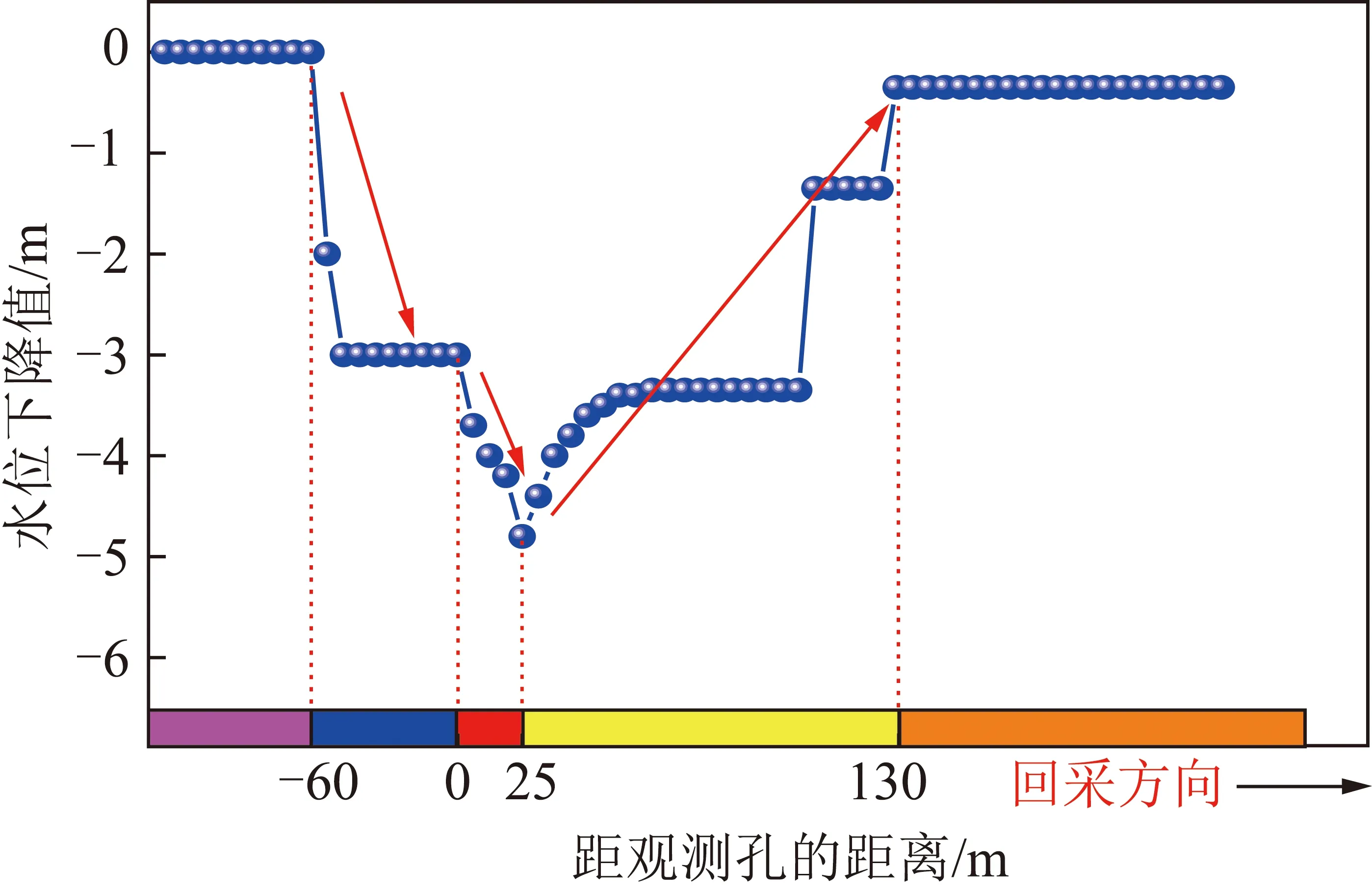
图8 观测孔水位变化Fig.8 Water level change in the borehole

由图8可知，当工作面距离观测孔60 m时，砾石含水层水位开始下降。这是由于受工作面回采影响，采空区上方覆岩形成下沉盆地，四周地下水流向下沉盆地中部进而造成含水层水位降低，该阶段水位下降-3 m；当工作面回采至观测孔下方时，覆岩垮落、变形、破坏，含水层水位进一步降低至最大下降值-4.8 m；当工作面推过观测孔25 m时，含水层水位开始回升；工作面推过130 m时，含水层水位回升至最大值-0.35 m，基本恢复至原水位水平。

现场水位观测结果表明：新疆伊犁四矿21103工作面正常回采达到了保水采煤的目的，说明上述对21103工作面保水采煤可行性理论预测结果是准确的，同时也表明基于覆岩等效阻水厚度保水采煤可行性预测方法的可靠性和有效性。

6 结 论

(1)从覆岩整体角度出发，考虑垮落带上方岩层至目标隔水层之间所有岩层在阻止含水层水资源流失方面的贡献，基于达西定律，得到了单一岩层在垂向渗流方向上的等效渗透系数eq计算式。在此基础上，推导出采动覆岩整体岩层在垂向渗流方向上的等效渗透系数数学表达式。

(2)基于Kozeny-Caman方程，得到了渗流过程中岩石体积应变-渗透系数函数关系。同时基于岩层下沉和水平移动的影响函数递推关系，结合地表移动变形计算参数，得到了采动覆岩移动变形主断面上任一变形单元体面应变的计算方法，进而得到采动覆岩等效渗透系数的解析解算法。

(3)以采后覆岩地下水渗流速度与含水层水资源补给速度相等为临界条件，得到岩层厚度为条件下采动覆岩能够实现保水采煤的最大临界渗透系数，进而得到采动覆岩等效阻水厚度计算方法。以采动覆岩等效渗透系数小于等于覆岩临界渗透系数为保水开采判定准则，得到矿井能够实现保水采煤的判定条件为：≥，即/≥1。

(4)将该预测方法应用到新疆伊犁四矿21103工作面保水采煤实践中，得到采动覆岩的等效阻水厚度与垮落带上方岩层至目标泥岩隔水层之间岩层厚度的比值为1.72，判定21103工作面以3.5 m采厚进行回采时能够实现保水采煤。现场水位监测结果检验了该预测结果的有效性。

[1] 张占斌. “十三五”国民经济和社会发展规划纲要亮点解析[J]. 环境保护，2016，44(5)：25-27.

ZHANG Zhanbin. The lightspot analysis of the 13th five-year plan for national economic and social development[J]. Environmental Protection，2016，44(5)：25-27.

[2] 范立民. 保水采煤面临的科学问题[J]. 煤炭学报，2019，44(3)：667-674.

FAN Limin. Some scientific issues in water-preserved coal mining[J]. Journal of China Coal Society，2019，44(3)：667-674.

[3] 张东升，李文平，来兴平，等. 我国西北煤炭开采中的水资源保护基础理论研究进展[J]. 煤炭学报，2017，42(1)：36-43.

ZHANG Dongsheng,LI Wenping，LAI Xingping et al. Development on basic theory of water protection during coal mining in northwest of China[J]. Journal of China Coal Society，2017，42(1)：36-43.

[4] FAN G，CHEN M，ZHANG D，et al. Experimental study on the permeability of weakly cemented rock under different stress states in triaxial compression tests[J]. Geofluids，2018，2018：1-9.

[5] ZHANG S，FAN G，ZHANG D，et al. Physical simulation research on evolution laws of clay aquifuge stability during slice mining[J]. Environmental Earth Sciences，2018，77(7)：1-10.

[6] 范钢伟，张世忠，张东升，等. 采动覆岩固液耦合物理模拟实验系统开发与应用[J]. 采矿与安全工程学报，2016，33(5)：898-903.

FAN Gangwei，ZHANG Shizhong，ZHANG Dongsheng，et al. Development and application of a solid-liquid coupling physical experiment system for modeling mining-induced overburden movement[J]. Journal of Mining & Safety Engineering，2016，33(5)：898-903.

[7] 高保彬，刘云鹏，潘家宇，等. 水体下采煤中导水裂隙带高度的探测与分析[J]. 岩石力学与工程学报，2014，33(S1)：3384-3390.

GAO Baobin，LIU Yunpeng，PAN Jiayu，et al. Delection and analysis of height of water flowing fractured zone in underwater mining[J]. Chinese Journal of Rock Mechanics and Engineering，2014，33(S1)：3384-3390.

[8] 范立民，马雄德，蒋泽泉，等. 保水采煤研究30年回顾与展望[J]. 煤炭科学技术，2019，47(7)：1-30.

FAN Limin,MA Xiongde,JIANG Zequan，et al. Review and thirty years prospect of research on water-preserved coal mining[J]. Coal Science and Technology，2019，47(7)：1-30.

[9] 刘世奇. 厚煤层开采覆岩破坏规律及粘土隔水层采动失稳机理研究[D]. 中国矿业大学(北京)，2016：97-111．

LIU Shiqi. The law of the overburden failure in thick coal seam mining and instability criterion of the clay aquiclude under the influence of mining[D]. Beijing:China University of Mining and Technology(Beijing)，2016：97-111．

[10] 马立强，余伊何，SPEARING A J S. 保水采煤方法及其适用性分区——以榆神矿区为例[J]. 采矿与安全工程学报，2019，36(6)：1079-1085.

MA Liqiang，YU Yihe，SPEARING A J S. Water conservation mining method and its applicability:A case study in Yushen mining area[J]. Journal of Mining & Safety Engineering，2019，36(6)：1079-1085.

[11] 徐智敏，孙亚军，高尚，等. 干旱矿区采动顶板导水裂隙的演化规律及保水采煤意义[J]. 煤炭学报，2019，44(3)：767-776.

XU Zhimin，SUN Yajun，GAO Shang，et al. Law of mining induced water conduction fissure in arid mining area and its significance in water-preserved coal mining[J]. Journal of China Coal Society，2019，44(3)：767-776.

[12] 许延春. 综放开采防水煤岩柱保护层的“有效隔水厚度”留设方法[J]. 煤炭学报，2005，30(3)：305-308.

XU Yanchun. Design methods of the effective water-resisting thickness for the protective seam of the water barrier in fully-caving mechanized coal mining[J]. Journal of China Coal Society，2005，30(3)：305-308.

[13] 李涛，王苏健，韩磊，等. 生态脆弱矿区松散含水层下采煤保护土层合理厚度[J]. 煤炭学报，2017，42(1)：98-105.

LI Tao，WANG Sujian，HAN Lei，et al. Reasonable thickness of protected loess under loose aquifer in ecologically fragile mining area[J]. Journal of China Coal Society，2017，42(1)：98-105.

[14] 黄庆享，蔚保宁，张文忠. 浅埋煤层黏土隔水层下行裂隙弥合研究[J]. 采矿与安全工程学报，2010，27(1)：35-39.

HUANG Qingxiang，WEI Baoning，ZHANG Wenzhong. Study of downward crack closing of clay aquiclude in shallowly buried coal seam[J]. Journal of Mining & Safety Engineering，2010，27(1)：35-39.

[15] 姚邦华，白海波，黄汉富，等. 采动覆岩隔水层稳定性力学模型及应用研究[J]. 采矿与安全工程学报，2012，29(3)：307-311.

YAO Banghua，BAI Haibo，HUANG Hanfu，et al. Mechanical model of stability of water-resistant strata under mining and its application[J]. Journal of Mining & Safety Engineering，2012，29(3)：307-311.

[16] 孙建，王连国，赵光明. 神东特殊保水开采煤层条带充填覆岩隔水层稳定性判据[J]. 中国矿业大学学报，2018，47(5)：957-968.

SUN Jian，WANG Lianguo，ZHAO Guangming. Stability criterion of overburden water-resistant strata supported by filling strip in Shendong special water-perserved mining area[J]. Journal of China University of Mining & Technology，2018，47(5)：957-968.

[17] FAN G，ZHANG D. Mechanisms of aquifer protection in underg-round coal mining[J]. Mine Water and the Environment，2015，34(1)：95-104.

[18] 张村. 高瓦斯煤层群应力-裂隙-渗流耦合作用机理及其对卸压抽采的影响[D]. 徐州：中国矿业大学，2017：135-138.

ZHANG Cun. Coupling mechanism of stress-fracture-flow in high gas coal seam group and its impact on pressure relief extraction[D]. Xuzhou：China University of Mining and Technology，2017：135-138.

[19] 李文平，李涛，尚荣. 陕北大型矿区煤炭开采覆岩结构变异及渗透性变化研究[A]. 第九届全国工程地质大会论文集[C]. 工程地质学报，2012：294-299.

LI Wenping，LI Tao，SHANG Rong. Study on the structure variation and permeability change of overlying stata after large coal mining in northern Shaanxi[A]. Proceedings of the 9th National Engineering Geology Congress[C]. Journal of Engineering Geology，2012：294-299.

[20] KHANAL M，GUO H，ADHIKARY D. 3D numerical study of underground coal mining induced strata deformation and subsequent permeability change[J]. Geotechnical and Geological Engineering，2019，37(1)：235-249.

[21] 王俊杰，陈亮，梁越. 地下水渗流力学[M]. 北京：中国水利水电出版社，2013.

[22] 许江，李波波，周婷，等. 加卸载条件下煤岩变形特性与渗透特征的试验研究[J]. 煤炭学报，2012，37(9)：1493-1498.

XU Jiang，LI Bobo，ZHOU Ting，et al. Experimental study of coal deformation and permeability characteristics under loading-unloading conditions[J]. Journal of China Coal Society，2012，37(9)：1493-1498.

[23] 龙俊西，孟英峰，李皋，等. 基于体积应变的储层渗透率计算新方法[J]. 油气藏评价与开发，2016，6(3)：19-22.

LONG Junxi，MENG Yingfeng，LI Gao，et al. A new calculation method for reservoir permeability based on volumetric strain[J]. Reservoir Evaluation and Development，2016，6(3)：19-22.

[24] 谢和平，张泽天，高峰，等. 不同开采方式下煤岩应力场-裂隙场-渗流场行为研究[J]. 煤炭学报，2016，41(10)：2405-2417.

XIE Heping，ZHANG Zetian，GAO Feng，et al. Stress-fracture-seepage field behavior of coal under different mining layouts[J]. Journal of China Coal Society，2016，41(10)：2405-2417.

[25] 季小凯，郭建斌，邢同菊，等. 煤系沉积岩应力-应变与应变-渗透率特征[J]. 煤田地质与勘探，2015，43(3)：66-71.

JI Xiaokai，GUO Jianbin，XING Tongju，et al. Characteristics of stress-strain and strain-permeability of coal-bearing sedimentary rocks[J]. Coal Geology & Exploration，2015，43(3)：66-71.

[26] 郭擎，鲜学福，周军平. 煤岩全应力应变过程体应变对渗透率的影响[J]. 地下空间与工程学报，2015，11(5)：1137-1143.

GUO Qing，XIAN Xuefu，ZHOU Junping. Effect of volumetric strain on permeability of coal in complete stress-strain process[J]. Chinese Journal of Underground Space and Engineering，2015，11(5)：1137-1143.

[27] 冉启全，李士伦. 流固祸合油藏数值模拟中物性参数动态模型研究[J]. 石油勘探与开发，1997，24(3)：61-65.

RAN Qiquan，LI Shilun. Study on dynamic model of physical parameters in numerical simulation of fluid-solid coupling reservoir[J]. Petroleum Exploration and Development，1997，24(3)：61-65.

[28] 李祥春，张良，赵艺良. 常规三轴压力下含瓦斯煤蠕变-渗流演化规律[J]. 工程科学与技术，2018，50(4)：55-62.

LI Xiangchun，ZHANG Liang，ZHAO Yiliang. Evolution of gas-filled coal creep-seepage under conventional triaxial compression[J]. Advanced Engineering Sciences，2018，50(4)：55-62.

[29] 陆卫东，程健维. 基于岩层移动计算的工作面覆岩体渗透率变化研究[J]. 采矿与安全工程学报，2018，35(1)：118-124.

LU Weidong，CHENG Jianwei. Study on the permeability change of overlying strata based on strata movement calculations[J]. Journal of Mining & Safety Engineering，2018，35(1)：118-124.