V2G模式下电动汽车有序充放电调度及其应用研究
刘志强,张谦,栗尧嘉,朱熠,胡悦
V2G模式下电动汽车有序充放电调度及其应用研究
刘志强,张谦,栗尧嘉,朱熠,胡悦
(输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆 400044)
随着电动汽车的发展,电动汽车大规模无序接入将给电网带来负荷峰谷差增大,配电网负荷局部过载,电网部分母线电压过低,线路损耗增大,配电网变压器容量越限等一系列问题。应用电动汽车与电网互动控制电动汽车的充放电过程,可有效缓解上述问题,并起到削峰填谷、平抑可再生能源间歇性和波动性的作用。从电动汽车集群充电需求和放电能力的时空分布、电动汽车与电网互动的充放电电价制定策略和电动汽车与电网互动分级调度模型三方面总结了电动汽车有序充放电调度及其应用的研究现状,并讨论了下一步的研究方向。
电动汽车与电网互动;时空分布;调度;频率调节;充放电电价
0 引言
随着环境污染和传统能源紧缺等问题日益凸显,具备节能和环保优势的电动汽车(electric vehicle, EV)是新能源汽车的主要发展方向。大力发展电动汽车是我国“节能减排”基本国策的要求之一[1]。近日,国务院办公厅发布了新能源汽车产业发展规划(2021-2035),以推动电动汽车及其相关技术在中国的使用和发展。
大规模的电动汽车无序接入,将给电力系统规划和运行带来负荷增长、峰谷差增大、电网运行优化控制难度增加等问题,对新型配电网规划提出新的要求。
应用电动汽车与电网互动技术(Vehicle-to-Grid, V2G)控制EV的充放电过程,可以缓解EV规模化发展对电力系统造成的负面影响,并起到削峰填谷、平抑可再生能源间歇性和波动性的作用[2]。同时,在电网发生故障时,电动汽车可以作为备用电源,为孤岛运行的配电网提供电能,起到提高配网的可靠性的作用。随着电池技术的迅速发展,电动汽车可调度容量越来越大。如何合理地调度电动汽车有序充放电以实现电网的优化运行,越来越受瞩目[3]。
本文将重点围绕V2G调度涉及的以下几方面研究工作开展讨论。
1) 电动汽车集群充电需求和放电能力的时空分布研究
电动汽车时空分布特点对V2G调度有着重要的影响。由于电动汽车具有移动特性,其可控容量不仅与时间有关系,也受到空间位置的影响,因此,需充分考虑电动汽车在路网上的随机性,对电动汽车整体充电需求和放电能力的时空分布进行研究,以获取电动汽车参与调度的可控容量大小。
2) 电动汽车与电网互动充放电电价制定策略
电动汽车作为一种居民日常交通工具,首先必须满足日常行驶要求。在满足行驶要求的前提下,经车主同意才能参与到电力系统调度当中。因此,制定合理的电价机制以激励车主参与V2G调度,对V2G的推广显得尤为重要[4]。
3) 电动汽车与电网互动分级调度模型研究
V2G调度逐渐由电网直接调度向分级调度转换,如图1所示。一级调度中心实现Aggregator与电网(aggregator-to-grid, A2G)之间的调度,二级调度中心实现电动汽车与Aggregator(Vehicle-to- Aggregator, V2A)之间的调度[5]。
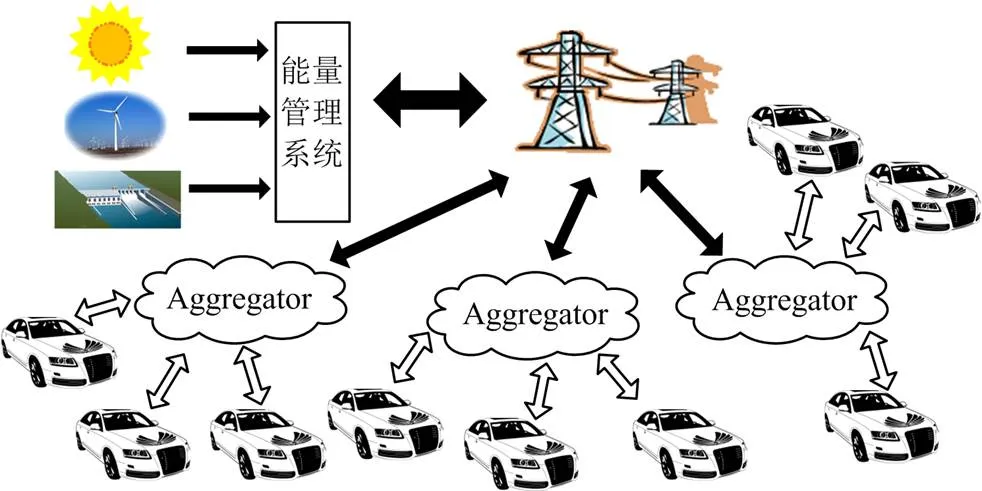
图1 电动汽车与电网互动分层调度示意图
大规模电动汽车的充放电调度计划是通过每一个电动汽车个体的充放电行为聚合后形成的群体策略,在制定电动汽车整体充放电策略时,需要进一步研究如何将该群体策略向下延伸分配至每个个体,并充分考虑个体的自身条件和意愿,体现充电策略的公平性和合理性。要实现电动汽车与电网互动的最优调度,不仅需研究A2G调度问题,同时需研究V2A调度问题。就目前而言,有关如何将区域电网层面的充电策略结果分解至每辆电动汽车上的研究相对较少。
本文将从上述三方面总结目前V2G调度及其应用研究相关工作,并讨论进一步的研究方向。
1 电动汽车充电需求和放电能力时空分布
随着电动汽车渗透率不断提升,未来大规模电动汽车接入电网,其充、放电行为给电网的稳定运行带来了挑战,精确预测电动汽车充电需求是研究电动汽车对电网双向互动的基础,对分析电动汽车接入电网的影响、电力系统规划及稳定运行具有重要意义。
1.1 电动汽车充电需求时空分布
目前对电动汽车充电负荷时空分布预测存在三个问题:第一,电动汽车空间行驶路径常规模拟方法,如最短路径算法、地块划分法与O-D反推法,都存在对驾驶者驾车随机性考虑不足的问题,并且电动汽车按照固定路线行驶,将导致相同起始点的电动汽车总是在固定的充电站充电;第二,考虑实时变化的交通状况以及驾驶者对路径随机选择的影响,采用动态交通流的方式进行模拟,但是现有方法为了追求模拟的准确性,通常需要建立多个非线性方程,进而产生巨大的计算量;第三,对电动汽车时空分布研究中常忽略交通拥堵状况与天气状况对电动汽车的能耗的影响,电动汽车在怠速与频繁启停和空调的开启都将导致能耗增高。
针对上述问题,文献[6]计及实时交通与温度,提出了一种基于马尔可夫决策过程随机路径模拟的城市电动汽车充电负荷时空分布预测方法,以计算出不同温度、不同交通状况下电动汽车充电负荷的时空分布。该方法能够避免最短路径算法中相同始终点电动汽车在固定地点充电的问题,体现电动汽车空间移动的随机性。算例仿真计算了电动汽车充电负荷时空分布,结果表明节点充电负荷具有明显峰谷差,并且承担快充能力越强的节点峰谷差越明显,交通枢纽节点负荷波动情况最严重;环境温度的升高对电动汽车能耗有着显著影响,导致节点充电负荷持续维持在高位;交通状况的恶化一方面会导致电动汽车充电负荷峰值增高,另一方面会导致峰值持续时间增长。
传统的蒙特卡洛方法不能及时更新每辆电动汽车的状态,而电动汽车接入电网的状态随时随地在发生改变,在电动汽车状态不变的情况下,传统方法可能产生大量的无效计算。为了提高算法效率,文献[7]提出了一种高效的准动态交通流模拟方法。基于静态交通流分布,利用出行链理论描述电动汽车车主的行驶习惯,同时在考虑交通拥堵对车主路径选择的影响下,利用改进后的蒙特卡洛法,计算了电动汽车的时空分布和实时荷电状态。仿真结果表明,该方法提高了传统蒙特卡洛法的计算速度;提高电动汽车的普及率、充电阈值和电池容量有利于配电网和电动汽车充电可靠性;降低放电阈值有利于提高配电网的可靠性,但不利于电动汽车充电的可靠性;当电动汽车数量较少或电池容量较低时,增加电动汽车数量和电池容量可以有效提高配电网和电动汽车充电可靠性。
文献[8]提出了改进的LSTM神经网络,预测精度更高、泛化能力更强。分析了天气因素、社会因素以及路网线路特性等因素对道路行车速度的影响,构建了基于平均速度预测的电动汽车能耗模型;提出考虑样本相似度的长短期记忆神经网络,对电动汽车平均速度进行了预测,计算了汽车行驶能耗,结合空调能耗得出单位里程电动汽车总耗电。
文献[9]考虑路况拥堵因素对电动汽车荷电量的影响,提出了一种基于聚类分析的电动汽车充电负荷预测方法,在分析常规充电负荷影响因素并初步建立概率分布模型的基础上,对每段行程的行驶里程和行驶时间构成的二维出行特征数据进行聚类分析。挖掘常规统计数据无法得到的道路拥堵因素,考虑不同路况条件下道路拥堵因素对电动汽车荷电状态的影响,并叠加该变量到负荷预测模型中,以实现电动汽车充电负荷的精确预测。
1.2 电动汽车可调度能量动态变化
在进行EV实时可控能量研究时,常简化各类型EV的交通属性、状态转换特性以及由于车辆使用的随机性,导致各时段参加调频的EV实时可控能量计算不准确。基于此,文献[10]分析了电动汽车的调度控制模式,综合考虑各类约束,设计了一种针对电动汽车实时可调度容量的具备普适性的评估算法,然后基于此方法计算出了分别适用于一次、二次和三次调频情景的电动汽车集群可调度容量。文献[11]根据用户出行需求和电池寿命约束,对电动汽车的可上调和可下调容量进行了评估,作为频率调节的依据。文献[12]在分析我国4种类型EV行驶规律的基础上,结合EV接入电网的状态转换特性,模拟计算EV可控数量和初始储能,其状态转换如图2所示。
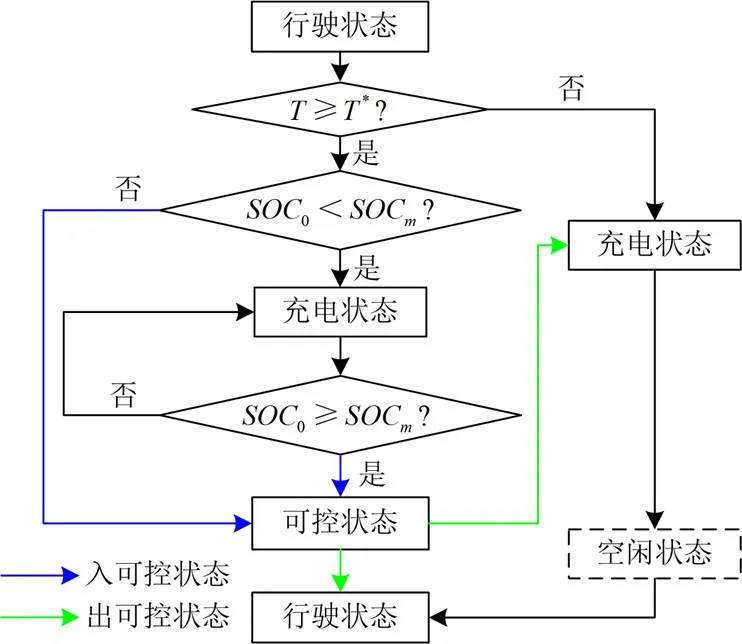
图2 EV的状态转换
在此基础上,文献[12]以计及电动汽车可控容量动态变化的负荷频率调整为目标,基于EV行驶规律计算出电动汽车的可控数量,进而计算出各类型电动汽车的实时可控能量。区域内EV实时可控能量动态模型如3所示。仿真结果表明:在相同电池总能量下,电动私家车在各类型EV中,参与系统调度的可控时段最多,实时可控能量最多。
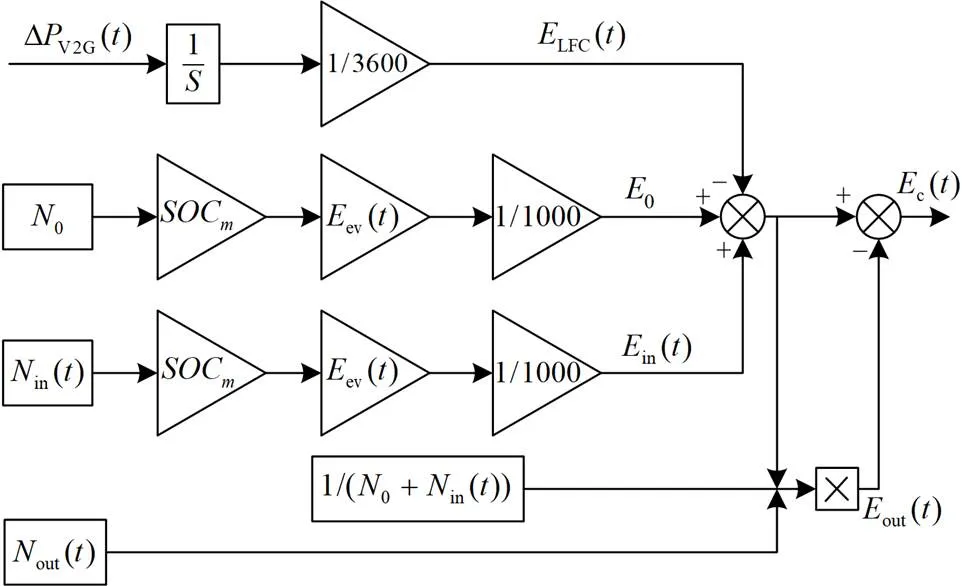
图3 EV实时可控能量动态模型
2 电动汽车与电网互动充放电电价制定策略
EV用户对电动汽车充放电行为的决策通常取决于实时电价的高低、日常出行需求等因素,因此可以通过充放电电价激励用户合理安排充放电时间,以实现电网负荷调整。而如何制定合理的EV充放电电价对数量庞大的电动汽车进行有效引导显得尤为重要。
2.1 电动汽车与电网互动的充电电价策略
目前制定的EV充电电价主要有静态峰谷电价[13-14]和动态分时电价[15-18]两类。文献[13]分析了电动汽车用户对电价变化的需求响应模型,提出能够影响电动汽车充放电行为的最优峰谷分时电价定价方案。2016年,深圳市率先出台电动汽车充电峰谷电价政策以引导用户在夜间低谷进行充电,其分时电价的费率不随电力系统实际运行情况动态调整[15]。然而静态峰谷电价仅能反映地区基础负荷情况,无法针对负荷激增或骤降等情景对充电电价进行适当调控,这可能导致系统负荷出现另一个高峰,从而影响配网安全运行。
针对静态峰谷电价可能给电网带来新的问题,国内外学者逐步开展电动汽车动态分时电价研究。文献[15]设计了一种EV充放电负荷与实时电价联动优化模型,以用户成本最小为目标实现电网经济调度。文献[16]提出基于动态分时电价的电动汽车有序充电控制方法,用户通过响应动态分时电价激励可显著降低充电站的运营成本和电动汽车用户的充电成本。文献[17]以EV充放电收益最大为目标,并在此基础上决策电动汽车充放电行为,仿真结果显示该模型能够体现用户对电价的响应能力,进一步说明对实时电价进行动态调整将更好地平滑网内负荷曲线。
但以上研究大多假设电动汽车严格遵守电网的调度命令,而忽略了电动汽车用户偏好与个人选择对整个系统调度结果的影响。为有效引导电动汽车进行有序充电行为,文献[18]充分考虑了电动汽车用户的个体行驶特性和自主选择性,建立了电动汽车并网场景和可控容量预测模型,设计了用于表征EV综合满意度的分项评价指标,并进一步提出计及用户满意度的电动汽车动态分时充电电价制定策略。仿真结果表明,所制定的动态分时充电电价能够引导EV用户转移充电负荷,在实现削峰填谷的同时,抑制负荷波动并提高了可再生能源的利用率。
2.2 电动汽车与电网互动的放电电价制定策略
目前关于EV参与备用电能市场交易的放电电价研究主要分为以下两种。
一是以电网运行效果或EV用户收益为目标优化EV充放电行为。文献[19]结合EV用户日常行驶需求、电池容量及充放电功率建立了EV参与电网调峰的模型,结果表明放电电价能够有效引导EV的放电行为。文献[20]兼顾EV成本和电网公司利益求解EV充放电电价的4个限值,以峰谷差最小及用户参与V2G成本最低为目标获得最优峰谷时段。文献[21]建立了计及多方利益的电动汽车有序充放电定价模型,并验证了不同电价下的满意度将影响EV用户的日常充放电习惯。
二是采用博弈的思想制定EV放电电价。文献[22]提出采用博弈论方法建立用户对期望电价与实际电价之间的差异满意度模型和双方效用函数,并使用反向归纳法获得纳什均衡解。文献[23]利用博弈论寻求电网和EV用户的纳什均衡,即合理的充放电电价,算例表明此电价能够有效激励EV参与V2G以降低峰荷。
文献[24]提出了一种基于模糊贝叶斯学习的电动汽车代理商与电力公司谈判报价模型,着重研究了电网与EV运营商的放电电价谈判过程,采用模糊贝叶斯学习以更新并修正估计值,通过谈判得到双方都可接受的放电电价。仿真结果表明,该策略为参与者增加了显著的经济效益,降低了电动汽车使用成本和电网运行成本。文献[25]基于合作博弈的思想,以电动汽车代理商与电动汽车用户的合作联盟收益最大为目标,建立了电动汽车的动态分时优化充放电模型,结果表明所提策略能有效减小峰谷差,同时提高了代理商和电动汽车用户的收益。
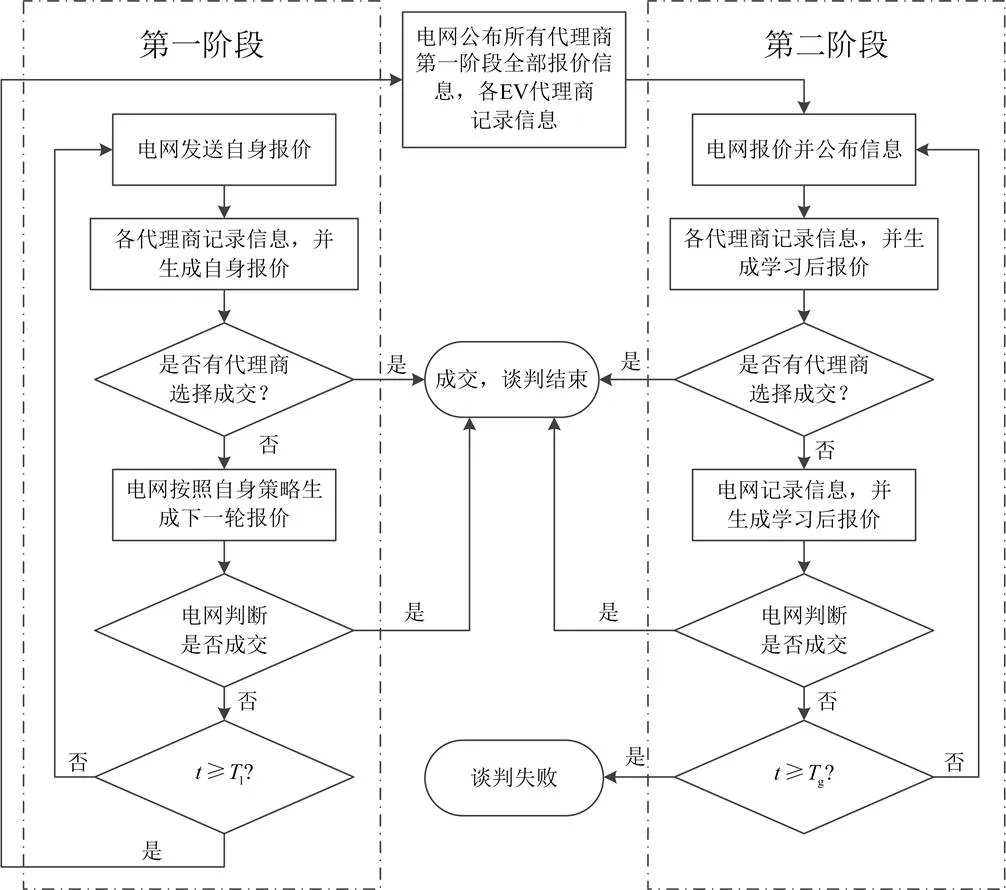
图4 一对多两阶段放电电价谈判流程图
针对一对一放电电价谈判模型未考虑多家电动汽车代理商参与谈判,竞争不足导致所得放电电价不合理的问题,文献[26-27]提出了在多代理情况下电动汽车参与优化调度的谈判策略,图4显示了一对多两阶段放电电价的具体谈判流程。仿真结果表明,使用一对多谈判模型得到的成交价格较为合理,也不会增加谈判轮数,同时增大了成交概率,因此,所制定的放电电价可激励电动汽车参与电力系统调度,达到缓解电网供电压力的目的。
3 电动汽车与电网互动分级调度模型
国内外对V2G调度问题的研究,通常是针对一级调度,且主要集中在以下两方面:计及V2G的机组组合研究和计及V2G的调频辅助服务研究。
3.1 计及V2G的机组组合
文献[28]构建了计及电动汽车充放电行为的机组组合模型,以实现系统的运行成本和碳排放成本最小,并进一步研究了风电、太阳能发电等新能源发电对调度的影响[29-30]。文献[31]将电动汽车换电站引入传统机组组合问题中,计及了换电站的充放电效率、电量平衡和满足日换电需求的最小储能等约束,提出换电站与电网互动的机组组合模型。
但上述研究仅给出电动汽车总体的充放电安排,尚未将控制分解到每辆电动汽车[32]。此外,目前的研究通常主观假定调度模型中V2G的可用容量为固定值,并能够满足调度需求[33]。且大多是以对电动汽车的直接调度为基本假设,认为调度人员在电动汽车申报可调度时段内可完全控制其充放电过程,未考虑电动汽车的随机性。

图5 电动汽车优先权调度方案
基于此,在文献[34]建立的一级调度模型基础上,计及电动汽车用户用车便利性,文献[35-36]建立了基于优先权的电动汽车集群充放电优化模型。通过分析电动汽车各项申报信息对代理商制定策略的影响,建立电动汽车评价指标体系,以电动汽车申报容量和时段、诚信度及电池损耗为评价指标,基于熵权法确定电动汽车调度优先权,从而得到电动汽车代理商所辖区域电动汽车集群充放电优化控制策略。电动汽车优先权调度方案如图5所示。
3.2 计及V2G的调频辅助服务
单辆电动汽车的电池容量及输出功率有限,故往往采取由聚合商统一管理电动汽车集群,再以电动汽车聚合商为单元提供调频服务的模式。文献[37]基于电动汽车的充放电静态频率特性模型,在电力系统负荷扰动发生时,实现了对电动汽车充放电的协调控制。但文中电动汽车与传统单元的调频需求功率分配比例固定,电动汽车的储能资源无法得到充分利用,调频效果不佳。文献[38]提出了基于电动汽车集群容量实时预测的负荷频率控制策略。该策略能够实时调整电动汽车集群的功率分配,既满足了电动汽车用户的行驶需求,又通过源荷互动提高了电网的频率稳定性,避免了由于调频功率分配不合理导致的调频效果不佳或资源浪费问题。
随着风力在电力系统中渗透率的增加,要求风力发电机具有控制有功输出的能力。为了弥补双馈感应发电机因风力发电的不确定性和波动性而在调频方面的不足,采用电动汽车作为辅助存储装置,辅助风力发电机参与系统的调频。文献[39]提出了一种双馈感应发电机和电动汽车集群的协同控制策略。在合理划分风速区域和选择桨距角运行点的基础上,提出了连续变化风速下双馈感应发电机备用容量的预测模型。考虑电动汽车车主需求,通过系统实时分配基于调频容量的调频任务,提出了双馈感应发电机与电动汽车集群的二次调频协调控制策略。
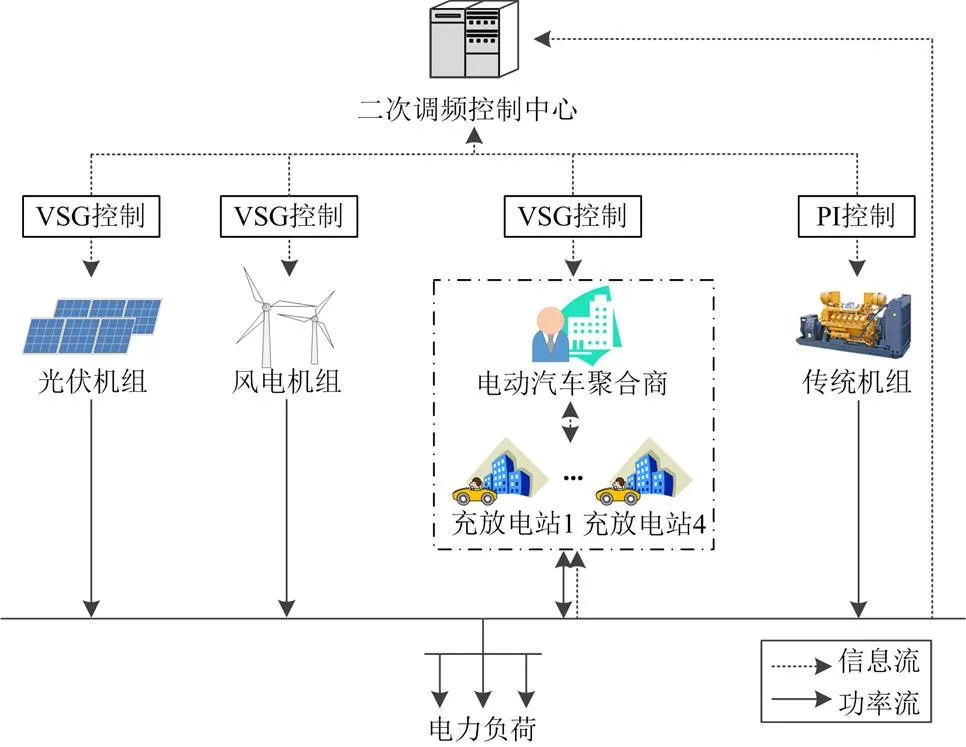
图6 系统调频控制模型
针对风电机组、光伏阵列和电动汽车集群微电网,文献[40]提出了一种基于虚拟同步发电机(VSG)的自适应二次调频策略。将改进的虚拟同步发电机控制方法应用于可再生能源发电机组和电动汽车集群,通过将比例积分控制引入虚拟同步发电机的频率控制器,实现无误差频率调节,结合风电机组、光伏阵列和电动汽车的实时调频备用容量,建立了虚拟同步发电机二次调频参数自适应调整策略。其系统调频控制模型如图6所示。
目前电动汽车调频研究一般考虑了满足车主的行驶需求或者最大化车主经济收益,但往往忽略了电动汽车在接受以调频为目的的调度之后,其需求充电负荷曲线因参与调频而发生改变,从而产生对电网侧造成不利影响的可能。
文献[41]提出了计及车主行驶需求的电动汽车集群调频控制策略,设定电动汽车均在临近出发时退出调频,然后充电至需求电量后立刻开始行驶。文献[42]中的自主调频控制方案也设定在接近车主预设的离网时刻时切换至智能充电模式,为满足出行计划而进行充电。然而,由于同类型车辆的行驶规律相似,会出现大量电动汽车聚集在相近时段进行充电的情况,从而造成电网峰谷差加大。在文献[43]的研究中,进行单辆电动汽车的调频调用时,实时调整预定的V2G功率以补偿由不确定性调度导致的电池电量变化,以保证离网时达到车主预期的荷电状态。但是这种方法仅对充电功率进行调整,并未对充电时段进行安排设计,因此无法避免出现集中性的充电负荷高峰。文献[44]提出了电动汽车参与调频的多目标优化控制策略,可以实现最小化电网频率偏差,按容量比例分配调频信号,最大程度支持双向V2G,以及避免频繁充放电造成电池退化,但并未将抑制充电负荷对电网的负面影响纳入优化目标。
同时,针对电动汽车集群参与调频时的调度管理大多采用传统的集中式控制结构。文献[45]设计了基于自适应动态规划的电动汽车聚合商调频控制器,在稳定智能电网频率方面表现出优越的性能,其中聚合商以集中式控制方式对单辆电动汽车进行调度。文献[46]建立了包含多个电动汽车聚合商的考虑时变时延的负荷频率控制模型,其中控制中心对各聚合商、聚合商对所管理的电动汽车均采用集中式控制。然而,对于包含大量车辆的电动汽车集群而言,集中式控制结构处理调频相关信息时的计算量过大,对中心控制节点的要求极高,并且可靠性较低,一旦出现通信故障将严重影响调频性能。因此,文献[47]提出了考虑实际限制的风电机组和电动汽车协同调频策略,并对比了集中式和分布式控制结构对调频的影响,证明分布式控制可以减小时间延迟,且不需要在通信网络上耗费过高成本。
更进一步地,文献[48]建立了电动汽车分层分布式控制框架并引入负荷需求优化,大幅度减轻了电动汽车退出调频后的无序充电现象。仿真结果表明,所提出的计及需求充电负荷优化的电动汽车集群分层分布式调频策略,不仅能自适应调整以保证预期的调频效果,还能降低电网侧的供电压力,实现电动汽车集群高效可靠的调度。
4 结论
本文主要从电动汽车的时空分布、充放电价策略和电动汽车与电网互动的分级调度模型等方面,总结了目前V2G调度及其应用研究相关工作,随着电动汽车有序充放电调度的推广应用,拟从以下两方面开展进一步研究:
1) “车-路-网”耦合下,充分考虑电动汽车移动特性,结合电动汽车准确时空分布和充电站对用户吸引度,开展电动汽车充电站选址定容研究。
2) 基于区块链技术,开展电动汽车能源交易策略与模型、充电运营商之间的利润博弈策略及电动汽车充电引导优化研究。
[1] 陈凯炎, 牛玉刚. 基于V2G技术的电动汽车实时调度策略[J]. 电力系统保护与控制, 2019, 47(14): 1-9.
CHEN Kaiyan, NIU Yugang. Real-time scheduling strategy of electric vehicle based on vehicle-to-grid application[ J]. Power System Protection and Control, 2019, 47(14): 1-9.
[2] 彭晶, 黄虹, 刘福潮, 等. 基于V2G技术的电动汽车有序充放电策略研究[J]. 电气自动化, 2020, 42(5): 12-15.
PENG Jing, HUANG Hong, LIU Fuchao, et al. Research on PHEV orderly charge/discharge strategy based on V2G technology[J]. Electrical Automation, 2020, 42(5): 12-15.
[3] 于会群, 尹申, 张浩, 等. 考虑电动汽车用户满意度的微网分层优化调度策略[J]. 中国电力, 2020, 53(12): 83-91.
YU Huiqun, YIN Shen, ZHANG Hao, et al. Optimization strategy of microgrid hierarchical scheduling considering electric vehicles user satisfaction degree[J]. Electric Power, 2020, 53(12): 83-91.
[4] 谭维玉, 雷雨, 李军, 等. 计及动态分时电价的电动汽车参与电网调度研究[J]. 可再生能源, 2020, 38(11): 1515-1522.
TAN Weiyu, LEI Yu, LI Jun, et al. Research on the participation of electric vehicles in power system dispatching considering dynamic time-of-use price[J]. Renewable Energy Resources, 2020, 38(11): 1515-1522.
[5] 卢少平, 应黎明, 王霞, 等. 基于用户出行模拟的电动汽车快充站负荷预测及其优化调度[J]. 电力建设, 2020, 41(11): 38-48.
LU Shaoping, YING Liming, WANG Xia, et al. Charging load prediction and optimized scheduling of electric vehicle quick charging station according to user travel simulation[J]. Electric Power Construction, 2020, 41(11): 38-48.
[6] 张谦, 王众, 谭维玉, 等. 基于MDP随机路径模拟的电动汽车充电负荷时空分布预测[J]. 电力系统自动化, 2018, 42(20): 59-66.
ZHANG Qian, WANG Zhong, SU Yaojia, et al. Spatial- temporal distribution prediction of charging load for electric vehicle based on MDP random path simulation[J]. Automation of Electric Power Systems, 2018, 42(20): 59-66.
[7] ZHANG Qian, ZHU Yi, WANG Zhong, et al. Reliability assessment of distribution network and electric vehicle considering quasi-dynamic traffic flow and vehicle-to- grid[J]. IEEE Access, 2019, 7: 131201-131213.
[8] 程江洲, 余子容, 程杉, 等. 城市路网中考虑多方影响的电动汽车能耗预测[J]. 电测与仪表, 2020, 57(20): 90-97.
CHENG Jiangzhou, YU Zirong, CHENG Shan, et al. Energy consumption prediction of electric vehicle considering multiple influences in urban road network[J]. Electrical Measurement & Instrumentation, 2020, 57(20): 90-97.
[9] 王睿, 高欣, 李军良, 等. 基于聚类分析的电动汽车充电负荷预测方法[J]. 电力系统保护与控制, 2020, 48(16): 37-44.
WANG Rui, GAO Xin, LI Junliang, et al. Electric vehicle charging demand forecasting method based on clustering analysis[J]. Power System Protection and Control, 2020, 48(16): 37-44.
[10]张聪, 张祥文, 夏俊荣, 等. 电动汽车实时可调度容量评估方法研究[J]. 电力系统保护与控制, 2015, 43(22): 99-106.
ZHANG Cong, ZHANG Xiangwen, XIA Junrong, et al. Research on estimation of electric vehicles real-time schedulable capacity[J]. Power System Protection and Control, 2015, 43(22): 99-106.
[11]何晨颖, 耿天翔, 许晓慧, 等. 利用电动汽车可调度容量辅助电网调频研究[J]. 电力系统保护与控制, 2015, 43(22): 134-140.
HE Chenying, GENG Tianxiang, XU Xiaohui, et al. Research on grid frequency regulation using schedulable capacity of electric vehicles[J]. Power System Protection and Control, 2015, 43(22): 134-140.
[12]张谦, 李晨, 周林, 等. 计及电动汽车实时可控能量动态变化的负荷频率控制[J]. 电力自动化设备, 2017, 37(8): 234-241.
ZHANG Qian, LI Chen, ZHOU Lin, et al. Load frequency control considering dynamic change of real-time controllable EV energy[J]. Electric Power Automation Equipment, 2017, 37(8): 234-241.
[13] 高亚静, 王辰, 吕孟扩, 等. 计及车主满意度的电动汽车最优峰谷分时电价模型[J]. 电力自动化设备, 2014, 34(2): 8-13.
GAO Yajing, WANG Chen, LÜ Mengkuo, et al. Optimal time-of-use price model considering satisfaction degree of electric vehicle owners[J]. Electric Power Automation Equipment, 2014, 34(2): 8-13.
[14]深圳市发展和改革委员会关于明晰电动汽车充电设施居民合表用户电价政策的通知[EB/OL]. [2016-12-23]. http://www.szpb.gov.cn/fgzl/jgzc/jggl3/201707/t20170720_7909230.htm.
[15]麻秀范, 王超, 洪潇, 等. 基于实时电价的电动汽车充放电优化策略和经济调度模型[J]. 电工技术学报, 2016, 31(1): 190-202.
MA Xiufan, WANG Chao, HONG Xiao, et al. Optimal scheduling of charging and discharging of electric vehicle based on real time price and economic dispatch model[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 190-202.
[16]徐智威, 胡泽春, 宋永华, 等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22): 3638-3646.
XU Zhiwei, HU Zechun, SONG Yonghua, et al. Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J]. Proceedings of the CSEE, 2014, 34(22): 3638-3646.
[17] 李明洋, 邹斌. 电动汽车充放电决策模型及电价的影响分析[J]. 电力系统自动化, 2015, 39(15): 75-81.
LI Mingyang, ZOU Bin. Charging and discharging decision-making model of electric vehicles and influence analysis of electricity price[J]. Automation of Electric Power Systems, 2015, 39(15): 75-81.
[18] ZHANG Qian, HU Yue, TAN Weiyu, et al. Dynamic time-of-use pricing strategy for electric vehicle charging considering user satisfaction degree[J]. Applied Sciences- basel, 2020, 10(9): 3247.
[19]吴浩. 电动汽车与电网互动技术的研究[D]. 天津: 天津理工大学, 2014.
WU Hao. Research on electric vehicle to interact with the grid technology[D]. Tianjin: Tianjin University of Technology, 2014.
[20]闫志杰, 张蕊萍, 董海鹰, 等. 基于需求响应的电动汽车充放电电价与时段研究[J]. 电力系统保护与控制, 2018, 46(15): 16-22.
YAN Zhijie, ZHANG Ruiping, DONG Haiying, et al. Price and period research of electric vehicles charging and discharging based on demand response[J]. Power System Protection and Control, 2018, 46(15): 16-22.
[21]崔金栋, 罗文达, 周念成. 基于多视角的电动汽车有序充放电定价模型与策略研究[J]. 中国电机工程学报, 2018, 38(15): 4438-4450.
CUI Jindong, LUO Wenda, ZHOU Niancheng. Research on pricing model and strategy of electric vehicle charging and discharging based on multi view[J]. Proceedings of the CSEE, 2018, 38(15): 4438-4450.
[22] YANG P, TANG G, NEHORAI A. A game-theoretic approach for optimal time-of-use electricity pricing[J]. IEEE Transactions on Power Systems, 2013, 28(2): 884-892.
[23] ZHENG S, XIANG Y, SHI L, et al. A cooperative game-based negotiation strategy of electric vehicle discharging price[C] // 2019 IEEE Sustainable Power and Energy Conference (iSPEC), November 21-23, 2019, Beijing, China: 2437-2442.
[24]张谦, 蔡家佳, 李春燕, 等. 基于模糊贝叶斯学习的电动汽车放电电价谈判策略[J]. 中国电机工程学报, 2018, 38(1): 61-71.
ZHANG Qian, CAI Jiajia, LI Chunyan, et al. The negotiation strategy of discharging price of electric vehicle based on fuzzy bayesian learning[J]. Proceedings of the CSEE, 2018, 38(1): 61-71.
[25]程杉, 陈梓铭, 徐康仪, 等. 基于合作博弈与动态分时电价的电动汽车有序充放电方法[J]. 电力系统保护与控制, 2020, 48(21): 15-21.
CHENG Shan, CHEN Ziming, XU Kangyi, et al. An orderly charging and discharging method for electric vehicles based on a cooperative game and dynamic time-of-use price[J]. Power System Protection and Control, 2020, 48(21): 15-21.
[26] 张谦, 丁铸玮, 谭维玉, 等. 计及多代理的电动汽车放电电价两阶段谈判策略[J]. 电工技术学报, 2018, 33(增刊2): 616-628
ZHANG Qian, DING Zhuwei, TAN Weiyu, et al. A two-stage negotiation strategy of discharging price for electric vehicle considering multi-agent[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 616-628.
[27] ZHANG Qian, DING Zhuwei, TAN Weiyu, et al. Negotiation strategy of discharging price between power grid and electric vehicles considering multi-agent[J]. IET Generation, Transmission & Distribution, 2020, 14(5): 833-844.
[28] SABER A Y, VENAYAGAMOORTHY G K. Intelligent unit commitment with vehicle-to-grid—a cost emission optimization[J]. Journal of Power Sources, 2010, 195(3): 898-911.
[29] SABER A Y, VENAYAGAMOORTHY G K. Plug-in vehicles and renewable energy sources for cost and emission reductions[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1229-1238.
[30] SABER A Y, VENAYAGAMOORTHY G K. Resource scheduling under uncertainty in a smart grid with renewables and plug-in vehicles[J]. IEEE Systems Journal, 2012, 6(1): 103-109.
[31] 张舒, 胡泽春, 宋永华, 等. 考虑电动汽车换电站与电网互动的机组组合问题研究[J]. 中国电机工程学报, 2012, 32(10): 49-55.
ZHANG Shu, HU Zechun, SONG Yonghua, et al. Research on unit commitment considering interaction between battery swapping station and power grid[J]. Proceedings of the CSEE, 2012, 32(10): 49-55.
[32] 王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述[J]. 中国电机工程学报, 2013, 33(1): 1-10.
WANG Xifan, SHAO Chengcheng, WANG Xiuli, et al. Survey of electric vehicle charging load and dispatch control strategies[J]. Proceedings of the CSEE, 2013, 33(1): 1-10.
[33]刘文霞, 赵天阳, 邱威, 等. 规模化EV充电与风力/火电发电系统协调运行[J]. 电工技术学报, 2013, 28(5): 49-57.
LIU Wenxia, ZHAO Tianyang, QIU Wei, et al. Coordinated operation of large scale electric vehicles charging with wind-thermal power system[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 49-57.
[34]张谦, 刘超, 周林, 等. 计及可入网电动汽车最优时空分布的双层经济调度模型[J]. 电力系统自动化, 2014, 38(20): 40-45.
ZHANG Qian, LIU Chao, ZHOU Lin, et al. A bi-level economy dispatch model considering temporal and spatial optimal distribution of electric vehicles[J]. Automation of Electric Power Systems, 2014, 38(20): 40-45.
[35]张谦, 蔡家佳, 刘超, 等. 基于优先权的电动汽车集群充放电优化控制策略[J]. 电工技术学报, 2015, 30(17): 117-125.
ZHANG Qian, CAI Jiajia, LIU Chao, et al. Optimal control strategy based on the priority of cluster charging and discharging of electric vehicles[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 117-125
[36] ZHANG Qian, LIU Huazhen, LI Chen. A hierarchical dispatch model for optimizing real-time charging and discharging strategy of electric vehicles[J]. IEEJ Transactions on Electrical and Electronic Engineering. 2018, 13(4): 537-548.
[37]张谦, 周林, 周雒维, 等. 计及电动汽车充放电静态频率特性的负荷频率控制[J]. 电力系统自动化, 2014, 38(16): 74-80.
ZHANG Qian, ZHOU Lin, ZHOU Luowei, et al. Load frequency control considering charging and discharging static frequency characteristics of electric vehicles[J]. Automation of Electric Power Systems, 2014, 38(16): 74-80.
[38] ZHANG Qian, LI Yan, LI Chen, et al. Real-time adjustment of load frequency control based on controllable energy of electric vehicles[J]. Transactions of the Institute of Measurement and Control, 2020, 42(1): 42-54.
[39] ZHANG Qian, LI Yan, LI Chen, et al. Coordinated secondary frequency regulation strategy of doubly-fed induction generator and electric vehicle[J]. Applied Sciences-basel, 2019, 9(14): 2815
[40] ZHANG Qian, LI Yan, DING Zhuwei, et al. Self-adaptive secondary frequency regulation strategy of micro-grid with multiple virtual synchronous generators[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 6007-6018.
[41] ZHANG Qian, LI Yan, LI Cheng, et al. Grid frequency regulation strategy considering individual driving demand of electric vehicle[J]. Electric Power Systems Research, 2018, 163: 38-48.
[42] OTA Y, TANIGUCHI H, BABA J, et al. Implementation of autonomous distributed V2G to electric vehicle and DC charging system[J]. Electric Power Systems Research, 2015, 120: 177-183.
[43] LIU H, QI J, WANG J, et al. EV dispatch control for supplementary frequency regulation considering the expectation of EV owners[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3763-3772.
[44] KAUR K, SINGH M, KUMAR N. Multiobjective optimization for frequency support using electric vehicles: an aggregator-based hierarchical control mechanism[J]. IEEE Systems Journal, 2019, 13(1): 771-782.
[45] MU C, LIU W, XU W. Hierarchically adaptive frequency control for an EV-integrated smart grid with renewable energy[J]. IEEE Transactions on Industrial Informatics, 2018, 14(9): 4254-4263.
[46] KO K S, SUNG D K. The effect of ev aggregators with time-varying delays on the stability of a load frequency control system[J]. IEEE Transactions on Power Systems, 2018, 33(1): 669-680.
[47] ARANI M F M, MOHAMED Y A I. Cooperative control of wind power generator and electric vehicles for microgrid primary frequency regulation[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5677-5686.
[48] DENG Xiaosong, ZHANG Qian, LI Yan, et al. Hierarchical distributed frequency regulation strategy of electric vehicle cluster considering demand charging load optimization[C] // 2020 IEEE Student Conference on Electric Machines and Systems (SCEMS), December 4-6, 2020, Jinan, China.
Research on orderly charging and discharging scheduling and application of electric vehicle based on vehicle-to-grid
LIU Zhiqiang, ZHANG Qian, SU Yaojia, ZHU Yi, HU Yue
(State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China)
With the development of electric vehicles, large-scale disordered access of electric vehicles will bring a series of problems to the grid, such as the further increase of peak-valley difference of load, local overload of load in power network, low bus voltage in some parts of the power network, increasing of line loss and the out of limit capacity of transformer in the distribution network. The application of vehicle-to-grid technology to control the charging and discharging process of electric vehicles can effectively alleviate the above problems. What’s more, it can reduce the peak, fill the valley and suppress the intermittency and volatility of renewable energy. This paper summarizes the research condition of electric vehicles orderly charging and discharging scheduling and application from three aspects: the spatial-temporal distribution of electric vehicles’ cluster charging demand and discharge capacity; the charging and discharging price strategy of electric vehicles interacting with the grid; the hierarchical scheduling model of electric vehicles interacting with the grid. In the end, this paper discusses the future research direction.
vehicle-to-grid; spatial-temporal distribution; scheduling; frequency regulation; charging and discharging price
2022-08-11;
2022-10-15
刘志强(1998—),男,硕士研究生,研究方向为电动汽车与电网互动技术、电力系统频率调节;E-mail: 1119597419@qq.com
张 谦(1980—),女,通信作者,博士,副教授,研究方向为电动汽车与电网互动、电力市场、新能源消纳;E-mail: zhangqian@cqu.edu.cn
栗尧嘉(1996—),男,硕士研究生,研究方向为电动汽车与电网互动技术。E-mail: 1306765948@qq.com

