Iterative filtered ghost imaging

Shao-Ying Meng(孟少英) Mei-Yi Chen(陈美伊) Jie Ji(季杰) Wei-Wei Shi(史伟伟)Qiang Fu(付强) Qian-Qian Bao(鲍倩倩) Xi-Hao Chen(陈希浩) and Ling-An Wu(吴令安)

1Key Laboratory of Optoelectronic Devices and Detection Technology,School of Physics,Liaoning University,Shenyang 110036,China

2Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

It is generally believed that,in ghost imaging,there has to be a compromise between resolution and visibility. Here we propose and demonstrate an iterative filtered ghost imaging scheme whereby a super-resolution image of a grayscale object is achieved, while at the same time the signal-to-noise ratio (SNR) and visibility are greatly improved, without adding complexity. The dependence of the SNR,visibility,and resolution on the number of iterations is also investigated and discussed. Moreover,with the use of compressed sensing the sampling number can be reduced to less than 1%of the Nyquist limit, while maintaining image quality with a resolution that can exceed the Rayleigh diffraction bound by more than a factor of 10.

Keywords: ghost imaging,bandpass filtering,compressed sensing,iteration

1. Introduction

Ghost imaging(GI)[1–8]is a recent newly-developed technique which can recover the spatial information of an object via the correlation measurement of two beams, neither of which can image the object independently. This powerful technology enables a high-quality image to be obtained even in a harsh environment such as a scattering medium[9]and turbulent atmosphere;[10]it has many promising applications in microscopy,[11]remote sensing,[12]optical encryption,[13]and various other fields. Although thermal GI had some drawbacks of low visibility, low signal-to-noise ratio (SNR) and long acquisition time in the original approach, after almost twenty years of development these problems may now be resolved through various methods, such as high-order GI,[14]differential GI,[15]computational GI,[16,17]correspondence imaging,[18]and compressed GI.[19]Meanwhile,its ability to reconstruct a high resolution image exceeding the Rayleigh diffraction limit has been verified by many groups.[20–27]

Resolution,visibility and SNR are the three most important parameters that characterize the quality of an image. In particular,much research has concentrated on how to increase the SNR.In 2014,an iterative GI scheme[28]was demonstrated that can greatly enhance both SNR and resolution based on computational GI. Shortly thereafter Yaoet al. presented a new technique to denoise the traditional ghost image by iterative GI algorithms.[29]A few years later, motivated by the first application of deep learning in optical imaging,[30]a novel deep learning method was introduced to improve the image quality in GI,with an extremely low sampling rate.[31,32]Recently, another new approach for recovering super-resolution ghost images of objects in a lensless filtered GI(FGI)system was demonstrated,[26,27,33]where the spatial resolution can greatly exceed the Rayleigh diffraction bound by more than a factor of 10.[33]However, the latter papers mainly focused on the improvement of imaging resolution and left the issues of SNR and visibility untouched,so these require further consideration. Previously, the general view was that one had to compromise between resolution and visibility,[4]but with our scheme we can overcome this difficulty.

2. Theory and method

In this letter,we propose an iterative FGI method to realize a ghost image of a grayscale object,performed by iteration of the filtered intensities of different thresholds and their correlations in the FGI equation for a given sample number(see Eqs. (3) and (4) below). The imaging quality is then evaluated through inspection of the three most important parameters mentioned above. It is somewhat surprising that high resolution can be achieved,while the SNR and visibility are greatly improved. In particular,under certain conditions the visibility can be almost as high as 100%,which is much better than the visibility limit of 1/3 in traditional GI.[34]The dependence of the SNR,visibility,and resolution on the number of iterations is also analyzed.

The experimental scheme is depicted in Fig.1. Here,for convenience and without loss of generality, in the following theoretical introduction we only consider the intensity along the horizontal direction. To begin with,if both the spatial filtersBFi(i=1,2) and the object are removed, the setup will become a traditional Hanbury Brown and Twiss (HBT) system. When the data are recorded in a discrete form in time by charge-coupled devices(CCDs),the normalized second-orderintensity correlation function for HBT can be written in the form of a summation instead of an integration as

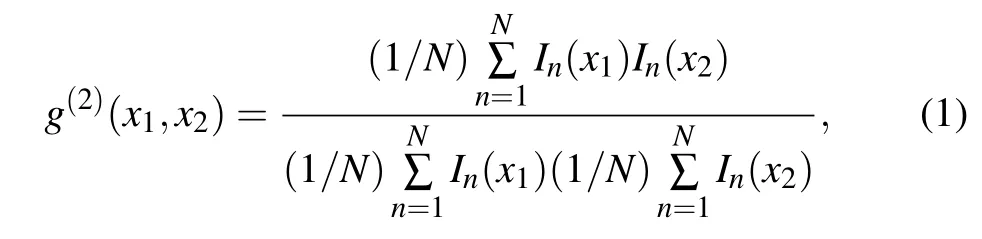
whereIn(xi) (i=1,2) are then-th intensity distributions at distancesxi(i=1,2) on theX1andX2planes, respectively,and the distancesz1andz2from the light source to the CCD planesX1andX2are equal;Nrepresents the total sampling number. If only two filters are removed and the object is still left in front of CCD1, which we take to be the bucket detector, the corresponding ghost image in a traditional GI system is given by

whereSn=∑x1In(x1)T(x1) is the total intensity of then-th measurement collected by CCD1 andT(x1) is the transmission function of the object.

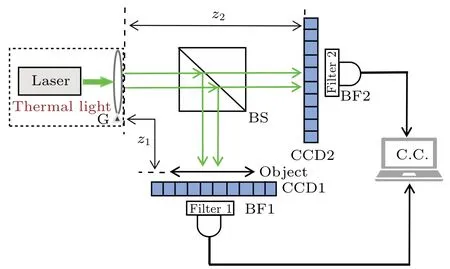
Fig. 1. Schematic diagram of experimental setup. G: ground-glass plate;BS:beam splitter;CCD1 and CCD2: spatially resolving cameras;BF1 and BF2: spatial bandpass filters.

However, if two spatial filters BF1 and BF2 are inserted behind the spatially resolving detectors CCD1 and CCD2,respectively before connection to the coincidence circuit,the instantaneous intensity distributions that are actually measured after filtering are modified as, whereFdenotes the lower and upper boundsFBLandFUL, respectively,of a bandpass filter of bandwidthB, andBis defined asB=FBU−FBL+1. Then the normalized second-order intensity correlation function after bandpass filtering becomes[26,27]

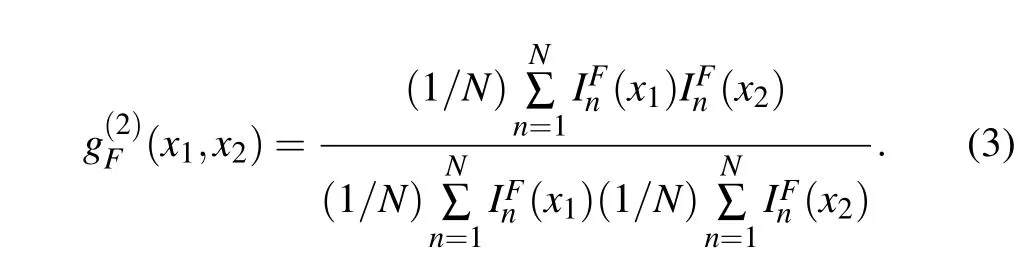
Obviously, this method is also suitable for the highpass and lowpass filters whenFjust needs to be defined as the threshold. When CCD1 together with bandpass filter BF1 play the usual role of a GI bucket detector, and the object is inserted in front, then the total transmitted intensity is, and the ghost image reconstructed withfrom the normalized second-order intensity correlation function can be expressed as

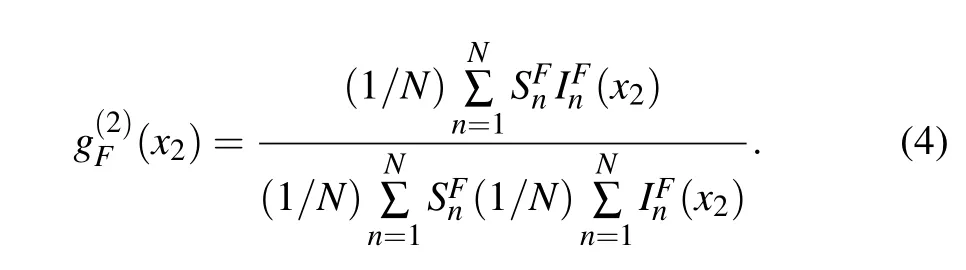
We can see that these equations have the same form as the traditional GI equations when the filtered intensities are replaced by thermal intensities.

The principle of iterative FGI is simple in that its formula has the same form as that in GI and FGI. Suppose thatMis the number of different lower boundsFk(k=1,2,...,M) ofB,so the effective sampling number actually becomesN×Mif all the filtered intensities are used to reconstruct the image of an object in the framework of GI.It seems that all the filtered intensities in the two beams and their correlations are added according to the differentFk(k=1,2,...,M), so we call the method iterative FGI. Accordingly, the normalized intensity correlation functions of the iterative filtered HBT and GI can be respectively written as

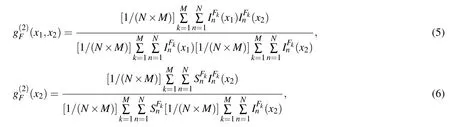
To characterize the image quality quantitatively,the visibility and SNR[35]can be defined,respectively,as

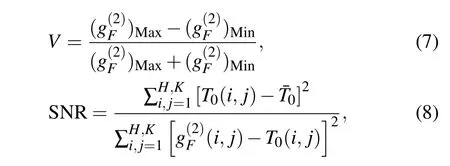
whereT0(i,j) is the transmission matrix of the object mask of sizeH×K,is the retrieved image, andT0=is the average gray-scale value of all the pixels ofT0.

3. Experiments and results

Figure 1 shows the experimental setup,which is a generic FGI system using thermal light. Pseudothermal light is generated by illuminating a rotating ground-glass plate G with a laser beam of wavelengthλ=532 nm and beam diameterD=3 mm. The pseudothermal beam is divided by a 50:50 nonpolarizing beam splitter(BS)into two spatially correlated beams;one beam is transmitted into the reference arm and the other is reflected into the test arm, to be detected by cameras CCD2 and CCD1 (Imaging Source DMK 42BU02), respectively. The data from each detector is fed into an electronic filter and then saved to a computer. However, for simplicity the data from each detector are actually saved to a computer first,and then the procedure of filtering the intensity distributions is performed by means of data processing through matrix manipulation.[26,27,33]The actual operations are as follows: first, we choose two different numbersFBLandFBUas the lower bound and upper bound, respectively. Their difference plus 1,i.e.,FBU−FBL+1, is the bandwidthB. Second,each instantaneous intensity value of thermal light is compared with a given lower and upper bound;if this value is lower than the lower bound or larger than the upper bound, it will be set to 0;if it is smaller than or equals the upper bound and larger than or equals the lower bound, it will not be changed. Finally, the filtered data are used to calculate the second-order correlation functions,as in traditional GI.

To test our method, a digital grayscale object[36]was used to simulate traditional GI, lowpass, highpass and bandpass FGI in an autocorrelation scheme according to Eq.(4).[26]The object was a simulated grayscale butterfly transmission mask of size 101×101 pixels,as shown in Fig.2(a). The reconstructed images after averaging overN=5×104exposure frames for GI,lowpass,highpass and bandpass FGI are shown in Figs.2(b)–2(e),where the SNR values are 2.67,1.95,2.58,and 1.82,respectively.The thresholds of the lowpass,highpass and bandpass filters were set toFL=5,FH=100,andFBL=20 at a bandwidthBof 1, respectively. Although it seemsthat the SNRs decrease a little bit after filtering,the recovered images are still much clearer compared with GI,especially after bandpass filtering, mainly because FGI has much better resolution. Furthermore, FGI also gives much better visibility than GI;in Figs.2(b)–2(e)the visibilities are 2.8%,10.6%,20.4%,and 5.4%,respectively. The retrieved images shown in Figs. 2(f)–2(i) were obtained from Eq. (6), and have an SNR of 1.82,2.07,4.02,and 8.14 after 15,5,11 and 21 iterations,with a visibility of 5.4%,5.5%,5.3%,and 8.0%,respectively.It is evident that the image quality gradually becomes better and better as the number of iterations increases; in particular Fig. 2(i) is almost as good as the original object. Figure 2(f)was recovered according to Eq.(6)after 15 iterations using a fixed lower and upper bound of 20 and 22, respectively, at a bandwidth of 1. It appears to be exactly the same as Fig.2(e),which can also be inferred from Eq.(6).Therefore,none of the quality parameters(SNR,visibility and resolution)can be improved by iterations for an unchanged lower bound at a fixed bandwidth. This is also true for traditional GI.However,both the SNR and visibility of the images in Figs. 2(g)–2(i), reconstructed by iterative FGI with different lower bounds at a fixed bandwidth of 1 are greatly enhanced. This fully proves the effectiveness of our iterative method in improving image quality. It should be noted that the lower bound is changed in step lengths of 5, though of course any other step length can also be used. To further verify how iterative FGI can enhance image quality,the dependence of the SNR on the lower bandpass bound and the number of iterations were measured. As illustrated in Fig. 3, the black solid line and diamonds represent the SNR of GI;the red dots,blue stars and green triangles represent the SNR of FGI with bandwidthsBof 5,10,and 15,respectively. It can be seen from Fig. 3(a) that, as the lower bound increases, the SNR of the FGI images fluctuates and decreases somewhat compared to GI in most cases. It seems that the SNR increases with the increase of bandwidth but not so significantly. However, iterative FGI can greatly improve the SNR as shown in Fig.3(b),in which as the number of iterations increases the SNR stays below that of GI and does not increase obviously at the beginning,but later increases rapidly to a maximum and then gradually deceases. Here,the increase is largely due to the increase of the effective sampling number.However,a thermal field has a negative exponential statistical probability for its intensity,so as the lower bound is raised and the bandwidth decreased the amount of signal data collected is reduced,resulting in a lower SNR.

Fig.2. (a)Digital greyscale object; reconstructed image(s)with SNR(s)of(b)2.67 by traditional GI;(c)1.95 by lowpass FGI(FL =5); (d)2.58 by highpass FGI (FH =100); (e) 1.82 by bandpass FGI (FBL =20 at a bandwidth B of 1); (f) 1.82 by iterative bandpass FGI with 15 iterations with no change of thresholds; (g), (h), and (i) 2.07, 4.02, and 8.14 by iterative bandpass FGI using 5, 11, and 21 iterations with different thresholds,respectively.

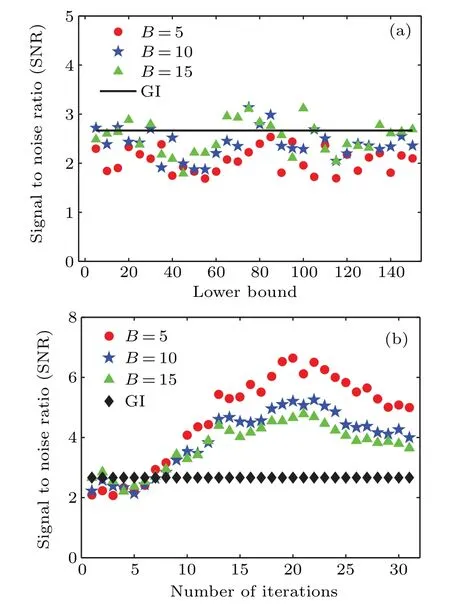
Fig.3. (a)Relationship between SNR and lower bounds of bandpass bandwidth. (b)Relationship between SNR and number of iterations.

Fig.4. Relationships between(a)visibility,(b)resolution and iterations.

The dependence of visibility and resolution on the number of iterations is shown in Figs. 4(a) and 4(b), where the red dots, blue stars and green triangles represent the visibility and resolution of the FGI for bandwidths of 1, 3, and 5,respectively. It can be seen from Fig. 4(a) that the visibility initially increases rapidly then levels off gradually as the number of iterations increases. It is significant that the visibility can greatly surpass the theoretical limit of 1/3 for thermal GI, and can almost reach 100% when the bandwidthB=1.The calculated/measured relationship between the resolution and number of iterations is shown in Fig. 4(b), which is obtained by calculating the full width at half maximum of the2nd-order autocorrelation functions of the intensity distribution from Eq. (5). The resolution initially decreases sharply and then levels off to a stable value with increase of the number of iterations. On the other hand, it can be improved by decreasing the bandwidth. It is worthy to note that the best resolution can be as fine as one pixel of a CCD device.[33]The light field after filtering does not obey the Bose–Einstein statistics of thermal light anymore,so the visibility limit of thermal light GI is no longer valid and may be exceeded. However,the reason for the improvement of visibility in FGI and iterative FGI is as yet not very clear, and awaits a more precise analytical investigation.

Though iterative FGI has advantages in many aspects as discussed above,it still has the traditional GI drawback of long integration times. It is known that compressed sensing (CS)can greatly reduce the number of exposures required in GI,so an interesting question is whether it is also effective for iterative FGI. We therefore performed a simulation experiment to image the butterfly under the same conditions as above but using a CS algorithm. The results are shown in Fig.5,where the first row shows images retrieved with a sampling number of 1000, which is about 10% of the Nyquist limit. It is evident that the details of the butterfly cannot be distinguished by CS applied to traditional GI (Fig. 5(a)), while they become quite clear in FGI with CS (Fig. 5(b)), and in iterative FGI with 5 iterations plus CS (Fig. 5(c)). The images in Figs. 5(d)–5(f) are reconstructed with CS by 30, 50, and 100 iterations for a sampling number of only 100, which is less than 1%of the Nyquist limit. We can see that the quality becomes better and better with the increasing number of iterations,which again verifies the effectiveness of iterative FGI.As mentioned above, this is because the effective sampling number is increased through iteration,though the actual sampling number is still small. Since the detection matrix that is built in the CS programming of GI can be as large as or even much larger than in the case of the Nyquist limit,we can make a trade-off between the number of exposures and iterations,choosing the optimum values for a particular need.

Fig.5. First row: images retrieved by(a)CS,(b)FGI with CS,and(c)iterative FGI with CS with 5 iterations for a sampling number of 1000.Second row: images retrieved by(d)30 iterations,(e)50 iterations,and(f)100 iterations for a sampling number of 100.

4. Conclusions

In conclusion, we have demonstrated an iterative bandpass filtered GI method that can retrieve a super-resolution image of a grayscale object, without detriment to the SNR and visibility. The scheme can be easily implemented without adding any complex equipment, and although more computational time is required this should not be a major problem since computer processing speeds are always rapidly increasing. Furthermore, by combining iterative FGI with CS,the sampling number can be reduced to less than 1% of the Nyquist limit so the computational time is also greatly reduced; together this could overcome all of the main bottlenecks in real applications of GI.We expect that iterative FGI will be applicable not only to lensless GI of any wavelength but also to all fields of optical imaging where high quality is necessary.

Acknowledgements

Project supported by the National Key Research and Development Program of China(Grant No.2018YFB0504302),the National Natural Science Foundation of China (Grant No.61975229),and Civil Space Project(Grant No.D040301).