Numerical study of growth competition between twin grains during directional solidification by using multi-phase field method

Chang-Sheng Zhu(朱昶胜) Ting Wang(汪婷) Li Feng(冯力)Peng Lei(雷鹏) and Fang-Lan Ma(马芳兰)

1School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China

2State Key Laboratory of Gansu Advanced Processing and Recycling of Non-Ferrous Metal,Lanzhou University of Technology,Lanzhou 730050,China

A multi-phase field model is established to simulate the growth competition and evolution behavior between seaweed and columnar dendrites during directional solidification. According to the effects of surface tension and interfacial energy,we quantitatively analyze the influences of factors such as inclination angles,pulling velocity,and anisotropic strength on twin growth. The results demonstrate that the pulling velocity and anisotropic strength have an important influence on the morphology and evolution of the seaweed and dendritic growth. The low pulling velocity and anisotropic strength are both key parameters for maintaining the stable morphology of seaweed during competitive growth in a bicrystal, showing that the lateral branching behavior is the root of the dendrites that can ultimately dominate the growth. And it is clarified that the lateral branching behavior and lateral blocking are the root causes of the final dominant growth of dendrites. With the increase of anisotropy strength, the seaweed is eliminated fastest in case 1, the seaweed is transformed into degenerate dendritic morphology,and eliminates the seaweed by promoting the generation and lateral growth of the lateral branches of the dendrites. The increase of pulling velocity is to increase the undercooling of favorable oriented grain and accelerate the growth rate of dendrites,thus producing more new primary dendrites for lateral expansion and accelerating the elimination rate of unfavorable oriented grain.

Keywords: multi-phase field simulation,grain growth competition,directional solidification,twin grains

1. Introduction

In the process of directional solidification, thermodynamic simulation of its microstructure is a popular direction in developing the material science and computer science.[1]The solidification structure formed during the solidification process is a key factor in determining the material properties. Owing to the close relation between the performance of the material and its microstructure, the development of science and technology relies heavily on the development of new material systems,through improving or designing microstructures to meet the requirements for advancing technology.[2]The growth competition among grains of different orientations is a common phenomenon in the evolution of microstructures.Therefore,understanding the mechanism of grain growth competition with different orientations, clarifying the factors that affect growth competition,and then controlling the process of grain competition growth, will play a vital role in determining the performance of castings and material preparation.[3]According to the analysis of the difference in the extent of undercooling of the columnar dendrite tip in the tip solidification process, Walton and Chalmers[4]proposed a classic competitive growth model, and Rappaz and Gandin[5]briefly summarized the model. The results show that the lower extent of undercooling ensures the superiority of the favorable oriented grains in the competition, so that the unfavorable oriented grains with higher cutting-edge undercooling should be eliminated. However, the above analysis of competitive growth is just based on the dendrite region, and the research on the growth competition between different morphological grains is less understood. Therefore, the present work focuses on the competitive growth of seaweed and dendritic.The grain growth direction of the directional solidification process is determined by two characteristic directions,namely the thermal gradient direction and favorable oriented growth direction.The angle between these two directions is usually defined as the misorientation angleΘ0.

A large number of experiments and theoretical studies have shown that under low anisotropy strength it is possible to grow a seaweed-like organization with the interface morphology by controlling the direction of the thermal gradient and the preferential growth direction of the grains.[6]When this misalignment angle is close to a maximum deviation value of 45°,a transition into another complex form,called degenerate seaweed, will occur.[7]However, in recent experimental studies,many experimental and simulation results were inconsistent with or even contrary to the description of the model, which makes us start to think whether the classical Walton Charmers competitive growth model is suitable for the growth competi-tion between dendrites and degenerate seaweed.[8]According to the classical model of competitive growth, the degradation of seaweed grains cannot be good for competitive growth,and with the increase of the dislocation angle, due to the higher tip super-cooling of the degenerate seaweed grains, the elimination rate decreases. Zhanget al.[9]revealed that the increase in undercooling will cause the morphology of seaweed to change drastically. However, some subsequent experimental observations have proved that the growth competition behavior between actual columnar dendrites and seaweed grains may be much more complicated. These anomalies indicated that the difference in undercooling at dendrite tips is not always suitable for predicting the growth competition between grains. The experimental results obtained by Yuminet al.[10]are consistent with our predictions. The growth velocity and the lateral branching of convergent grain boundary will have an important influence on the growth competition of seaweed and dendrites, showing that the formation of degenerate seaweed in directional solidification is affected by lower pulling velocity and higher thermal gradient.

Owing to the complexity and opacity of the microstructure of metal materials, it is difficult and time-consuming to obtain useful statistical data from hundreds of experiments,and the results obtained through experiments have great limitations. Therefore, combining numerical simulation methods to analyze the growth competition process of grains has become an effective method of studying the growth mechanism. Among them, the phase field method has become an important tool to study the mechanism and kinetics of dendrite growth due to its advantages of accurately simulating the changes of solute field and temperature field during solidification. Tourretet al.[11]established an analytical model of divergent grain boundary selection based on phase field simulation of two-dimensional (2D) and three-dimensional (3D)small sample thickness systems. Fenget al.[12]investigated the influence of the grain orientation of the parent phase on the grain growth during the solid–solid phase transition by establishing a temperature-controlled sequence function and a new multi-phase-field model. Guoet al.[13]analyzed the randomness of boundary trajectory by simulating the phase field of transparent alloy SCN-2 wt% Ace, and gave a more accurate choice of boundary direction. Xinget al.[14]studied the influence of temperature gradient and orientation angle on the evolution of grain boundary by establishing a multiphase field model, and found that the elimination rate of degenerate seaweed will increase with the increase of misorientation angleΘ0at the convergence boundary.

These studies have proved that the dendrites have better growth kinetics than the degenerate seaweed.[15]However,in the process of directional solidification, there are some problems that have not been discussed in detail, such as the dynamic behavior of dendrite branching,quantitative description of the choice of grain boundary orientation,and the competitive growth mechanism between twin grains.So far,there have been published a few reports about the competitive growth of twin grains with different values of interface energy and orientation angles,but the growth behavior between them has not been addressed in detail. Therefore,it is necessary to conduct in-depth research, hoping a more comprehensive understanding of which parameters and properties can affect the growth competition mechanism and the elimination rate. In this work,we explore a 2D multi-phase field simulation method by setting up a bicrystal model with different orientation angles to conduct an in-depth study of the growth competition between columnar dendrites and degenerate seaweed. Different growth patterns are obtained by changing the pulling velocity and anisotropic strength of the dendrite tip. The elimination rate of degenerate seaweed and the evolution of convergent grain boundary are analyzed in detail.

2. Establishment of multi-phase field model

2.1. Phase field equation and solute field equation

In order to distinguish grains with different morphologies and orientations, in this study we use the binary metal alloy multiphase field model developed by Ofori–Opokuet al.,[16]coupled temperature field and solute field, to investigate the growth competition and the evolution of grain boundary. In this model, multiple order parameters from−1 to 1 can be introduced to characterize the multiple grains of different shapes and orientations(1≤i ≤N),whereNis the total number of the grains, thus forming a phase field parameterφ=(φ1,φ2,...,φN),eachφi=1 presents the solid phase andφi=−1 presents the liquid or the solid in the bulk of the other grains. The multi-phase field equation and solute field equation in the directional solidification process are given as follows:

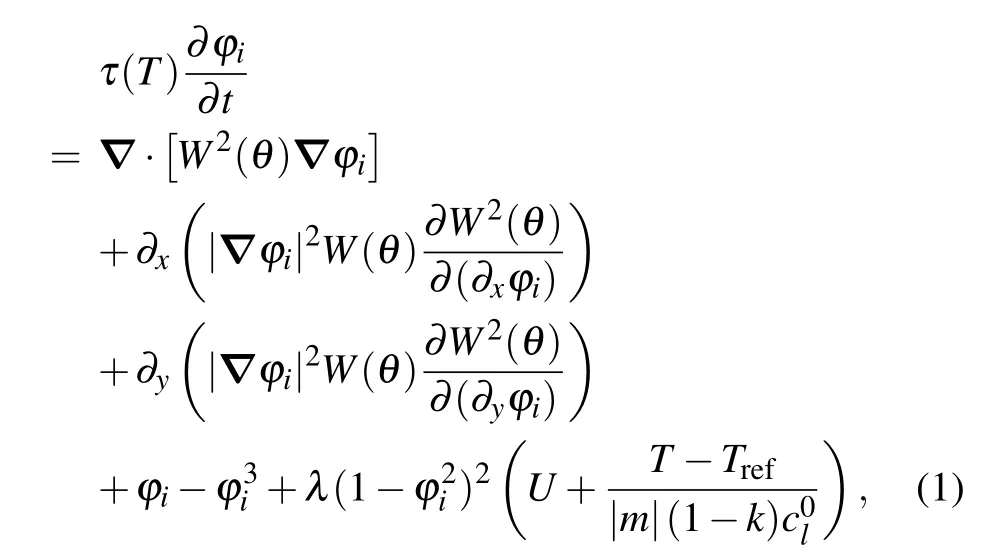
whereθis the angle between the direction normal to the interface of thei-th grain and the thermal gradient direction,the concentration on the liquid side of the solid–liquid interface,λis the width of the diffusion interface, andΘi0is the misorientation angle of thei-th grain, then theanisotropic equation about the interface energy is as follows:

The solute field equation, where the solid diffusion is neglected but the anti solute collapse flow term is added to eliminate the non real interface effect,is as follows:

whereDlis the liquid diffusion coefficient andkis the solute partition coefficient. The supersaturated fieldUobtained by solving the solute conservation equation is

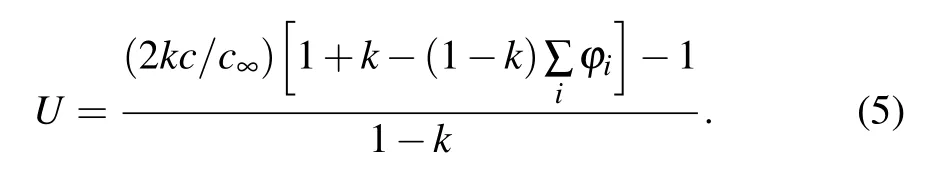
The anti-trapping current term in Eq.(4)is

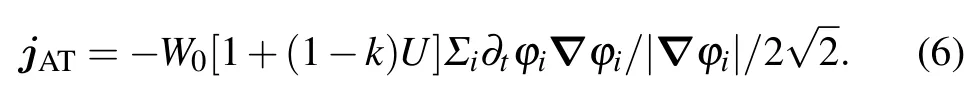
For the SCN crystal with cubic symmetry, the solid–liquid interface energy anisotropy in a 2D system can be described as

whereε4is the strength of anisotropy,as=1−3ε4.

In Eq. (5),Uis a supersaturation field with respect to（,T=Tref+G(x−Vpt)replaces the temperature field.Here,Trefis a reference temperature,xis the position in the axis of solidification,andq(φ)=(1−Σiφi)/2 modulates solute diffusion across the interface. In the multiphase field model,time scaleτ0and length sizeW0can be determined by the two relations:andd0=a1W0/λ,respectively, whereis the capillary length,a1=0.8839 anda2=0.6267 are two constants determined by selecting the free energy function in the phase field model.[17]In the following simulations, in order to introduce thermal fluctuations to destabilize the solid–liquid interface,we added a random noise ofto the values of all order parameter fields at each point(i,j)and in each time step, and hence the value of order parameter field in the next time step can become

whereγI,Jis a random number in a range from−0.5 to 0.5,Mis the noise magnitude,Δtis the time step. Different magnitudes of the noise lead to different ways of grain boundary evolution due to the noise induced side branching behaviors.Therefore,we fix the noise magnitudeM=0.01 for all grains.

2.2. Physical parameters

In this paper, we explore the SCN-0.24-wt% camphor model alloy[18]as the research object. Considering the complexity of calculating the multiphase field governing equations, the phase field equation (1) and the solute field equation(3)are nondimensionlized by using dimensionless factorsτ0andW0in time and space, respectively. Determine a dimensionless parameterξ=45.25, the width of the interface layerξ=W0/d0,andλ=a1ξ,the value of which is 40,then we will obtain the following formulas:. The pulling velocity of the isotherm isVp=R/G,and the dimensionless expression is. In this model,we assume that the solute diffusion in the solid phase is negligible. The calculation parameters required for the simulation of the directional solidification process are shown in Table 1.

Table 1. Parameters of bicrystal directional solidification simulation.

2.3. Numerical calculation method

We explore the explicit finite difference method on a uniform grid to discretize the multiphase field model,and the time discretization uses an explicit first-order forward Euler equation to solve Eqs.(1)and(3),and the Laplace operator uses a nine-point scheme to reduce the effect of grid anisotropy. The time step is set to be Δt=0.002τ0. Under the condition of ensuring the convergence of the calculation results, the computational domain should be large enough to ensure the full growth of dendrites. Therefore, the calculation area is set to be 800 µm×600 µm, and the primary spacing between the two grains is taken as 400µm,the grid spacing is Δx=0.8W0,and no-flux (or reflection) boundary conditions are imposed on the domain boundary,and the diffusion interface thicknessξ=W0/d0is taken to be sufficiently small to obtain the accurate results.

2.4. Orientation characterization of two grains

Two seeds are assembled as shown in Table 2.Two grains with radiusR=40µm are arranged on thex+axis of the simulation calculation area,and the positions of grain A and grain B are located atx=600 µm and 200 µm respectively. AnglesθAandθBare defined to be counterclockwise with respect to the growth directiony+. Table 2 shows the cases of threedifferent angle settings. Previous experimental and numerical studies have shown that the larger the stagger angle,the lower the pulling velocity is,and the more seaweed structure is likely to be formed during directional solidification. So for grain A,we fix the orientation angleθA=−45°andθA<θB.

Table 2. Orientation characterizations of two grains.

3. Numerical results and discussion

According to previous studies on the competitive growth process between dendrites,it is generally believed that the favorable oriented grain can squeeze the growth space of unfavorable oriented grain through the continuous generation of new dendrite arms and eventually make it eliminated. However,the current research is limited to the competitive growth of dendrites, and most of them are understood qualitatively only. There are too few quantitative studies on the competitive growth of multiphase grains with different pulling velocities and anisotropic strengths. Therefore, in this section the multiphase field model is used to study the influences of angles,anisotropic strengths and pulling velocities on the competitive growth process of seaweed and dendrites.

3.1. Effect of orientation angle on competitive growth of seaweed and columnar dendrites

3.1.1. Convergent growth under diあerent orientation structures

It can be seen from Figs. 1(a1)–1(a4) that the grain boundary existing between the seaweed and dendrites is not smooth. And grain A (red one) is gradually degenerated by the growth of the grain B (blue one). When the grain A is close to the left side of dendrite B1 of the grain B, the grain A is blocked,and the dendrite B1 continues to grow and form secondary arm dendrites occupying the growth space at the front tip of the seaweed,forming a lateral impact to gradually dominate the competitive growth process,until it occupies the entire growth area. The microscopic enlargement of the grain boundary is presented in Fig.1(a4). It is found that when the newly grown secondary dendrite develops to the grain boundary,the grain boundary inclines from grain B to grain A.

The simulation results of Figs. 1(b1)–1(b4) show that the grain B also dominates the competitive growth process,and the grain boundary inclines to grain A. As shown in Fig.1(b1),the initial seaweed is more affected by the dendrite withθB=15°than withθB=0°, which is directly blocked by the inclined dendrite at the grain boundary. When developing to Fig.1(b3),the grain B overgrows grain A and occupies the whole growth area. As shown in Fig. 1(b4), the microscopic magnification of the grain boundaries shows that the converging grain boundary systematically follows the orientation of the neighboring dendrite. In this case,the new primary arm dendrites are produced and rapidly expand laterally, occupying the growth space of grain A and prompting the rapid elimination of degenerate seaweed.

Fig.1. Microstructures of dendrites and seaweed during competitive growth of SCN-0.24-wt%camphor model alloy with ε4=0.01 in the plane at time t =1000τ0, 2000τ0, 3000τ0: (a1)–(a4) θB =0°, (b1)–(b4) θB =15°, and(c1)–(c4)θB=−15°.

For case 3 in Table 2, the microstructure evolutions are displayed in Figs.1(c1)–1(c4). In Figs.1(c1)–1(c3),the grain B gradually overgrows the grain A,but it shows different characteristics. In the initial stage, the grain A is less affected by the grain B. However, through the magnification of the microstructure at the grain boundary in Fig.1(c4), it can be observed that in the enlarged view of the microstructure at the grain boundary,some secondary arm dendrites are formed on the left side of the B1 dendrite of grain B. The new dendrite and secondary arm dendrite developed from grain B at the grain boundary cause the grain boundary to gradually incline from grain B to grain A,and finally eliminate the seaweed.

3.1.2. Influence on grain boundary angle

Figure 2 shows the evolutions of grain boundary(GB)angles at the interface anisotropic strengths of 0.01, 0.03, and 0.05 for various misorientation angles at the same time,whereθGBis determined by tan(θGB)=R/H,withRreferring to the seed width(40µm)andHrepresenting the distance from the initial position to the terminating position. AngleθGBis positive, meaning that degenerate seaweed will always be eliminated by dendrites over time,which is consistent with the prediction of classical competition model. In addition, andθGBis not only affected by the dendrite orientation, but also by the anisotropic strength. As shown in Figs.2(a)and 2(c), forcase 1 and case 3, with the increase of anisotropy strength,theθGBand the elimination rate of seaweed increase. Now we come to focus our attention on the competitive growth of grain A and grain B.Combining the simulation diagram from Fig. 1, it can be seen that the phase transformation of seaweed and the lateral branching of the neighboring dendrite B at the grain boundary lead the grain boundary to incline laterally from grain B to grain A, and theθGBincreases slightly with the increase ofε4. For case 2,as shown in Fig.2(b),θB=15°,which has the orientation of inclined dendrites B.Combining the simulations of Figs.1(b1)–1(b4),when the growth of grain A is degenerated by the lateral competition of the neighboring dendrite B,θGBbasically follows the orientation of grain B,so that the grain boundary angle turn large and stable. At low anisotropy, the effect of eliminating degenerate seaweed under the convergence condition of case 2 is proved to be best and that the greater the inclination angle,the greater the elimination rate of grain A,which is basically consistent with the experimental result of Yuminet al. And then,we will specifically explore how the value ofε4changes theθGBby affecting the morphology of grain A and grain B. Meanwhile, in addition to investigating the influence of the orientation angle of grain B on the elimination rate of grain A,it is also necessary to consider whether changes of theε4and the pulling velocity exert greater influence on the elimination of grain A.

Fig. 2. Evolutions of grain boundary angles at different interface anisotropies strengths: 0.01, 0.03, and 0.05 for various misorientation angles in case 1(a),case 2(b),case 3(c).

3.2. Effect of anisotropie surface tension on competitive growth of seaweed and columnar dendrites

Extensive theoretical studies and phase field method simulations demonstrate that the anisotropy strength will significantly change the growth velocity of grains and the morphology of the interface. In this subsection, the multiphase field method is used to investigate the influence of anisotropy strength on the morphological evolution of seaweed and columnar dendritics, and reveal the physical mechanism of the morphological evolution of the twin grains interface under the influence of anisotropic strength. By setting different valuesε4=0.01,ε4=0.03,ε4=0.05,andε4=0.07 to change the twin growth morphology, its growth pattern is observed. The anisotropic strength of the interface energy is a main physical factor that controls the directional dendrites to turn into the seaweed. It can be seen from Fig.3 that the twin grains show similar growth trends under the three convergence cases,dendrites and seaweed coexist for a long period of time.At a low anisotropy strength, the tip growth of the seaweed(grain A) is weakened, and there is no obvious preferred orientation. Whenε4is increased to 0.03,i.e.,ε4=0.03,the seaweed morphology becomes more hierarchical,and there is an obvious preferred orientation. With the further increase of the anisotropy strength, the morphology of the seaweed changes greatly, the tip splitting becomes weaker, changing from irregular splitting to symmetric regular splitting, and growth is also inhibited. As shown in Fig.3(a3),atε4=0.05 the directional solidification structure changes from seaweed to degenerate dendrites (the degenerate dendrite refers to a solidified structure that has a dendritic morphology with two growth directions distributed on both sides of the thermal gradient directions). At this time,the actual growth direction of grain A is between the preferred orientation and the thermal gradient direction.Atε4=0.07,the morphology of the solidified structure becomes inclined dendrite, its primary arm dendritic has a unique growth direction, and the angle between it and the thermal gradient direction is measured to be 35°. In the angle between the two sides,the primary arm of the dendrite in a direction of 35°has more obvious advantages than in a direction of−37°. The latter will gradually be eliminated,thus forming inclined dendrites with a unique growth direction. Therefore,low anisotropic strength is an important condition for maintaining the morphology of seaweed.

According to Figs.3(a1)–3(a4)and 3(c1)–3(c4),with the increase of anisotropy intensity,the lateral branching becomes more developed. At the junction of the twin grains,columnar dendrites squeeze the space where the seaweed tips grow and split by generating secondary dendrite arms,which causes the grain boundary angle in Fig. 2 to increase with the increase ofε4. Whenε4increases to 0.07, a large number of tertiary dendrite arms are generated from secondary dendrites, some of which are eliminated, and some will develop into stable primary arm dendrites along the growth direction. Although dendrites prevent the seaweed from growing, compared with the other two cases, in case 1 (Fig. 3(a)), grain B produces more primary dendrites, and the growth direction of new tertiary dendrites is consistent with the thermal gradient direction,and the growth velocity of dendrites is significantly faster than those in the other two cases, which increases the rate of elimination of seaweed.In case 2,some new inclined primary dendrite grow at the grain boundary,leading the grain boundary to turn to grain A,which has a weaker effect on the growthof seaweed than in the other two cases. It can be seen that the interaction between the twin grains is affected by the inclination angle of the dendrite. The smaller the inclination angle of the dendrite and the closer to the thermal gradient direction the growing direction of dentrite,the smaller the distance between adjacent tips and the smaller the distance between the dendrites,the stronger the effect will be.In summary,the comparisons among the evolutions of twin grains competition growth in the three cases indicate that the best effect on the elimination of seaweed is embodied in case 1 with the increase ofε4.Moreover, the comparison of the growth evolution between the twin grains shows that the increase in anisotropy strength is beneficial to the growth of lateral branches and makes the seaweed crystals undergo the phase change, thereby enhancing the inhibitory effect on the growth of the seaweed, and accelerating the elimination of grain A.Therefore,we will investigate the factors that affect the deformation of seaweed and explore the conditions for maintaining stable seaweed later.

Fig.3. Competitive growths of grain A and grain B at various strengths of interface anisotropy ε4 for case 1(a),case 2(b),case 3(c).

Fig. 4. Positions of grain boundary in x direction for various strengths of interface anisotropy.

Since the best competitive growth effect is embodied in case 1, the influences of different anisotropy strengths on the values of twin grains under case 1 will be discussed. It can be seen from Fig. 4, with the increase ofε4, the position of the grain boundary in thexdirection shows the trend of“increasing-decreasing-increasing”. After the initial stage of growth from Fig. 5, the dimensionless tip undercooling of grain A and grain B both oscillate with time. However, the dimensionless tip undercooling of grain A always maintains a larger value than that of grain B.Since the undercooling would affect the growth velocity of grains,the seaweed grows better than the columnar dendrites and expands rapidly around the growth area,showing a competitive advantage over a period of time. Therefore, the grain boundary has a“decreasing”trend in thexdirection. Finally, the columnar dendrites begin to show the advantages of growing with time,namely the lateral growth is achieved by generating a new secondary and tertiary arm,and the grain boundary reflects the trend of“increasing”.

The microstructure in Fig. 3(a1) and the “black line” in Fig. 4 both show that the position of the grain boundary in thexdirection atε4= 0.01 is in regular oscillation. Since the columnar dendrites have no side branches,twin grains can better maintain co-growth at the growth interface. Asε4increases,the grain boundary continuously moves to the position of the grain A, which speeds up the elimination rate of grain A.As shown in Fig.6,the increase ofε4will increase the undercooling of grain B,and its growth rate will increase,but the tip radius will decrease,and the dendrites will gradually begin to be refined. The tip radius is a minimum value atε4=0.04,which leads more secondary arms to laterally grow, and thus squeezes the growth space in front of the grain A, indicating that the growth advantage of columnar dendrite is embodied here most obviously.

Fig.5. Curves of time-dependent dimensionless tip undercooling of grain A and grain B for various strengths of interface anisotropy.

Fig. 6. Curves of dimensionless tip radius and undercooling versus ε4 for various strengths of interface anisotropy.

At the same time, the value of the tip radius of the seaweed decreases sharply and then tends to be stable. With the morphology of seaweed atε4=0.05 (Fig. 3), we can know that the seaweed begins to undergo the phase transformation,and is transformed into degenerate seaweed. This reflects that the columnar dendrites grow better than seaweed in the competitive growth process,and seaweed is eventually eliminated.In short,ε4is an key factor that affects seaweed to maintain its own shape. Asε4increases,grain A will gradually degenerate into the degenerate mode,the tip radius will decrease rapidly,and the split will become weaker. In summary,asε4increases,the elimination of seaweed is accelerated mainly through its own phase change and promotion of the lateral branch growth of dendrites.

In order to obtain the seaweed under the optimal growth environment, the anisotropic strength is chosen to be 0.01 in the following simulation calculations on the effect of the pulling velocity(Vp)on the interface morphology.

3.3. Effect of pulling velocity on competitive growth of seaweed and columnar dendrites

We use the multiphase field method to simulate the directional solidifications at pulling velocities of 5, 10, 15, and 20 µm·s−1, and analyze the solid–liquid interface morphology and the evolution of the structure in the directional growth zone. Figure 7 shows that the twin grains in the front of the alloy solidification interface present different immature growth morphologies forVp=5µm·s−1. The grain A on the left is in a seaweed shape and the grain B on the right appear as cellular crystals with small spacing in between. The solid–liquid interface grows forward and the twin grains show stable growth instead of competing evolution at the crystal interface. ForVp=10µm·s−1, a relatively stable competitive growth interval is formed, and the front edge of the alloy solidification interface gradually begins to transform. The grain A grows into a seaweed shape,while the grain B grows into a dendritic shape. As the pulling velocity further increases, the seaweed degenerates into columnar crystals, and then become irregular cellular crystals, whose direction changes into the direction of the thermal gradient, and eventually is eliminated by the dendrites. For the grain B on the right side of the growth interface,the increase in the pulling velocity causes the solid–liquid interface to undergo a “cellular crystals–dendritic–fine dendritic” evolution process. The distance between the primary dentrite and secondary dendrite continues to decrease.With the increase of the pulling velocity in the three cases,the position of grain boundary in thexdirection moves to that of grain A,and grain B produces many gradually refined primary dendrites,which speeds up the elimination of seaweed.

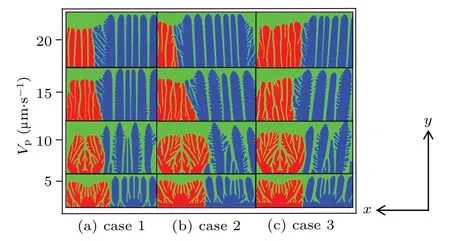
Fig. 7. Competitively growing grain A and grain B at various values of pulling velocity(Vp)for three cases: case 1(a),case 2(b),and case 3(c).

From the simulation results, we can conclude that the seaweed can maintain a better growth morphology atVp=10 µm·s−1andε4=0.01, that is, lower pulling velocity and anisotropic strength are both important factors for maintaining the morphology of the seaweed shape in the growth of twin grains. IncreasingVpwill cause the seaweed to deform and accelerate the rate of elimination.

From Fig. 8 it follows that as the pulling velocity increases, the dimensionless tip undercooling of dendrite B rapidly increases, the growth rate of columnar dendrites increases, the primary dendrite spacing becomes smaller, the tip radius of the dendrite decreases, and the columnar dendrites continue to be refined. The growth of the secondary and tertiary arms will also accelerate the lateral expansion of the dendrite B. It is worth noting that a most important factor inaccelerating the elimination rate of grain A is the increase in the number of new primary arm dendrites. Especially when the pulling velocity continues to increase by 30 µm·s−1and above, the grains A and B show the morphology of stable columnar dendrites,the columnar dendrites become finer and their number increases. Finally,the grain B slowly eliminates the grain A.

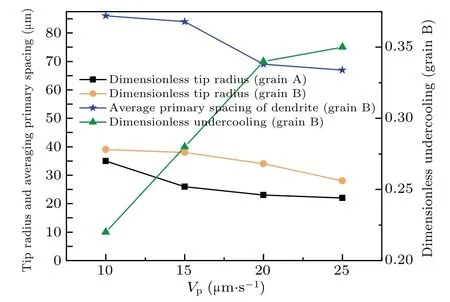
Fig. 8. Variations of dimensionless tip radius of grain A and grain B, undercooling(grain B)and averaging primary spacing(grain B)with pulling velocity.

It can be seen from the above analysis that the Walton–Charmers’competitive growth model is basically applicable to the growth competition between dendrites and seaweed. Degenerate seaweed cannot survive in the competitive growth,but it cannot be explained only by the difference in undercooling among the tips of dendrites. The real competitive growth is more complex, involving with the phase transition of seaweed,the lateral branching behavior,and the lateral blocking of dendrites. This study confirms that the competitive growth of twin grains is affected by factors such as orientation angle,pulling velocity and anisotropic strength. In the future, more factors, such as Peclet number, interdendritic flow,etc. need to be added for further study. The 3D competitive growth between dendrites and seaweed at the diverging and converging grain boundaries are also worthy of further investigations.

4. Conclusions

(i) A comparison among the evolutions of twin grains’competition growth under three cases shows that asε4increases, the best effect on the elimination of seaweed is embodied in case 1,in which more dendrites and the fastest growing tertiary arm dendrites along the thermal gradient are created,therefore hindering the seaweed from growing.

(ii) Lower pulling velocity and anisotropic strength are both important factors to maintain the morphology of seaweed in the growth of twin grains competition growth. They have different effects on the seaweed. Asε4increases,the seaweed gradually transforms into degenerate dendrites, while the increase of the pulling velocity causes the seaweed to transform into columnar dendrites that grow along the thermal gradient.

(iii)Asε4increases,the dendrites accelerate the elimination rate of seaweed by promoting the growth of their lateral branches;higher pulling velocity will increase the undercooling of dendrites and accelerate the growth rate of dendrites,to produce more new primary arm dendrites, thus making grain A faster to be eliminated.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 52161002, 51661020, and 11364024), the Postdoctoral Science Foundation of China(Grant No. 2014M560371), and the Funds for Distinguished Young Scientists of Lanzhou University of Technology,China(Grant No.J201304).