A new direct band gap silicon allotrope o-Si32

Xin-Chao Yang(杨鑫超) Qun Wei(魏群) Mei-Guang Zhang(张美光)Ming-Wei Hu(胡明玮) Lin-Qian Li(李林茜) and Xuan-Min Zhu(朱轩民)

1School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China2College of Physics and Optoelectronic Technology,Baoji University of Arts and Sciences,Baoji 721016,China3School of Information,Guizhou University of Finance and Economics,Guiyang 550025,China

Silicon is a preferred material in solar cells, and most of silicon allotropes have an indirect band gap. Therefore, it is important to find new direct band gap silicon. In the present work, a new direct band gap silicon allotrope of o-Si32 is discovered. The elastic constants, elastic anisotropy, phonon spectra, and electronic structure of o-Si32 are obtained using first-principles calculations. The results show that o-Si32 is mechanically and dynamically stable and is a direct semiconductor material with a band gap of 1.261 eV.

Keywords: first-principles calculation,elastic anisotropy,silicon

1. Introduction

Among all renewable resources, solar energy is safe,adaptable to the region and climate, inexhaustible, and also is one of the cleanest and most sustainable forms of energy that people are seeking in the 21st century. As a new energy source, solar energy can be converted into electricity, so it is essential to develop the efficient photovoltaic materials. Owing to its abundant storage and good structural stability,silicon is widely used as a photovoltaic material. Elements belonging to the same main group usually have similar chemical properties,but there are also some significant differences between them. Pure silicon and pure carbon exist in nature in the same form of diamond, and they both exhibit the ideal tetrahedral coordination. Carbon, silicon, and germanium are known to have many allotropes. For diamond silicon, the indirect narrow band gap (1.12 eV) limits the conversion efficiency of solar energy, whereas the direct wide band gap (3.4 eV) limits the absorption of low energy photons.[1]Therefore, some metastable silicon allotropes with indirect band gaps, such asC2/m-16,R8,P2221, andT12-Si structures, have been reported.[2—6]Owing to the limited performance of these materials in absorbing solar energy, the search for new siliconbased semiconductor materials with direct band gap has become a hot topic.

Recently, several silicon allotropes with direct band gap have been proposed.[7—12]Bottiet al.[12]have presented a number of quasi-direct band gap silicon allotropes with lower energy of formation, which exhibit better optical properties than cubic silicon. Thus, these allotropes are more efficient in absorbing solar energy. Usingab initiocalculations,Wanget al.[11]predicted six silicon metastable allotropes that can be applied to multiple p—n junction photovoltaic modules.These crystals are direct band gap semiconductor materials and quasi-direct band gap semiconductor materials with band gaps ranging from 0.39 eV to 1.25 eV.Fanet al.[13]proposed two new silicon allotropes, namelyCm-32-Si andP21/m-Si,which are direct band gap semiconductor materials with band gaps of 1.85 eV and 0.83 eV, respectively. It was also found that their absorption spectrum and solar spectrum have a significant overlap, so they are better than diamond silicon in terms of optical performance. Guoet al.[14]discovered a type ofh-Si6 with good thermal stability,dynamic stability and mechanical stability. They also found thath-Si6 is a semiconductor material with a direct band gap of 0.61 eV,further revealing excellent optical properties. Weiet al.[15]found six new silicon phases via high-throughput calculations. They revealed that the six silicon allotropes are direct band gap semiconductor materials with band gap values ranging from 0.66 eV to 1.47 eV. TheCm-32 carbon and theP21/mcarbon both have direct band gaps. By replacing carbon atoms with silicon atoms, the obtainedCm-32 andP21/msilicon allotropes are also direct band gap semiconductors.[13]The direct band gap germanium allotrope of Ge24 is also obtained based on quasi-direct band gap Si24.[9]These two cases motivated us to look for new direct band gap silicon allotropes from carbon allotropes with direct band gap. In Ref. [16], a direct band gap G164-carbon with a band gap of 3.13 eV was uncovered.Thus,in the present work,replacing the carbon atoms by silicon atoms,a new silicon allotrope,namelyo-Si32,is obtained.We systematically study the structural stability,electronic and elastic anisotropy ofo-Si32 via first-principles calculations.In addition,we find thato-Si32 is a direct semiconductor materialwith a band gap of 1.261 eV.

2. Computational method

The plane wave pseudopotential total energy calculations of theo-Si32 allotrope were performed by using the Viennaab initiosimulation package (VASP)[17]based on density functional theory(DFT)[18,19]with the projector augmented wave(PAW)[20]potentials. In this computational scheme,the pseudopotentials were employed for the 3s23p2atomic configurations of Si. The wave function was expanded by using a plane wave basis set with 450-eV energy cutoff. In the whole Brillouin zone, the Monkhorst—Pack[21]3×7×7 grid sampling was used in calculations. The exchange-related potential was processed at the Perdew—Burke—Ernzerhof(PBE)level of the generalized gradient approximation(GGA).[22]For structural optimization,a convergence criterion require that the total energy of two adjacent steps should not exceed 10−5eV and the atomic force should not exceed 0.05 eV/.The Heyd—Scuseria—Ernzerhof(HSE06)[23,24]hybrid functional and PBE method were used to calculate the electronic structure of theo-Si32 allotrope.The phonon spectra were calculated by using the PHONOPY code.[25]

3. Results and discussion

Using the method described above, we obtain a new sp3-hybridized silicon structure with orthorhombic symmetry, namelyo-Si32 as shown in Fig. 1. This structure includes 32 atoms in a unit cell with theImma(No. 74) space group. The two inequivalent atoms occupy the Wyckoff positions of Si1 16j (0.57717, 0.57046, 0.34404) and Si2 16j(0.18589, 0.57209, 0.65406). The lattice constants ofo-Si32 area=15.517,b=6.684, andc=6.987at ambient pressure. The density ofo-Si32 is 2.06 g/cm3.

From Fig. 1 it can be seen thato-Si32 is composed of nine types of rings, namely three Si4 rings, three Si6 rings, and three Si8 rings, which are identified with different colors. From Fig. 1(a), it can be observed that there are three Si4 rings and two Si6 rings which are colored in yellow, green, purple, pink, and orange, respectively. The 2×2×2 supercell structure ofo-Si32 shows one Si6 ring and one Si8 ring, which are represented in light green and light blue, respectively, as shown in Fig. 1(b). As can be seen from Figs. 1(c) and 1(d), there are two types of Si8 rings, which are represented in light yellow and dark red,respectively. To further understand the structure, all the Si rings ino-Si32 are shown in Fig. 2. The first type of Si4 ring is shown in Fig. 2(a); it is composed of four Si1 atoms and has two types of bonds, with bond lengths of 2.3741(d1(Si1−Si1))and 2.3949(d2(Si1−Si1)),respectively. The second type of Si4 ring is composed of four Si1 atoms and has two types of bonds. In this case, the bond lengths are 2.3999(d3(Si1−Si1)) and 2.3949(d2(Si1−Si1)) as shown in Fig.2(b). From Fig.2(c),it can be seen that in the third type of Si4 ring, there are four Si2 atoms that form two types of bonds with lengths of 2.3781(d1(Si2−Si2)) and 2.3991(d2(Si2−Si2)). The first type of Si6 ring is composed of two Si2 atoms and four Si1 atoms, as shown in Fig. 2(d). These atoms form four types of bonds with bond lengths of 2.3781(d1(Si2−Si2)), 2.3485(dSi1−Si2), 2.3741(d1(Si1−Si1)), and 2.3999(d3(Si1−Si1)). As shown in Fig.2(e),the second type of Si6 ring contains four Si2 atoms and two Si1 atoms, involving four different bond lengths (d3(Si1−Si1)=2.3999,dSi1−Si2=2.3485,d3(Si2−Si2)=2.3583,andd1(Si2−Si2)=2.3781). Figure 2(f) shows four types of bonds with different lengths in the third type of Si6 ring, namely 2.3741(d1(Si1−Si1)), 2.3485(dSi1−Si2), 2.3991(d2(Si2−Si2)), and 2.3585(d3(Si2−Si2)). From Fig. 2(g), it can be seen that there are six bond lengths in the first type of Si8 ring, which ared2(Si2−Si2)(2.3991),d3(Si2−Si2)(2.3585),d1(Si2−Si2)(2.3781),dSi1−Si2(2.3485),d1(Si1−Si1)(2.3741), andd3(Si1−Si1)(2.3999). The second type of Si8 ring is composed of four Si1 atoms and four Si2 atoms,which have three bond lengths(d3(Si1−Si1)=2.3999,dSi1−Si2=2.3485,andd2(Si2−Si2)=2.3991),as shown in Fig.2(h). Like Fig.2(h),the Si8 ring in Fig.2(i)also contains four Si atoms and four Si2 atoms, and the bond constituted by these atoms have lengths ofd1(Si2−Si2)(2.3781),dSi1−Si2(2.3485), andd2(Si1−Si1)(2.3949).

Fig.1. (a)Global view of crystal structure of o-Si32,(b)2×2×2 supercell along[010]direction,(c)1×2×1 supercell along[001]direction,and(d)schematic depiction of structure, with red sphere and black sphere representing Si1 atom and Si2 atom,respectively.

The mechanical stability of a material is determined by its elastic properties. For the orthorhombic phase,there are nineindependent elastic constants:C11,C22,C33,C44,C55,C66,C12,C13, andC23. These elastic constants ofo-Si32 are calculated and are listed in Table 1. The elastic constants of theI4/mmm-Si andc-Si are also listed in Table 1 for comparison.At 0 GPa,the elastic constants of the orthorhombic symmetry crystal should obey the generalized Born mechanical stability criterion as follows:[26,27]C11>0,C22>0,C33>0,C44>0,C55>0,C66>0,[C11+C22+C33+2(C12+C13+C23)]>0,(C11+C22−2C12)>0, (C11+C33−2C13)>0, and (C22+C33−2C23)>0.

From Table 1, it can be seen that the elastic constants under ambient pressure satisfy the Born mechanical stability criterion. In other words,the newo-Si32 structure is mechanically stable. Furthermore, it can be seen thatC11andC22ofI4/mmm-Si ando-Si32 are almost equal but are both smaller than those ofc-Si. However,the elastic constantC33ofo-Si32 is larger than that ofI4/mmm-Si, which indicates that theo-Si32 has a stronger compressive deformation capacity along thez-axis direction thanI4/mmm-Si.

Table 1. Calculated values of elastic constant Cij, bulk modulus B, shear modulus G,Young’s modulus E,Poisson’s ratio ν,B/G ratio,Eg (HSE06),and Eg (PBE)of I4/mmm-Si,o-Si32,and c−Si.

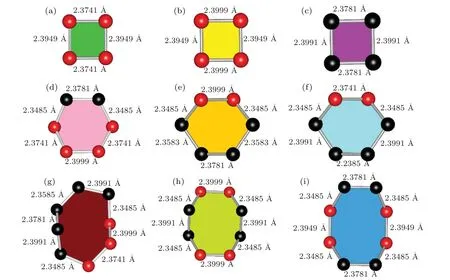
Fig.2. Silicon rings in o-Si32 structure,indicating((a),(b))two zigzag Si4 rings are composed of Si1 atoms,(c)zigzag Si4 ring is composed of Si2 atoms,((d)—(f))three Si6 rings are all composed of Si1 and Si2 atoms with different bond lengths,and((g)—(i))three zigzag Si8 rings are all also composed of Si1 and Si2 atoms with different bond lengths.

The elastic modulus is an important metric to measure the extent of elastic deformation of a structure. It can reflect the bonding strength of atoms,ions,or molecules in the structure from a microscale point of view. In general, the larger the elastic modulus,the larger the stiffness of the structure is. The bulk modulus (B) and shear modulus (E) ofo-Si32 are calculated according to the Voigt—Reuss—Hill approximation,[28]and the results are listed in Table 1. For the convenience of comparison, the moduli ofI4/mmm-Si, andc-Si are also listed in Table 1. The Young’s modulus(E)and Poisson’s ratio (ν) can be calculated from the following formulas:[29,30]E=9BG/(3B+G)andν=(3B−2G)/[2(3B+G)]. Both the bulk modulus and shear modulus ofo-Si32 are slightly larger than those ofI4/mmm-Si, whereas the Young’s modulus ofo-Si32 is slightly larger than that ofI4/mmm-Si. Pugh proposed that theB/Gratio can be used as a means to determine brittleness or ductility of a crystal.[31]AB/Gratio larger than 1.75 indicates a crystal with good ductility;on the contrary,aratio less than 1.75 implies a brittle crystal. Foro-Si32, the ratio ofB/Gis 3.94,which is larger than that ofI4/mmm-Si,indicating its high ductility. According to Frantsevich’s rule,a crystal shows brittleness(ductility)when its Poisson’s ratio is less than(larger than)1/3.[32]The Poisson’s ratio ofo-Si32 is 0.383 and thus indicates that the allotrope is ductile.

The phonon spectra ofo-Si32 are calculated to verify its structural stability,and the corresponding results are illustrated in Fig. 3. No imaginary frequency can be observed in the whole Brillouin zone; thus, it can be concluded thato-Si32 is dynamically stable. The thermodynamic stability ofo-Si32 is examined by a direct enthalpy comparison with previously reported silicon allotropes,and the results are shown in Fig.4.Figure 4 shows that theo-Si32 is energetically more favorable thanIm-3mandI4/mmmsilicon allotropes, confirming its thermodynamic stability.

Fig.3. Phonon spectra of o-Si32.

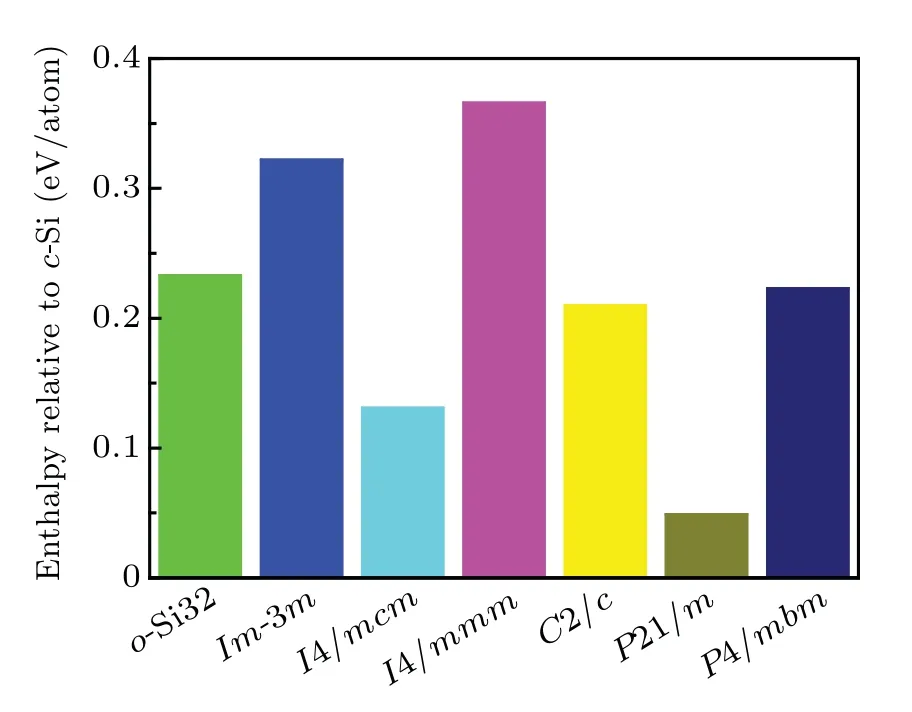
Fig.4. Enthalpy relative to c-Si of o-Si32 and other direct band silicon allotropes.

Atoms arrange with different periodicities and densities along different directions of a crystal, which results in different physical and chemical properties for different orientations; in other words, these crystals exhibit anisotropy. As is well known, elastic anisotropy plays an important role in engineering science and crystal physics. Describing the anisotropy behavior of the elasticity of a crystal by using the Young’s modulus graph of its three-dimensional (3D) surface is a feasible and effective method. For orthorhombic systems, the variation of Young’s modulus along an arbitrary [hkl] direction can be calculated as follows:[33]E−1=α4S11+β4S22+γ4S33+2α2β2S12+2α2γ2S13+2β2γ2S23+α2β2S66+α2γ2S55+β2γ2S44, whereα,β, andγare the direction cosines of the tensile stress direction, andSijare the elastic compliance constants. The result of this calculation foro-Si32 is presented in Fig.5(a),and the two-dimensional representations of Young’s modulus in thexy-plane,xz-plane,andyz-plane are illustrated in Fig. 5(b). As shown in Fig. 5(a),the structure exhibits anisotropy. In particular,it exhibits high anisotropy according to the extent of deviation from a sphere on the surface of the 3D model. Figure 5(b) shows that the anisotropy of Young’s modulus is mainly projected onto thexy-plane andxz-plane, relative to theyz-plane. Foro-Si32,the maximum(Emax)and minimum(Emin)of Young’s modulus are 98.8 GPa and 23.5 GPa, respectively, with an average value being 60 GPa. The ratio ofEmax/Eminis 4.20, which further suggests the existence of elastic anisotropy foro-Si32.

Fig. 5. (a) Young’s modulus in arbitrary direction for o-Si32; (b) Young’s modulus for o-Si32 projected onto xy-plane(black line),xz-plane(red line),and yz-plane(blue line).

The electronic properties of o-Si32 are calculated. Interestingly,o-Si32 is a direct semiconductor with a band gap of 0.682 eV at the PBE level. Foro-Si32,the valence band maximum and conduction band minimum are both located at theG point. Given that the band gap calculated by PBE is usually underestimated, the actual band gap is typically larger than the calculated result.[34]To address this problem, Heydet al.[23,24]proposed the Heyd—Scuseria—Ernzerhof (HSE06)functional, which is a more tractable hybrid functional approach. The expression of HSE06 is, where the HF mixing parameterµand the screening parameterωwith good accuracy for the band gap are 0.25−1and 0.207−1,respectively.[35]The band gap ofo-Si32 is calculated,and the band gaps ofI4/mmm-Si andc-Si are listed in Table 1. The band structure ofo-Si32 is shown in Fig. 6. From Table 1,it can be seen that the band gap ofo-Si32 is 1.261 eV at the HSE06 level. As shown in Fig. 7, the band structure ofc-Si has a band gap of 1.191 eV at HSE06 level,and theo-Si32 is a direct semiconductor,so it may have good optical properties.

Fig.6. Electronic band structure for o-Si32 at(a)PBE level and(b)HSE06 level.

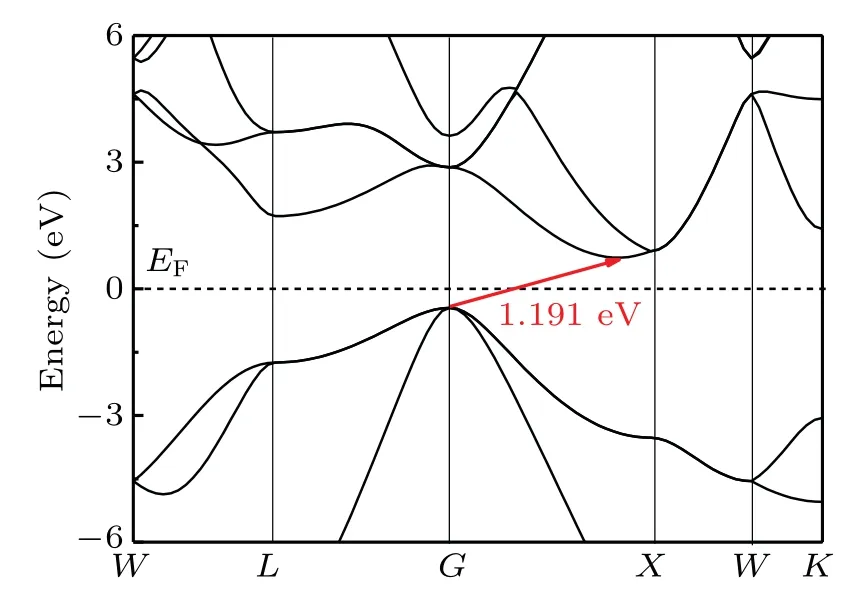
Fig.7. Electronic band structure for c-Si at HSE06 level.

In addition,we calculated the total density of states ofo-Si32 and the density of states projected onto some Si atoms,as shown in Fig.8. It can be seen from Fig.8 that theo-Si32 has the following two main characteristics:first,the main contribution of the state density at the peak of the low-energy part(−13 eV to−6 eV)comes from the electrons in the s orbital of silicon atom, while the contribution of the electrons in the p orbital is very small; second, the main contribution of the state density in the low energy part (−6 eV to 0 eV) and the high energy part (0 eV to 5 eV) comes from the electrons in the p orbital of the silicon atom,while the contribution of the electrons in the s orbital is very small.

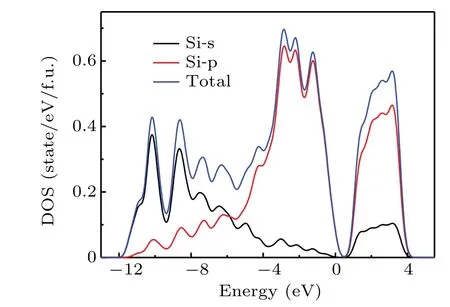
Fig.8. Densities of states for o-Si32.

4. Conclusions

In this work, we systematically study the structural and electronic properties ofo-Si32 based on first-principles calculations. From the results obtained for the elastic constants it is found thato-Si32 has a strong capability of compressive deformation along thezaxis. The Poisson’s ratio, the ratio of bulk modulus to shear modulus,and the directional dependence of Young’s modulus indicate that theo-Si32 exhibits ductility and good elastic anisotropy. In addition, the electronic band structure is calculated, revealing thato-Si32 is a direct semiconductor material with a band gap of 1.261 eV.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11965005 and 11964026), the 111 Project, China (Grant No. B17035), the Natural Science Basic Research Plan in Shaanxi Province of China(Grant Nos. 2020JM-186 and 2020JM-621), and the Fundamental Research Funds for the Central Universities,China.

All the authors thank the High Performance Computing Center of Xidian University for providing the computing facilities.