Determine the physical mechanism and source region of beat wave modulation by changing the frequency of high-frequency waves

Zhe Guo(郭哲), Hanxian Fang(方涵先),†, and Farideh Honary

1College of Meteorology and Oceanography,National University of Defense Technology,Changsha 410073,China

2Department of Physics,Lancaster University,Lancaster,LA1 4YB,UK

This paper introduces a new approach for the determination of the source region of beat wave(BW)modulation.This type of modulation is achieved by transmitting high-frequency(HF)continuous waves with a frequency difference f,where f is the frequency of modulated ELF/VLF(extremely low frequency/very low frequency)waves from two sub-arrays of a high power HF transmitter.Despite the advantages of BW modulation in terms of generating more stable ELF/VLF signal and high modulation efficiency, there exists a controversy on the physical mechanism of BW and its source region.In this paper, the two controversial theories, i.e., BW based on D-E region thermal nonlinearity and BW based on F region ponderomotive nonlinearity are examined for cases where each of these two theories exists exclusively or both of them exist simultaneously.According to the analysis and simulation results presented in this paper,it is found that the generated VLF signal amplitude exhibits significant variation as a function of HF frequency in different source regions.Therefore,this characteristic can be utilized as a potential new approach to determine the physical mechanism and source location of BW.

Keywords: powerful HF waves,ionospheric modulated heating,beat wave modulation,ELF/VLF waves

1.Introduction

The extremely low frequency/very low frequency(ELF/VLF) wave has important applications in navigation,submarine communication and detection of underground targets because of its strong penetration and weak attenuation for long distance propagation.Besides, high-energy electrons in the natural or artificial (such as high-altitude nuclear explosions) radiation belts can be precipitated through the process of wave-particle interaction with ELF/VLF waves,which is of great importance to protect astronauts and spacecrafts operating in these regions.However, the construction of ELF/VLF antenna arrays requires very large ground and high cost of maintenance.In addition, these arrays suffer from poor flexibility and low radiation efficiency.[1,2]To overcome these issues, an alternative approach has been adopted known as “ionospheric modulated heating”.

The so-called ionospheric modulated heating refers to the process of heating the local ionosphere with high-power highfrequency (HF) radio waves, causing the variation of some plasma parameters,so as to form a virtual antenna in the ionosphere to radiate ELF/VLF waves.The first feasible operation method of ionospheric modulated heating,amplitude modulation (AM), was proposed by Willis and Davis[3]and verified experimentally.[4]Its basic principle is that the high power HF transmitter,“heater”,is switched on and off with the expected ELF/VLF frequency, giving rise to an increase and decrease of local electron temperature with the modulation frequency,and such periodic change of electron temperature will cause the corresponding change of electron density and conductivity.This will provide periodic changes in the ionospheric current and results in radiating ELF/VLF waves.

The principle and operation of amplitude modulation is simple, but there are several limitations: 1) low modulation efficiency,2)dependence on electrojet and 3)poor signal quality.In order to overcome these problems,scientists have proposed and verified a number of other modulation methods as well as continuous upgrading of the ionospheric heating facilities over the past 40 years.

Some modulation methods are essentially modified ones based on AM, such as beam painting,[5]geometric modulation,[6]preheating-AM[7]and dual-beam HF modulation.[8]These methods improve the modulation efficiency to a certain extent, but just like AM, they also have the limitation of electrojet dependency.Some other electrojetindependent modulation methods,such as thermal cubic nonlinearity modulation,[9]ionospheric current drive,[10]lower hybrid(LH)-to-whistler mode conversion,[11]extend the time and range of latitude of ionospheric modulated heating.This paper is focused on beat wave (BW) modulation[12,13]which is achieved by transmitting HF continuous waves with a frequency differencef(fis the frequency of modulated ELF/VLF waves)from two sub-arrays of a heater.BW has the advantages of more stable ELF/VLF signal generation[14,15]and high modulation efficiency in higher VLF range.[16,17]However,it is not clear whether it is an electrojet-independent modulation method or not due to the controversy of its mechanism and source region of modulated ELF/VLF waves.For example,according to Refs.[17–23]the mechanism of BW is essentially the same as AM(i.e.,thermal nonlinearity),which means BW is an electrojet-dependent modulation method whose source region is located in the D-E region.Whereas Refs.[16,24–28] report that BW is an electrojet-independent modulation method,and the source region and mechanism of BW are F region ponderomotive nonlinearity.

In this paper, BW modulation efficiency as a function of HF frequency is simulated for two competing scenarios.In addition, since the possibility of combined action of the two theories exists according to Refs.[13,29],the effect of the superposition of the two theories is also explored by using the retarded potential method.

By comparing the simulation results, it is found that responses of BW based on different theories(including the combined action of two theories) to different HF frequencies are significantly different.This feature provides a new idea to determine the physical mechanism and source region of BW.

2.Physical model

As mentioned in the above section,there are two theories of BW: the first is BW based on thermal nonlinearity, whose source region is located in the D-E layer.The second is BW based on ponderomotive nonlinearity, whose source region is located in the F layer.In this section,the governing equations for these two theories are presented.For the case that both these theories exist simultaneously,the calculation method of superimposed magnetic field utilizing the retarded potential method is reported.

2.1.BW in the D-E region

The essence of BW in the D-E region is to periodically change the electron temperature in the D-E region in the process of modulated heating.This will lead to periodic changes in ionospheric conductivity at the same frequency.Hence, in the presence of ionospheric electric field,the ionospheric current is also modulated, causing the generation of the corresponding ELF/VLF waves.

The change of electron temperature during the modulated heating process can be represented by the energy equation[30]

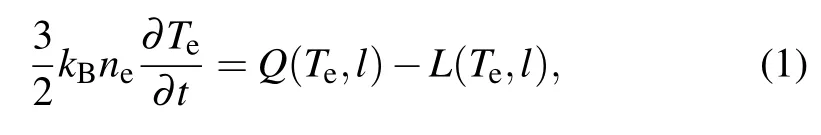
wherekBis the Boltzmann constant,neandTeare the electron density and temperature,respectively.L(Te,l)is the loss term of electronic energy.The absorption rateQ(Te,l)is given by[30]

where the energy fluxSof the HF wave is[30]

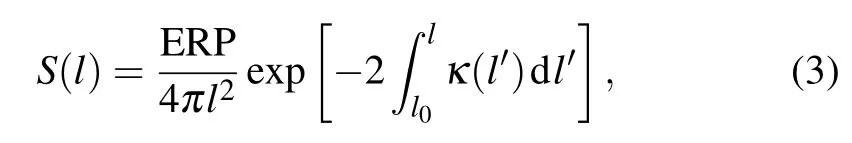
whilelis the altitude, ERP represents the effective radiated power,and κ is the absorption coefficient[30]

where ω0is the angular frequency of the HF wave,cis the speed of light and χ is the imaginary part of the complex refraction index.

As mentioned above, during the BW process, two subarrays of the heater transmit HF continuous waves with a frequency differencefin the ELF/VLF range, wherefis the beat wave frequency.The electric field of the total HF heater is given by[13]

where “±” represent O-mode and X-mode waves, respectively.Ep0is the amplitude of each HF wave.ω =2πfand ψ is the phase difference between the two HF waves.ω0andk0are the heater radian frequency and wave number,respectively.

The loss of electron energy in the ionosphere is dominated by collisions, this process is very complex, mainly including (1) elastic collision of electrons with positive ions;(2)elastic collision of electrons with neutral particles;(3)the excitation of the rotational level of O2and N2;(4)the excitation of the vibration level of O2and N2;and(5)the excitation of electronic energy level and fine structure of atom O.Detailed expressions are given by Ref.[31].

The electron density is determined from the continuity equation[32]

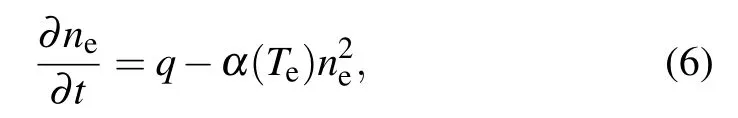
whereqis production rate and α(Te)is recombination coefficient.In the lower ionosphere, the molecular ions (NO+and)dominate the recombination process,so α(Te)can be calculated by[32]

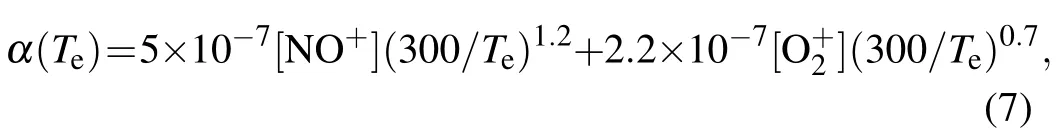
where[X]represents the density of particleX.The diffusion effect of the electron is ignored during the modulated heating process.

The electron temperature and density do not change synchronously during the process of BW in the D-E region: the time constant of the electron temperature is of the order of 0.01–1 ms,[7,30]while the time constant of the electron density is of the order of one minute.[7]In this paper, we focus on stimulating ELF/VLF waves with a frequency greater than 1 kHz,which means the modulation period is less than 1 ms,so the change of electron density is negligible during the modulated heating process.

The ionospheric current is[33]

whereE0=25 mV/m is the natural electric field.Two components of the ionospheric conductivity σ need to be considered in the modulated heating process,and they are Pedersen conductivity σPand Hall conductivity σH[21]

whereeis electron charge,Bis geomagnetic field, υenis the collision frequency between electrons and neutral particles,υinis the collision frequency between ions and neutral particles, ωeand ωiare the gyrofrequency of electron and ions,respectively.

Therefore, the periodic variation of ionospheric conductivity during the modulated heating process causes the periodic variation of ionospheric current.The vector potential is given by[7]

whereµ0is the permeability of free space andris the distance between a pointxin the heating region and a point in space.Thus,the magnetic field generated by the current is

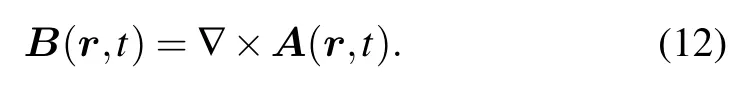
2.2.BW in the F region

According to the conclusion of Ref.[16], the ratio of thermal nonlinearity to ponderomotive nonlinearity during the process of BW in the F region is approximately equal to 4υe/3ω ≪1, where υeis the electron elastic collision frequency and ω is the modulated angular frequency.Therefore,in this paper, only the ponderomotive nonlinearity is considered during the process of BW in the F region.

The density of nonlinear beating current of these two HF waves is given by[13]

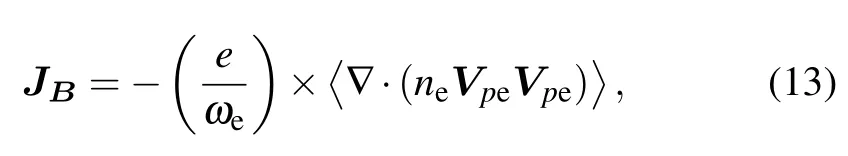
where Vpeis the electron velocity induced by the HF waves and〈〉represents a VLF bandpass filter.

The Vpeis given by[13]

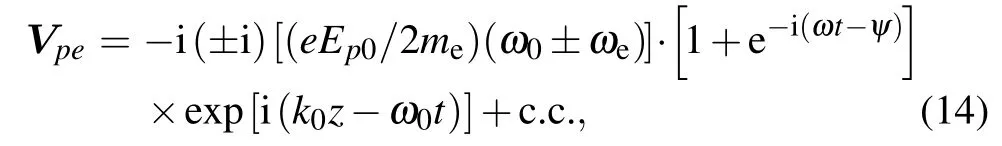
wheremeis electronic mass.

Substituting Eq.(14)into Eq.(13)gives

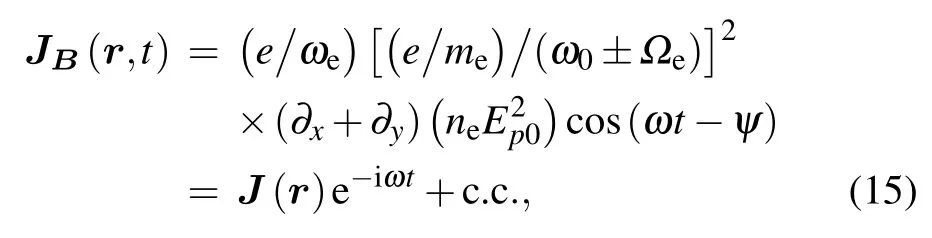
where

The phasor function of the vector potential of the ELF/VLF radiation is given by[13]

wherekis the wave number of the ELF/VLF wave.

Finally, the magnetic field of the modulated ELF/VLF wave is given by[13]

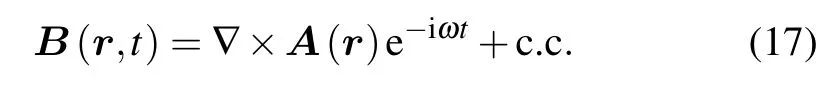
2.3.Superposition of BW in both D-E region and F region

According to superposition principle of magnetic field,the total magnetic fields of ELF/VLF waves is the vector sum of magnetic fields of ELF/VLF waves generated by BW in two source regions (as obtained according to physical models established in Subsections 2.1 and 2.2,respectively).The physical models in Subsections 2.1 and 2.2 have taken into account the retarded effect of the ELF/VLF wave generated by the BW in the respective source region, i.e., the ELF/VLF wave has phase delay when propagating from source region to field point.Just considering physical models,on the ground directly below source regions,the phase difference between magnetic fields of ELF/VLF waves generated by BW in two source regions iskd,wherekis the wave number of the ELF/VLF wave,anddis the distance between these two source region.But it is worth noting that,when calculating the superimposed magnetic field of ELF/VLF waves generated in two source regions,it is also necessary to take into account the time difference between HF waves propagation upward through these two source regions, in other words, the start time of BW in two source regions is different.Therefore, when calculating the superimposed magnetic field on the ground directly below source regions,the actual phase difference should be 2kd.

The simulation results in this paper are the magnetic field amplitudes of ELF/VLF waves received on the ground directly below the modulated heating source region.Therefore,the superimposed magnetic field of BW in the two source regions can be calculated by multiplyingr/candkrin Eqs.(11) and(16)by 2 respectively,remaining the rest unchanged and carrying out the vector sum.

3.Results and discussion

In this section, simulations of magnetic field amplitudes of 1)BW in the D-E region,2)BW in the F region and 3)superposition of BW in both D-E and F region received on the ground directly below the modulated heating source regions are presented (Physical models in Section 2 have been validated in Ref.[34]).Parameters of background ionosphere and atmosphere are chosen for 19 April 2015, 0600 UT, which were obtained by IRI-2016 and NRLMSISE-00 and the location of the HF transmitter is chosen as HAARP Facility(62.4°N,145°W).Figure 1 shows the variation of background ionospheric plasma frequency with height, as shown in the figure, the critical frequency of E and F layer are foE =0.915 MHz and foF2=5.15 MHz,respectively,and it is calculated that fxF2=5.87 MHz.

Fig.1.Variation of background ionospheric plasma frequency with altitude.

The modulation frequency is 5000 Hz.O-mode and Xmode HF waves are transmitted respectively,as shown in Table 1,the frequency of HF waves varies from 4.75 MHz(lower than foF2)to 6.25 MHz(higher than fxF2), which means the overdense and underdense cases of O-mode and X-mode are all included.Since we only focus on the variation of BW modulation efficiency with HF frequency in this paper,the gain of each HF frequency is fixed which means the beam width is fixed and the effective radiated power(ERP)is 150 MW for a single array.

Table 1.The frequency of HF waves and the corresponding type of heating(“1” represents overdense heating,and “0” represents underdense heating).

3.1.BW only existing in the D-E region

When only D-E layer BW is considered, it can be seen from Fig.2 that the radiation amplitude received on the ground uniformly decreases with an increase of HF frequency.This is mainly because as the frequency of HF waves increases,it is easier for HF waves to penetrate the lower ionosphere,and more of the wave energy will enter the F layer, so the amount of radio energy absorbed for heating the lower ionosphere gradually decreases.

In addition, the modulation efficiency of the X-mode wave is obviously higher than that of the O-mode wave at each incident HF frequency, and this is because for lower ionosphere, it is easier for X-mode waves to transfer energy to electrons than O-mode waves causing more disturbance of electron temperature,which can be verified by calculating the absorption termQ(Te,l)in Eq.(1).This is consistent with the experimental results.[35]However,it also means that X-mode waves of the same HF frequency have less energy entering the F layer than O-mode waves as more energy is lost in the lower ionosphere.This has an impact on the effect of BW in the F region,which will be discussed in the next section.

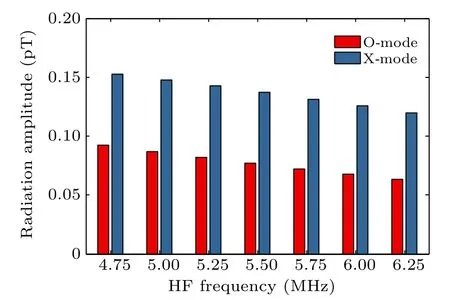
Fig.2.The amplitude of the VLF wave (f =5000 Hz) generated by BW in the D-E region of both O-mode waves and X-mode waves varies with the HF frequency.

3.2.BW only existing in the F region

It can be seen from Fig.3 that the variation of the efficiency of BW in the F region with HF frequency is more complex than that of D-E region,which is mainly reflected in three aspects:

1) In the case of overdense BW heating, O-mode waves are more efficient than X-mode waves of the same frequency,which is different from the conclusion in Ref.[13].According to Eq.(15), when other conditions (ERP, HF frequency,reflection height)are the same,the ratio of beat current generated by the X-mode wave and O-mode wave in the F region is[(ω0+ωe)/(ω0−ωe)]2,which means that the X-mode wave is more efficient than the O-mode wave,but it should be noted that the ratio decreases with an increase of the HF frequency(the HF frequency in Ref.[13] is 3.2 MHz, correspondingly,the ratio is about 6.53; however, in this paper, the ratio is only about 2.5–3).In addition,since X-mode waves are more strongly affected by D-E region absorption compared to Omode waves of the same frequency (with the HF frequency increases from 4.75 MHz to 6.25 MHz,the energy attenuation of O-mode waves and X-mode waves caused by D-E region absorption are 15%–10% and 42%–23%, respectively), less energy of X-mode waves reaches the F region.Finally,the Xmode wave is reflected below the O-mode wave of the same frequency,which means a smaller interaction region for modulated heating.Affected by the above factors, the amplitude of VLF waves modulated by the O-mode wave is higher than that of the X-mode wave as shown in Fig.3.

2)In the case of overdense heating,both the wave energy reaching the F region and the area of BW interaction region increase with the increase of HF frequency, but at the same time, the beating current decreases with the increase of HF frequency.As a result, the variation of modulation efficiency with HF frequency is uncertain.

3)The modulation efficiency of both O-mode waves and X-mode waves will be greatly reduced when the process of modulated heating changes from overdense heating to underdense heating with the increase of HF frequency.However,since fxF2 is higher than foF2, the modulation efficiency of the X-mode wave is much higher than that of the O-mode wave when the HF frequency is in the range between foF2 and fxF2 as shown in Fig.3.Only if the HF frequency continues to increase to above fxF2, then both X-mode and O-mode waves are produce underdense heating.Under this condition,the efficiency of BW modulation by the two mode waves can reach the same order of magnitude.

Furthermore,according to 2)and 3),the modulated VLF radiation is stronger when the HF waves were reflected in the region not too far below the foF2 layer rather than well below the foF2 layer,while the VLF radiation of underdense situation is weakest.This is consistent with the conclusion of Ref.[28].

Fig.3.The amplitude of the VLF wave (f =5000 Hz) generated by BW in the F region of both O-mode waves and X-mode waves varies with the HF frequency.The type of heating (overdense or underdense) at different frequency is shown in Table 1.

3.3.BW existing in both D-E and F region

The total amplitude of the VLF wave received on the ground when BW modulation in both D-E and F region are considered is presented in Fig.4.As can be seen from this figure, for the O-mode wave modulation, the superimposed amplitude of VLF waves is lower than the amplitude of VLF waves generated in the D-E or F region alone when the HF frequencies are 4.75 MHz and 5 MHz.On the other hand,for the X-mode wave modulation, when the HF frequency is within the range of 4.75–5.75 MHz, the superimposed amplitude of VLF waves exhibits both the case of between the amplitude of VLF waves generated in two source regions and the case of higher than the amplitude of VLF waves generated in each of the two source regions alone.Moreover, the amplitude of VLF waves is no longer monotonous with the increase of HF frequency,but fluctuates.This behavior is caused by the phase difference between the two source regions at different HF frequencies under the premise of conforming to the law of wave interference.In the frequency range of underdense heating in the F layer,the superimposed amplitude of VLF waves is basically the same as the amplitude of VLF waves generated by BW in the D-E region, and this is because the amplitude of VLF waves generated by BW in the F region is much lower than in the D-E region.

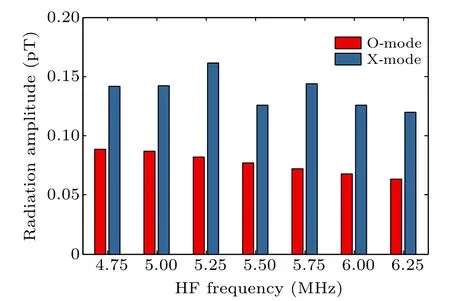
Fig.4.The superimposed amplitude of the VLF wave(f =5000 Hz)generated by BW in the D-E and F region of both O-mode waves and X-mode waves varies with the HF frequency.The type of heating(overdense or underdense)in F layer at different frequency is shown in Table 1.

4.Summary and conclusion

For BW in the D-E region, the modulation effect of Xmode waves is higher than O-mode waves under the same condition.Theoretically,the same conclusion is true for BW in the F region, but when the lower ionosphere is strong, the effect of D-E region absorption of X-mode waves is stronger than that of O-mode waves, so that less energy of X-mode waves reaches the F layer.In addition, the reflection height of Xmode waves is lower than that of O-mode waves at the same frequency, which means a smaller interaction region.In contrast to previously reported that BW by X-mode waves must be more effective than by O-mode waves,[13]this work illustrates that O-mode waves may have a better modulation efficiency in some cases.

The variation of the amplitude of VLF waves with HF frequency(mainly around foF2 and fxF2)is significantly different when the position of BW source region is different.

1) For BW in the D-E region, the modulation efficiency decreases uniformly and monotonically with the increase of the HF frequency,since HF waves can penetrate the D-E layer.

2)For BW in the F region,in the case of overdense heating, as the HF frequency increases, firstly, the energy of HF waves that can reach the F layer increases; secondly, the increase of the reflection height of HF waves increases the area of interaction region of BW,however, the beating current decreases during this process, therefore, the variation of modulation efficiency with the HF frequency is uncertain and needs to be analyzed according to the specific situation.When the HF frequency increases to the range of underdense heating,the modulation efficiency will decrease significantly compared with that of the overdense heating due to the disappearance of the swelling effect of HF electric field.

3)For BW existing in both D-E and F region,in the frequency range of F layer overdense heating, the amplitude of VLF waves fluctuates with the increase of HF frequency rather than monotonously change; in the frequency range of F layer underdense heating, the amplitude of VLF waves is basically the same as that of generated by BW in the D-E region,which means decreases with the increase of HF frequency.

In summary,the simulation results presented in this paper indicate that significant variation of the modulation efficiency of BW as a function of HF frequency exist in different source region.It has been shown that by changing the HF frequency(it should be noted here that the change of the HF frequency needs to cross the foF2 or fxF2 for O-mode waves or X-mode waves, respectively), and observing the variation trend of the amplitude of VLF waves received on the ground,the source region and the corresponding physical mechanism of BW can be determined.Therefore, changing the frequency of HF waves is a feasible and novel approach to solve the controversy of source region and mechanism of BW,although it still needs to be tested and verified by future experiments.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant No.41804149)and China Scholarship Council.