Experimental investigation on drag reduction in a turbulent boundary layer with a submerged synthetic jet

Biao-Hui Li(李彪辉) Kang-Jun Wang(王康俊) Yu-Fei Wang(王宇飞) and Nan Jiang(姜楠)

1Department of Mechanics,School of Mechanical Engineering,Tianjin University,Tianjin 300350,China2Key Laboratory of Modern Engineering Mechanics,Tianjin 300350,China

This work investigates the active control of a fully developed turbulent boundary layer by a submerged synthetic jet actuator. The impacts of the control are explored by measuring the streamwise velocities using particle image velocimetry,and reduction of the skin-friction drag is observed in a certain range downstream of the orifice. The coherent structure is defined and extracted using a spatial two-point correlation function, and it is found that the synthetic jet can efficiently reduce the streamwise scale of the coherent structure. Proper orthogonal decomposition analysis reveals that large-scale turbulent kinetic energy is significantly attenuated with the introduction of a synthetic jet. The conditional averaging results show that the induction effect of the prograde vortex on the low-speed fluid in a large-scale fluctuation velocity field is deadened,thereby suppressing the bursting process near the wall.

Keywords: synthetic jet,active control,turbulent boundary layer,drag reduction

1. Introduction

Despite the extensive amount of work accumulated over the years, turbulent boundary layer (TBL) control for reduction of skin friction is still a significant research topic owing to its great potential benefits.[1,2]Compared with passive control,[3–6]active control has better adaptability to complicated flow and can achieve an optimal control effect with a small energy input.[7–10]Among active control methods,steady blowing,[11]periodic blowing[12]and synthetic jets[13]can suppress the regeneration of the wall structure by weakening the burst of turbulence,thus reducing drag.

Chunget al.[14]computed the influence of wall blowing and suction on a fully developed,equilibrium turbulent channel flow through direct numerical simulation; they found that blowing makes the near-wall flow more isotropic. In contrast, under suction conditions, the anisotropy in the nearwall region is notably reinforced. Parket al.[15]experimentally probed the impact of periodic blowing and suction on the TBL using particle image velocimetry (PIV). Their results demonstrated that velocity retardation at the near-wall can bring about a decrease in skin friction under the action of blowing,and the attenuation of wall friction resistance was enhanced with increasing forcing frequency.

In recent years,the development of synthetic jet actuators(SJAs)has provided a novel means of applying drag reduction control for TBLs,[16,17]most importantly because they can impart extra momentum into the control region while injecting zero mass.[18,19]Adel Abbaset al.[20]summarized the state of the art of several technologies oriented to active control for turbulent drag reduction and pointed out that a SJA is one of the most crucial control modes. Guoet al.[21]introduced a local high-frequency perturbation to a flat-plate TBL with a synthetic jet;the disturbance gradually developed downstream of the slot and ultimately affected the near-wall regeneration mechanism of the turbulent structures. Yeet al.[22]adopted a synthetic jet array to modify the flow field structure in a TBL.Once the array was turned on,the near-wall structure was elevated,which thickened the viscous sublayer and reduced frictional resistance.

Previous studies have proved the feasibility and enormous potential of synthetic jets for the reduction of TBL drag;however, most of the relevant research has been carried out in wind tunnels.[23,24]Considering the current urgent need for underwater drag reduction control, we employed an active control scheme with a submerged SJA to disturb the flow field.Time-resolved particle image velocimetry(TR-PIV)was used to obtain quantitative measurements. The single-pixel ensemble correlation (SPEC) algorithm was utilized to accurately measure the velocity in the near-wall region to overcome the limitations of traditional PIV in calculating wall friction velocity.[25]Based on an assessment of the spatial characteristics of fluctuation velocity,the scale features of the flow were separated by proper orthogonal decomposition(POD);finally,conditional averaging was used to further reveal the influence of the synthetic jet.

2. Experimental setup and procedure

The experiments were carried out in a low-speed recirculating water channel at Tianjin University, as shown in Fig. 1(a). The size of the working section was 6200 mm×300 mm×380 mm (length×width×height) and the background turbulence intensity was estimated to be about 1.5%.A zero-pressure gradient boundary layer flow was developed along a smooth Plexiglas plate with dimensions of 2900 mm×294 mm×20 mm(length×width×thickness)and a 4:1 elliptical leading edge. The fully developed TBL was stimulated by a trip wire with a diameter of 2 mm at the plate 100 mm downstream of the leading edge. On the central line 2450 mm away from the leading edge of the plate, a 1-mm long and 10-mm wide hole was made in the test plate where the actuator was situated underneath to generate the synthetic jet, as illustrated in Fig.1(b). The signal of the SJA had a sinusoidal waveform with a voltage of 9 V,and an excitation frequency of 26 Hz. The coordinate axesx,y,andzdenote the streamwise,wall-normal, and spanwise directions, respectively, while the corresponding velocities are designated asu,v, andw. The center of the outlet of the synthetic jet in the streamwise direction is defined asx=0.

The TR-PIV system was used to measure the instantaneous velocity field. The fluid was seeded with polyamide particles with a mean diameter of 20µm and a specific gravity of 1.03 g/cm3.The measurement plane (x–yplane) was illuminated by a laser sheet with a light thickness of around 1mm. The investigations were conducted in two parts, including experiments on the characteristics of the synthetic jet and experiments on the interaction between the synthetic jet and the mainstream. When there was no flow, 8216 continuous snapshots of particle images were captured by camera#1 (which faced the center of the jet outlet) with a sampling frequency of 400 Hz; these were analyzed by adaptive correlation with interrogation windows of 32 pixels×32 pixels and an overlap rate of 75%. The field of view was nearly 60.21 mm×37.63 mm and the spatial distance per vector was 0.3763 mm. Once the inverter motor of the water channel had been activated and until the incoming flow stabilized,two CCD cameras with a resolution of 1280 pixels×800 pixels recorded 8216×4 images separately at the same time. For camera#1,Dynamic Studio software from Dance was utilized to remove noise and transform the particle images to the velocity field. The interrogation window for adaptive correlation was 32 pixels×32 pixels with a 75% overlap. Eventually,156×92 velocity vectors were reconstructed for each image with a vector pitch of 0.6248 mm. The pseudovector produced by the experimental data was below 1%. For camera#2, the measurement area was approximately 20 mm–50 mm downstream of the synthetic jet exit and the field of view was smaller(with the intention of achieving a higher resolution in the near-wall area and accurately calculating the skin friction velocity by means of SPEC).[26,27]The relative error of the skin friction velocity depends on the ensemble size of the image samples,and the relative error will be less than 0.1%when the ensemble size exceeds 2000.[27]Detailed experimental parameters are included in Table 1.

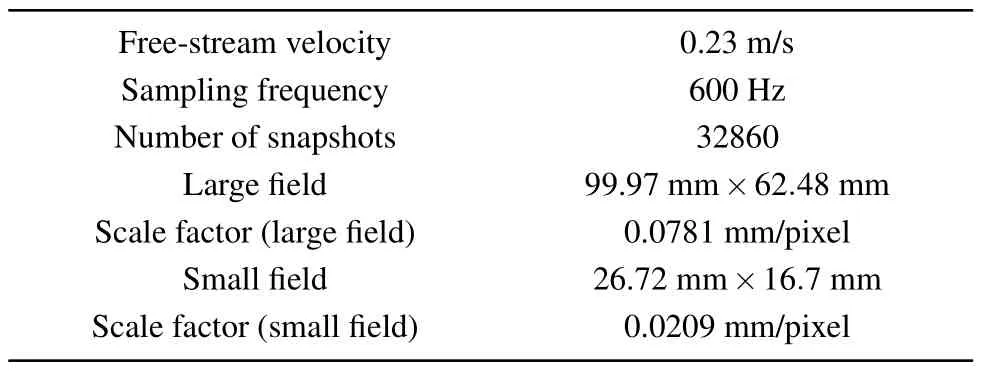
Table 1. Experimental parameters.

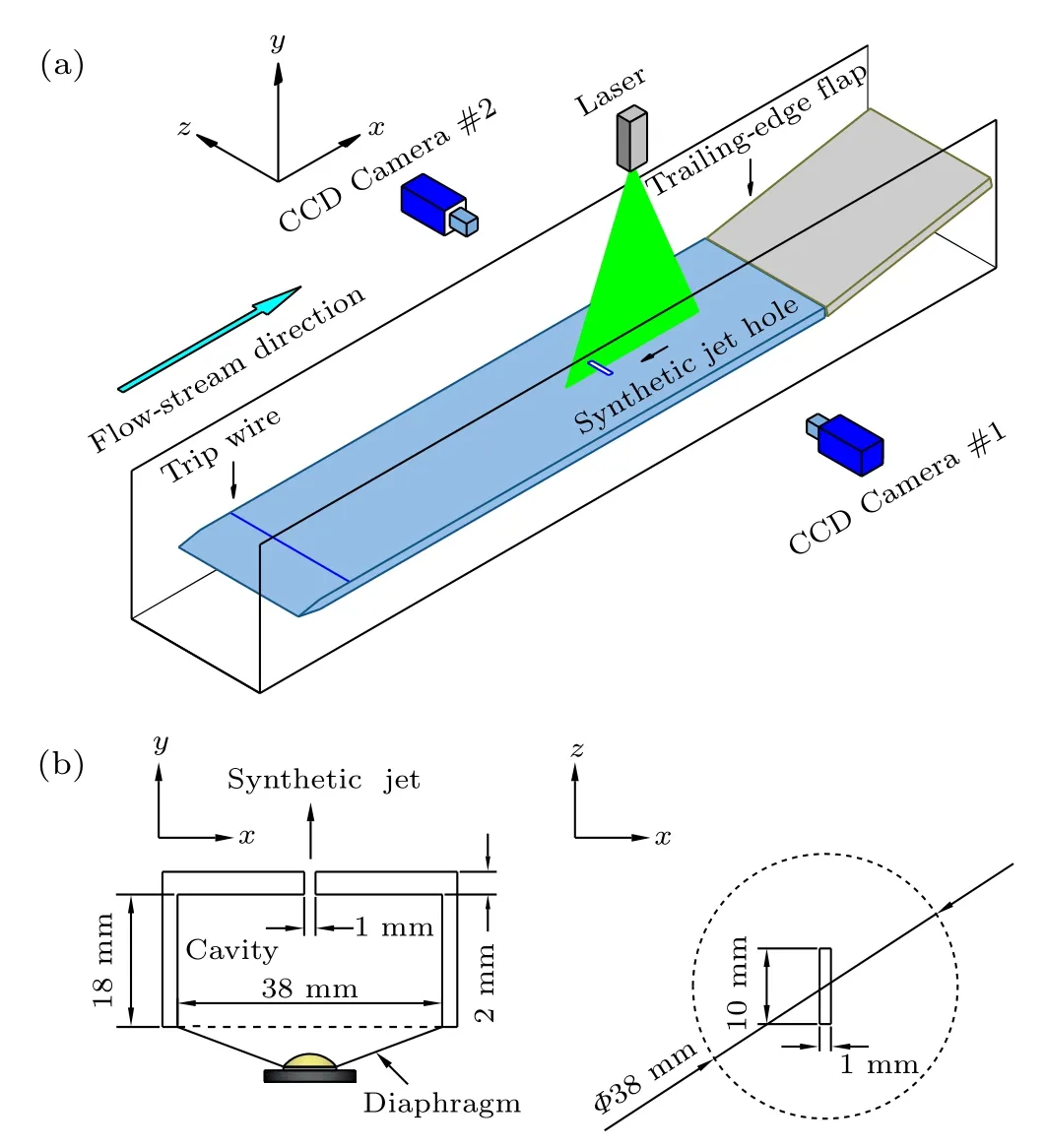
Fig. 1. Schematic diagram of the experimental setup: (a) the test platform;(b)the synthetic jet actuator.

3. Result and analysis

3.1. Characteristics of the synthetic jet

Figure 2(a)plots the time-averaged flow field of the synthetic jet. The coordinates have been normalized by the width of the jet openingd. Although the working process of the synthetic jet is divided into blowing and suction phases,[28]the periodic disturbance of the SJA exerts a similar impression to that of continuous blowing.The directionality of the flow field is single and stable,with only partial backflow near both sides of the exit. Therefore, it is concluded that the impact of the blowing phase on the external environment is greater than that of the suction phase. Meanwhile, the jet is mainly concentrated in the near field and has little effect on the far field. The synthetic jet centerline velocity is given in Fig.2(b). The maximum velocity appears at abouty/d=2.4, after which it decays rapidly and then slowly asy/dincreases.The above properties of the synthetic jet signify that it can be implemented in drag reduction control in a TBL.[29]

Fig.2. Characteristics of synthetic jet: (a)time-averaged flow field;(b)synthetic jet centerline velocity.

3.2. Turbulence statistics

Figure 3 compares the contours of the streamwise mean velocity field under different working conditions. When the fluid in the near-wall region flows over the jet outlet, a tiny bulge appears and the thickness of the downstream near-wall region increases while the velocity gradient decreases, leading to a reduction in skin-friction drag. In addition, the rise of the near-wall region caused by the synthetic jet reaches a maximum at 40 mm downstream of the exit, and then gradually reduces. It is estimated that the fluid field will eventually return to the state before the control was applied.

Fig. 3. Contours of the streamwise mean velocity field: (a) 0 V, 0 Hz; (b)9 V,26 Hz.

The basic flow parameters in the TBL in the different experiments are summarized in Table 2.U∞represents the main stream velocity,δis the thickness of the TBL andReτ=uτδ/νandReθ=U∞θ/νare Reynolds numbers based on the skin friction velocityuτand momentum thicknessθ,respectively.

As indicated in Fig.4(a),the outer-scale average velocity profiles of the viscous sublayer show good linear distribution and can be linearly fitted.[30]The wall shear stressτwcan be computed from the profile slope according to

Here, the density of waterρis 998 kg/m3and the kinematic viscosityνis 9.7×10−7m2/s. The skin friction velocityuτwill be obtained by the function

Then,the fictional factor is defined as follows:

so the drag reduction ratio DR can be expressed as

whereCf0andCf1denote the frictional coefficients before and after control is applied, respectively. As a result, the average percentage drag reduction 20 mm–50 mm downstream of the jet opening is 19.37%.

Table 2. Turbulent boundary layer properties for each condition.

In Fig.4(b),the mean velocity profiles are normalized by inner-scale unitsu+=u/uτ,y+=yuτ/ν. Overall,the log-law region has lifted up clearly in the presence of the synthetic jet,which is a typical feature of drag reduction in a TBL.[31,32]

Fig.4. Mean velocity profiles: (a)outer-scale;(b)inner-scale.

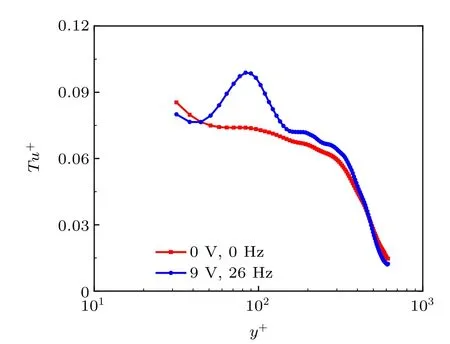
Fig.5. Comparison of streamwise turbulence intensity.

Figure 5 shows the contrasting profiles of streamwise turbulence intensityis the root mean square of streamwise fluctuating velocityu′). In the near-wall region ofy+<45,the controlledTu+is less than the uncontrolled value;this is caused by the uplift of the streamwise vortices under the effect of upwash restraining the interaction between the coherent structure and the wall.The controlled peak appears neary+=85. This dual-peak phenomenon has been corroborated by previous studies.[29,33]Additionally, in the process of moving along the streamwise and the wall-normal direction, the spanwise vortex generated by the synthetic jetcontinuously interacts with the surrounding fluid resulting in a large turbulence intensity,and the peak in theTu+profile can be considered as the center of the spanwise vortex.[29]After the peak, the synthetic jet gradually loses its influence on the flow field,andTu+finally shows a similar trend to the uncontrolled case.

3.3. Two-point correlation

Spatial two-point correlation involves a great deal of information regarding the average spatial structure in wall turbulence;[34,35]therefore,the impact of a synthetic jet on the underlying structure of the flow can be quantitatively explored by this method.The two-point velocity correlation coefficients are given by

where Δxis the spatial distance between two correlated points in the streamwise direction,σiandσjare root-mean squares of thei-th andj-th velocity components andyrefsignifies the reference wall-normal position.In this study,yref=0.15δ,which is close to the location of the peakTu+mentioned above.

Figures 6(a) and 6(b) present contours ofRuufor different cases. There is a certain similarity between theRuuas the streamwise scale is larger than the wall-normal scale. The difference is that the controlledRuuis farther away from the wall. Moreover,the inclination angle ofRuu,related to the average inclination of the hairpin packet, is distinctly greater in the controlled case. To quantify the angle, we used the leastsquares method[36]to fit the boundary points on the contours.Considering the regularity of the ellipse fitting, the reference value of the contour level was determined as 0.3. The inclination angles before and after control is utilized are 6.4°and 9.3°, respectively, suggesting that the vortex organization is greatly lifted under the action of the synthetic jet.

Quantitative characterization of the one-dimensional profiles ofRuuis displayed in Fig. 6(c). Evidently, the presence of a synthetic jet shortens the streamwise extentLxuu,which is defined as twice the streamwise distance between the correlation level of 0.5 and the self-correlation peak.[5]Lxuuis about 20% smaller for the controlled case, and it can be concluded that the synthetic jet has an inhibitory effect on the streamwise scale ofRuu.

Figures 7(a)and 7(b)give the contours ofRvvfor different cases. Compared withRuu,Rvvis considerably less elongated in the streamwise direction. With respect to the uncontrolled case,the contour ofRvvis slightly inclined to the upper right,while with the action of the SJA it is more perpendicular to the wall and flatter in outline, which can be regarded as the modulation in impact produced by the synthetic jet in the wallnormal direction during the blowing phase.

A quantitative contrast of the one-dimensional profiles ofRvvis presented in Fig.7(c). The streamwise extentLxvvhas the same definition asLxuu. At a correlation level of 0.5,Lxvvis around 13%lower than in the case without control,indicating that the synthetic jet also blocks the extension ofRvvin the streamwise direction.

Fig.6. Contours of spatial two-point correlation coefficients Ruu and one-dimensional profiles: (a)0 V,0 Hz;(b)9 V,26 Hz. (c)Streamwise extents.

Fig.7. Contours of spatial two-point correlation coefficients Rvv and one-dimensional profiles: (a)0 V,0 Hz;(b)9 V,26 Hz. (c)Streamwise extents.

3.4. Proper orthogonal decomposition analysis

As described in Subsection 3.3, it seems that the current synthetic jet has modified the streamwise coherence of bothRuuandRvv. Snapshot POD could be employed from the perspective of turbulent kinetic energy (TKE)[37,38]for the purpose of separating the scale features of flow. The specific process is as follows.

When therefore the thirteenth2 came into the world, he knew not what to do in his trouble, but ran out into the great highway, and resolved to ask the first person whom he met to be godfather

First,the fluctuating velocity field matrix is written as

Here,m=(u′,v′)and each column of the matrix corresponds to a moment and contains the two-component information about the fluctuating velocity at all spatial velocity measurement points. Then the spatial correlation matrix can be obtained as

whereMTis the transposed matrix ofM.Afterwards,we solve the eigenvalues and eigenvectors ofR

whereAiis the eigenvector and the eigenvalueλirepresents the TKE contribution of thei-th POD mode.

The basic function for the POD mode is expressed as

After the above calculation process,the POD mode can be realized as

Here,the random temporal functionan=φTmn.

Figure 8(a)refers to the fractional contributions of single POD modes to total TKE.For the first four modes,the proportion of energy after control is lower than with no control.Starting with the fifth mode, the result is reversed. That is to say,the application of the synthetic jet causes the low-order(largescale)energy to be weakened while enhancing the high-order(small-scale) energetic turbulent events. Figure 8(b) displays the distribution of cumulative energy. In the low-order mode range,the cumulative energy of the controlled flow field is obviously smaller than that of the uncontrolled field,whereas the two curves are relatively close from the 200th order on,showing that the more coherent small-scale structures are concentrated in the flow field when the synthetic jet exists.

The contours for the first-order POD mode in both conditions are shown in Fig.9. Since the POD is realized based on a statistical correlation function, the first-order mode can be seen as the average result of flow field pulsation. The contours have a similar distribution to the coherent structure acquired by spatial correlation. The controlled flow field is constantly regulated by the synthetic jet,which impedes the growth of a coherent structure in the flow direction and lifts the coherent structure away from the wall, thereby weakening the interaction between the coherent structure and the wall as the flow moves downstream.

Fig.8.POD spectrum energy distributions:(a)single energy distribution;(b)cumulative energy distribution.

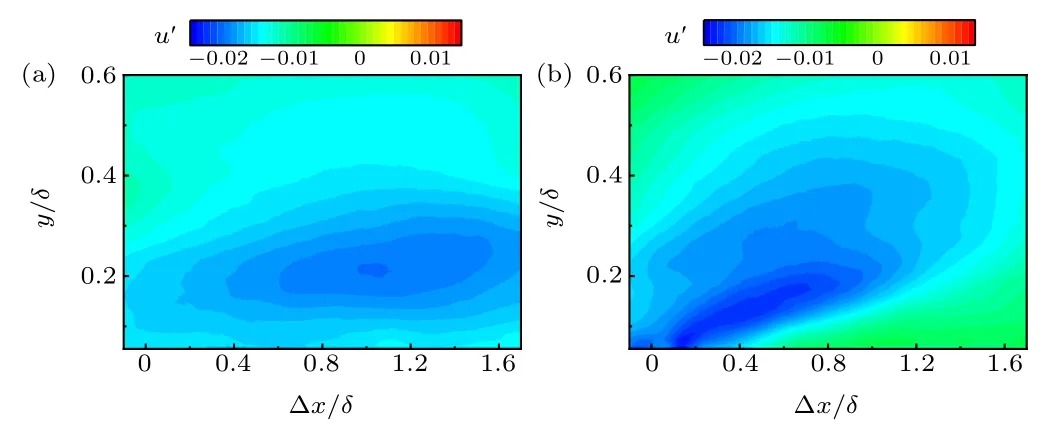
Fig.9. Contours for the first-order POD mode: (a)0 V,0 Hz;(b)9 V,26 Hz.

A low-order reconstruction of the leadingKPOD modes is taken to be

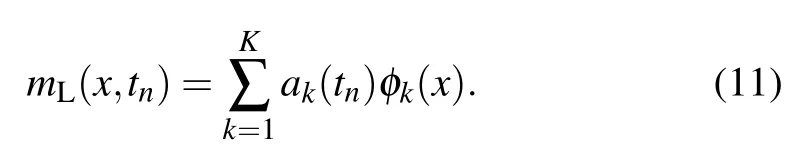
Consequently, the residual field, composed of the high-order modes,is given by

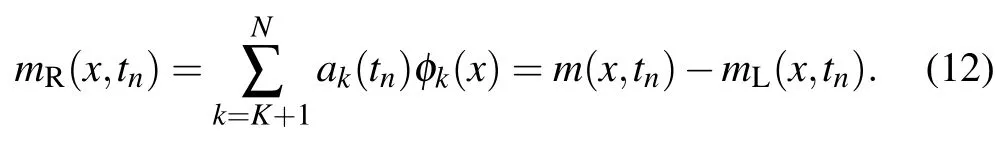
In this paper,the number of modes selected for reconstruction is the minimum number required to capture 80%of the TKE in the measurement area. Figure 10 displays the profiles ofTu+calculated from low-order (large-scale) and associated residual(small-scale)velocity fields. As can be seen from this figure,the trends of large-scaley+=45 and small-scale contribution toTu+are similar to the results of Wu and Christensen[39]in the case of no control. In Fig.10(a),the curve of large-scaleTu+is consistent with Fig.5,whereas the corresponding amplitudes decrease. Furthermore, the restraint of the synthetic jet on large-scaleTu+can reachy+=60, higher than that in Fig.5, and the peak position ofTu+remains unchanged. By comparison, as illustrated in Fig. 10(b), in the near-wall region the suppression on the small-scaleTu+by the syntheticjet is similar to that in Fig.5,and the peak position ofTu+isy+=65,closer to the wall;this is due to the small-scale spanwise vortex introduced by the synthetic jet. The above analysis of Figs.5 and 10 shows that the large-scale components ofTu+account for a relatively high proportion,and the synthetic jet shows more effective inhibition of these components.

Fig.10. Comparison of Tu+ from low-order and residual velocity fields: (a)low-order contribution;(b)residual contribution.

3.5. Conditional average

In order to identify the variation in large-and small-scale turbulent fluctuations and vortex structures the method of conditional averaging was implemented, based on spanwise vorticity as a conditional event. Theλcicriterion[40]was adopted for visualizing vortex structures using the following equation:

Here,λcistands for the imaginary part of the complex eigenvalue of the velocity gradient tensor andωis the spanwise vorticity. The specific expression for the detection function is defined as

whereandare the large and small-scaleu′,respectively,andyref=0.15δ. Since the coherent structure extracted by conditional detection conforms to the structural characteristics of a hairpin vortex, andΛci<0, the velocity fields after conditional averaging denote the average of the fluctuating velocities near the head of the hairpin vortex and the ejection event of low-speed fluid.[41]

The contours presented in Fig.11 are the conditional averages of the large-scale streamwise fluctuating velocity. As shown in Figs. 11(a) and 11(b), there is a strong clockwise rotating vortex in the detection center, and below it are lowspeed upward ejected fluids induced by the vortex. The tough shear between the prograde vortex and the wall is the main source of wall frictional resistance.[42]Before and after applying control,the positive fluctuation increases successively,although the negative fluctuation continues to decrease.This is attributed to the presence of the synthetic jet causing the prograde vortex to rise, thus impairing its inductive influence on the low-speed fluid,and the diminution of the induced region in the streamwise range is conducive to weakening the burstintensity of turbulence events in the near-wall. Beyond that,upstream of the vortex,the upward ejection of low-speed fluid fails because of interaction with the high-speed fluid sweeping downward,so that the fluid almost stagnates and forms a stagnation point (black point)[43]where violent Reynolds stress events occur. The regulatory effects of the synthetic jet on the mainstream lead to the stagnation point moving in the direction normal to the far wall,greatly lowering the momentum energy and mass transport ascribed to the Reynolds shear stress at the near wall and realizing the purpose of drag reduction.

Fig.11. Conditional average contours of : (a)0 V,0 Hz;(b)9 V,26 Hz.

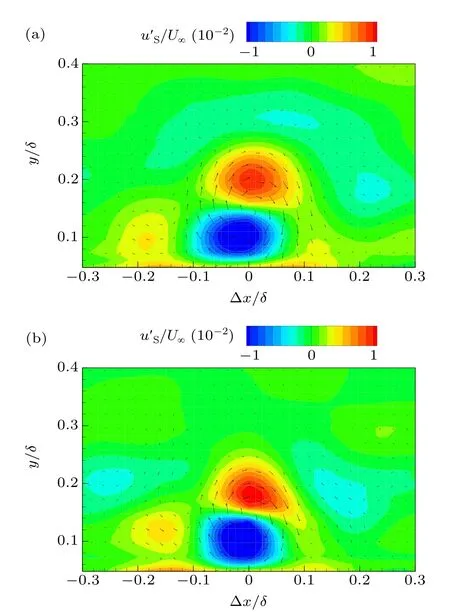
Fig.12. Conditional average contours of : (a)0 V,0 Hz;(b)9 V,26 Hz.

The conditional average contours of small-scale streamwise fluctuating velocity are plotted in Fig. 12. For the synthetic jet, the positive and negative small-scale fluctuations both increase slightly, and the position of the prograde vorticity is closer to the wall. The enhancement of small-scale fluctuation includes two aspects:one is that small-scale disturbance incessantly arises from the synthetic jet,and the other is dissipation of the large-scale structure related to wall friction by such a perturbation.

4. Conclusion

The characteristics of a submerged synthetic jet and its influence on the TBL were explored by TR-PIV technology.The following conclusions are presented.

(i)The blowing phase is dominant over the whole jet cycle;this exerts an effect similar to continuous blowing,suitable for active drag reduction control in the TBL.

(ii) In the near-wall region, the synthetic jet raises the streamwise vortices,Tu+is attenuated and an average drag reduction rate of 19.37%in the range of 20 mm–50 mm downstream of the opening is achieved.

(iii) Under the impact of upwash, the coherent structure is lifted and extension along the streamwise direction is hindered,resulting in a restraining of the interaction with the wall in the downstream region.

(iv) The synthetic jet significantly attenuates the largescale TKE related to the skin-friction drag in the flow field,so that the distribution of TKE is concentrated to a small-scale coherent structure.

(v) Introduction of the synthetic jet deadens the induction effect of the prograde vortex on the low-speed fluid in the large-scale fluctuation velocity field,and reduces the burst process of turbulence events near the wall,thus realizing drag reduction.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.11732010,11972251,11872272,11902218, and 11802195) and the National Key Research and Development Program of China,on‘Green Buildings and Building Industrialization’(Grant No.2018YFC0705300).