Explosive synchronization: From synthetic to real-world networks

Atiyeh Bayani, Sajad Jafari,2,†, and Hamed Azarnoush

1Department of Biomedical Engineering,Amirkabir University of Technology,No.350,Hafez Ave.,Valiasr Square,Tehran 159163-4311,Iran

2Health Technology Research Institute,Amirkabir University of Technology,No.350,Hafez Ave.,Valiasr Square,Tehran 159163-4311,Iran

Synchronization is a widespread phenomenon in both synthetic and real-world networks.This collective behavior of simple and complex systems has been attracting much research during the last decades.Two different routes to synchrony are defined in networks; first-order, characterized as explosive, and second-order, characterized as continuous transition.Although pioneer researches explained that the transition type is a generic feature in the networks,recent studies proposed some frameworks in which different phase and even chaotic oscillators exhibit explosive synchronization.The relationship between the structural properties of the network and the dynamical features of the oscillators is mainly proclaimed because some of these frameworks show abrupt transitions.Despite different theoretical analyses about the appearance of the firstorder transition,studies are limited to the mean-field theory,which cannot be generalized to all networks.There are different real-world and man-made networks whose properties can be characterized in terms of explosive synchronization,e.g.,the transition from unconsciousness to wakefulness in the brain and spontaneous synchronization of power-grid networks.In this review article, explosive synchronization is discussed from two main aspects.First, pioneer articles are categorized from the dynamical-structural framework point of view.Then,articles that considered different oscillators in the explosive synchronization frameworks are studied.In this article, the main focus is on the explosive synchronization in networks with chaotic and neuronal oscillators.Also, efforts have been made to consider the recent articles which proposed new frameworks of explosive synchronization.

Keywords: synchronization, explosive synchronization, Kuramoto oscillator, chaotic systems, neuronal networks,complex network

1.Introduction

Synchronization is generally known as the collective behavior of units that interact with each other.[1]The dynamics of units become relatively correlated as their coupling gets strong.Therefore,the coupling strength should pass a critical value specific to different networks with different structures and units’ dynamics.[2]Synchronization patterns are seen in natural and human-made systems,like fireflies,neurons,heart cells,pendulums,and lasers.[3]Besides the coherent state,another collective behavior is also desynchronization,[4]which may be induced or happen because of instability of the synchronization state.[5,6]

Analyzing the synchrony of the systems has gained much interest in different fields,like physics,[7,8]biology,[9,10]mechanics,[11]chemistry,[12,13]and even ecology,[14,15]in which network sizes vary significantly from two to millions of nodes.The research in these fields consists of analytical, numerical, and experimental studies which mainly investigate the required critical coupling strength,[16]external input,[17]control scheme,[18]network structure,[19,20]and agent parameters[21]to synchronize,desynchronize,and control the system.[1]

The history of synchronization goes back to 1665, when Christiaan Huygens, a mathematician, observed two pendulum clocks (invented by himself) move alongside each other.His study was the pioneer to further studies in which weakly sinusoidal coupled phase oscillators were analyzed using the mean-field theory in an all-to-all coupled network, the Kuramoto model (KM).[22]This model is the most popular and well-studied model to describe synchronization and related phenomena.The order parameter, the index which quantified the synchronization level, is easily calculated in this model via summation of the state variables on the unit circle.[23]Some complex conditions were discovered in Kuramoto networks for the first time,like chimera[24]and explosive synchronization.[25]The effect of different structures on the synchrony of Kuramoto networks is reviewed in Ref.[26],providing a good insight into this model’s applications.

Recent research generalizes the synchronization definition to chaotic systems.[27,28]Unlike phase oscillators, the term synchronization cannot be used for chaotic systems without additional information.It should be noted which synchrony is considered.In chaotic systems, the correlation between the properties of some correlated oscillators is characterized as synchrony.[28]For example, complete,[27]phase,[29]time-scale,[30]lag,[31]and generalized[32]synchronization.The chaotic systems have been widely investigated and used in communication,[33]physics,[34]mechanics,[35]and biological[36]fields.In some chaotic systems, the basin of attraction has different regions that correspond to an attractor.These systems are known as systems with multistability or coexisting attractors.[37–39]Studies show that multistability makes the networks show asynchronization even in large values of coupling strength.[40]

Besides the different types of synchrony,the transition to this state varies in different types of oscillators and network structures.Routes to the coherent state have been divided into two types; first-order transition,i.e., explosive synchronization (ES), and second-order transition,i.e., continuous transition.Studies show that forward (FW) and backward (BW)continuations of the order parameter as a function of the coupling strength have a hysteresis loop.In other words,the critical coupling strength from the incoherent state to coherent one,is different from the critical coupling strength,which is achieved from synchronization state to desynchronized one.[41]Two detailed reviews explain the pioneer articles of ES phenomena.[42,43]

As mentioned above,the Kuramoto oscillator is discussed well in the previous reviews.Thus,in this review(Section 2),in addition to explaining the pioneer studies(Subsections 2.1–2.5), the main focus is on the ES phenomenon in new frameworks(Subsection 2.6).In Section 3,the reasons for the emergence of ES are discussed.Different types of oscillators, focusing on chaotic and neuronal oscillators, are considered in Section 4.Moreover,recent applications of the first-order transition in real-world systems are considered in Section 5.Explosive death is discussed as an abrupt behavior of the networks in Section 6.Also, Section 7 includes the concluding remarks and the future outlook.

2.Explosive synchronization in different frameworks

Full rank all-to-all connected graphs have been used in physics and mathematics for a long time.The analytical study of this kind of network has been strengthened through meanfield theory and other investigations.Nevertheless,some studies show that this model is not perfectly compatible with nature networks.Arbitrary connections between the nodes make the networks more realistic but challenging to solve mathematically.These types of connection realizations provide a new category of networks which is demonstrated as complex networks.They range from regular to random structures in which the probability of the nodes’connection,i.e.,degree probability(P(k)),determines the network’s construction.[2]Although,networks can be classified using other features like the average shortest path length,l,or the clustering coefficient,C.

In the context of the ES, two different types of networks are always debated, which differ in the tail of the degree distribution diagram,namely,homogenous networks,for which the probability decays exponentially fast as the degree increases, and the heterogeneous networks, with the heavytailed distribution.Random, Erds–Rnyi (ER) as the most typical one,[44]and scale-free (SF) networks,e.g., Barabsi–Albert (BA),[45]are homogenous and heterogeneous, respectively.Another essential structure is the small-world (SW),constructed by adding some additional random links to a regular graph.Watts–Strogatz(WS)is an algorithm that generates networks with SW property.[46]

In the following subsections,the existence of ES in simple networks of the Kuramoto model is discussed.Then, the frameworks which consider the KM model in the complex networks are reviewed.It should be noted that this review’s focus is on those structures which have not been considered in the previous reviews.

2.1.Kuramoto networks

To describe the synchronization in phase oscillator, Kuramoto proposed a model in which the nonlinear sinus function describes the nodes’ coupling term.Recent advances in the study of Kuramoto networks are reviewed in Ref.[26].The phase derivative(˙θ)of nodei,in a network ofNoscillators,is described as

whereKis the coupling constant connecting the oscillators in an all-to-all network; ωiis the intrinsic frequency of theith oscillator,chosen from the frequency distribution function,g(ω).The term 1/Nlimits the coupling term whenN→∞(thermodynamic limit).

To calculate how much the oscillators are synchronized,the order parameter is computed in the networks.This parameter mostly ranges from 0 to 1,which shows full non-coherence and coherence states,respectively.The definition of order parameter differs in different types of oscillators.In phase oscillators,it is defined as the collective behavior of all the agents known as the global order parameterr,

where φ is the average phase.In the non-synchronized stater～～0 and in the synchronized one,it is approximately equal to 1.Figure 1 shows this index for(a)relatively synchronized and(b)incoherent states.

As mentioned before, abrupt synchronization was reported in the Kuramoto model for the first time in Ref.[25].Then, most studies focused on the role of frequency distribution in the appearance of ES.Uniform[47]and symmetric unimodal[48]distributions were analyzed, which yield ES.Hence, it seemed thatg(ω) should have a large flat section to make the Kuramoto model have discontinuous synchronization.[49]Although, further research showed that bimodal and two Lorentzian frequency distributions also lead to ES in the presence of noise.[50,51]

Fig.1.Order parameter.The magnitude and phase of the resultant vector show the order parameter,r, and mean phase, φ.In this figure, panel (a)shows a relatively coherent and panel(b)shows an incoherent state.

The previous studies analyze the Kuramoto model in the fully connected networks, but complex networks with different connectivity structures are explored in recent researches.Considering the Kuramoto model in these structures requires defining the connectivity matrixAi,j=[ai,j]which represents whether nodeiandjare coupled (ai,j=1) or not (ai,j=0).So,equation(1)becomes

where λi,jdenotes the coupling strength between nodeiandjand regularly equals a fixed value λ.

In Ref.[52], researchers found that by slight changes in the construction of the random network, the Achlioptas process(not ER method),the percolation transition changes from first order to second order.In addition, this explosive percolation was observed in the SF networks with an appropriate value of γ in their degree distribution function,P(k)∝k−γ.[53]Such explosive behaviors in these complex networks encourage the researchers to explore the synchronization transitions in these situations.

2.2.Correlated frequency-degree(CFD)framework

The existence of explosive percolation in SF networks encourages the researchers to inject the heterogeneous to the dynamics of the oscillators.For the first time,Gmez–Gardeeset al.proposed a framework in which the frequency of the Kuramoto oscillators is positively correlated to their degree.Hence, in the simplest form ωi=ki.They considered an algorithm[54]that generated the networks that vary from scalefree(BA)to random(ER)ones using the control parameter α.Consequently,equation(3)changes to

Figures 2(a)and 2(b)show the order parameter as a function of the coupling strength for ER and BA structures,respectively.The ER(Fig.2(a))has the second-order while the BA structure(Fig.2(b))has the first-order transition.It should be noted that the authors also studied other SF networks(different values of γ),and they derived that for different SF structures,the model shows ES while the positive correlation between the degree and intrinsic frequency is established.

To better understand the nodes’clusters in this model,the effective frequency is averaged over the nodes have the same degree,as given by

where the effective frequency,ωeff

i,is given by

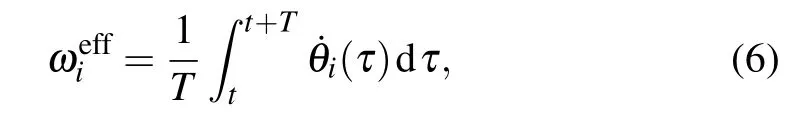
forT≫1.In the second-order transitions (Fig.2(c)), clusters gradually join the final synchrony state,in contrast to the first order(Fig.2(d)),in which clusters are unified abruptly at λc=1.4.

This article also considered the star structure, a mathematically analyzable configuration, to further investigate the ES phenomena in SF networks.This configuration has a hub andKleaves all connected to the hub.As the correlation between the frequency and degree is considered in this framework, intrinsic frequencies of the hub and leaves are equal toKωiand ωi,respectively.Therefore,the phase velocity of the nodes are

where subscriptshandldenote hub and leaf, respectively.=K−1/K+1 and=K/K+1 have been derived analytically in this star configuration.It should be noted that if ωi=kiω,we have,then=[(K−1)/(K+1)]ω.[55]

Calculating the critical coupling strength in the forward transition is somehow problematic in the frequencydegree correlation, but some researchers tried to analyze it numerically.[55–57]

In another work, the authors in Ref.[58] investigated whether the negative correlation between the frequency and degree yields abrupt transition or not.They found that the synchronization transition changes from ES to a hierarchical one as the correlation varies from positive to negative value.

Assortativity,the tendency of the nodes to connect to the nodes which have the same properties,e.g., the same degree(degree–degree correlation), was also explored in this framework using the mixing coefficient,η.[59]

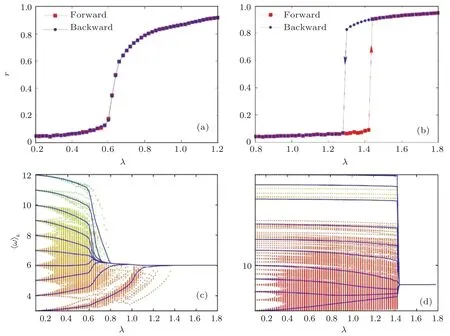
Fig.2.Panels(a)and(b)show forward and backward continuations of the order parameter in the CFD framework.Panels(c)and(d)represent changes in the effective frequencies of the nodes(dotted)that have the same degree(solid blue curves)in the FW continuation.For both structures,δλ =0.2,N=103,and〈k〉=6,reprinted from Ref[41].

Figure 3 (Ref.[58]) shows that the first-order (Fig.3(a)) changes to the second-order (Fig.3(b)) transition as the mixing coefficient changes from negative(disassortativity)to positive(assortativity)value.In this BA structure,N=1000,δε =0.001,and γ =3 inP(k)=k−γ.In conclusion,reference[60]performed a comprehensive study about the degree-degree correlation in SF networks.They showed that a moderate mixing coefficient significantly increases the width of the hysteresis loop.

Fig.3.Effects of changing the mixing coefficient,η,in SF structure under CFD framework.Panels(a)and(b)show the evolution of the average frequencies for the nodes with the same degree.In panel(a), η <0(degree disassortativity)makes the model show ES,but in panel (b), η >0(degree assortativity)causes the second-order transition(Reprinted from Ref.[58]).

Another issue that has mattered in CFD frameworks is noise in structures that did not have ES before.[61,62]For example, reference [61] analytically and numerically showed that considering uniformly distributed randomness in the frequency and degree relationship, in a way that ωi=ki+ξi,make even the mildly heterogeneous networks show ES.

2.3.Frequency gap conditioned(FGC)framework

In the CFD framework, the frequency distribution is determined with the degree probability function,g(ω)=P(k),which restricts exploring the effect of changingg(ω).Contrary to the previous framework that the network structure is defined arbitrarily,another framework is proposed in Ref.[63],where the adjacency matrix is constructed from the frequency difference of the nodes.In this way, nodesiandjare neighbors if they satisfy the following condition:

where γ is a positive constant.In Ref.[63], the authors consided different frequency distributions whileN=500 nodes in all of them.Figure 4 shows the average of the order parameter,S=〈r(t)〉T,as a function of the coupling strength for uniformly distributed frequency in ω ∈[0,1].In addition to the frequency gap (Fig.4(a)), γ, the authors also considered the effect of average connection (Fig.4(b)), 〈k〉, in ES.Results show that for γ =0,the transition is continuous,and for a sufficiently large value of γ, the transition is abrupt, and a hysteresis loop appears.Also,different values of〈k〉shift the hysteresis along thedaxis.

Interestingly,a nonlinear V-shape correlation between the frequency and the degree appears (upper panel of Fig.4(d)),which does not exist when γ =0 (upper panel of Fig.4(c)).Considering the average value of the neighbors’ frequency〈ωi〉 for each node (lower panel of Fig.4(d)), the highfrequency oscillators are connected to the low-frequency ones.It should be noted that the analytical results of this article,shown with a solid red line, claim this correlation.This nonlinear relationship also exists when asymmetrical Rayleigh[64]distribution is used forg(ω).The resulting network constructed from the FGC framework has an ER-like structure.[63]

Fig.4.Panels(a)and(b)Change in order parameter,S,for the FGC framework in different values of gap(γ)and mean degree(〈k〉).Panel(a)shows that for sufficiently large γ,ES with considerable hysteresis length appears in FW(solid)and BW(dashed)continuations when〈k〉=40.In panel(b),it is clear that increasing〈k〉moves the hysteresis loop through the d direction for γ =0.4.Panels(c)and(d)show the relation between the nodes’degree and mean frequency with corresponding intrinsic frequency when γ =0 and γ =0.4,respectively(Reprinted from Ref.[63]).

Another condition is considered in this framework in which the frequency of the node should have a predefined difference with its neighboring nodes.[63]This condition is given by the following expression:

where 〈ωj〉 is the average value over the neighbors.Figure 5(a) shows the first and second-order transitions for uniformly distributedg(ω) for γ =0.4 and γ =0, respectively.The V-shape correlation ofkiand ωiremains in this condition,too(Fig.5(b)).Moreover,figure 5(c)shows that ES and V-shape relationships occur for the Gaussian frequency distribution(the inner panel).

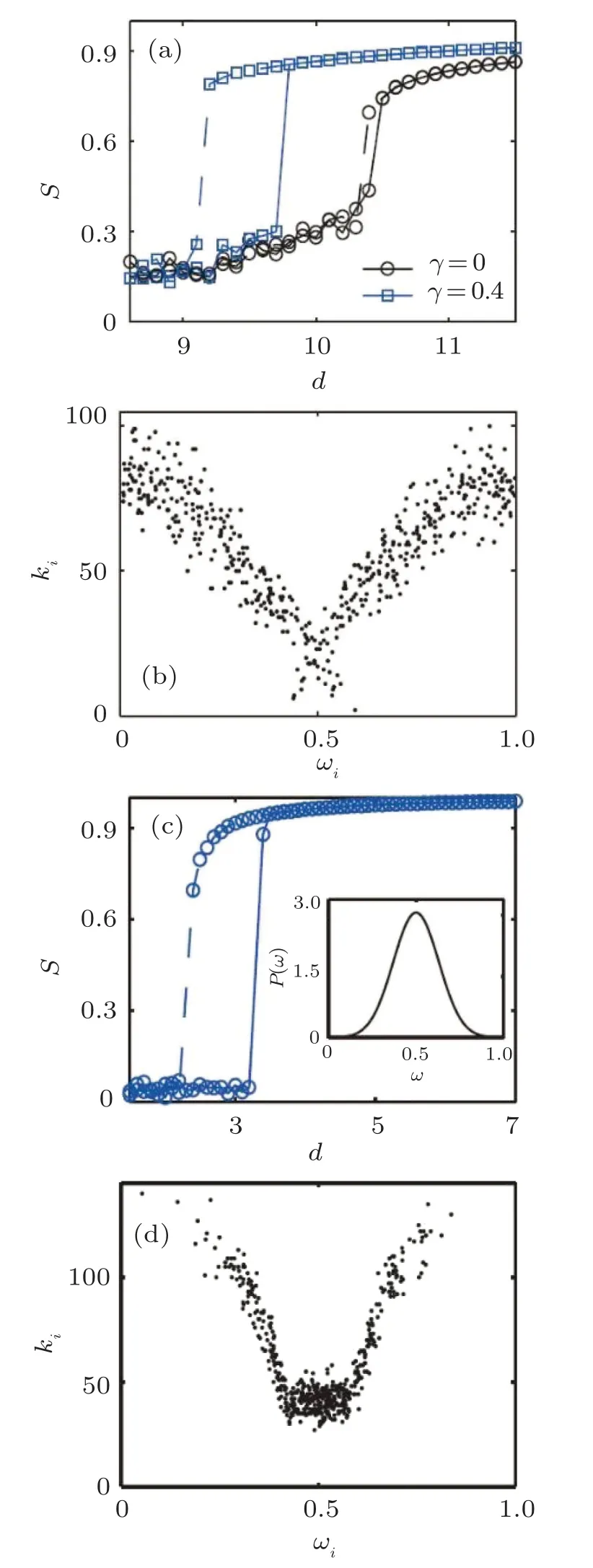
Fig.5.Different frequency distribution effects in the second condition of the FGC framework.Solid and dashed lines respectively show the FW and BW continuations of order parameters for(a)uniform and(c)Gaussian distributions.The V-shape relation between the ki and ωi exists in(b)uniform and(d)Gaussian distributions.Reprinted from Ref.[63].

2.4.Correlated frequency-coupling(CFC)framework

Previous frameworks show how the correlation between the dynamical properties of the oscillators and the structural features increase the possibility of ES in different models.In 2013, the authors in Refs.[65–67] proposed new weighting functions which increase the hysteresis length in different frequency distributions and network structures.In Ref [65],NKuramoto oscillators are coupled according to the equation

Uniform, Gaussian, bimodal, Rayleigh, and semi-Gaussian frequency distributions are considered(Fig.6(a))in the homogeneous random network (ER), while all these distributions are within[0,1]andN=500.[65]Moreover,results show that for linear weighting function(α =1),all these distributions show ES with the same hysteresis loop.

The parameterSi=is defined, which shows the strength of nodei-th.Like the previous framework,the intrinsic frequencies have a spontaneous, not predefined, relationship with the strength of the corresponding nodes.This relationship is shown numerically and analytically for the uniform distribution when α =1(light blue circles and the solid curve in Fig.6(b)).The uncorrelated relationship is also seen when α =0 for the same uniform distribution with blue squares in Fig.6(b).

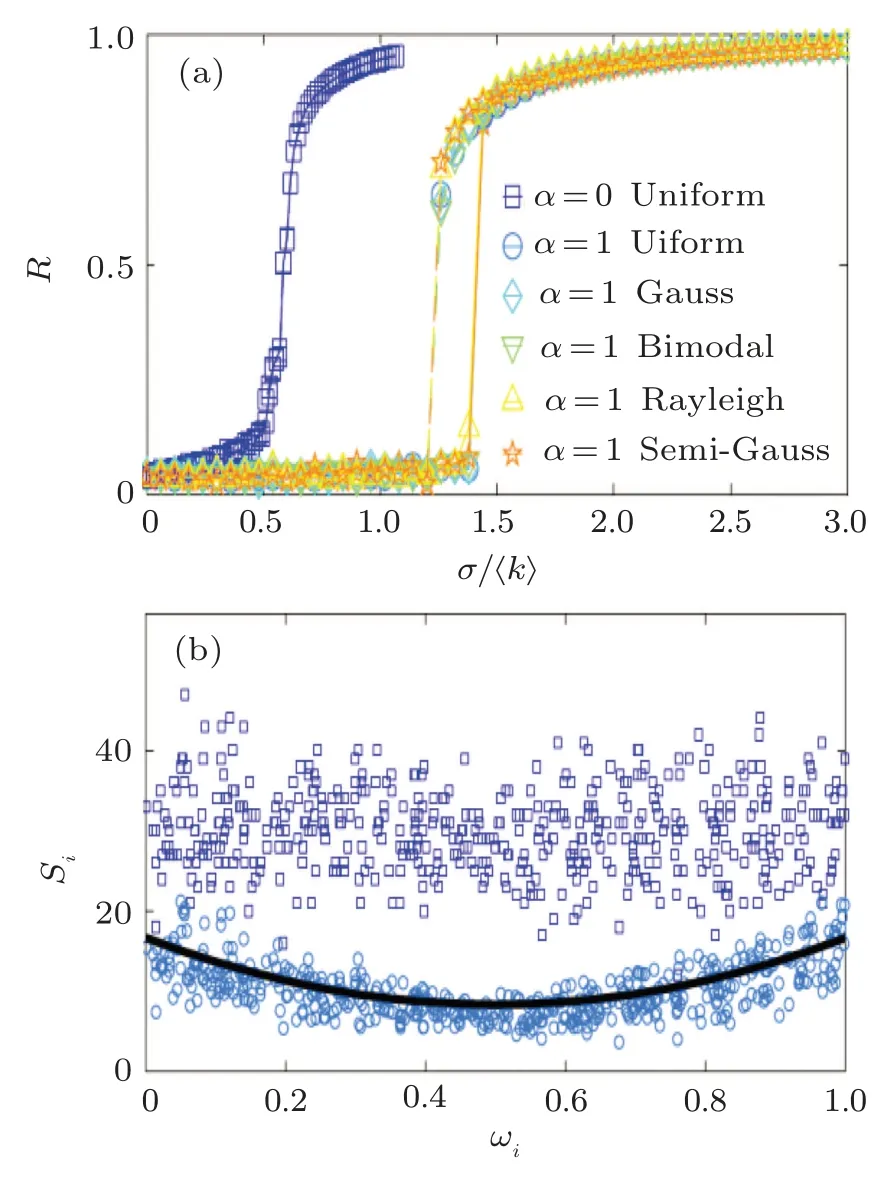
Fig.6.Numerical analysis of CFC framework.(a)The evolutions of R for different frequency distributions show that the appearance of ES in the CFC framework is independent mainly from g(ω).(b)The relationship between the degree of the nodes and intrinsic frequencies is numerically (blue circles) and analytically (black curve) shown in this framework when α =1.The blue squares show the state in which α =0.Reprinted from Ref.[65].

Different scenarios in SF networks (changing the network size, frequency distribution, and super-linearity) show that other weighting functions are needed in these heterogeneous structures to exhibit ES.[65]

Zhanget al.considered the absolute value of the intrinsic frequency as the coupling strength in Ref.[68],which simplifies Eq.(11)to

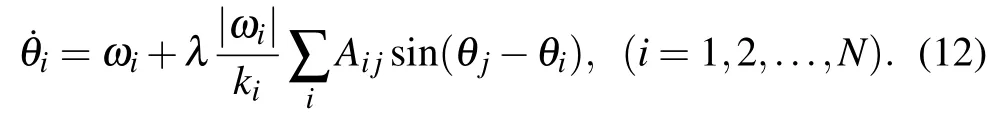
This framework is considered for both Gaussian (µ =0 and σ2=1) and Lorentzian (ω0=0 and γ =0.5) intrinsic frequency distributions in fully connected,ER,and SF structures with 〈k〉=6.As depicted in the following Fig.7, all these cases show ES.

Fig.7.The CFC framework.FW and BW continuations of the order parameter show ES in different topologies and frequency distributions for the CFC framework.(a)Fully connected structure and Lorentzian distribution(ω0 =0 and γ =0.5),(b)fully connected structure and Gaussian distribution(µ =0 and σ2 =1),(c)ER structure and Lorentzian distribution,and(d)UCM structure and Lorentzian distribution.For all four panels〈k〉=6.Reprinted from Ref.[68].

2.5.Adaptive framework

The coupling between the oscillators can be effectively tuned using the activity of the oscillators, as demonstrated in Refs.[69–71].Considering this, the authors in Ref.[72] proposed a modification of the Kuramoto network, which is both analytically and numerically discussable.In this model,the coupling between the oscillators is dependent on the activity of all oscillators,so is the global order parameter.Equation(3)is then modified to

wherezis the control parameter.The model shows ES with a hysteresis loop forz>1.

Fig.8.FW continuation(filled circles),BW continuation(open circles),and analytical results(solid curves)of the order parameter for Eq.(13).In panels(a)z=0.7,(b)z=1.5,(c)z=2,and(d)z=3.Reprinted from Ref.[72].

Figure 8 shows the continuous and abrupt(with and without hysteresis)in this system when(a)z=0.7,(b)z=1.5,(c)z=2,and(d)z=3.

Considering the previous work, in 2015, Zhanget al.[73]proposed a new framework that includes the interaction between the coupling strength and the local order parameter in a fraction of nodes.This framework is formulated as the following expression:

in which for a fraction of the nodesf,αiis calculated as follows:

and for the otherN(1−f)nodes,αi=1.

This article shows anfcfor which iff>fc,synchronization is explosive (Fig.9).In addition,fis also a control parameter that can change the hysteresis loop length, 〈d〉.This could be observed in the upper panel within Fig.9, showing the hysteresis loop length〈d〉and the lower panel showing the forward and backward critical coupling strengths.Forf>fc,the hysteresis width grows in this ER and homogeneous frequency distributed model withN=100,〈k〉=12.They considered this framework in the two-layer network, which will be discussed later.

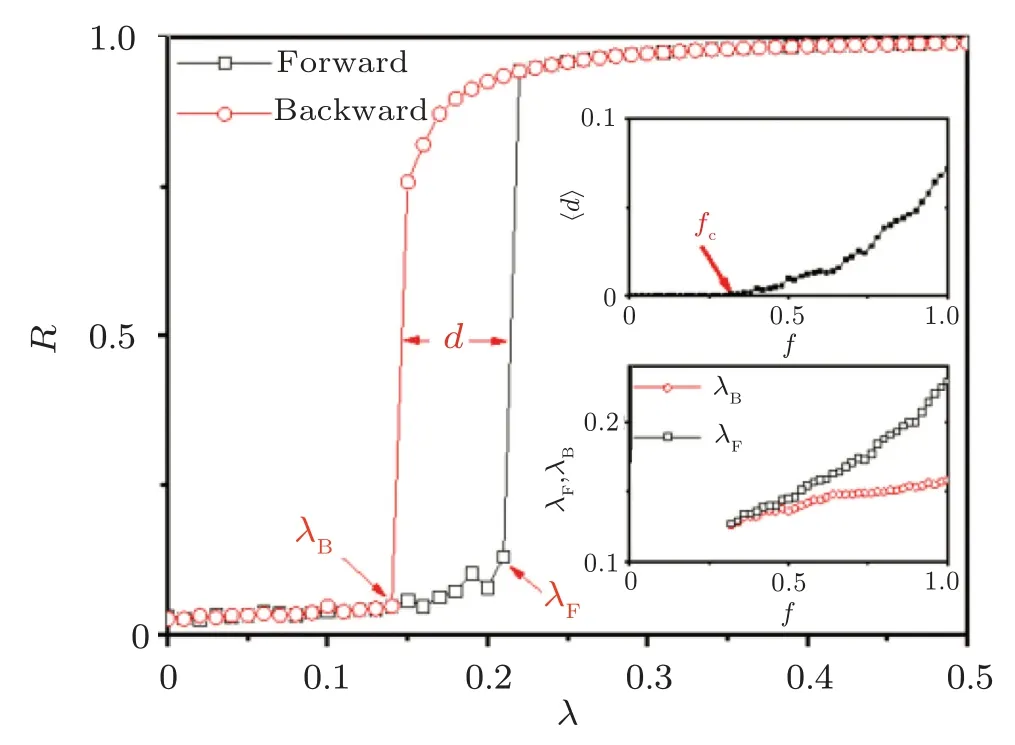
Fig.9.The synchronization transition of the adaptive framework as a function of coupling strength(black square: FW and red circle: BW).The inner panels show the average hysteresis length, 〈d〉, γF and γB as f increases.Reprinted from Ref.[73].

In another adaptive framework, the relation between the oscillators is divided into a cooperative(αi=R)and competitive (αi=1 −R) mechanisms.[74]This model is inspired by the neuronal system in which both inhibitory and excitatory neurons exist.Some disorders like epilepsy and fibromyalgia,characterized by ES, result from the imbalance between the activities of these two neuron types.There are ρNcooperative and(1−ρ)Ncompetitive oscillators in the model described in Ref.[74].The forward and backward evolution of order parameters (Fig.10(a)) for ρ =0.2 and ρ =0.8 show that the transition is the first and second orders, respectively, in ER network.Also,figure 10(b)shows the evolution of this model in the BA network for ρ=0 and ρ=0.8.The inner left panels show that the hysteresis length,〈d〉,decreases as ρ increases.The disappearance of ES is also evident from the inner right panels,which show the alterations of〈λF〉and〈λB〉.

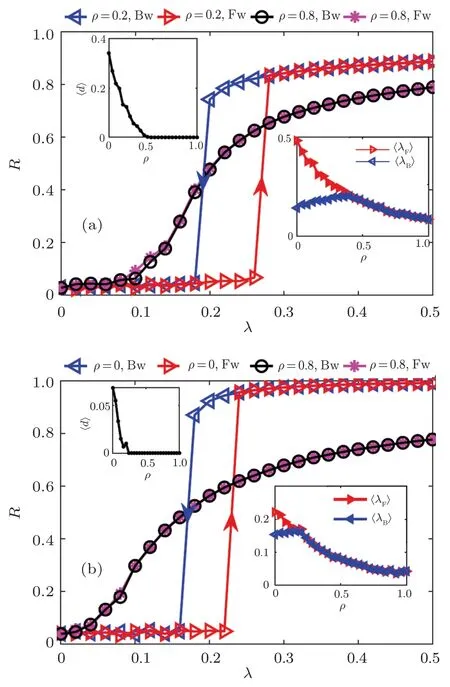
Fig.10.The effect of fraction of cooperative(f)oscillators on order parameter,R,and the average hysteresis width,〈d〉,in ER(a)and BA(b)structures when N=1000 and〈k〉=12.Reprinted from Ref.[74].

In an exciting work, the oscillators can move in a twodimensional (2D) plane.[75]Each dynamic oscillator is coupled to oscillators placed in its vicinity(a circle with radiusR).Numerical analyses of this article show that for large enoughR, the transition to synchronization is abrupt (Fig.11(a)).Also,for smallRvalues,increasing the velocity of the oscillator(the length it passes in one iteration),v, helps to compensate for the existence of ES(Fig.11(b)).

In real-world systems, like biological and social networks,considering all the nodes and links in just one level is a significant constraint.[76–78]Therefore,different levels(layers)of connection should be considered in complex systems.Several types of research consider multilayer networks’results details and accurate descriptions of the practical problems[79–82]The term synchronization in multilayer networks is more complicated than the monolayer one.Reference [76] provides a good guideline on this issue.

Fig.11.Order parameter(r)in moving oscillators.In panel(a),as the radius(R)of the oscillators’vision increases,the synchronization transition becomes abrupt when N =500 and the velocity, v=0.02.In panel (b), while the radius is small (R=0.1), increasing the velocity makes the system show ES.Reprinted from Ref.[75].

Some investigators[62]who proposed the adaptive framework,also considered this context in the multilayer network.In this way,two independent layers with the same size(N)and same fraction of nodes(f)are coupled using the following equations:

where subscripts 1 and 2 represent the first and second layers, respectively.αi,1and αi,2are the couplings between these two layers and for fractionfof the nodes equal tori,2andri,1respectively.Note that the coupling strength in one node depends on the order parameter,so the local synchronization level of the corresponding node in the other layer.

The evolution of the two-layer network order parameters is shown in Fig.12.The first layer has a random homogenous frequency distribution in the [−1,1] interval with an ER network in which〈k〉=12 and the second layer is the same as the first layer with independent intrinsic frequencies’distribution in panel (a).The evolution of the average hysteresis length(〈d〉) is shown in the inner panels.Forf>fc, this average increases from zero to positive values.In Fig.12(b), the second layer is the same as the case (a) but 〈k〉=6.The inner panel of Fig.12(b)shows that〈d〉>0 for greaterfccompared to Fig.12(a).In Fig.12(c), the second layer is the same as panel(a)but the frequency distribution is Lorentzian(ω0=0 and γ =0.5).The BA structure with〈k〉=12 is also considered for the second layer in Fig.12(d).Results showed that this two-layer framework can exhibit ES transition for different second layer structures.

Fig.12.The ES transition in a two-layer network for different single-layer properties.The inner panels show the average hysteresis length for these four different states.The first layer has a random homogenous frequency distribution in the[−1,1]interval with an ER network in which〈k〉=12 and(a)the second layer: like the first layer but the intrinsic frequencies’ distribution is independent of the first layer, (b) the second layer: same as the panel (a) but〈k〉=6,(c)the second layer: the same as panel(a)but the frequency distribution is Lorentzian(ω0=0 and γ =0.5),(d)the second layer: like the panel(a)but the network is BA with〈k〉=12.Reprinted from Ref[73].

2.6.Simplicial complexes and higher-order couplings

Networks can be analyzed by investigating the existence ofk+1 fully connected nodes,i.e.,ak-simplex.[83–85]Recent studies show that besides pairwise coupling, higher-order interactions, particularly simplicial complexes, significantly influence the collective behavior of complex networks.[83,86,87]Also,considering the 4-simplexes of Kuramoto–Sakaguchi[88]systems can yield chaotic behavior.[89]Moreover,higher-order Kuramoto networks are analyzed in abrupt synchronization transition.[90–92]In this framework, equation (3) is modified to 3-simplexes of Kuramoto oscillators given by

whereK1,K2, andK3are 1-, 2-, and 3-simplex coupling strengths.Also,Ai j,Bi jl, andCi jlare 1-, 2-, and 3-simplex adjacency tensors.Therefore, averaging the number ofqsimplexes each node is a part of,, indicates the parameter〈kq〉 in the above equation.In Ref.[91], two different realworld networks are considered,Macaque brain and UK power grid networks.In these two networks,adjacency matrixAand adjacency tensorsBandCare derived from the undirected links, triangle, and tetrahedron structures.For the brain network,the parameters are set asK2=1.6 andK3=1.1.In this case, increasing (and decreasing) the 1-simplex coupling results in abrupt transition in the order parameter,r(Fig.13(a).Thus,the red point in the FW continuation is shown on the unit circle (Fig.13(b)), an incoherent state withr～0.07.On the other hand, the blue point in BW continuation is a relatively coherent state withr～0.46.

Interestingly, the UK power grid network shows abrupt synchronization for negative values (repulsive interaction) of the 1-simplex coupling strength.In this case,K2=2.2 andK3=3.3.

Fig.13.ES in Macaque Brain Network(a)and UK Powergrid(d)in which oscillators are coupled with simplicial complexes. K1 is the 1-simplex coupling strength.Panels(b)and(c)show the distributions of the oscillators on the unit circle for the FW (red) and BW (blue) continuations, respectively.In panel(a)K2=1.6 and K3=1.1 and for panel(d)K2=2.2 and K3=3.3.Reprinted from Ref.[91].

Fig.14.The 2D bifurcation diagram of an all-to-all connected network as a function of K1 and K2+K3.The collision of the pitchfork and saddle-node bifurcations divide the region into three different states;incoherent,bistable,and synchronized conditions.Reprinted from Ref.[91].

In contrast to previous frameworks,this study shows that ES may appear in systems with no predefined correlation between the oscillators’structural properties and dynamical features.They also investigate 1-, 2-, and 3-simplexes in an all-to-all connected network withN=10000.Hence, in this mathematically solvable problem,a two-dimensional bifurcation diagram of the order parameter is considered whenK1andK2+K3are the control parameters.The collision of the pitchfork and saddle-node bifurcations divide the region into three different states; incoherent, bistable, and synchronized conditions as shown in Fig.14.

Table 1 shows different frequency distributions and degree distributions that have been used in these frameworks.In the CFD framework, the degree of each node restricts its frequency.So, different frequency distributions could not be explored in this framework.Also, in the FGC framework,the algorithm makes the degree distribution ER-like.In CFC,adaptive, and simplicial complexes frameworks, ES’s existence does not mainly depend on the frequency and degree distributions.So, these frameworks seem to be more appropriate for further investigations.It should be noted that in the simplicial complexes framework, contrasting to others, there is not any predefined relationship between the network structure and the oscillators’dynamical features.

Table 1.Frequency distribution and network structures in each framework.

3.Explosive synchronization in the language of mathematics

The main question is, why does the ES happen? Is it a universal route or interplay between the network’s structure and the oscillator’s dynamics? Although the previous studies discuss the ES due to the interplay between the network structure and the oscillator’s dynamics, there is no apparent correlation among them in the simplicial complexes and the higher-order couplings.[91,92]]

Fig.15.Bifurcation of the criticality in the (x>0,p,q) space.Dashed and solid lines indicate the instability and stability of the equilibrium, respectively.This figure shows how the subcritical(gray), first-order, can be changed to the supercritical (black), second-order, with primary parameter p and additional parameter q.Panels (a) and (b) show these criticality changes in transcritical and pitchfork bifurcations, respectively.Reprinted from Ref.[93].

In Ref.[93],the authors mathematically argue that ES is a universal/generic phenomenon in nonlinear systems in which other features are added to the classical model.They also generalize this universality to critical epidemic behavior and explosive percolation.Remarkably, this article discusses the potential of an additional parameter to change the criticality of a transcritical or pitchfork bifurcation,i.e., a supercritical(in both transcritical and pitchfork) bifurcation, second-order transition, changes to subcritical, first-order transition, in a model with two parameters,[94]as illustrated in Fig.15.

4.Explosive synchronization in different dynamical oscillators

4.1.Phase oscillators

The Kuramoto model is discussed in the majority of the articles, which focus on ES.Some of the pioneer and essential articles are discussed in this review.This section analyzes other modified versions of this oscillator,e.g., Sakaguchi–Kuramoto and second-order Kuramoto models.

Sakaguchi–Kuramoto(SK)generalized the standard Kuramoto model with the phase frustration term, which seems crucial from the empirical perspective.[88]So, equation(1)changes to

where α is the phase frustration term ranging[0,π/2).

The SK model is considered in different frameworks and network structures.A star graph, the simplest form of the SF network of SK oscillators, is mathematically analyzed in the CDF framework.[95,96]Numerical results show that phase frustration can induce ES and control the hysteresis loop length in SF networks.[95–97]Moreover, the partial CDF framework,correlation between degree and frequency in fractionfof higher degree nodes, is analyzed numerically and mathematically.[98]Results show that both the parameters,fand α,change the transitions to synchrony.

Unlike the previous frameworks, reference [99] showed that the frustration term of SK oscillators in the FGC framework destroys the ES and attenuates the synchronization.In this study, the frequency of each oscillator is given by ωi=(i−1)/(N−1); alsoN=400, γ =0.6, and the number of edges (L) is equal to 4000.Figure 16 shows that explosive and even synchronization disappear as the frustration term(α)increases.

Fig.16.Sakaguchi–Kuramoto oscillators in the FGC framework.The FW and BW synchronization evolutions show that increasing α from(a)0.25π to(b)0.5π change the transition from first-order to second-order.Reprinted from Ref.[99].

Using an adaptive function for the coupling of the SK oscillators[100]changes Eq.(19)to

whereZ≥1 is the control parameter.Interestingly, the existence of ES and improving the hysteresis width in this framework is independent of the network structure and frequency distribution.

Figure 17 shows the incoherent(I),hysteresis(II),and coherent(III)regions of the SK model as a function of parameterZand the coupling strength in the SF(γ =2.8)network.It is shown that as the parameterZincreases,the area of the region I increases,so the length of the hysteresis loop enhances.The frustration term equals (a) zero and (b) 0.5 in this figure.In both panels the SF network hasN=2000 nodes with average degree 〈k〉=12.Also, the intrinsic frequencies are chosen from a Lorentzian distribution with ω0=0 and σ =1.

Fig.17.Amplification of the ES in the Sakaguchi–Kuramoto model with an adaptive framework.Regions I,II,and III show incoherent,hysteresis,and synchronized states,respectively.It is shown that as the z increases,the region I increase increases,so the length of the hysteresis loop enhances.The frustration term equals (a) zero and (b) 0.5 in this figure.Reprinted from Ref.[100].

Also, this model is used in CFC,[101]multilayer,[102,103]and adaptive connection matrix[104]frameworks which make the role of the frustration term more evident in the ES generation.

The second-order Kuramoto, a modified version of the Kuramoto model including inertia,[105]is analyzed numerically and mathematically in Ref.[106].In this model,

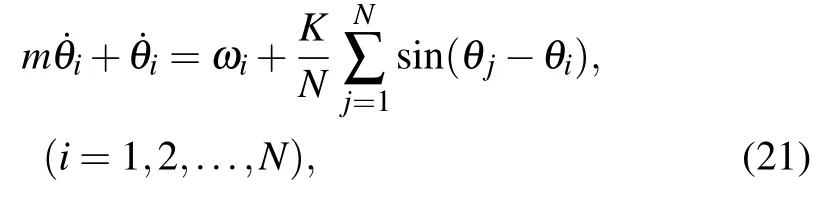
wheremis the inertia and frequencies ωiare uniformly distributed in [−ΩM,ΩM].In this article, the authors confirmed that numerical results ofN=500 second-order Kuramoto oscillators are consistent with the theoreticalandwhenm=0.85 and ΩM=5.

4.2.Chaotic systems

Extending the notation of order parameters to chaotic oscillators needs defining phase for these systems.Pikovsky et al.proposed different definitions of phase in chaotic oscillators.[23]Crossing from a predefined surface, the Poincare section,is considered as 2π increase of the phase in the first definition:

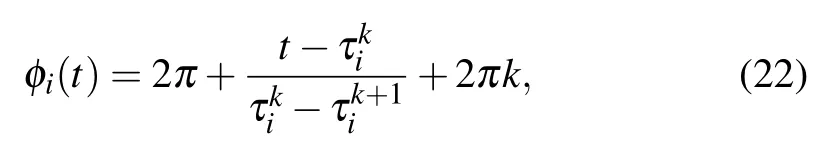
In the second definition, the angle between the two state variables is considered as the phase of the chaotic oscillator,[110]

It should be noted that the mean frequency defined based on both phase definitions is equal despite inequality at the microscopic level.

The parameterris averaged amongNoscillators.Another synchronization parameter is proposed for a small number of oscillators,which calculates this average amongN(N−1)agents:[109,111]

whereS∈[0.5,1]with minimum and maximum values of this interval showing incoherent and complete synchronized states,respectively.Therefore,one can calculate the order parameter for the chaotic oscillators using Eq.(2) or Eq.(24) with the phase of the nodes.

In the following sections, different chaotic attractors in the context of the abrupt transition are discussed.

4.2.1.Rossler system

The Rossler system is the first chaotic system considered in the CDF framework.[110]The network ofN=1000 coupled piecewise Rossler is considered in the SF structure as

whereg(xi)andvfunctions are given by

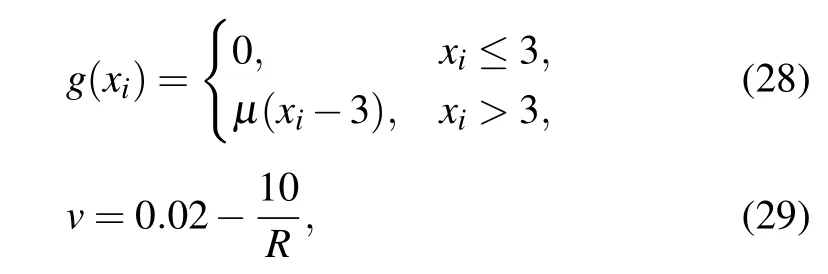
wherex,y, andzare the system’s state variables; β, ε, Γ,andRare constant system parameters;dandAi,jare coupling strength and adjacency matrix,respectively.Parameter αiprovides the CDF framework for the Rossler network,as it correlates the frequency of the oscillators with their degree of connections(ki)as

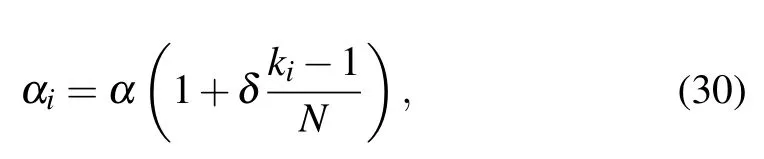
where α and δ are constant parameters of the above definition.In this study, the phase of the oscillators is calculated using Eq.(22), and the order parameterS(Eq.(2))is used to quantify the synchronization.

Fig.18.Piecewise chaotic Rossler oscillators in the CFD framework.FW(solid)and BW(dashed)continuations of the order parameter,S,as the coupling strength changes when γ =2.2(red),γ =2.5(green),and γ =3(blue and black).The system shows an abrupt transition to synchrony for red,green,and blue states,in which δ =10.0 and R=100.However,in the case of δ =6.0 and R=70, the black curve, the system shows the continuous transition.Reprinted from Ref[110].

Figure 18 displays the order parameters of systems(25)–(28)as a function of the coupling strength in the CFD framework.The FW (solid curve) and BW (dashed curve) continuations are shown in the figure when γ =2.2 (red curve),γ =2.5 (green curve), and γ =3 (blue and black curves).In all these SF networks,N=1000 and〈k〉=12.Thus,the system shows an abrupt transition to synchrony for red, green,and blue states,as in which δ =10.0 andR=100.However,in the case of δ =6.0 andR=70,the black curve,the system shows the continuous transition.

4.2.2.Lorenz system

Most studies show that the interplay between the dynamical features of the system and the structure provides the circumstances for systems to show ES.Meanwhile, the authors in Ref.[112]considered the Lorenz system in the SW and SF networks.Interestingly, synchronization ofN=200 coupled Lorentz systems with 577 edges occurs abruptly in SW and SF structures.This is because all the state variables of one node are coupled to corresponding ones regarding the adjacency matrix.

The order parameter in this chaotic network is defined as

wherer= 0.03 is the error between the two synchronized signals which is acceptable and θ is the Heaviside function.When all Lorenz oscillators are synchronized,p(t)=1 while in the incoherent statep(t)=0.Figure 19 shows the ES in the described system for both SF and SW systems.

Fig.19.The ES transition in Lorenz networks.This figure shows the evolution of the order parameter, p, for some different initial conditions in panel(a)SW and panel(b)SF networks.Reprinted from Ref.[112].

4.3.Neuronal models

The existence of abrupt transitions in biological phenomena encourages examining different neuronal models in different frameworks of ES.In the following sections, the articles that consider different neuronal models are reviewed from ES point of view.

4.3.1.Hodgkin-Huxley (HH) neuronal networks

In 1952, Hodgkin and Huxley proposed a fourdimensional (4D) differential equation that formulates the voltage of the intracellular membrane.However, the parameters were estimated through voltage clamp and space clamp of the giant squid axon;this model is widely used to describe the different physiological and pathophysiological situations in humans.Also, the collective behavior of coupled HH neurons has been discussed in various studies.Synchronization transition in a complex network of connected HH oscillators is discussed under chemical and electrical synapses.[111]In these cases, SF, SW, and random networks are considered to study the heterogeneity of network structure.The SW network shows ES in electrical coupling between these structures (Fig.20).The Watts–Strogatz network withN=500 nodes with mean degreez=50 is considered for both panels.However, the article also considered the networks while the frequency of the neurons is correlated with their degree (z).The result shows that SF networks can exhibit ES in the CDF framework and electrical coupling(Fig.21).

Fig.20.The FW and BW synchronization in Hodgkin–Huxley neural network with (a) electrical and (b) chemical couplings.Reprinted from Ref.[111].

Fig.21.The HH network in SF structure with the frequency-degree in correlated and uncorrelated cases.In panels(a)and(c),the coupling is electrical while in In panels (b) and (d) chemical coupling is used as the interaction between the oscillators.Reprinted from Ref.[111].

In all these numerical results, the phase of each neuron and the order parameter are calculated using Eqs.(22) and(24),respectively.

4.3.2.Izhikevich neuronal networks

In 2003, Izhikevich proposed a biologically meaningful model which is also computationally efficient and time-saving.This two-dimensional(2D)differential equation can generate both spiking and bursting mode of the neuron,varying four parameters of the system.[113]Khoshkhouet al.considered the Izhikevich model in the ring, SW, SF, and random networks with electrical and chemical couplings.[109]Meanwhile, ER(Fig.22(a)) and SF (Fig.22(b)) structures exhibit ES with a significant hysteresis loop in electrical coupling conditions.

Like the HH model,the phase of each neuron and the order parameter are calculated using Eqs.(22)and(24),respectively.In both these structures,N=1000 andz=50.

Fig.22.The FW and BW synchronization transitions.The evolution of the order parameter shows that in both ER(a)and SF(b)structures,the network shows ES when the coupling is electrical.Reprinted from Ref.[109].

4.3.3.FitzHugh-Nagumo (FHN) model

FitzHugh–Nagumo model is another 2D model which is biologically meaningful and has been used to model different brain conditions.Noise-induced,non-identical,coupled FHN oscillators are considered in both SF and ER random networks under the CDF framework.[108]As this model was studied in previous reviews,[42,43]it should be noted that the ES’s existence in this model depends on the slope of the frequencydegree correlation function,δ (Fig.23).

Fig.23.The hysteresis length of the FitzHugh–Nagumo oscillators in the BA structure.In this network,N=200,ε =0.01,Dx=0,Dy=0.005,and〈k〉=6.Reprinted from Ref.[108].

4.3.4.Map-based Chialvo neuronal model

Although the neuronal ordinary differential models are developed well, their simulation is time-consuming.[114]Moreover, they also have parameters that generalize these models hard for new condition studies.[114,115]To overcome these limitations,map-based models have been used,discretizing the ODE models or analyzing the fast and slow behavioral dynamics of a neuron,[116,117](e.g., map-based Izhikevich model,[113]Rulkov model,[118]and Chialvo model[119]).

Chialvo model is a 2D map-based model that can generate some excitable neuron generic behaviors.[119]The network of Chialvo oscillators can be presented by[120]

wherexi,tandyi,tare the fast and slow variables,respectively;kiis an additive noise selected randomly from the interval[0.03,0.03+σ] for each neuroni;a,b, andcare model parameters;ε is the coupling parameter that normalizes with the average number of connections(η);ei,jare the elements of the adjacency matrix.

UsingN=1000 dissimilar Chialvo neurons,in Newman–Watts SW[121]structure, yields ES with different hysteresis loop.The length of the hysteresis loop is dependent on the value of σ, which changes thekiparameter interval and the nonlocal connection probability of the network(Fig.24).

Fig.24.The temporal average order parameter of Chialvo oscillators in the Newman–Watts structure.For different values of the parameter σ, which determines the maximum in the accepted interval of the additive noise, the system shows ES.Reprinted from Ref.[120].

In this article, the bistability of the non-synchronized chaotic state and a phase-synchronized state is considered as the mechanism behind the existence of ES.As the coupling parameter increases,the basin of attraction of the chaotic nonsynchronized state becomes smaller until it vanishes.Also,the same happens for the phase-synchronized state when the coupling strength decreases from the maximum value to ε =0.

The existence of ES without any defined framework in the Lorentz network shows the potential of chaotic oscillators in this context.Although using chaotic systems in large networks often makes the calculation more difficult and timeconsuming, these models are closer to the reality of the real phenomena.Furthermore,with their extreme sensitivity to initial conditions and intrinsic parameters,these systems can represent neuronal activities to an acceptable extent.Even though the HH model is the most detailed model through neuronal models,considering other models like Izhikevich is more appropriate and reasonable.As seen in this section, Izhikevich networks can show ES in both SF and ER structures.However,map-based models are more applicable for large networks than ordinary differential equation ones.For further analyses,considering the chemical and electrical couplings’effect on mapbased models makes them more realistic.

5.Explosive synchronization in real-world and experiments

Besides theoretical studies, experimental investigations have been done which show practical aspects of ES.In addition,abrupt transitions in some biological phenomena express the existence of this mechanism in response to the changing intrinsic and environmental parameters.

5.1.Real-world explosive synchronization

The cochlea, where sound transduction occurs, is the frequency-sensitive organ in the auditory system.[122]Analyzing the hierarchically coupled hair bundle oscillators helps understand the mechanism of frequency selectivity in the cochlea.[123]The proposed model coupling strength has both imaginary and real parts, representing both phase and amplitude.Results show that considering the model parameters so that the oscillators abruptly synchronize yields better frequency selectivity of the model.

Analyzing the experimentally derived brain networks show the existence of(i)frequency degree correlation,(ii)disassortativity, (iii) frequency mismatch of coupled units, and(iv) difference in global and local properties of the network in the unconscious state.[124]Thus, they prove the hypothesis of the existence of ES conditions in the brain.Moreover, the previous group discussed both explosive and continuous synchronization in unconscious state transitions like coma and sleep.[125]The network structure is constructed like the previous study, but different frequency distribution is assumed for abrupt and continuous transitions regarding the frequency disassortativity in ES.[61,126]Results show that the DTI(Diffusion Tensor Imaging)based networks can generate both these transitions.Additionally, previous studies show the relationship between the structural and dynamical properties of the epileptic brain network using both recording and imaging devices.[127]

Fibromyalgia is a common chronic disease characterized by musculoskeletal, sleep, memory, fatigue, and mood problems.[128,129]Genetic and environmental factors probably,cause a malfunction in central pain processing, which results in hypersensitivity to painful and not painful stimuli.[130,131]Leeet al.hypothesized that hypersensitivity makes the brain have abrupt synchronization in the Fibromyalgia state.[132]In this model,the brain network is constructed using DTI.[133]of 82 Kuramoto oscillators.Evaluation of the networks has led to claims that the system is more sensitive to frequency perturbation in the ES state than the non-ES state.

5.2.Explosive synchronization in experiments

Relaxation oscillators are in the group of nonlinear systems which exhibit non-sinusoidal periodic responses.[134]The charging and discharging of these oscillators can model many physical systems in different fields of interest like engineering,[135]mechanics,[136]chemistry,[137]and biology.[138,139]To investigate the ES phenomenon in relaxation oscillators experimentally, photochemical microoscillators are coupled with the setup shown in Fig.25(a).

Fig.25.The photochemical oscillators in the experiment.Panel(a)shows the experimental setup.Panel (b) displays an example of the camera image.In panel(c),FW and BW continuously show ES in the transition of the photochemical oscillators to synchrony.Reprinted from Ref[140].

These oscillators are coupled using the feedback term,which projected using the camera and projector elements as

wherefi(t)is the intensity of each oscillator.Respectively,KandAi,jare coupling strength and the adjacency matrix chosen arbitrarily.The phase of each oscillator is calculated usingfi(t).Also, the uniform light is projected to calculate natural frequencies at the start of the experiment.

Figure 25(b) shows the output of the camera for an arbitrary connecting matrix.WhileKgradually increases and decreases, the order parameter is calculated using Eq.(2), as shown in Fig.25(c).Abrupt synchronization and a hysteresis loop are discovered in this experiment.

A starlike network of chaotic piecewise Rossler circuit[141]is considered in Ref.[110] to show the generality of the numerical results of this oscillator.

6.Explosive death

Another interesting topic that has not been attended well in the literature of explosive phenomena is explosive death.[142,143]The emergent destruction of oscillations is a collective behavior in coupled oscillators, seen as regular as synchronization.This behavior is divided into two classes;amplitude death (AD)[144]and oscillation death (OD).[145]However,different descriptions exist to characterize these two classes,[146]which denominated inhomogeneous steady-state(coexistence of some steady states) to OD and homogeneous steady-state(HSS)to AD.

A network of N chaotic Lorentz systems is considered in Ref.[147], where these oscillators are coupled with a meanfield diffusion scheme as

where σ =10,r=28, andb=8/3;kis the strength of the coupling and the power of the mean-field,, changes specifically withQ.

Two indices,order parameters,are used to define the amplitude death in numerical results.[147]The first one is termed out from averaging the difference between the output signals’global maximum and minimum values over the nodes.For each coupling strength,

in which〈x···〉tindicates that the maximum and minimum values are averaged over a sufficiently long interval.Thea(k)is then normalized as,

For the death state,A(k)=0 andA(k)are positive for the other states.The second-order parameter is derived from the normalization of the mean incoherent energy,

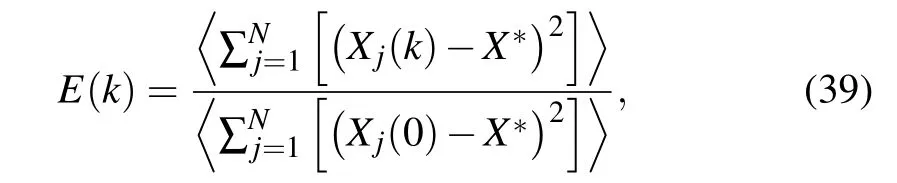
whereXj(0) is the initial conditions andX∗represents the fixed point of the system.Like the previous order parameter,E(k)equals zero when the amplitude death happens in the network.

Fig.26.Explosive death in the network of coupled Lorentz oscillators.Panels (a) and (b) show different order parameters in FW and BW transitions.Panels (d) and (e) show the maximum Lyapunov exponent and the normalized synchronization error, respectively.Comparing these two panels shows that the oscillators have an incoherent chaotic(λ >0)state before the point P.By increasing the coupling strength, this state changes to a coherent chaotic one.(c) OS, HA, and HSS regions are shown in the (Q–k)plane.Reprinted from Ref.[147].

Figures 26(a) and 26(b) showA(k) andE(k) in the FW and BW transitions.Comparing these panels shows that the oscillators’synchronization abruptly changes to an incoherent state and has a hysteresis loop.Panels (d) and (e) show the maximum Lyapunov exponent and normalized synchronization error.Comparing these two panels shows that the oscillators have an incoherent, chaotic (λ >0) state before the P point.By increasing the coupling strength, this state changes to a coherent chaotic one.At the same time,this state does not remain and changes to amplitude death of the oscillators.

7.Conclusion and outlook

Previous studies show the existence of abrupt transitions in the Kuramoto oscillators’network.The intrinsic properties of this oscillator have been considered as the reason for this transition.As reviewed in this article,the previously proposed frameworks can exhibit ES in Kuramoto and other oscillators.These frameworks do not limit the relation between the network’s structure and dynamical properties of the oscillators,which was considered the underlying reason for ES,e.g., the simplicial complexes in which there is no predefined relationship between the coupling coefficients and the structure.Furthermore, one recent study claims that just two generic parameters are needed to change the criticality of the bifurcation from supercritical,second-order transition to subcritical,firstorder transition.So, the presence of other frameworks is not hard to believe.As the Kuramoto model does not have any other dynamical features which can be used in further frameworks,the probable future researches mainly focus on the concept of 2D bifurcation of generic parameters.Also,more analytical studies in previous frameworks help to provide the accuracy of this assumption.

Although the phase oscillators and the Kuramoto model are appropriate models for exploring synchronization, studying other and incredibly chaotic oscillators is necessary.Considering such oscillators is more reasonable in real-world systems, but investing order parameters is more problematic in existing systems.In reality,the first step,i.e.,the definition of phase in these oscillators,is problematic.Also,different order parameters are defined and used in chaotic oscillators, which is considerable with regards to the typical one which always has been used for phase oscillators.Although the Kuramoto model is considered extensively in previously proposed frameworks, chaotic models are not well explored in these structures.Therefore,this is an open challenge to discover.

Considering the neuronal models, like Hodgkin–Huxley,Izhikevich,and Fitzhugh–Nagumo,in the previously proposed frameworks were a great step in modeling the brain network.This researches should be advanced to generalize to other brain states,both physiological and pathological states To consider large networks,future research should focus on the mapbased models of the neuron that are more time-saving and reliable.

Synchronization has both desired and undesired aspects.So,desynchronization,suppression of coherent state is investigated in some applications,e.g., in biological systems, both these aspects can empower the healthy (variety of cognitive functions like attention and memory) and treat disorders and diseases(like epilepsy and Parkinson).As the velocity of the transition increases, its controllability becomes problematic.So, the most challenging situation would be explosive synchronization and desynchronization.Controlling the ES is described as lessening its velocity and turning it into continuous transitions.Few studies concentrate on this topic, and most of them considered their trial and error efforts as the control scheme.In other words, tuning the parameters is not convenient, and other analytical approaches are needed in this issue.Moreover, some of these parameters are generic which the controller may not have access to modify them.