木梁夯土界面粘结滑移性能及其计算方法
陈明杰,罗漪,b,郑双杰,b,杨志林,丁楠
(华侨大学 a.土木工程学院;b.福建省智慧基础设施与监测重点实验室,福建 厦门 361021)



图1 木梁夯土节点Fig.1 Rammed earth-timber


1 粘结滑移试验
1.1 试件设计及制作


表1 试件参数表Table 1 Parameters of specimens
土楼木梁实际间隔为300 mm,夯土墙的厚度为1 000 mm左右,选定夯土试件的尺寸为长×宽×高=1 000 mm×300 mm×300 mm,木梁直径为100 mm,具体尺寸见图2。

图2 木梁夯土节点试件尺寸Fig.2 Specimen size of rammed earth-timber
试件整体如图3(c)所示,包括3部分:夯土、木梁和钢模具。其中钢模具采用厚度为5 mm的钢板,钢板之间使用螺栓连接,见图3(b)。钢模具主要有两个功能:夯筑时作为成型的模板;加载时提供侧向约束。试件夯筑前,先将钢模具安装于底板上,再把土料铺放到钢模具内,每次大约铺放150 mm的高度,夯筑铁锤(图3(a))“回”字型夯筑4遍,这一层土料高度下降到铺放高度2/3左右,即可达到夯筑的要求。木梁在夯筑过程中放入夯土中,并伸入预定距离,使用水平尺确保木梁在夯筑时水平。最后把红土放满模具,夯筑后再铺夯土,反复进行,直到夯土块的高度达到300 mm。夯筑完成时需要卸下钢模具,在自然养护条件下放置3个月,见图3(d),以便夯土强度形成,并与木梁更好地粘结。待试件加载时,再组装约束钢模具。为预估试件的极限荷载,设置预试验,即试加载一个与L1同尺寸的试件。因此,实际制作9个试件。

图3 试件的制作与养护Fig.3 Preparation and maintenance of
1.2 试件材料
1.2.1 夯土 夯土材料按照福建龙岩地区红土∶砂∶水=3∶1∶1的比例调制后放入钢模具中夯筑。参考土体的无侧限抗压强度测试方法[15],制作3个150 mm×150 mm×150 mm的夯土立方块,见图4。测试得到其抗压强度分别为1.08、1.18、1.15 MPa,夯土抗压强度平均值取1.14 MPa。

图4 土体无侧限抗压强度测试试验Fig.4 Unconfined compressive strength test of rammed
1.2.2 木材 木梁采用福建杉木,在夯筑时埋入夯土,试验时其顺纹方向受拉,如图5所示。测定木材顺纹抗压强度、顺纹抗拉强度和顺纹弹性模量[16-18](试样尺寸为30 mm×20 mm×20 mm),试验结果见表2。

图5 木材顺纹材料性能试验Fig.5 Property test of timber grain lining
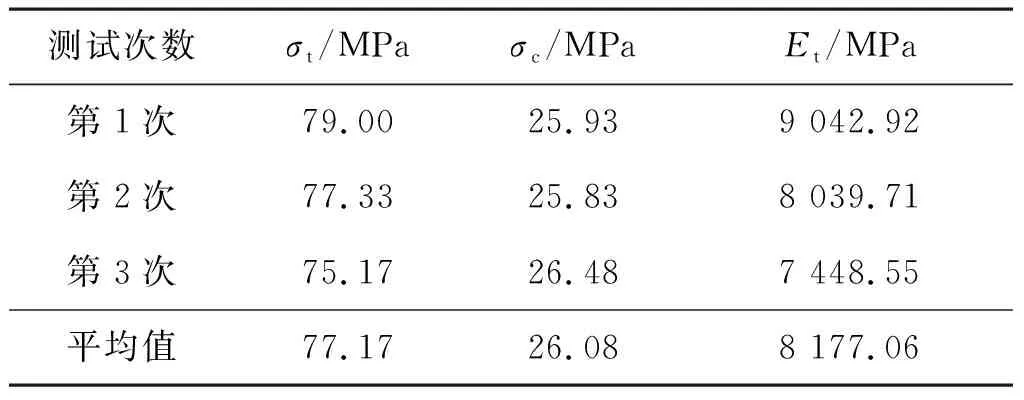
测试次数σt/MPaσc/MPaEt/MPa第1次79.0025.939 042.92第2次77.3325.838 039.71第3次75.1726.487 448.55平均值77.1726.088 177.06
1.3 试件加载
图6为加载时的现场图片。竖向压力通过竖向作动器施加,试件上部放置厚钢板以便竖向压力均匀施加在试件上。拉拔力由水平作动器提供,预先在木梁上钻孔,通过夹具与作动器连接,以便施加拉拔力。试验前根据木梁位移确定水平作动器的位置,使用水平尺保证水平作动器水平,并用滑轮在加载全过程拉住水平作动器,确保其与木梁保持在同一轴线。

图6 加载过程
试件的加载装置见图7。由于试件高度较低,受限于反力墙上的限位孔高度,需要把试件放置在预制钢架上。通过地锚螺栓把钢架、钢模具的底板及地面进行锚固;拉拔方向的两个限位装置进一步提供平面内约束;使用螺栓穿过木梁伸出侧端部的开孔与夹具固定;位移计1和位移计3分别沿着拉拔方向放置于钢模具的前后;位移计2放置于钢架一侧。位移计设置目的是校正木梁相对夯土块的位移,评估夯土块、钢架在平面内可能产生的位移对试验结果的影响。

图7 加载装置示意图Fig.7 Schematic representation of loading
预试验采用力控制加载方式,初始加载值为5 kN,荷载逐级增加1 kN。观察木梁拔出现象及位移计变化,当位移增幅较大、木梁接近滑移时,适当减小力的增加幅值至木梁产生滑移,记录极限荷载值。
正式试验参照建筑抗震试验规程[19]进行加载,采用力和位移混合加载的方式。先采用力加载方式,施加预试验得到的预计极限荷载的40%,之后每级荷载按预计极限荷载的20%增加,为保证加载后试件变形稳定,每级加载后需持荷5 min以上;达到预计极限荷载后采用位移控制加载至位移为110 mm。
1.4 测点布置
如图8所示,在木梁表面开V型槽,沿拉拔方向放置应变片,以木梁埋入与伸出位置交界处为0位置,埋入方向为正方向。埋置深度为600 mm的木梁在0、200、400、600 mm这4个位置放置应变片。埋置深度为750 mm的木梁在0、200、400、750 mm这4个位置放置应变片。每个位置左右各放一个应变片,以便测量木梁在加载时的应变变化情况。

图8 木梁应变片布置图Fig.8 Layout of strain gage for
2 模型试验结果
2.1 试验破坏形态
如图9所示,试验中主要破坏模式包括木梁拔出破坏和夯土开裂破坏。

图9 试件的破坏形态
试验的8个试件均发生木梁的拔出破坏。加载初期,木梁端的位移缓慢增大,力和位移的关系基本呈线性。随着位移的增加,木梁产生滑移并随着荷载的增大而增大。当达到力的峰值点后,荷载逐渐下降,最终趋于稳定。此时整段木梁滑移,最终发生拔出破坏。
夯土在加载过程中出现横向和纵向两种裂缝开裂破坏。在试验的8个试件中均出现垂直于木梁伸入方向的横向裂缝。在木梁滑移发展过程中,木梁伸入位置端部的夯土界面承受最大的拉力,当超过夯土的抗拉强度后,夯土截面出现横向裂缝,发生破坏。最大拉力截面随着滑移的进行而转移,所以,横向裂缝是伴随着滑移的进行而阶段性发生的,如试件L6明显出现多段横向裂缝。
在加载过程中,出现沿着木梁伸入方向发展的纵向裂缝。在木梁拔出过程中,木梁与夯土的界面逐渐产生径向裂缝,并向夯土表面扩展,当其穿透夯土后,夯土出现纵向裂缝。产生纵向裂缝的原因是在木梁拔出的时候,因其表面不光滑而引起夯土的膨胀,并在径向方向沿着夯土最少的两边发展。如在试件L2、L3、L8木梁中轴线上部的夯土出现纵向裂缝;在试件L4、L5、L7木梁两侧的夯土出现纵向裂缝。
2.2 力与位移曲线
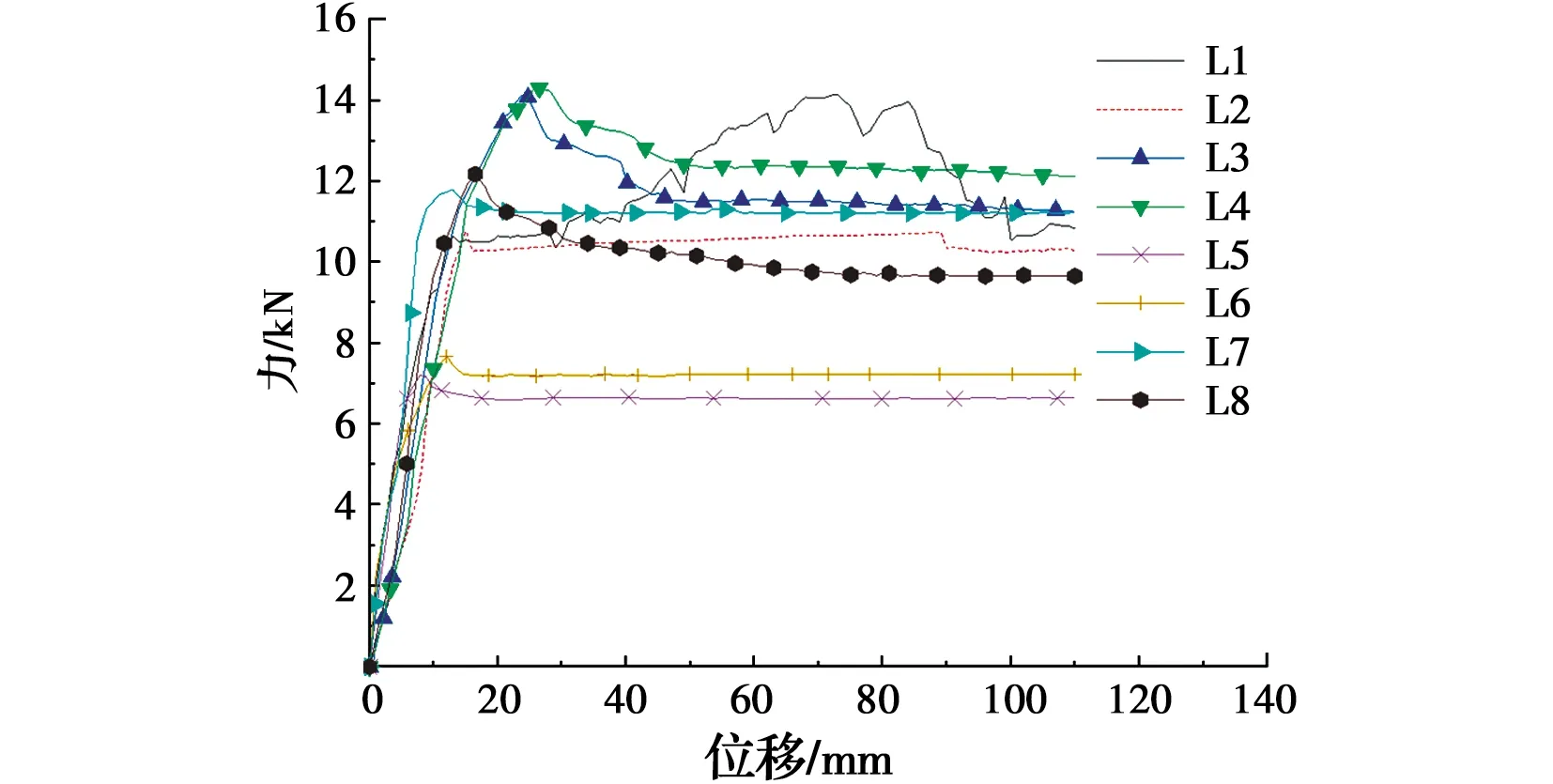
图10 拉拔力滑移关系曲线Fig.10 Load-displacement curves of all


表3 木梁与夯土墙的粘结滑移试验结果Table 3 Bond slip test results of timber beams and rammed earth walls

2.3 界面应力分布
图11为相同时刻下(即拉力相同时)木梁不同位置的应变情况。可以看出,随着埋入深度的增加,木梁的应变数值下降。当埋深以200 mm的增量从0 mm增加到600 mm时,木梁伸入长度为600 mm的试件L1、L3、L5和L7应变逐段平均减小39.1%、20.8%、28.9%。当埋深从0 mm增加到200、400、750 mm时,木梁伸入长度为750 mm的试件L2、L4、L6和L8应变逐段平均减小44.9%、23.8%、22.4%。应变逐段减小的原因是木梁通过界面将拉拔力传递到夯土中,并且随着埋深的增加,传递至夯土的力不断增加。如果埋深足够大,理论上会出现埋置浅的位置达到其粘结力极限值,埋置深的位置受力极小,甚至为零,在力和位移曲线上体现为极限荷载能够保持一段滑移距离,试验中未见此情况。

图11 木梁应变埋深关系曲线Fig.11 Strain-load relation curve of
3 有限元模拟分析
3.1 有限元模型
3.1.1 几何模型与网格划分 采用ABAQUS软件建立模型。模型由钢模具、上钢板、夯土块和木梁4部分组成。其中,木梁和夯土块的尺寸如图12所示,上钢板长×宽×厚度为1 000 mm×300 mm×20 mm,钢模具的厚度为5 mm。

图12 试件模型图
3.1.2 材料定义与求解设置 由于土的复杂性,目前还没有一种能够覆盖土所有特性的模型。现有模型都是基于土的某些特性而提出的。在ABAQUS中建立弹性与塑性本构模型,弹性模型定义夯土的弹性模量以及泊松比,Mohr-Coulomb模型主要适用于在单调荷载下的颗粒状材料,参数简单明确,适用于本文中土的模型。根据相关夯土材料性能的测试[20],输入夯土材料参数,见表4、表5。

表4 弹性参数Table 4 Elastic parameters

表5 塑性参数Table 5 Plastic parameters

钢模具与上钢板的弹性模量比生土和木材大3个数量级,计算变形忽略不计,按照弹性材料模拟。
分析步采用Static General静力求解器,对耦合了端部截面的参考点创建场变量输出,以便观测其力和位移情况。
3.1.3 相互作用与边界条件 夯土与钢模具的接触使用“硬接触”的正向模型和无摩擦的切向模型。上部厚钢板与夯土进行绑定设置,没有相对运动。建立一个参考点,与木梁伸出段前端进行耦合,通过查看参考点的力和位移曲线来验证模型的正确性。


图13 界面连接器


图14 荷载与边界
3.2 模拟分析结果
3.2.1 力和位移曲线 如图15所示,对8个试件的试验过程进行模拟,得到计算拉拔力和位移关系曲线,并与试验测试结果比较。从两个试件的力和位移曲线来看,模拟与试验的曲线走向基本相同,具有线性上升段、滑移过渡段和摩擦残余段。计算与试验曲线的极限荷载和滑动摩擦力较吻合,峰值滑移存在差异,但总体变化趋势相符,如表6所示。

表6 试件模拟和试验结果比较Table 6 Comparison of specimen simulation and test results

图15 拉拔力滑移关系曲线比较Fig.15 Comparison of load-displacement
3.2.2 木梁粘结滑移 图16(a)是木梁拉拔方向的应力分布情况,A端为木梁远离夯土的一端,位置记为0 mm。8个试件的木梁沿伸入方向的应力变化如图16(b)所示,木梁在起始位置(A端)的应力最大,这是因为此端为加载端,出现应力集中,导致应力偏大。随后出现平缓段,为木梁伸出夯土段。当夯土与木梁接触后,应力发生变化,且随着伸入距离的不断增加,应力逐渐降低,最终在木梁伸入端部(B端)下降至最小。

图16 试件木梁的应力分布Fig.16 Stress distribution of wood beam of


图17 L3试件木梁的不同位置的应力位移图Fig.17 Stress-displacement diagram of wood beam of L3 specimen at different


图18 试件夯土应力图Fig.18 Stress diagram of rammed
4 粘结力计算方法
4.1 界面粘结力组成


4.1.1 胶结力 在加载初期,胶结力起主要作用。试验采用的福建红土本身含有较高比例的黏土,经过3个月的养护后,夯土与木梁表面有效粘结在一起。胶结力在木梁滑移的过程中逐步消失,直到下降为零。
随着拔出力的逐渐增大,胶结力破坏,木梁有滑移的趋势,木梁与夯土之间的摩擦力开始发挥作用。待荷载达到最大静摩擦时,界面承载力开始下降,此时达到极限荷载值,胶结力快速下降,界面完全依靠滑动摩擦力起作用。
4.1.2 表面摩擦力 表面摩擦力在加载的全过程都起作用。界面达到极限滑移荷载时,静摩擦达到最大值,木梁开始滑移,此时主要受滑动摩擦力影响。
夯土所受的竖向压力提供摩擦力的正应力。对夯土施加竖向压力时,夯土有向周围膨胀的趋势,但受到钢模具的约束,相当于钢模具对夯土施加压力,使得夯土处于三向受压状态。在这种情况下,夯土对木梁的压力为表面摩擦力提供正应力。

4.2 粘结滑移关系
所有试件的力和位移曲线都具有统一的形状特征,可分为线性上升段、滑移过渡段和摩擦残余段3部分,如图19所示。第Ⅰ部分,曲线呈线性增长,胶结力缓慢降低;第Ⅱ部分,出现明显的非线性行为,胶结力快速降低,当达到最大静摩擦后,粘结力开始下降;第Ⅲ部分,木梁完全滑移,胶结力完全消失,界面存在滑动摩擦力与基质吸力,曲线斜率趋近于零,粘结力达到稳定。
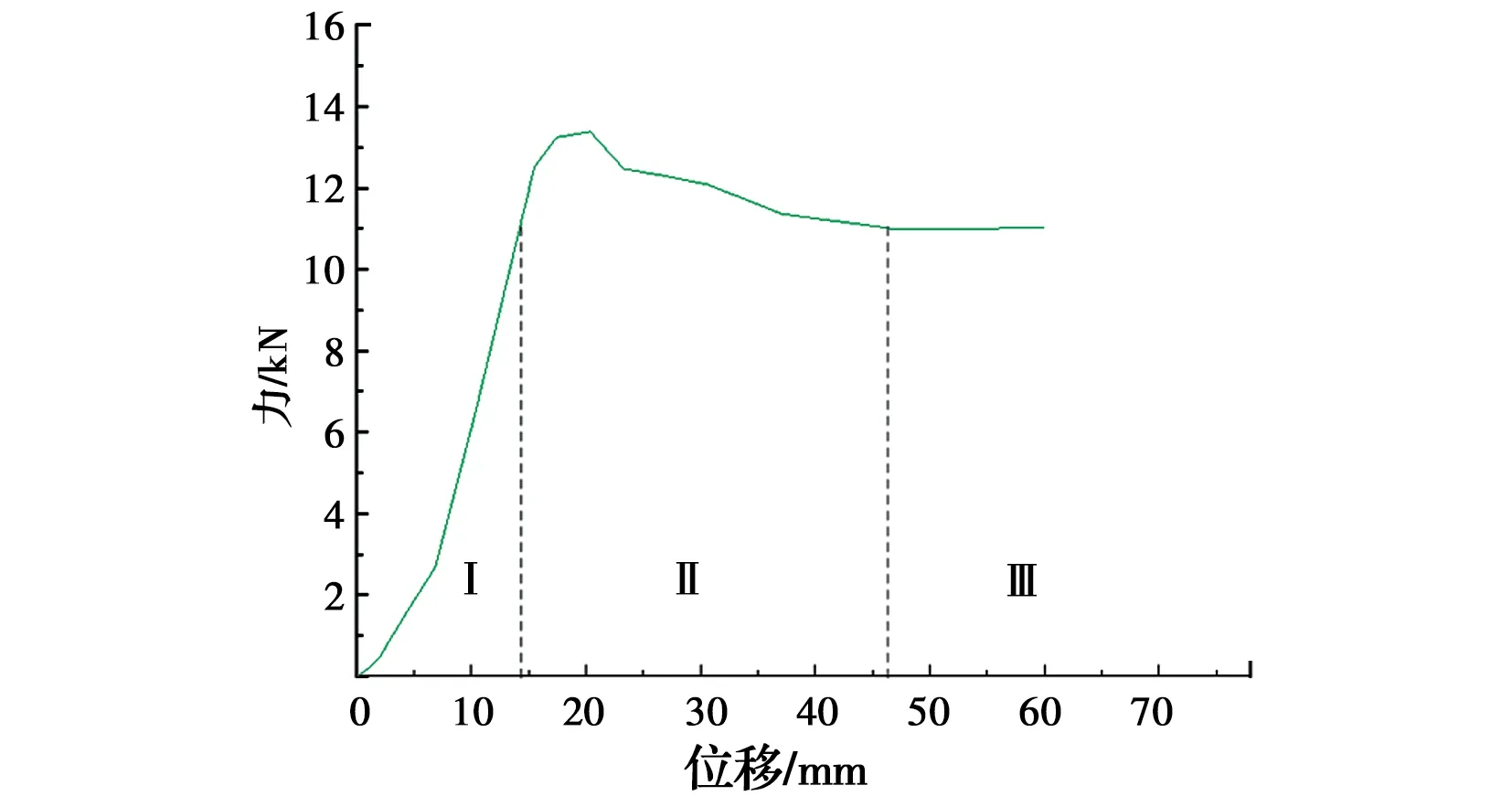
图19 L3试件的3段式力位移曲线Fig.19 Three-stage force-displacement curve of specimen
4.3 粘结力计算式
Fuls=F0+FN+F(u)
(1)
式中:F0为部分胶结力;FN为表面摩擦力;F(u)为基质吸力。
部分胶结力F0在达到极限滑移荷载之后逐渐消失为零,其数值为每个试件的极限荷载与摩擦残余段荷载的差值。
根据Vanapalli等的研究[25],表面摩擦力FN和基质吸力F(u)构成摩擦残余段,可分别表示为
(2)
式中:σv为压应力,即夯土竖向压力对界面施加的压应力;δ为界面摩擦角;ua-uw为基质吸力,其值通过测得含水率并对照SWCC曲线得到;Sk为有效概率,土的饱和程度和含水率有关;δ′为有效表面摩擦角,为夯土内摩擦角的1/3~2/3;πdL为木梁的表面积,其中d为木梁直径,L为木梁伸入长度。
使用前述有限元模型,木梁和夯土界面接触使用“硬接触”的正向模型和摩擦的切向模型,施加10、20 kN的竖向荷载,探究木梁的伸入长度为600、750 mm时的摩擦力以及摩擦系数的关系,见图20。在其他因素不变的情况下,摩擦系数和摩擦力是线性关系。通过图20与表3的数值对比,确定试件的粗糙摩擦系数为0.6、光滑摩擦系数为0.1,摩擦系数与摩擦力见表7。

图20 摩擦系数与摩擦力的关系Fig.20 Relation between coefficient of friction and

表7 竖向压力提供的摩擦力数值Table 7 Friction value provided by vertical pressure
在摩擦残余段,FN和F(u)共同起作用,基质吸力F(u)可表示为摩擦残余段荷载与表面摩擦力FN的差值。试件粘结力Fuls的各组成部分见表8。

表8 试件各部分界面力组成Table 8 Interface force composition of each part of the specimens
5 结论
1)试验试件发生木梁拔出破坏和夯土开裂破坏。木梁拔出破坏在8个试件中均有发生。夯土发生开裂破坏时,横向裂缝出现在木梁伸入端部位置,并随滑移的增加而阶段性发生;纵向裂缝出现在木梁中轴线上部和木梁两侧的夯土上。



