基于模型预测的日光温室温度优化控制

杜太行，刘 德，孙曙光，钱春阳,2，梁倩伟

(1. 河北工业大学人工智能与数据科学学院，天津 300130; 2. 天津市农业科学院信息研究所，天津 300192)

0 引 言

日光温室是我国北方主要的特征温室，应用广泛。温度是绿色植物生长发育、新陈代谢等生命活动的重要环境条件，因此温度控制是现代化温室管理的首要任务[1]。日光温室室内温度较高时打开风口降温，当温度持续升高时关闭风口打开风机进行机械通风，这种以输入量为开关量的切换控制在温室中较为普遍。开关控制具有设备价格低、易操作以及易维护等优点，但同输入为连续量的系统相比，开关量控制系统的温室小气候环境控制难度更高[2]。近些年，国内外许多专家学者针对温室小气候控制，进行了深入的研究。模糊控制、专家系统控制都依赖于生产经验[3-4]，且作用于被控制对象都是连续的输入控制量，对于输入为开关量的温室系统难以取得较好的控制效果。文献[5]针对离散开关量控制的温室设计了混杂控制器，其本质仍是基于事件触发的切换控制，控制的有效时间短、效率低。文献[6]设计了开关组合的预测控制，克服了温室系统的时滞问题，但设计的预测模型过于简单难以适应环境复杂多变的温室。上述方法均未考虑到控制过程中执行设备是否切换过于频繁以及设备能耗问题。文献[7]通过遗传算法确定了温室机理模型未知参数，建立了精确的预测模型，同时将能耗和水耗目标引入预测控制中，但建模的过程较为复杂。

本文在现有研究理论的基础上，提出了基于模型预测（model predictive control, MPC）的日光温室温度优化控制方法。通过神经网络来建立温度的灰箱预测模型，克服温室建模复杂的问题。在日光温室夏季温度的4种开关量控制切换中，通过引入模型预测控制思想建立以温度的控制误差、设备切换次数、系统能耗为优化条件的目标函数。该控制方式主要侧重于未来局部控制时域内控制性能最优。最后，在实验现场对基于模型预测的温室切换系统进行验证。

1 温室温度预测模型构建

在实现模型预测控制时，首先要建立对象的数学模型，然后收集实时数据，根据模型来预测被控对象的运行状况。日光温室是一个非线性、强耦合、时变的复杂系统，很难建立准确的数学模型。针对温室的上述特点，采用在非线性模型的长时域多步预测中有良好表现的NARX神经网络预测未来时刻温室室内温度。以外界环境输入量、温室控制状态量、室内温度共同作为神经网络的输入，未来时刻的室内温度作为输出，建立预测模型。

1.1 温室简介与数据处理

实验温室位于天津市北辰区，由天津农科院提供，是典型的北方日光温室。温室结构见图1，温室坐北朝南，长约 70 m，宽 6 m，脊高 3.5 m，占地面积约为420 m2。温室支撑材料采用的是铝合金，覆盖的透光材料为加厚的聚乙烯薄膜，日光温室在夏季共有4个控制状态，均为开关量输出，分别为保温、自然通风、机械通风、风机-湿帘状态，它们的降温能力依次增强，同时消耗的能量也依次增强，温室在这4个状态中进行切换达到降温的目的，如表1所示。

图1 实验温室结构示意图

表1 温室控制状态

根据现代温室的需求设计了现场温室环境监测系统，在温室现场布置的各类传感器采集环境信息为控制决策提供依据。温湿度传感器的型号为SHT35，测量太阳辐射的传感器和风速风向一体传感器分别为仪谷公司生产的YGC-TBQ和YGC-FX，测量时间间隔为1 min。传感器数据的准确性是模型有效的先决条件，传感器采集环境因素时，可能会出现电磁干扰、通信错误等问题，导致测得的数据会有较大的偏差，因此需要对传感器采集的数据进行处理。

1.1.1 异常数据剔除

对于偏差较大的测量数据，应给予剔除。采用3σ 准则：对于样本数据X={x1,x2,···,xn}，其标准差为：

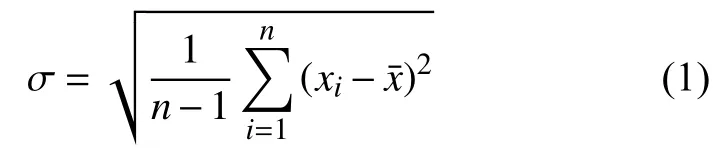
1.1.2 缺失数据插补

将粗大误差数据剔除后，会导致数据缺失，为了保存数据的完整性，采用KNN插补算法补全数据。该算法的思想是利用缺失数据项和完备数据项之间的相似性来选择插补数据集合，设两个数据样本i,j，采用欧氏距离的两个样本之间的相似度衡量表达式为：

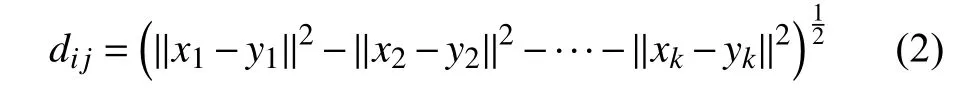
KNN插补算法的执行步骤如下：

1)设置最大邻近数目K。

2)选取数据集中含缺失数据集的D1和不含缺失数据集的D2。

3)对于每一个数据样本，D2中求取K个最邻近数据项，根据式（2）取对应的距离度量函数，对应的di缺失数据为

4)将di加入到D2。

5)重复步骤3)，直至D1为空集。

1.1.3 数据归一化

采集的各个环境因素量纲不同，数量级差别较大。数据直接用于温室预测模型的建立，会影响模型的精度。对采集到的输入输出数据进行归一化处理，如下所示：

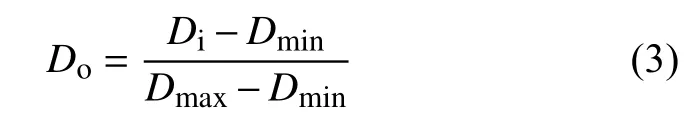
其中Dmin、Dmax分别为同一环境因素中的最小值和最大值。

1.1.4 模型的室外输入变量选择

2020年8月30 日至9月7日测量的室外的辐射强度、温度、风速、湿度的环境原始数如图2所示。

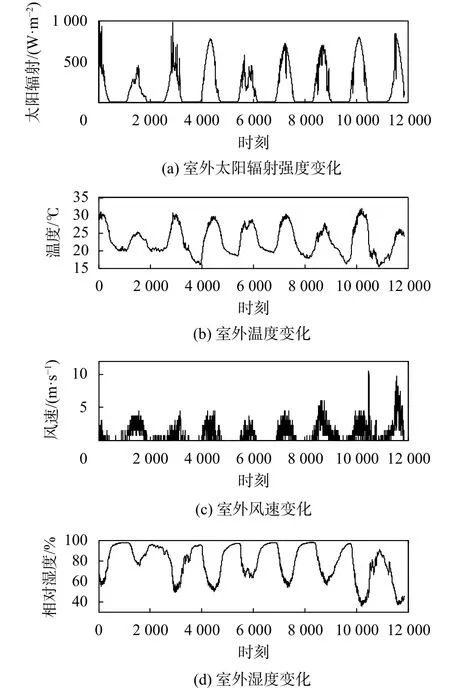
图2 室外环境因素变化

由于室外环境因素对室内温度影响程度各有不同，因此选取合适的环境因素作为预测模型的输入尤为重要。采用皮尔逊相关系数进行相关性分析，选取与室内温度相关性较高的室外环境输入量，公式如下：

式中：X，Y——求取相关性的两个序列；

E(X)、E(Y)——X，Y两个序列的期望。

代入图2 所示的实验期采集数据计算相关性，结果如表2所示。

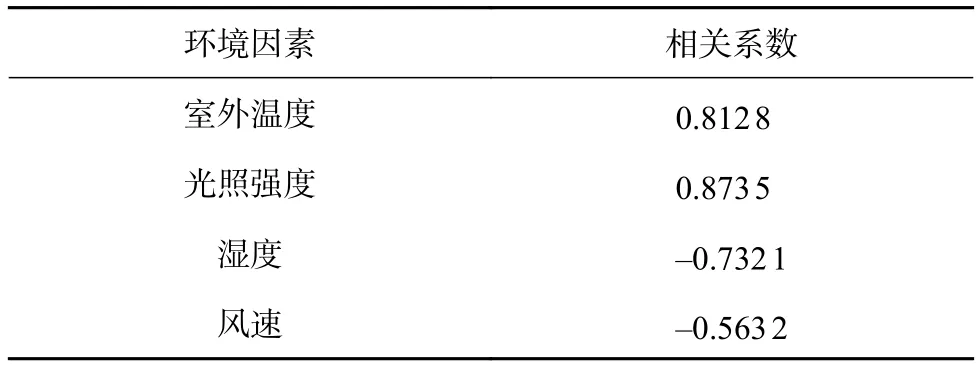
表2 室外环境因子与室内温度相关性

通过表2，确定外部环境输入量为室外温度、光照强度、湿度、风速。

1.2 NARX温度预测模型

NARX神经网络是一种非线性带外输入自回归模型，且具有记忆功能。它通过一个延时器记录最近几次外部输入和输出，包含了多步输入输出的时延[8-9]，同时加入了反馈机制，因此增强了对历史数据的记忆能力，具有动态存储功能，是一种动态神经网络。因此，NARX适用于时间序列预测，并被应用于解决多种领域的非线性序列预测问题。模型结构如图3示。

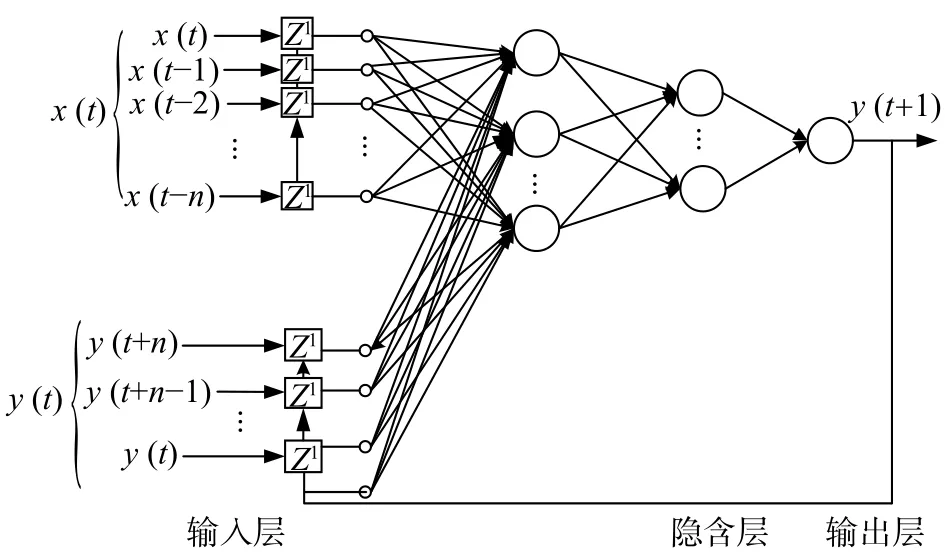
图3 NARX神经网络结构图

NARX采用三层神经结构，即输入层、隐含层输出层[10]。输入层向量为室外温湿度、光照强度风速、温室控制状态量以及室内的温度，输出量为室内温度未来时刻的预测值。

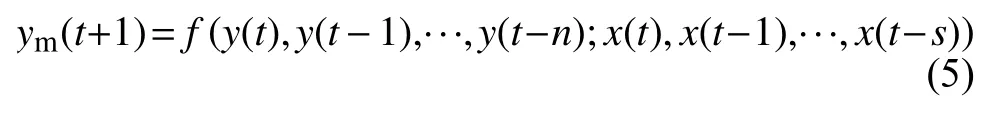
式中：f——非线性函数；

x(t)、y(t)——模型输入量；

ym(t+1)——预测输出；

n，s——外部输入和自输入滞后的阶次。

1.3 模型检验

模型检验为定量描述预测模型精度，验证模型输出与实际输出效果提供了依据。采用均方根误差、最大绝对误差、拟合优度作为评价指标，如下所示：

式中：n——测试样本数目；

yi(k)——系统实际输出；

ym(k)——模型的预测输出；

均方根误差、最大绝对误差越小模型精度越高，拟合优度与之相反。

2 温室模型预测控制算法

温室的MPC系统由预测模型、滚动优化、反馈校正三部分组成[11]。温室的模型预测控制是将温室的温度控制问题转化为目标函数求解最优值的问题，控制流程见图4。

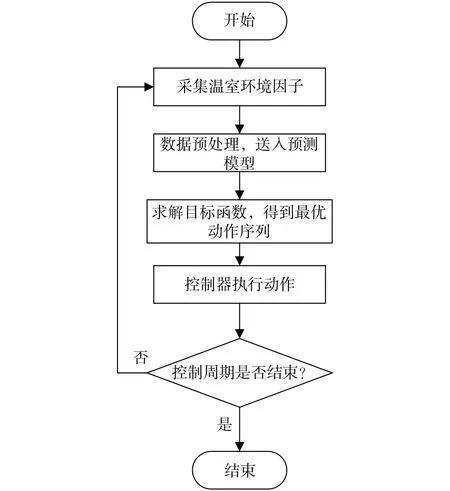
图4 温室预测控制流程图

2.1 目标函数的建立

日光温室夏季调温的方法是让温室在4个不同的控制状态进行切换，MPC控制策略是使室内温度接近给定目标温度，保证温室内作物处于合适温度区间，同时，最大限度地降低控制时域内能耗的成本和执行机构切换的频率，构建的目标函数如下：

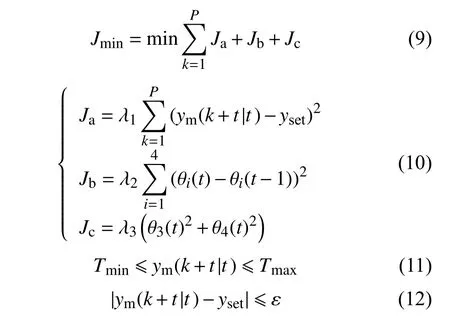
式中：Jmin——目标函数；

Ja——输出值跟随目标值；

Jb——约束设备切换频率；

Jc——约束风机和湿帘两种设备的运行时间，因为这两种设备是温室产生能耗的主要来源；

λ1，λ2，λ3——各个状态约束的权重系数，改变该参数可以调节系统的性能；

θi(t)——t时刻温室第i个控制状态量，其值为 0或 1；

Tmin、Tmax——室内温度设定的最小值和最大值；

ε——一个极小的正数值；

P——控制步长；

yset——控制的目标值。

2.2 滚动优化与反馈校正

每求解一次目标函数，便得到一组控制序列。若将得到的输出序列全部作用于系统，下一时刻的测量值将无法影响控制器动作，即测量值所包括的外部干扰或模型误差信息得不到有效利用[12-13]。滚动优化的方式就是将每个采样时刻的最优控制序列的第一个控制量作用于系统，在下一个时刻，继续将这一时刻的优化解的第一个控制量作用于系统，这样重复至无穷。

温室每更新一次当前状态，预测模型都以当前时刻状态量为输入，即使上一个时刻预测误差较大，也不会对下一次预测产生影响。但随着时间的推移，离线的神经网络的输出可能会有较大的偏移，需要重新训练模型。为此设计一个智能监督级，作为控制系统的反馈校正环节。

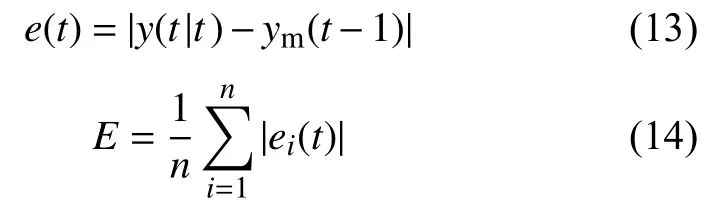
式中：e(t)——当前时刻t模型的预测误差；

y(t|t)——当前时刻的实际值；

ym(t–1)——模型对当前时刻的预测值；

E——平均误差，当达到设定阈值时，更新预测模型。

2.3 MPC算法实现步骤

采用MPC对日光温室系统进行控制，考虑了系统输出跟随给定目标值、执行机构切换的频率以及控制过程中的能耗。模型预测控制得出的控制结果是基于目标函数得出的最优结果，系统的输出结果不一定是全局最优，却是当下系统预测时域内最优的输出结果，预测轨迹为一段温度区间，控制框图如图5所示。

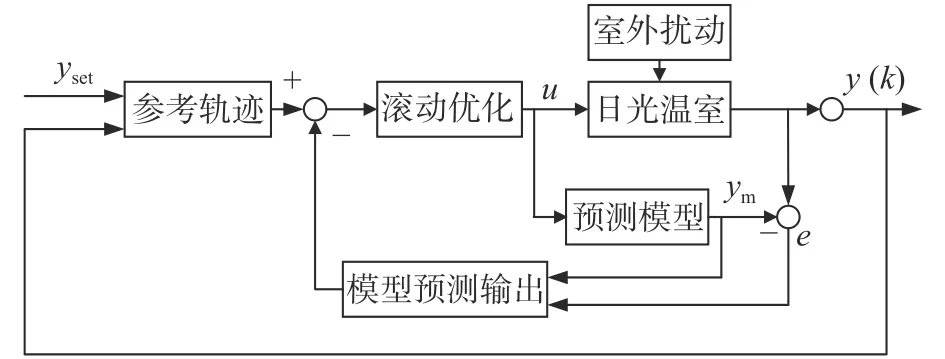
图5 MPC的控制结构

MPC算法具体执行步骤如下：

1)系统初始化，采集当前时刻室外环境因素、室内温度、设备运行状态，确定系统的初始状态，设定目标控制值yset。

2)将当前时刻采集的数据信息送入NARX预测模型，以滚动的方式计算当前时刻t对未来预测时域N内的温度预测序列

3)把上一时刻模型对当前时刻的预测值同当前时刻实际的温度值作差，得到此时的预测误差e。

4)以室内温度偏差、切换频率、能耗最小为目标函数，对室内温度进行P步预测控制，每一步都有4种操作可以执行共有4P组操作序列。当基数不大时，可用遍历的方式筛选出使得目标函数最小的一组控制序列。

5)将求得的控制序列 [u1,u2,···,un]的第一个控制量作用于温室系统，重复上述步骤。

3 日光温室控制实验分析

3.1 NRAX预测模型效果分析

执行机构的动作周期过长，会导致控制系统反应过慢难以进行及时的修正。执行周期过短，则会导致控制系统产生大量的在线优化计算以及执行机构频繁操作。考虑温室每次降温到达稳态的时间规定执行机构最短的动作时间为5 min，故规定预测模型的一步预测时间为5 min。

将2020年8月31日至9月6日采集的实验数据作为训练集训练模型，后一天采集的数据为测试集，验证预测模型的准确性，温室的一步预测和三步预测结果，见图6和图7。

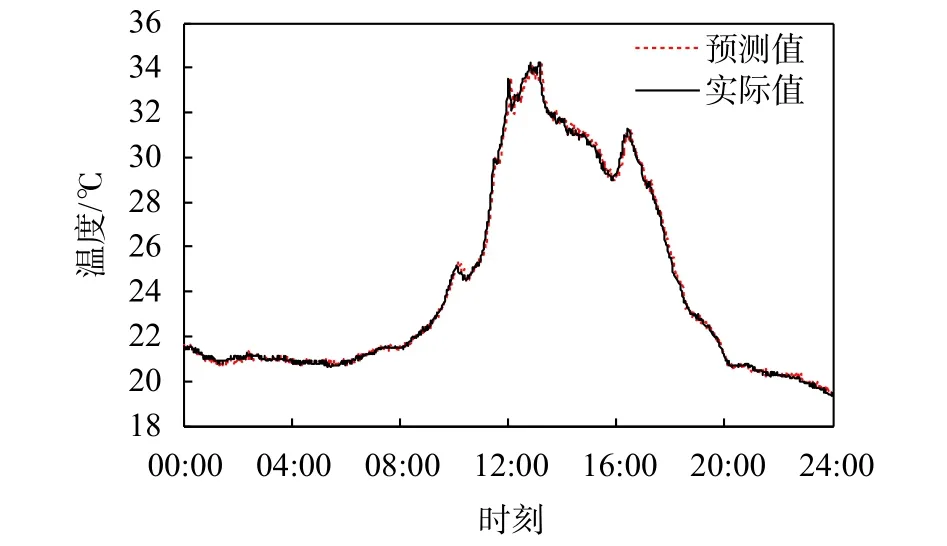
图6 室内温度一步预测

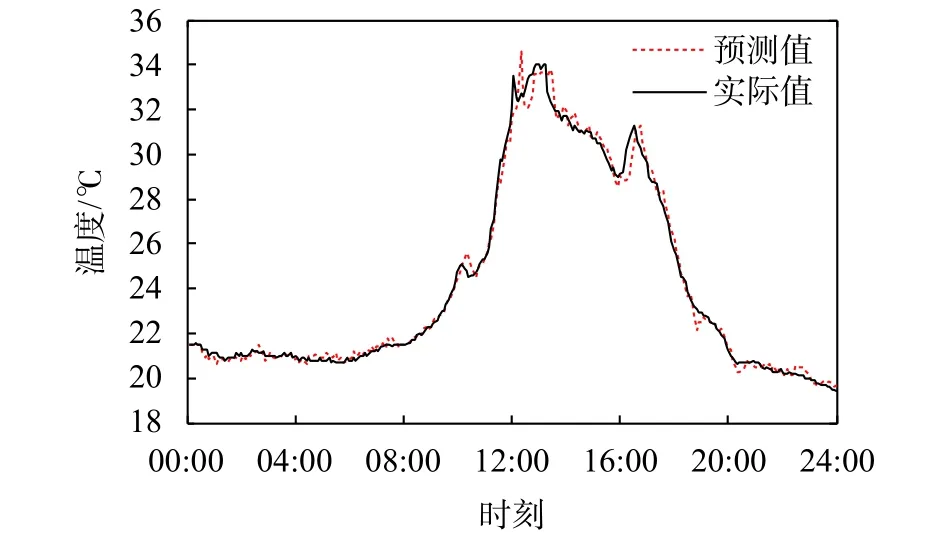
图7 室内温度三步预测

从图中可看到预测曲线和实际曲线基本吻合，该模型预测效果较好。不同步长下室内温度预测结果如表3所示。

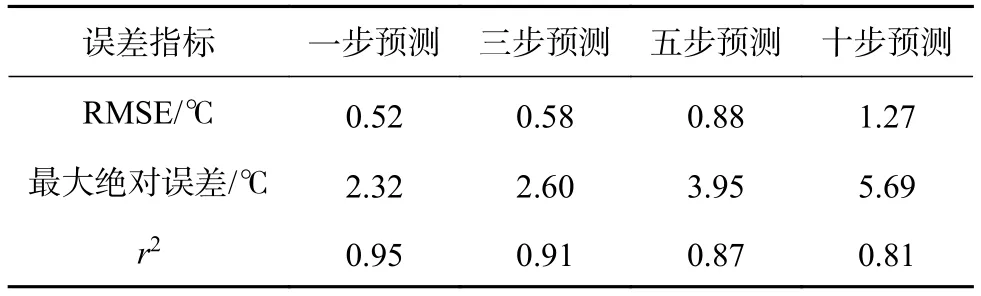
表3 预测结果

观察表3，可知在三步预测范围内最大绝对误差分为2.6 ℃，均方误差为0.58 ℃，都在误差允许的范围内。在五步预测时最大绝对误差达到3.95 ℃，模型精度明显下降，该误差结果已经会对预测控制产生较大的影响。上述结果表明：在三步预测范围内预测模型能够较好地预测未来室内温度，满足预测控制需求。

3.2 MPC控制效果分析

实验期间室内种植作物为网纹甜瓜，处于结果期，昼间设定控制区间为 [25 ℃，30 ℃]，最优的温度为 27 ℃，夜间控制区间设定为 [15 ℃，20 ℃]，最优温度为17 ℃。设计基于事件触发的切换控制规则，如图8所示。

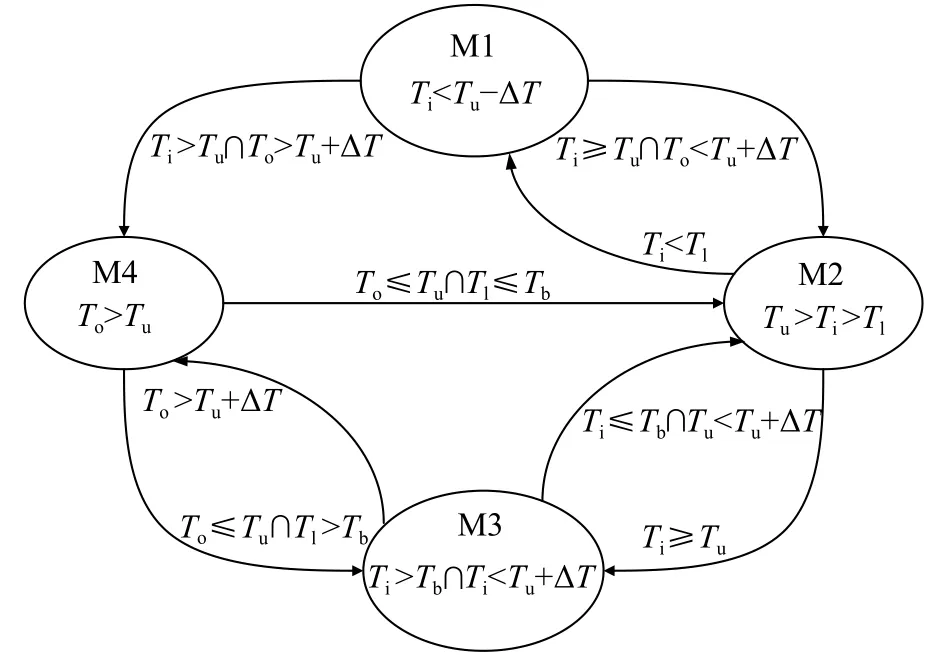
图8 温室切换控制状态转移

图中 ΔT为防抖温度，Ti为室内温度，To为室外温度，Tb为最优温度，[Tl,Tu]为温度控制区间。将上述控制规则写入温室现场监控软件，控制结果如图9所示。

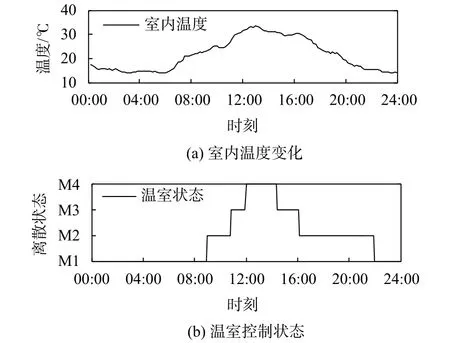
图9 传统切换控制下的结果

从图9中可以观察到当室外温度上升时，室内温度持续攀升。夏季午后室内外温度达峰值，该方法具有滞后性，导致室内前期蓄热过多，且温室内的降温设备的降温能力是有限的，即使此时采用风机-湿帘组合，室内温度依然无法降到目标区间内。

在同样的目标区间下，采用模型预测控制。目标函数计算量与控制时域步数P成指数关系，考虑预测模型的有效预测范围目标函数的计算复杂度，确定P=3。在15 min内最多执行3次操作，共64组操作序列。采用遍历的方法求解目标函数的最小值，控制结果见图10。

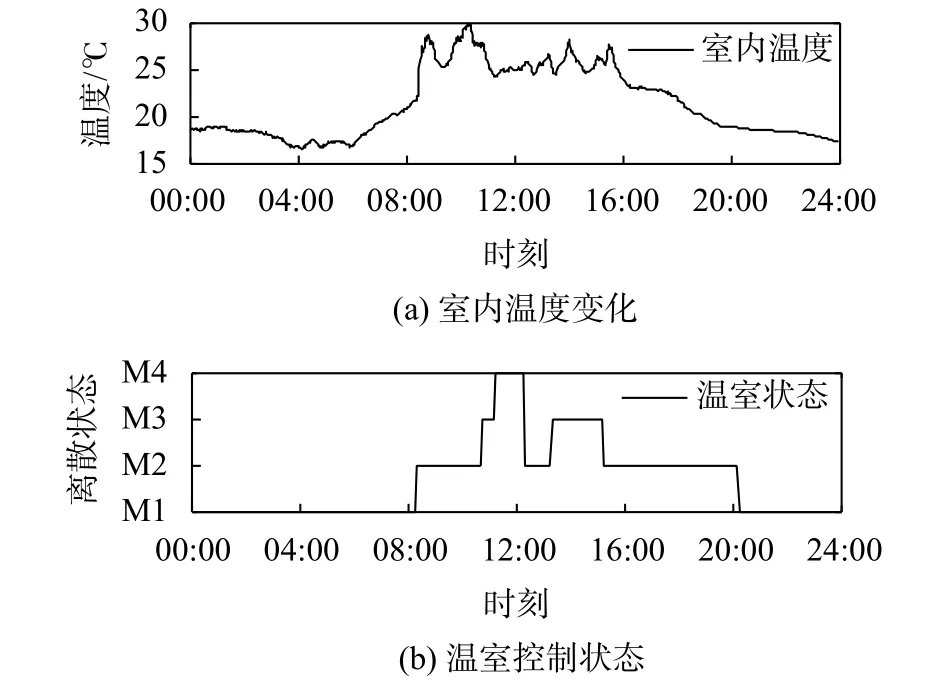
图10 模型预测控制下的结果

实验期间室外最高温度为31.9 ℃，室内最高温度为29.7 ℃。由于前期风机湿帘组合较早启动，温室没有蓄热，所以整体的温度控制比较平稳，两种控制方式对比结果见表4。

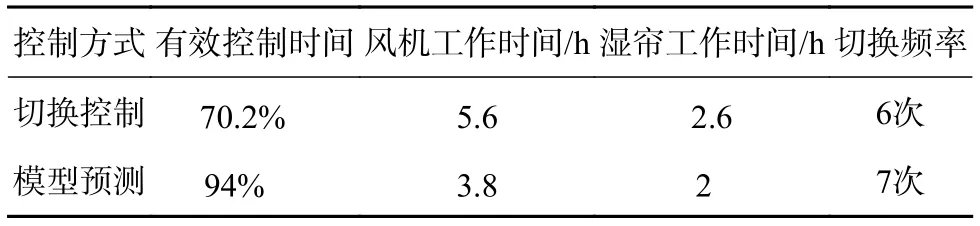
表4 两种控制方式对比结果

通过模型预测控制温室内的平均温度下降了1.2 ℃，有效控制时间提高23.8%，最耗费能量的两种设备的使用时间都明显降低，故系统节能的效果显著，整个过程中系统切换次数仅提高了1次，并未造成设备的频繁开启。

重新设定目标区间，昼间设定控制区间为[25 ℃，28 ℃]，最优温度为26 ℃，夜间控制区间保持相同。采用MPC得到的控制结果如图11所示。

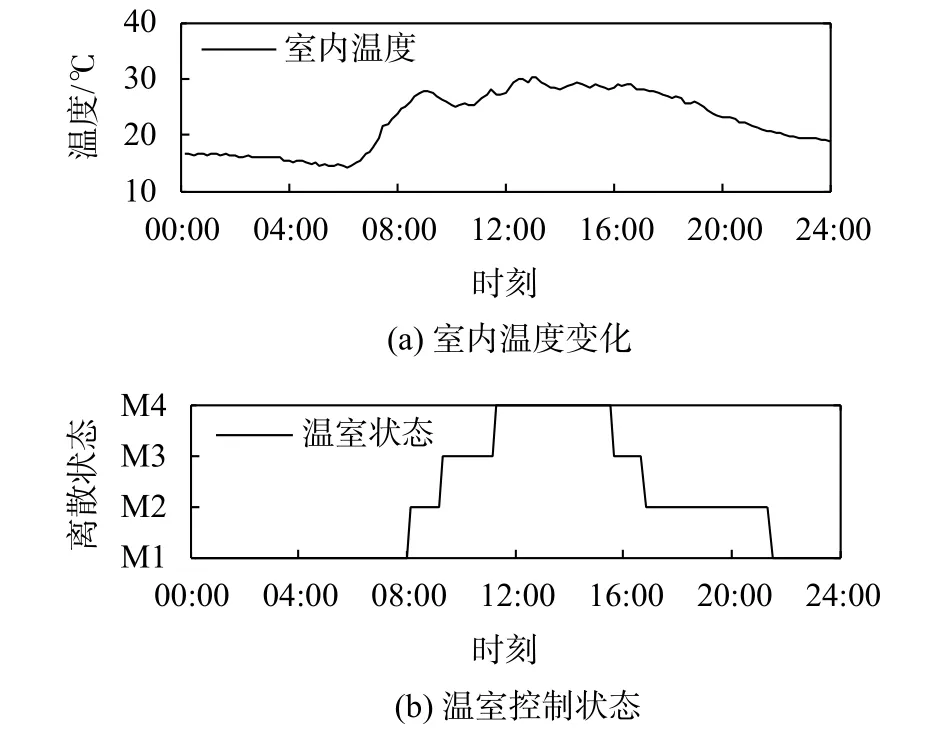
图11 短区间模型预测控制下的结果

缩短了温度控制区间后，室内最低温度为14.1 ℃，最高温度为30.3 ℃，对比图10温度波动更加平稳，但有效的控制时间为75%明显下降。为了快速降温风机和湿帘组合启动的时间也提前了，且持续工作时间更长。从能耗的角度考虑，选择合适的控制区间能够为温室节约能量。

为了进一步验证模型预测控制算法的有效性，将MPC控制算法同模糊控制进行对比，模糊控制依赖管理经验且仅依据当前温度值进行调控。2020年9月10日与9月11日两天的天气状况相近进行对比实验，控制结果如图12所示。

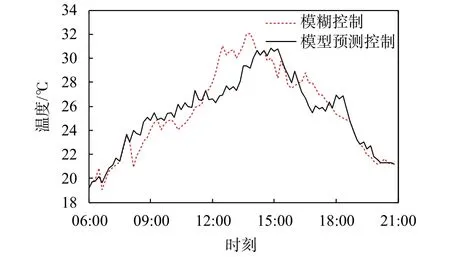
图12 两种控制方式下室内温度变化

由控制结果可以得出：基于MPC的温度控制果明显优于模糊控制，前者温度上升稳定，变化幅度较小，后者的温度上升较快有效控制时间更短。这说明采用模糊控制时，温室的状态不会及时变化，后续的室内温度变化也无法提前预测，只有在温度过低或过高时才开始控制。由于在MPC策略中具有独特的多步预测和动态滚动优化功能，因此控制效果更好。

4 结束语

本文针对传统控制方法在开关设备温室系统中有效控制时间短、能耗高等问题，提出了基于MPC的日光温室优化策略，建立了室内温度的NARX滚动预测模型，通过求解目标函数得到局部时间内的最优控制。通过连续试验表明，本系统稳定可靠，室温基本可以稳定在设定的区间内，对比传统切换控制和模糊控制有效时间均有所提升，且有效降低了温室的能耗，提高了经济效益，较好地满足夏季日光温室的生产需要。本文工作还存在进一步深化的内容：MPC方法中，目标函数约束条件中权重系数λ可以调整经济性能和控制精度间的比重，各权重系数如何更好地分配，在未来的研究中将继续探讨。