大规模可再生能源接入区域电网侧储能频率稳定控制方法研究

谢永胜，王凡，胥国毅，王衡

（1.国网新疆电力有限公司，新疆 乌鲁木齐 830000；2.华北电力大学新能源电力系统国家重点实验室，北京 102206）

0 引言

传统电网中的同步发电机具有良好的惯性和阻尼特性，能够通过惯性响应吸收或释放能量，维持系统频率稳定[1]。大规模可再生能源通过电力电子设备并入电网，但无法为电网提供稳定、有效的惯量支撑。电力系统正向低惯量的方向发展[2]，由惯量降低而引发的电力系统频率稳定问题逐步引起关注[3]。

随着储能价格的降低和可再生能源发电对储能需求的增大，储能技术得到了迅猛发展，其应用场景涵盖电力系统“发-输-变-配-用”各个环节。电网侧储能主要面向电网调控运行，被广泛用于平滑风电场有功出力抑制风功率波动、补偿可再生能源系统的虚拟惯量等环节，大大地改善了风光等可再生能源的运行特性[4]。利用储能单元的充放电来模拟传统同步发电机的频率响应能力，使储能单元具备与同步发电机相似的外特性[5]，将在很大程度上解决可再生能源大规模接入面临的频率稳定问题。

目前，储能提供虚拟惯量的技术路线按照惯量源响应特性及控制方式可分为电流源型虚拟惯量和电压源型虚拟惯量控制[6]。电流源型控制将系统的频率变化率（Rate of Change of Frequency，ROCOF）引入有功控制环节，使储能向电网提供与频率变化率成正比的附加功率。电流型控制本质上仍是功率源，与同步机组的转动惯量有本质区别，不具有分担系统功率扰动的能力[7]。电压源型虚拟惯量主要指虚拟同步发电机（Virtual Synchronous Generator，VSG）技术[8]，[9]。在变流器控制环节引入同步机转子运动方程及电磁暂态方程，使其具有与同步机组类似的惯性和一次调频特性，能够在扰动初期承担部分扰动功率。文献[10]提出一种基于自适应的VSG控制策略，该方法模拟同步发电机的行为，构造频率变化率与虚拟惯性的关系，自适应改变虚拟同步发电机控制的惯性，从而提高微电网系统抗干扰能力和过载能力。文献[11]分析了同步发电机和虚拟同步机的频率响应特性，探讨了虚拟同步机的虚拟惯量与阻尼配置问题。上述对储能/可再生能源虚拟惯量控制的研究，大多聚焦于控制策略自身的频率响应特性，一般在微网或无穷大电网中实现，大多不考虑其对实际电网的影响，且频率控制策略考虑单一，缺少控制策略间的性能对比，不利于根据实际电网的需求选择恰当的频率控制策略。

对电力系统进行频率响应特性分析、获得频率响应曲线是研究不同储能控制策略对实际电网频率支撑能力的前提。电力系统频率响应分析方法包括时域仿真法和等值模型法[12]。时域仿真法模型详细，能够较为准确地获得实际电网的频率响应[13]，但受限于时域仿真软件的功能，尚无法灵活实现各种储能频率控制策略，在不同虚拟惯量控制策略对实际电网的频率支撑能力对比中难以应用。以电力系统频率响应模型（System Frequency Response，SFR）为代表的等值模型法，能够灵活实现各类可再生能源频率控制策略，并且具有模型阶数低，运算速度快的特点，但由于模型过于简化，对于实际大电网的频率响应分析精度较低[14]，[15]。

本文基于灵敏度分析不同频率响应指标的主导参数，明确高比例可再生能源接入对系统频率响应指标的影响规律，建立了改进的计及储能频率控制的频率响应模型，并以新疆南疆地区电网为算例，对比不同技术方案的频率控制效果，有利于根据电网的实际需求选择储能频率控制方案和频率控制参数。

1 系统频率响应指标主导参数分析

频率控制参数直接决定系统的频率响应特性，主导参数对系统频率响应指标的影响更大，因此明确关键参数在频率响应不同阶段的作用，有利于根据实际电网的调频需求合理选择频率控制策略。轨迹灵敏度指系统参数发生微小变化时系统动态轨迹的变化程度，能反映系统的时域轨迹与参数的关系[16]。通过求解各参数对系统频率偏差的轨迹灵敏度，可以确定影响系统各频率响应指标的主导参数。本文利用SFR模型[17]求解参数的轨迹灵敏度，其传递函数如图1所示。

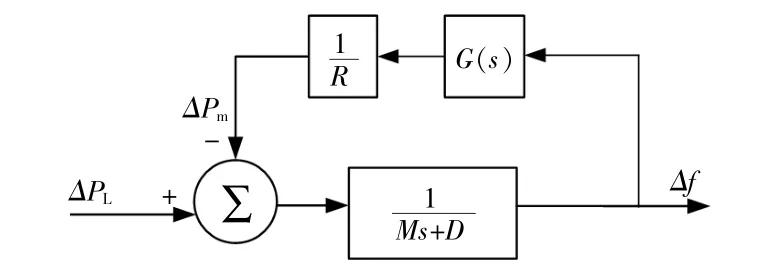
图1 SFR模型Fig.1 SFR model

图中：ΔPL为功率不平衡量；Δf为频率偏差；D为等效阻尼系数；M为等效惯性时间常数；G（s）为原动机传递函数；R为调差系数，表示同步机组调速器作用。实际系统中原动机的特征参数通常为固定值，因此影响系统频率响应特性的主要参数为调差系数R、惯性时间常数M和等效阻尼系数D。

各参数的绝对灵敏度为系统频率偏差对该参数的偏导，即：

为获得更明显的频率偏差，ΔPL取0.5 p.u.。设系统最大频率偏差出现时刻为Tnadir，各参数的轨迹灵敏度曲线如图2所示。

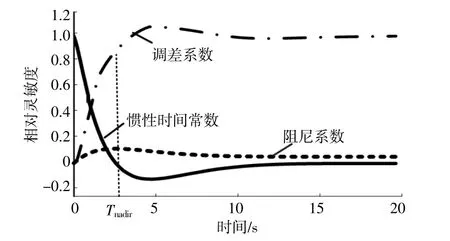
图2各参数轨迹灵敏度曲线Fig.2 Trajectory sensitivity curves of different parameters

由图2可以看出：在频率变化初始阶段，频率变化率对惯性时间常数的灵敏度最大；随着时间推移，惯性时间常数的作用逐渐减弱；调差系数的作用逐渐增强；最大频率偏差和稳态频率偏差对于调差系数的灵敏度最大。由上述分析可知：惯性时间常数为惯量响应阶段的主导参数；改善等效惯性时间常数能够有效改善ROCOF；调差系数为一次调频阶段的主导参数，改善等效调差系数能够有效改善系统频率偏差。

2 储能系统的惯量支撑原理

储能系统的频率支撑能力不受自然因素的影响，具有响应快速、灵活可控和运行平稳的优势，尤其是大量可再生能源并入电网时，在电网中配置适量的储能，并提供一定的惯量支撑，能够提高可再生能源的消纳能力，满足电力系统的调频需求。储能向系统提供惯量支撑的方法从原理上可以分为电流源性虚拟惯量和电压源型虚拟惯量。

2.1 电流源型虚拟惯量控制基本原理

电流源型虚拟惯量控制基本思路是将系统的测量频率反馈至变流器有功控制环节以改变有功功率参考值，利用储能来满足系统的有功调节需求[19]。电流源型虚拟惯量控制本质上是一个功率源，并不增加系统等效惯量，也不具备同步机组在扰动初期的扰动功率分配能力，且频率测量过程导致其与同步机的瞬时自然响应存在约100 ms延时[20]。

虚拟惯量控制参与调频的有功功率为

2.2 电压源型虚拟惯量控制基本原理

电压源型虚拟惯量控制策略如图3所示。

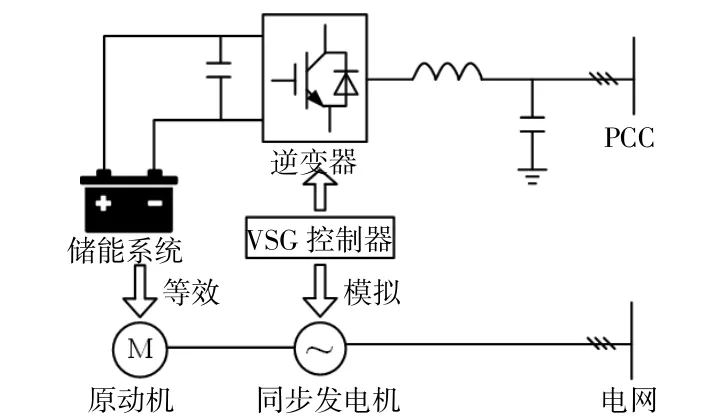
图3 电压源型虚拟惯量控制结构图Fig.3 Controlstructure diagram of voltagesourcevirtualinertia

电压源型虚拟惯量控制将同步发电机转子运动方程和电磁方程引入储能系统的逆变器控制，使并网运行的储能单元表现出和同步机相似的外特性，能够响应电网频率的变化而改变自身的功率输出，为电网提供必要的惯量支撑能力[21]。

VSG的运动方程可以等效为同步发电机的转子运动方程，其标幺值形式为

式中：Pm*为虚拟机械功率；Pe*为虚拟电磁功率，由VSG的输出功率等效；ω*为VSG的转子角频率；ωg*为电网实际角频率；ω0为额定角频率；δ为功角；Tj为虚拟同步机的惯性常数；D为阻尼系数。

对式（9）进行拉普拉斯变换，可得到VSG控制的小信号模型和有功功率的表达式：

当电网频率波动时，VSG有功输出随系统频率的变化量由储能系统提供，储能单元的出力由系统频率偏差和VSG的控制参数决定。

3 系统频率响应改进模型

实际电网的频率响应曲线一般由全状态时域仿真获得，但仿真速度较慢，且无法实现不同频率控制策略。SFR模型仿真速度快，能够实现不同的储能频率控制策略，但由于其基于系统频率均一的假设，用于频率响应分析时，不能反应区域间频率响应。

为研究不同储能频率控制策略对实际电网的频率支撑能力，本文将实际电网分为被研究区域内部、外部以及储能系统。对三者各自的频率响应分别建立模型并求取参数，以提高模型的精度。频率响应等值模型建立流程如图4所示。

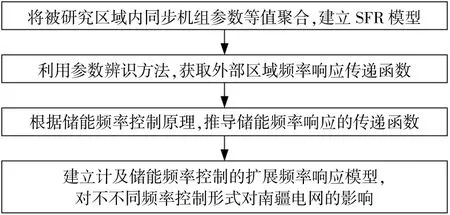
图4 频率响应模型建立流程图Fig.4 Theflowchart of establishing extended frequency response model

3.1 区域内同步机组等值模型及参数

目前，电力系统中常见的同步发电机组主要包括非再热式汽轮机、再热式汽轮机和水轮机，在频率响应模型中，主要考虑反应其有功功率调节特性的原动机和调速器模型[18]。

结合以上分析，建立考虑不同类型同步机组的频率响应模型，如图5所示。

图5 考虑不同类型同步机组的频率响应模型Fig.5 Frequency response model considered of different types of synchronous generators

3.2 基于参数辨识的区域外频率响应等值模型

SFR模型研究区域电网频率响应时，未考虑外部区域频率响应是SFR模型误差来源之一。区域内SFR模型参数相对容易获取，但外部区域对本区域的频率响应难以确知，因此本文提出一种基于参数辨识的外部区域等值方法以减小SFR模型误差。

设外部区域的频率响应传递函数为

利用粒子群算法[23]对传递函数中的参数进行辨识，流程如图6所示。

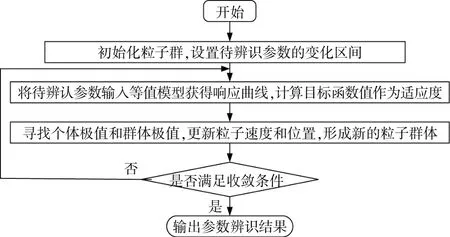
图6 粒子群算法参数辨识流程Fig.6 Parameters identification process of PSO

粒子群算法的适应度函数选择，频率响应模型输出Δfout与实际时域仿真输出Δfact之间误差平方和，即：

式中：θ为待辨识参数，θ=[a0，a1，b0，b1，b2]T；Δfout为等值模型输出的频率偏差；Δfcat为实际的频率偏差；k为第k个采样点。

3.3 计及储统惯量支撑的频率响应模型

设储能系统用于惯量支撑的有功出力为ΔPESS，储能环节的频率响应传递函数为

电流源型和电压源型虚拟惯量分别按照式（8），（12）作为储能系统的频率响应传递函数。当储能环节提供电流源型虚拟惯量时，系统的等效惯性时间常数不发生变化，当储能环节采用电压源型虚拟惯量控制时，由于其控制方式参与系统扰动功率分配，系统等效惯性时间常数增加，即：

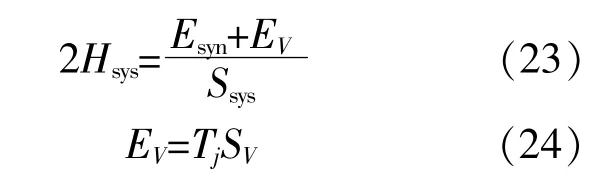
式中：Hsys为系统等效惯性时间常数；Esyn为同步机组动能；EV为VSG提供的动能；Ssys为系统总额定容量，包括常规机组和可再生能源机组；Tj为虚拟惯性时间常数；SV为储能单元所对应的VSG额定容量。

将被研究区域的内部、外部和储能系统的功率施加在等值转子上，获得计及储能系统惯量支撑的频率响应模型，用于研究不同频率控制策略对电网频率响应的影响，如图7所示。

图7 计及储能惯量支撑能力的频率响应模型Fig.7 Frequency response model considered inertia support capacity of energy storage

同步机组频率响应模块中，K为同步机组出力占比，将其作为同步机组频率响应的增益系数，能够反映不同可再生能源占比下的同步机组调频能力变化。外部频率响应等值模块中传递函数Gout（s）使用3.2节参数辨识结果。储能频率响应等值模块中，假设系统中存在n台同步机，m台虚拟同步机，则二者均具有扰动功率分担能力，在扰动初始时刻按照同步功率系数分担功率，因此能够增大系统等效惯性。ΔPGn，ΔPGm分别为同步机和虚拟同步机分担的有功功率大小；电流源型虚拟惯量控制不具备扰动分担能力，因此用与频率偏差相关的功率注入表示，等效减小系统的有功缺额。

4 算例分析

为验证系统频率响应改进模型的有效性，以及不同储能频率控制策略对实际电网的惯量支撑能力，本文以新疆南疆地区电网为算例建立仿真模型进行仿真验证。

4.1 南疆地区频率响应特性分析

采用的系统模型以新疆电网南疆地区网架为基础，建立南疆地区频率响应模型。电网网架结构如图8所示。

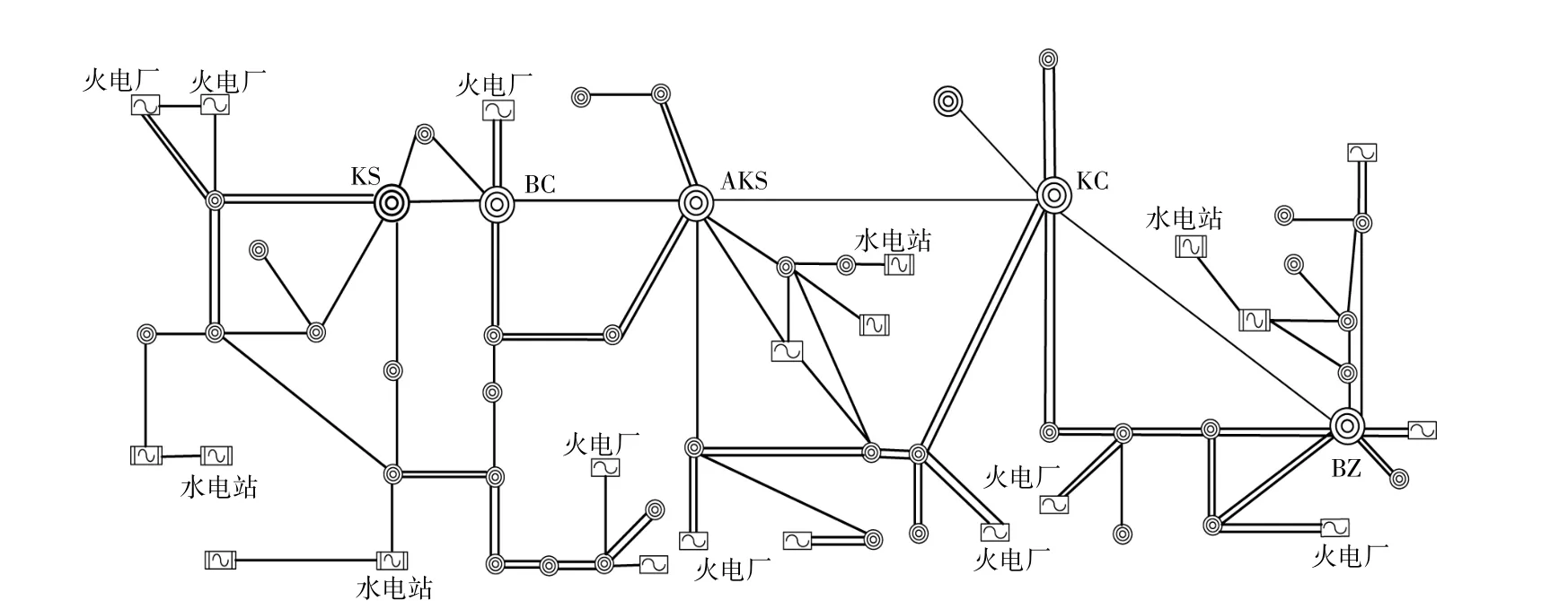
图8 南疆电网网架结构Fig.8 The grid structure of Southern Xinjiang power grid

考虑到南疆地区电网同步发电机组类型，将南疆地区内部的同步发电机等值聚合为1台再热式火电机组和1台水电机组，各类发电机的等值参数如表1所示。

表1 各类发电机等值参数Table 1 Equivalent parameters of various generators

对于南疆地区外部区域的频率响应等值模型，按照前文方法进行参数辨识，辨识结果如表2所示。

表2 外部区域辨识参数结果Table 2 Frequency response parameters identification results of external area

以南疆地区可再生能源增加9.0×106kW为算例，设置系统发生扰动功率为0.07 p.u.，将本文所建立的频率响应模型与PSASP时域仿真频率响应曲线对比，如图9所示。由图9可以看出，该可再生能源占比下，发生功率扰动后，南疆地区频率跌落迅速，ROCOF约为0.8 Hz/s，最大频率偏差约0.8 Hz，有触发防孤岛保护和低频减载的风险。通过仿真对比可以看出，本文所提出的频率响应模型得到的频率响应曲线与时域仿真结果较为接近，可用于实际电网频率响应分析与储能惯量支撑能力研究。

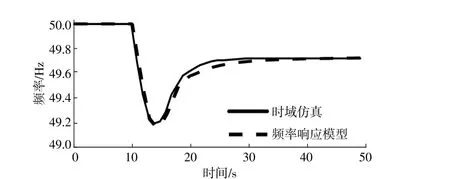
图9 频率响应模型与时域仿真的曲线对比Fig.9 Curve comparison of frequency response model and time domain simulation

4.2 储能惯量支撑对南疆电网的影响

为验证不同惯量支撑策略对电网频率响应的影响，本文按照3.3节所述方法，搭建计及不同储能系统惯量支撑控制的南疆电网频率响应模型。有功功率扰动大小设为0.07 p.u.，通过调整频率控制器参数，使得两种控制方式下储能系统向电网提供的最大有功功率相同，以此来对比电压源型和电流源型虚拟惯性控制的电网频率响应特性。本文将两种虚拟惯量形式下储能向系统提供的最大有功功率均设置为0.03 p.u.，并以此为约束条件确定频率控制器参数。在储能释放的最大有功功率相同的前提下，电压源型和电流源型虚拟惯性形式下的电网频率响应如图10所示。

由图10可以看出，由于电压源型虚拟惯量能够模拟同步机组的瞬时惯量响应，具有参与扰动功率分配能力。在相同的储能容量配置下，对ROCOF和最大频率偏差的改善性能均优于电流源型虚拟惯量，能够明显提升系统的ROCOF和最大频率偏差；由于电流源型的虚拟惯量响应存在延迟，无法模拟同步机的瞬时自然响应，因此其惯量支撑能力较差，对于最大频率偏差的改善效果不及电压源型虚拟惯量。

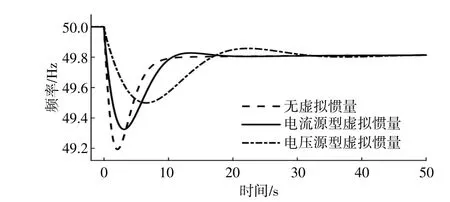
图10 不同储能惯量支撑方法对南疆电网的影响Fig.10 Influence of different energy storage inertia support methods on Southern Xinjiang power grid

图11为系统频率响应FFT分析结果。

图11 不同储能惯量支撑方法FFT分析结果Fig.11 FFT analysis results of different energy storage inertia support methods

由图11可以看出，电压源型虚拟惯量控制具有更少的低频分量，其控制效果优于电流源型虚拟惯量控制。

在储能配置充足的前提下，电流源型虚拟惯量能够通过参数设置达到与电压源型虚拟惯量相同的控制效果，但对储能有功功率的需求增大。本算例中，电流源型虚拟惯量控制要达到图10所示的电压源型虚拟惯量的效果，储能系统须向系统提供的最大有功功率达到0.06 p.u.。

5 结论

为应对大规模可再生能源接入电网系统所带来的频率稳定问题，本文基于灵敏度分析了不同频率响应阶段的主导参数，分析了不同储能惯量支撑方案的机理；提出了改进的频率响应模型，并在此基础上研究了不同储能惯量支撑方法对南疆电网频率的影响。结论如下：①根据轨迹灵敏度分析可知惯性时间常数是惯量响应阶段的主导参数，为应对南疆大规模光伏接入带来的频率稳定问题，利用储能提供虚拟惯量是提高系统频率稳定性的有效措施；②本文提出的改进频率响应模型能够较为准确地描述实际电网的频率响应，便于实现不同储能频率控制策略，能够用于研究频率控制策略对实际电网频率响应的影响；③储能系统容量配置相同的前提下，电压源型虚拟惯量控制方法相比于电流源型虚拟惯量控制方法具有更好的惯量支撑能力。