Determination of neutron-skin thickness using configurational information entropy

Chun-Wang Ma • Yi-Pu Liu • Hui-Ling Wei • Jie Pu • Kai-Xuan Cheng • Yu-Ting Wang

Abstract Configurational information entropy (CIE) theory was employed to determine the neutron-skin thickness of neutron-rich calcium isotopes.The nuclear density distributions and fragment cross sections in 350 MeV/u 40-60Ca+9Be projectile fragmentation reactions were calculated using a modified statistical abrasion-ablation model.CIE quantities were determined from the nuclear density,isotopic,mass,and charge distributions.The linear correlations between the CIE determined using the isotopic,mass,and charge distributions and the neutron-skin thickness of the projectile nucleus show that CIE provides new methods to extract the neutron-skin thickness of neutron-rich nuclei.

Keywords Neutron-skin thickness · Configurational information entropy·Cross section distribution·Projectile fragmentation

1 Introduction

Next generation radioactive nuclear beam facilities will provide new opportunities to explore extreme nuclei near and beyond drip lines.Nuclei with a large neutron excess can form exotic neutron-skin or halo structures,which have attracted significant interest experimentally and theoretically for the past 30 years.The neutron-skin thickness is defined asδnp=δn-δp,which denotes the difference between the point neutron and point proton root-meansquare(RMS)radii of a nucleus.Many methods have been developed to experimentally determine the neutron-skin thickness.However,most of the models are indirect measurements and model dependent.Typical methods used to determine neutron-skin thickness include the reaction cross section (σR),charge-changing cross section (σcc) [1,2],electric dipole polarizability [3],photon multiplicity [4],theπ-/π+ratio or Σ-/Σ+[5,6],3H/3He ratio [7],andαdecay half-life time [8].The projectile fragmentation reaction,which is the main experimental approach for studying rare isotopes,is suitable for determining the neutron-skin thickness owing to the obvious experimental phenomena induced by the neutron-skin structure [9,10].For example,isospin effects in the isotopic cross section[11],neutron-abrasion cross section (σnabr) [12],neutron removal cross section [13],mirror nuclei ratio or isobaric ratio [14],and isoscaling parameter (α) [15].Parity-violating electron scattering (PVS) is the only method used to determine neutron-skin thickness that is modelindependent.Ref.[16] reports a theoretical investigate of PVS for48Ca and208Pb,and a theoretical investigation of Bayesian approach is given in Ref.[17].Determining the neutron-skin thickness of48Ca and208Pb is presently of significant interest and is listed in the U.S.2015 Long Range Plan for Nuclear Science [18].The lead radius experiment(PREX)has been previously used to determine the neutron-skin thickness of208Pb [19].A recent PREX result indicates a much thicker neutron skin than previously predicted [20].Determining the neutron-skin thickness of nuclei near the neutron drip line remains an important research outcome and is one of the most interesting topics in the new era of radioactive beam facilities.

Information entropy theory was established by C.E.Shannon [21].The theory makes it possible to transform variables in a system into an exact information quantity[22]and has been used in various applications[23,24].The first application of information entropy theory in heavy-ion reactions can be traced to the study of nuclear liquid-gas transition in nuclear multifragmentation [25].Recent studies have extended it to study the information entropy carried by a single fragment produced in projectile fragmentation reactions,and revealed the scaling phenomenon of fragments covering a wide range of neutron excess[26-28].Configurational information entropy (CIE) was developed to quantify the information entropy of a physical distribution [29],which connects the dynamical and informational contents of a physical system with localized configurations.Many applications of CIE methods can be found in Korteweg-de Vries (KdV) solutions,compact astrophysical systems,and scalar glueballs (see a brief introduction in Ref.[23]),theoretical research of new Higgs boson decay channels [30],deploying heavier eta meson states in AdS/QCD [31],confinement/deconfinement transition in QCD[32],quarkonium in a finite density plasma [33],time evolution in physical systems [34,35],etc.In projectile fragmentation reactions,fragment distributions show a sensitive dependence on the change in neutron density [36-38],which makes it possible to determine the neutron-skin thickness of neutron-rich nuclei.In this study,the CIE method was adopted to quantify the CIE of nuclear density and fragment distributions in projectile fragmentation reactions.The analyzed data were generated using a modified statistical abrasion ablation(SAA)model,which is known to be a good model for describing the fragment cross sections of projectile fragmentation reactions [39,40].

2 Theories

2.1 Modified statistical abrasion-ablation model

The modified statistical abrasion-ablation (SAA) model[39,40] can be used for projectile fragmentation reactions at both intermediate and high energies,which improves the original SAA model by Brohm and Schmidt[41].In quasifree nucleon-nucleon collisions,the reaction is described as a two-step process:In the initial stage,the nucleons are described by a Glauber-type model as ‘‘participants’’ and‘‘spectators’’,where the participants interact strongly in an overlapping region between the projectile and target,while the spectators move virtually undisturbed [42].In the second stage,the excitation energy is compared to the separation energies of protons,neutrons,andαto determine the type of particle the prefragment can emit according to min(sp，sn，sα).After the de-excitation calculation,the cross sections of final fragments that are comparable to the measured fragments were obtained.The description of the modified SAA model is presented in Refs.[23,39,40].The colliding nuclei are composed of many parallel tubes oriented along the beam direction.Their transverse motion is neglected,and the interactions between the tube pairs are independent.For a specific pair of interacting tubes,the absorption of the projectile neutrons and protons is assumed to be in a binomial distribution.At a given impact parameter b,the transmission probabilities of neutrons (protons) of an infinitesimal tube in the projectile are calculated using

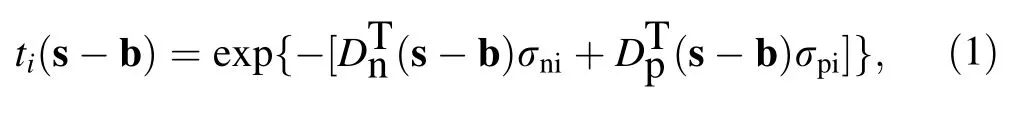
whereDT is the normalized integrated nuclear density distribution of the target along the beam direction for protons∫d2sDTp=ZT and neutrons∫d2sDTn=NT (NT andZT are the neutron and proton numbers of the target,respectively).s and b are defined in a plane perpendicular to the beam direction,andσi′idenotes the free-space nucleon-nucleon cross sections (i′，i=n for neutrons andi′，i=p for protons) [44].The average absorbed mass in the infinitesimal tube limit at a given b is

For a specific fragment,the production cross section can be calculated using

whereP（ΔN，b）andP（ΔZ，b）are the probability distributions of the abraded neutrons and protons at a given impact parameterb,respectively.σ（ΔN，ΔZ）is the residual fragment after the abrasion stage,which is called the prefragment.The excitation energy of the prefragment is calculated asE*=13·3〈ΔA（b）〉 MeV,where 〈ΔA（b）〉 is the number of abraded nucleons from the projectile,and 13.3 MeV is the mean excitation energy owing to an abraded nucleon [43].In the second stage,the excitation energy is compared to the separation energies of protons,neutrons,andαto determine the type of particle the prefragment can emit according to min(sp，sn，sα).After the de-excitation calculation,the cross sections of final fragments that were comparable to the measured fragments were obtained.

Fermi-type density distributions were adopted for protons and neutrons in a nucleus,as shown in the equation below:

whereis the normalization constant of neutrons (i=n)or protons(i=p),tiis the diffuseness parameter,andCiis half the density radius of the neutron or proton density distribution.

2.2 Configurational information entropy method

To determine the quantity of CIE incorporated in the fragment distributions,definitions of CIE were introduced.For a system with spatially localized clusters,when performing the CIE analysis,a set of functionsf（x）∈L2（R）and their Fourier transformsF(k) obey Plancherel’s theorem [45]:

wheref(x) is square-integrable-bounded.The model fractionf(k) is defined as:

where the integration is over allk,F(k)is defined,anddis the number of spatial dimensions.

The model fractionf(k)measures the relative weight of a given modek.The quantity of CIESC［f］ is defined as a summation of the Shannon information entropy off(k)[21]:

Thus,the quantity of CIE has information about configurations compatible with certain constraints of a given physical system.If all the modeskhave the same mass,thenfm=1/N.The discrete configuration entropy reaches a maximum atSC=lnN.If there is only one mode,SC=0.

Continuous CIE can also be defined for continuous distributions,such as the nuclear density distribution.For non-periodic functions in the interval (a,b),

3 Results and discussion

The 350 MeV/uApCa+9Be reactions were calculated using the modified SAA model (Ap refers to even mass numbers from 40 to 60).The cross sections of fragments withZranging from 3 to 20 were obtained.For the sake of clarity,only part of the calculated results are shown in the figures.Figure 1 is a plot of the Fermi-type nuclear density distributions and their fast Fourier transformation (FFT)spectra.An obvious increase inρn is observed from40Ca to60Ca,whereas the opposite trend is observed forρp.A two-peak structure is evident in the FFT spectra,where the second peak is lower than the first.The difference between the neutron and proton density distributions Δρ=ρn-ρp is also shown.For40Ca,Δρis very small,while Δρincreases as the neutrons in the projectile increase.The peaks in the FFT spectra ofρn andρp are not clearly shown.Based on the FFT spectraf(k),the CIE ofρn,ρp,and Δρcan be determined using Eq.(7),which are denoted by,respectively.

Fig.1 (Color online) Fermi-type nuclear density distributions [in panels (aj)] and the corresponding FFT spectrum [in panels (bj)].Panels (a1),(a2),and (a3) show the proton densities (ρp),neutron densities (ρn),and the nuclear density difference Δρ=ρn-ρp for 40-60Ca isotopes

The isotopic cross section(σZ)distributions produced in the 350 MeV/uApCa+9Be reactions are plotted in Fig.2.In panels(ai),fromZfr=7 to 20,the isotopic cross section distributions in the40-60Ca reactions are similar for fragments with smallZfr,while a shift to the neutron-rich side is observed for largerZfr.The symmetric Guassian-like shape of the isotopic distribution is altered by the enhanced cross sections of neutron-rich fragments in neutron-rich reaction systems,showing the isospin effect in fragment production induced by the increased neutron density on the surface of neutron-rich nuclei[40].The FFT spectra of the isotopic distributions are shown in Fig.2(bj).In each FFT spectrum,only one peak is observed.The amplitudes of the FFT spectra of different isotopic distributions decrease as the projectile becomes more neutron-rich,except forZ=20.Based on the FFT spectra ofσZdistributions,the quantities of CIE of the isotopic distributions are determined according to Eq.(7),which is denoted bySσZC［f］.

Fig.2 (Color online) The isotopic cross section distributions of fragments in the 350 MeV/u ApCa+9Be reactions calculated using the modified SAA model.Panels(aj)correspond to Z=7,12,16,and 20 isotopes,respectively,and panels (bj) plot the corresponding FFT spectra of (ai)

The correlation between theSC［f］ of the density distribution andδnp of the projectile nucleus is shown in Fig.3(a).Bothanddecrease linearly with an increase inδnp from40Ca to60Ca.also decreases linearly with increasingδnp,except for40Ca.The correlation between theof differentZfr andδnp of the projectile nuclei are plotted in panel (b).Theof isotopes fromZfr=10 to 18 are also found to decrease with the increasingδnp of the projectile nucleus.Theof the fragment near the projectile nucleus was more sensitive to the change inδnp.

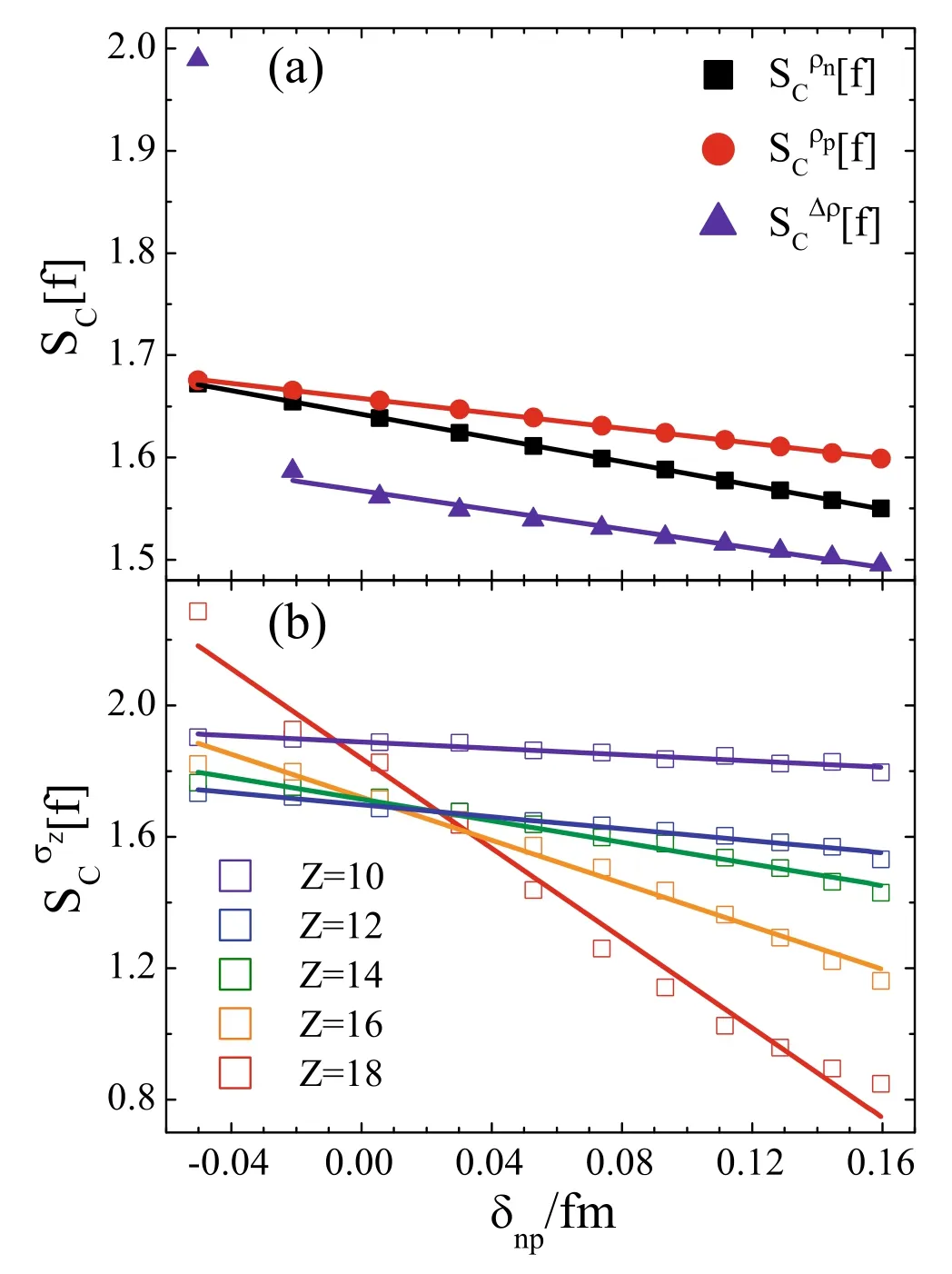
Fig.3 (Color online) a The correlation between the CIE of ρn(squares), ρp (circles),Δρ (triangles) and neutron-skin thickness δnp of ApCa. b Correlation between the CIE of the isotopic cross section distributions SσZC［f］and δnp of ApCa.The lines denote the linear fitting of the correlations

The mass yield(σA)distributions in the 350AMeVApCa+9Be reactions are shown in Fig.4.In each reaction,the mass yield increases with theAfr of the fragment until it is close to the projectile nucleus.In different reactions,a very similar trend of mass distribution was observed,which decreased with the increasing mass number of the projectile nucleus.The corresponding quantities of CIE were determined fromσAdistributions,which are labeled as.The correlation betweenandδnp for projectile nuclei is shown in Fig.4(b).Except for the bend point formed atδnp for42Ca owing to the transition of proton-skin to neutron skin,the～δnp correlation was found to be linear for reactions ofAp ≥44.

Fig.4 (Color online) Panel (a):The mass yield distributions of the 350 MeV/u ApCa+9Be reactions calculated using the modified SAA model.Panel(b):The correlation between ［f］determined from the mass yield distribution and the δnp of ApCa (Ap denotes even mass numbers from 40 to 60)

The charge cross section is defined as the summation of the isotopic cross sectionsσC=∑o σ（Ao，Z）.The charge cross section distributions in the 350AMeVApCa+9Be reactions are shown in Fig.5.Similar trends ofσC distribution trends similar to those ofσAwere observed.The determined CIE ofσC distributions,labeled as,were linearly correlated to the neutron-skin thickness of the projectile nuclei.

Fig.5 (Color online)Similar to Fig.4 but for the charge cross section distributions

The CIE approach transfers the experimental distributions to quantified parameters and provides information probes for determining the properties of a system.From the～δnp,and～δnp correlations,it was observed that the CIE determined from isotopic,mass,and charge distributions decrease with increasing neutronskin thickness,respectively,and they had good linear correlations.The determination of neutron-skin thickness,in particular,nuclei near the neutron drip line is limited by the unavailability of effective probes.The linear correlation between the CIE and neutron-skin thickness of neutron-rich nuclei provides new approaches to determine the neutron-skin thickness of the projectile nucleus by measuring the fragment distributions in projectile fragmentation reactions.

4 Summary

With the vast opportunities for very asymmetric nuclei available in the new era of radioactive ion beam facilities,neutron-skin thickness is one of the most important questions in nuclear physics.In this study,CIE theory is adopted to quantify the information entropy incorporated in nuclear density distributions and fragment cross section distributions in 350 MeV/u40-60Ca+9Be projectile fragmentation reactions calculated using the modified SAA model.CIE quantities of nuclear density distributionsisotopic cross section distributionsmass cross section distributionsand charge cross section distributionswere determined.The correlations between,andand～δnp were also investigated.For neutron-rich calcium projectiles,obvious linear dependences of,,andonδnp were observed.Theof fragments with differentZfr is shown to linearly depend on theδnp of the projectile nucleus.It is found that,if the isotopic distribution is sensitive to isospin effects in the projectiles,the extractedwill also be sensitive to theirδnp.Good linear correlations between,andδnp of the projectile nucleus were also observed.It is suggested that,from the viewpoint of CIE,the isotopic/mass/charge distributions in the projectile fragmentation reaction may be good probes for determining the neutron-skin thickness of neutron-rich nuclei.

In this work,the simple description of the nuclear density of a projectile nucleus is difficult to deal with nuclei of magic numbers,as well as large shape distortion.Further improvements should concentrate on the inputs of nuclear densities,such as the results obtained from density functional theories,relativistic mean and field theories,to better investigate the effects of nuclear density on fragment cross section distributions and related CIE quantities.

Author contributionsAll authors contributed to the study conception and design.Material preparation,data collection and analysis were performed by Yi-Pu Liu,Hui-Ling Wei and Chun-Wang Ma.The first draft of the manuscript was written by Yi-Pu Liu and Chun-Wang Ma and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.