基于小波分解的ABC-MGRU城市供水量预测模型

李唯特，陈 宇，于忠清

（青岛大学计算机科学技术学院，山东青岛266071）

0 引言

为了实现城市供水行业的规范管理以及高效运行，智慧供水应运而生。智慧供水的基础是对供水量的准确预测。城市供水量的短期预测，目的是了解未来的供水管网状况，从而进一步指导各种实际的决策，如供水调度，压力设定，以及管网漏损等。实现准确的供水量预测不仅可以满足城市的用水需求，还可以降低供水的成本。然而，影响城市供水量的因素很多，具有不确定性和强随机性，其数据是非线性且非平稳的时间序列，因此，对于城市供水量的准确预测不是一件容易的事。

近年来，对于供水量预测，国内外学者进行了大量的相关研究，主要有传统预测方法（回归分析，ARIMA）和新型预测方法（人工神经网络，组合模型）等［1］。张倩等［2］建立了基于灰色预测模型和线性回归预测的需水量组合模型，将单个模型与建立的组合模型进行了对比，组合预测模型的误差小很多。Murat等人［3］提出的利用ARIMA 构建时间序列模型预测城市水的需求和供应也得到了较好的效果，但其忽略了外部变量的影响。顾熹等人［4］提出了一种结合多变量相空间重构和高斯过程回归的短期负荷预测方法，该方法没有考虑到负荷序列的多尺度特征。王亮等人［5］提出了一种基于粒子群优化的城市日用水量预测方法，优化后的BP 神经网络运算速度，泛化能力以及预测精度都得到了一定的提高。Salvatore 等人［6］在不考虑其他影响因素的情况下使用不同的小波基结合人工神经网络去预测未来几个月的用水量，结果表明通过小波分解可以提高预测精度。

为了获得高精度和高效率的城市供水量预测模型，本文提出了一种基于小波分解结合人工蜂群算法优化的多变量门控循环单元（WD-ABC-MGRU）模型来预测城市日供水量。该方法综合了上述研究方法的优点，克服了单一方法的缺点和局限性，不仅考虑了供水量序列数据的不平稳性，利用小波分解充分挖掘多尺度序列特征，还考虑了供水量强相关影响因素并进行相空间重构，并且用人工蜂群优化算法对模型的超参数进行了优化，使预测更加精准。通过对某市供水量进行分析预测，实验结果表明该方法用于城市日供水量预测的有效性，具有较好的实用价值。

1 相关方法理论基础

1.1 小波分解与重构

小波变换可以将非平稳时间序列分解成具有不同频域的多个子序列，小波分解与重构是其核心。Mallat［7］提出了一种易于实现且计算较少的多尺度分析算法。时间序列X={xi|i=1，2，…，k}的离散小波变换函数为

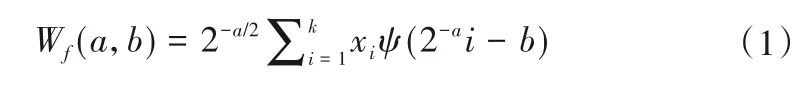
式中：a和b分别决定小波伸缩和平移的幅度；Wf是特定子序列的小波系数；ψ是小波基函数。

在式（1）中，Wf应用下采样，以使用低通滤波器LP(ψ(i))获得第n层的近似（低频）系数cAi，并使用高通滤波器HP(ψ(i))）获得n层的细节（高频）系数cDi。原始信号的计算如式（2），其中i= 1，2，…，n。

城市供水量数据有着非平稳且随机性强的特点，利用小波分解和重构可以将其处理为多层较为平稳的低频分量和高频分量，从而能够更好地分析供水量数据。3 层小波分解及重构其过程见图1。

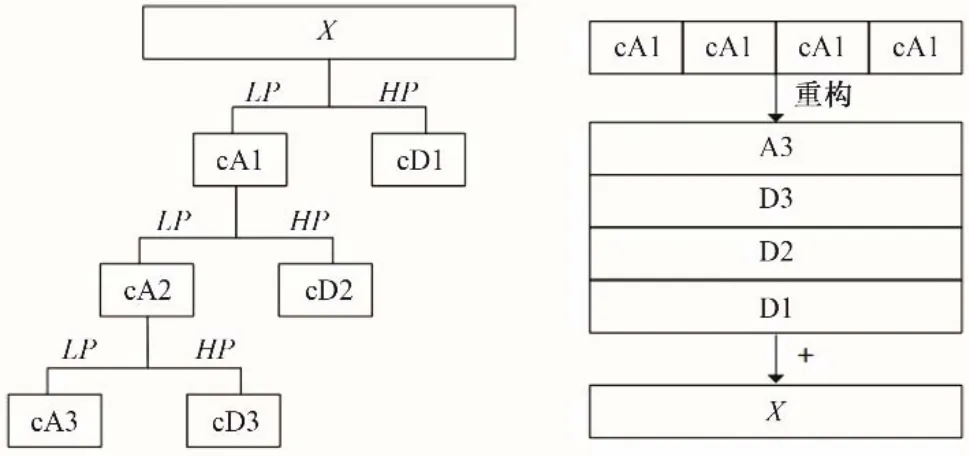
图1 小波分解（左）与重构（右）示意图Fig.1 Schematic diagram of wavelet decomposition（left）and reconstruction（right）

通过小波分解对时间序列在不同尺度上进行分解，从而将原始时间序列X 分解成为低频系数cAi和高频系数cDi两部分。然后通过系数重构从低频系数中得到与原始时间序列的低频分量Ai，从高频系数中得到原始时间序列的高频分量Di，重构系数后的每个分量长度与原始时间序列长度相同，对分量进行相应处理后进行直接求和得到新的序列X，计算方法如式（3），这种方法可以提高原始时间序列数据的预测精度［8］。

1.2 人工蜂群算法ABC

ABC 算法是一种模拟蜜蜂觅食行为的优化算法，属于较为简单且灵活的一种群优化算法，由Karaboga［9］于2005年提出。ABC 算法是解决复杂非线性优化问题的有效方法，有研究证明在寻找多变量函数最值方面优于遗传算法、粒子群优化算法和其他一些群优化算法。该算法包括三种蜜蜂，第一种是雇佣蜂，与蜜源相对应并在蜜源领域内搜索。第二种是观察蜂，通过观察雇佣蜂的舞蹈来选择蜜源。第三种是侦查蜂，如果蜜源多次更新没有改进，则放弃该蜜源，雇佣蜂转为侦查蜂随机寻找新蜜源，其流程图见图2。

图2 人工蜂群算法流程图Fig.2 Artificial bee colony algorithm flow chart

ABC算法蜜源位置（问题初始解）可以定义为式（4）。

其中i= 1，…，N，j= 1，…，D。参数N和D分别为蜜源数量和变量数量。式（5）表示算法在xk区域中生成的新解vjk。

其中φjk和xjk代表随机数的均匀分布和第k个参数的解集中的第j个解。在这些条件下，如果新的解适应度更强，它将取代之前的解。随后，侦查蜂使用式（6）为每个蜜蜂选择一个解决方案以及计算可能性，将从这些解中选出最合适的结果。

1.3 门控循环单元

门控循环单元（GRU）具有循环神经网络的门控机制，由Kyunghyun Cho［10］等人于2014年提出。GRU 是长短期记忆（LSTM）神经网络的变体，和LSTM 一样，GRU 也主要用于解决典型神经网络中的“梯度消失”问题，从而改进网络中长期依赖关系的学习。

GRU 层没有独立的存储单元，也没有单独的遗忘门。由于GRU 的参数比LSTM 的少，设计更简单，因此GRU 是一个更轻量级的模型，训练更快，GRU 在某些较小且频率较低的数据集上表现出更好的性能［11］。其典型的GRU单元图见图3。

图3 GRU基本结构Fig.3 Basic structure of GRU

根据式（7）和（8），rt和zt分别为重置门和更新门，激活函数σ将值压缩到［0，1］，从而获得门控信号。对于式（9）表示当前时刻的候选状态，由重置门rt决定，而对于式（10），ht为当前隐藏状态，根据更新门对上一时刻隐藏状态ht-1和当前候选状态来确定当前隐藏状态ht。更新公式同时进行了遗忘和记忆两个步骤，门控信号z的范围为［0，1］。z越接近1，代表记忆下来的数据越多；而越接近0 则代表遗忘得越多。这一步操作就是忘记ht-1中的某些信息，并加入当前时刻的某些信息。

1.4 WD-ABC-MGRU模型

以相关影响因素为输入的BP 神经网络无法考虑时序变化规律，以单变量为输入的时间序列模型效果较好，而将多种相关影响因素与时间依赖关系结合可以得到更好的模型［12］。供水量不仅受多种外部影响因素，其自身有一定的周期性，而且还存在着多尺度时序特征。针对多尺度时序特征，采用小波分解和系数重构可以增加对时序数据细节信息的利用，提高预测精度［13］。

考虑到受多种外部因素影响，采用多变量GRU 模型（MGRU）。MGRU 模型的一些超参数可以影响模型的收敛速度和效果，比如隐藏层的神经元个数、dropout、epochs 和batch_size等。这些参数可以通过ABC 算法来进行优化，优化后得到的参数来获得最优的模型以获得精确的预测结果。因此，本文提出了以一种基于小波分解的人工蜂群优化多变量门控循环单元模型，即WD-ABC-MGRU 模型。

WD-ABC-MGRU 模型流程图见图4，其具体步骤如下：

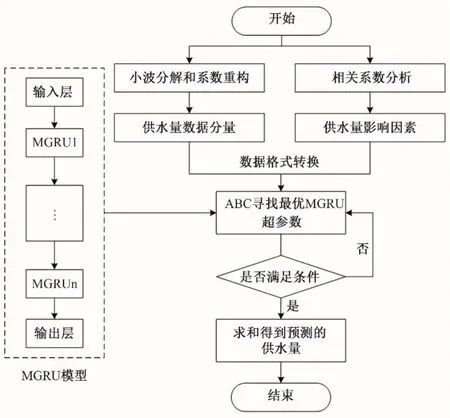
图4 WD-ABC-MGRU模型流程图Fig.4 WD-ABC-MGRU model flow chart

步骤1：首先对日供水量数据进行小波分解，然后对其系数重构，得到供水量数据分量；

步骤2：将供水量数据分量与其影响因素数据进行结合并根据相空间重构做数据格式转换处理，加载训练集；

步骤3：初始化蜂群算法参数，确定所需要优化的MGRU 超参数并给出搜索范围，然后在范围内随机产生初始解（蜜源，也就是超参数组合）；

步骤4：用初始解进行MGRU 模型训练，然后用训练集和验证集的均方根误差RMSE 平均值［14］评估每个初始解的适应度（寻找最小适应度），计算公式如下：

式中：m，n分别为训练集和验证集样本数；ytrain，分别为训练集真实值和预测值；yval，分别为验证集真实值和预测值；

步骤5：对于每一个雇佣蜂在邻域搜索产生新的解并计算适应度，用贪婪算法：如果新的解优于先前的解则改变，否则保留不变；

步骤6：计算蜜源的概率；

步骤7：对于每个观察蜂按照概率选择解，然后进行搜索产生新解并计算适应度，用贪婪算法：如果新的解优于先前的解则改变，否则保留不变；

步骤8：判断是否有需要放弃的解，若有，则用侦查蜂产生的新解来替换；

步骤9：记录当前最优解（最小RMSE所对应的MGRU 超参数组合）；

步骤10：判断是否满足循环终止条件，若满足，循环结束，否则返回步骤4继续搜索；

步骤11：将各分量的预测结果求和得到最终预测的日供水量。

2 数据预处理

2.1 缺失值与异常值处理

本文数据来自某市2017年11月至2019年12月近两年的日供水量数据，对于个别缺失数据采用均值、中位数和众数等进行填补。

根据3σ准则，数值分布在(μ- 3σ，μ+ 3σ)中的概率为0.997 3，超出这个区间范围的数据为异常值，应对其进行处理。本文对于供水量数据中异常数据采用3σ准则进行检测，然后采用和个别缺失数据同样的方法进行填补。最终的日供水量序列数据见图5。

图5 处理后的日供水量序列Fig.5 Daily water supply sequence after treatment

2.2 城市日供水量气象因素分析

对于供水量预测有很多气象影响因素，所获取的气象数据包括气温，降水量，风速，日照时数，相对湿度，气压等特征。供水量大小也存在节假日效应，因此供水量分析考虑是否节假日这一影响因素是有必要的。对每个样本所属日期判定是否为节假日，工作日设为0，周末为1，法定节假日为2。

皮尔逊相关系数是在［-1，1］范围内的两个变量之间线性相关性的度量。其公式如下：r 值为正数表示正相关，为负数表示负相关，越接近1或-1表示线性相关性越强，而0表示没有线性关系。

本文采用皮尔逊相关系数评估选取相关性大的特征用于进行预测。具体结果见图6，最终选取最低气温，最高气温和平均气温以及节假日作为主要特征。由于上述数据的特征之间量纲不同，会影响分析的结果，为了消除量纲影响，对其进行归一化处理，处理后各数据特征处于同一量级，可以提升模型的收敛速度和精度。

图6 供水量影响因素相关系数分析Fig.6 Correlation coefficient analysis of influencing factors of water supply

2.3 小波分解与系数重构

小波分解需要先确定小波基函数和分解尺度，由于各个小波基函数性能不同，且其分解尺度不同，对于复杂的供水量序列选取到最佳的小波基函数和分解尺度是非常重要的。

为了降低重构误差对所提出方法的影响，本文选取几种常见的小波基函数和不同的分解尺度，分别计算其重构误差。最终得到最佳分解效果（最小重构误差）所对应的小波基函数为db2，分解层数为3。见图7（a），为分解后得到的1 个低频（近似）分量和3个高频（细节）分量。对这些分量进行系数重构［见图7（b）］，然后将其直接加和就可以得到小波分解和重构后的供水序列。

图7 日供水量数据经过小波分解和系数重构Fig.7 Daily water supply data undergoes wavelet decomposition and coefficient reconstruction

2.4 相空间重构

多变量供水量序列存在混沌特性，可以通过相空间重构从数据中提取原有动力学特性，减少信息丢失。本文通过C-C 方法对多变量供水量序列数据重构相空间，得到嵌入维数n为7，延迟时间τ为1。对于不同的模型，其输入数据格式不同，需要将全市日供水量数据和上述分析所选取的影响因素进行数据格式转换，将数据集转化为监督学习数据集，处理后的格式见表1。

表1 数据格式转换Tab.1 Data format conversion

表1 中将其格式转换后的数据按照6∶2∶2 划分为训练集，验证集，测试集。

3 实验结果与分析

经过多次实验结果对比分析，MGRU 模型考虑了多变量的影响因素，效果比GRU 模型效果好，而WD-MGRU 不仅考虑了多变量因素并进行相空间重构，又考虑了供水量数据中的多尺度序列结构特征，其效果优于MGRU。过程中发现WD-MGRU层数为3 时结果较好，故MGRU 层数设置为3，然后通过1.4 中所介绍的WD-ABC-MGRU 算法模型对其超参数进行优化，具体结果见表2，其中unitsi为第i个MGRU 层的神经元个数，batch_size为一次训练的样本数，epochs为数据集参与训练的次数，dropout为单元的丢弃比例，lr为学习率。

表2 WD-ABC-MGRU模型超参数搜索范围和结果Tab.2 WD-ABC-MGRU model hyperparameter search range and results

为了验证该模型对城市供水量预测的优势性，使用上表中优化后的超参数对相空间重构后的各供水量分量（A3，D1，D2，D3）进行预测，其结果加和得到预测的供水量。将最终的WDABC-MGRU 模型与GRU，MGRU，WD-MGRU，WD-ABC-BP 模型结果进行对比评估，其测试集对应的真实值和预测值对比见图8。

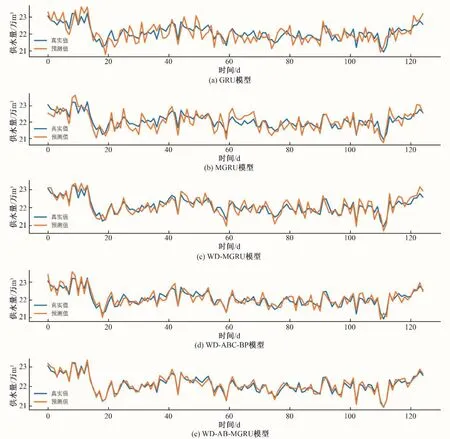
图8 5种模型真实值和预测值对比Fig.8 Comparison of the true and predicted values of the five models

以上5种模型的模型评估结果见表3。

表3 五种模型评估指标对比Tab.3 Comparison of evaluation indicators of four models

通过以上分析，WD-ABC-MGRU 模型预测结果的各项评估指标都优于其他模型，其RMSE和MAPE仅为GRU 的30%左右，R2达到0.87，供水量数据的拟合程度最优，预测效果最好。

GRU 模型虽然可以解决梯度消失和梯度爆炸的问题，由于只考虑了供水量时间序列，没能考虑其他相关影响因素对供水量的影响，所以预测值与真实值相差较大。而对于MGRU 考虑了多种相关影响因素，采用多变量时间序列降低了一定的误差。WD-MGRU 因为对供水量序列进行了多尺度分解，充分挖掘了供水量序列的不同尺度的特征，误差得到了进一步的降低。WD-ABC-BP 虽然考虑了多尺度分解并进行参数寻优，但是没有考虑供水量数据存在的时序特征。WD-ABC-MGRU 模型结合了以上模型的优点，不仅解决了神经网络中出现的梯度消失和梯度爆炸的问题，还考虑了其他多种相关影响因素的时间序列，再加上用ABC优化算法对WD-MGRU 中的MGRU超参数进行寻优，得到了更好预测效果的模型，且有较高的可靠性。

4 结论

本文提出了基于小波分解的人工蜂群优化多变量门控循环单元模型（WD-ABC-MGRU），对日供水量进行模拟预测实验。首先采用皮尔逊相关系数进行分析，确定了与日供水量有较强相关性的影响因素。然后使用db2小波对日供水量进行分解与重构，其分解尺度为3 时，重构误差最小，保证实验的有效性的前提下，挖掘出了日供水量不同尺度的特征。将小波分解后的日供水量分量与其他影响因素结合并进行相空间重构，作为MGRU 的输入，再用ABC 优化算法对MGRU 的超参数进行寻优，得到更好预测效果的模型。WD-ABC-MGRU 结合了多尺度多变量和自动化调参的优点，结果表明其模型预测效果比GRU，MGRU，WD-MGRU，WD-ABC-BP 更好，对日供水量预测精度更高，可以更好地对水厂决策进行指导。然而实验仅用了一个地方的供水量数据，研究结论是否通用仍需大量实验验证。因此，在以后的研究中，还需要应用于更多场景，以验证方法的通用性。□