现金周转期异象：来自中国A股的证据

王鹿鸣

（东北财经大学 金融学院，辽宁 大连 116025）

一、引 言

现金周转期（CCC），也称现金周期、现金循环周期，指从公司付出现金购买原材料到卖出产品收到现金之间的时间跨度，其表示一个公司的现金在其经营活动中占用的天数。大多数情况下，原材料采购和商品销售都是赊账形式的，这种商业惯例使得存货和应收账款产生了一个占用资金的时间。无论从融资成本还是机会成本的角度，这一时间都会造成相当大的财务负担，所以公司会尽可能缩短现金周转期，以提高资金周转率，避免这种成本负担。现金周转期最早在1980年由Richard和Laughlin提出，用作公司流动性分析中的一个动态指标。正如Cagle等所指出，现金周转期是一种包含时间的度量指标，它弥补了使用静态流动性度量，诸如流动比率的许多缺点。因此，分析师和投资者认为现金周转期用于财务分析是更为有效的，它已经成为近年来越来越重要的财务指标。理论上，现金周转期越小，显示公司的资金周转率越高，意味着公司的管理效率越高、盈利能力越强，因而其股票定价应该越高。

研究现金周转期对资产定价影响的文献较少。对现金周转期的关注主要集中在该指标对公司盈利能力的影响。Shin和Soenen使用1975—1994年的58 985个公司样本，发现现金周转期的长度与公司盈利能力之间存在很强的负相关关系，Raddatz、Tong和Wei认为拥有较高现金周转期的公司必须等待更长的时间才能从销售中获得现金，因此将现金周转期作为衡量营运资金依赖外部融资水平的一个指标。He和Xiong认为高现金周转期的公司容易出现资金流动性下降的问题，在债务到期时，更有可能承受展期风险并遭受重大损失，因而投资者对现金周转期非常敏感。国内对现金周转期的研究也大多集中在这一方面，汪平和闫甜以1995—2004年沪深两市所有A股上市公司作为研究对象，发现现金周转期与公司的资产报酬率呈负相关关系。袁卫秋、唐媚媚分别考察了制造业上市公司和机械设备行业上市公司，发现面临融资约束的上市公司，其营运资本管理效率指标即现金周转期，与盈利能力之间呈显著负相关关系，可以通过缩短现金周转期为公司释放更多的流动性，改善公司的盈利能力。也有研究认为现金周转期并非越低越好，帅亮针对新三板上市公司的研究发现现金周转期存在一个最优水平使得公司盈利能力最大化，即现金周转期与公司盈利能力之间存在“倒U型”关系。

一些研究调查了现金周转期的组成部分，如存货、存货周转期如何影响资产定价。Belo 和Lin将存货作为生产要素进行建模，认为存货增长与其股票预期收益呈反比。在实证方面，Thomas和Zhang、Belo和Lin证实了库存增加会对收益产生负面影响。另一些研究主要关注的是指标的估值效应。Alan等研究了库存周转期如何预测未来的股票收益，发现存货周转期与未来股票收益之间存在非单调关系。Wang研究了现金周转期的资产定价含义，在美国股市通过构建买入低现金周转期的公司股票，做空高现金周转期公司股票的零投资组合，可以获得每年5%—7%的超额收益，并且验证了现金周转期异象与其他异象的不同。Lin 和Lin基于自下而上的1976—2018年公司层面现金周转期构建了市场总现金周转期指标，对美国股票市场收益的可预测性进行实证评估，发现总现金周转期是一个强有力的正向预测因子。

国内对于现金周转期的研究主要集中在财务分析和公司治理方面，对于中国股票市场是否存在现金周转期异象没有涉及。相较于美国等发达的资本市场，中国A股市场作为一个新兴市场，在制度、交易方式等多个方面皆有着显著的差别，Liu等也指出中国A股市场特有的IPO监管造成了壳价值问题，使得很多美国市场中有效的定价因子在国内市场并不能取得理想的结果。鉴于此，本文拟考察现金周转期在中国A股市场中对资产定价的影响。

本文的学术贡献主要体现在以下两个方面：第一，本文首次尝试检验中国A股市场中是否存在现金周转期异象，结果发现中国A股市场中存在现金周转期异象，但与美国股票市场的情形相反，中国A股市场中公司现金周转期与其股票收益率之间呈正向关系。第二，本文首次尝试从风险因素定价和行为金融两个视角给出中国A股市场中现金周转期异象的成因解释。另外，本文考虑加入了反转因子验证错误定价解释模型的结果。

二、研究设计

（一）现金周转期指标的度量及其简单分析

现金周转期由三个部分组成：存货周转期、应收账款周转期和应付账款周转期。下式是现金周转期的一个被普遍接受的公式：

但是每个组成部分并没有标准化的计算方法，有的研究者使用期初和期末的均值进行估计，也有研究者使用期末值进行估计；估算的会计数据通常出现在公司的年度财务报表中，研究人员和从业人员会使用360天或365天的参数进行折算。由于不同方法估算的差值较大，同一公司在同一时期的现金周转期使用不同的方法计算可能有明显差异。因此，本文使用统一的公式和参数进行计算，即：

本文将依次计算样本总体、行业和公司的现金周转期。

⒈ 现金周转期的变动趋势

图1 为现金周转期及其组成部分：存货周转期、应收账款周转期和应付账款周转期的时间序列均值，单位为天，由于计算所用的数据是财务数据，对应的样本期间为2008—2017 年。变量均在1%水平上进行缩尾处理，但未对行业调整，横轴为年份。可以发现，现金周转期的变动趋势几乎完全是由存货周转期相似的趋势所驱动的。存货周转期并没有较为明显的变动，这与运营管理方面的文献结论一致。根据 Rajagopalan 和 Malhotra的研究，由于现代存货管理工具的发明和使用，如电子数据交换在20世纪80年代初被大量投入使用，一方面，存货周转期在20世纪80年代初到21世纪初存在明显的下降趋势，而在21世纪初后存货周转期的下降趋势消失，变动也不大，本文的样本起始于2008年，所以变动并不大。另一方面，应收账款周转期和应付账款周转期共同变动，其中的原因是公司的应收账款必须是其他公司的应付账款。

图1 2008—2017年现金周转期及各部分变化趋势

⒉ 现金周转期的行业差异

根据证监会分类分别计算各个行业的现金周转期及相关指标。由于样本期内证监会行业分类出现变更，因而分别使用2001版证监会行业分类和2012版证监会行业分类分别统计了2008—2011年和2012—2017年的样本。本文计算了现金周转期中位数的时间序列均值代表各个行业的现金周转期，用以比较行业间的差异；再计算了现金周转期的第一个四分位数和第三个四分位数，用以比较行业内存在的差异；最后计算存货周转期的中位数、应收账款周转期的中位数以及应付账款周转期的中位数，用以检验前文的一些结论。

结果表明，现金周转期在行业间和行业内部都存在显著差异。在住宿和餐饮业中，现金周转期为-17天，而在2012—2017年的房地产业，有近三年半（1 301天）。现金周转期的三个组成部分在不同的行业之间也存在很大的不同，其中存货周转期对现金周转期的影响最大，验证了图1的结果。现金周转期的第一个四分位数和第三个四分位数差异在教育业差距最小，为54天，而在房地产业差距最大，为1 164天，Ramey认为，行业间现金周转期长度的差异主要是技术引起的，所以在接下来的分析中，本文根据现金周转期的中位数和标准差来调整公司的现金周转期——每年通过公司现金周转期减去对应行业现金周转期中值再除以行业现金周转期标准差来调整公司的现金周转期。后文中也将行业调整后的现金周转期称为现金周转期。

（二）控制变量选择与度量

为了检验市场上的异象如规模异象、价值异象等能否解释现金周转期异象，本文选择了相对应的指标作为控制变量，具体构造方法如下：

市场系统性风险。本文用过去24个月的股票月收益率计算得出的该股票值。

公司规模，代表规模异象。本文取公司在t-1月末的总市值的对数。

账面市值比，代表价值异象，本文表示为。本文取公司的资产总计除以总市值后的对数。

非流动性指标，代表流动性异象。本文表示为。参考Amihud的非流动性测度，本文用t-1月的股票日涨跌幅绝对值与日交易股数之比的平均值，该指标越大，股票流动性越差。股票i在第t日的非流动性指标，如式（3）所示：

资产增长率，代表资产增长异象。资产增长率是连续两个财年之间总资产增长的百分比。

盈利能力指标（。基于现金的营运盈利能力指标，本文表示为。Ball等的研究表明，在解释股票收益的横截面时，的表现优于其他盈利能力指标。公式参考了Du等计算中国公司的计算方法：

应计项目，代表应计异象。参考国泰安数据库的方法，公式为：

（三）样本选取与数据来源

本文基于中国市场作为研究对象，选取了在深沪两市的全部A股上市公司，研究期间为2009年5月至2019年4月。本文研究的是现金周转期的资产定价能力，故本文的被解释变量为股票月收益率。本文的解释变量为现金周转期等指标。

本文使用的股票数据，包括月个股回报率，月个股总市值，月无风险收益率以及部分财务数据来源于CSMAR数据库；财务数据中的存货、应收账款净额、应付账款、营业成本、营业收入等来源于WIND数据库和CSMAR数据库。其中，对不满足条件的数据进行了剔除。剔除流通市值在每一期样本底部30%的股票，避免股票价值受到壳价值的污染，这里参考了Liu等对中国股票市场异象研究的方法；剔除所有金融行业的股票；选择剔除上市一年内的股票，考虑到IPO效应，公司上市后经营业绩相对于IPO之前会出现显著下滑的趋势，也可能出现会计操纵等情况；剔除账面市值比为负的股票；剔除ST状态的股票；剔除月度市场交易数据丢失，年度财务数据中市值丢失和现金周转期丢失的股票。

本文参考Fama和French的方法，选择跨四个月将年度财务数据与股票月度数据相匹配，例如2008年度的财务数据与2009年5月—2010年4月的股票收益数据相匹配。

本文对股票收益的分析始于2009年5月，使用2008年度财务数据，结束于2019年4月，使用2017年度财务数据，样本涵盖120个月。为避免极端值的影响，将包括现金周转期、总资产、盈利能力指标、应计项目等财务指标逐月在1%的水平上进行缩尾处理。

（四）研究方法

⒈ 组合价差法

组合价差法是实证资产定价中被广泛使用的一种统计方法，被应用于检验一个或多个变量对股票未来收益的预测能力。方法是根据变量的不同水平将股票进行分组，以形成不同的股票组合，然后检验股票组合的收益情况。组合价差法的优点在于它是一种非参数技术分析的方法，这意味着本文不需要对待检验的变量在横截面关系上提出假设。

本文采用基于单变量的资产组合分析法，首先计算周期性断点，即在每个月计算将样本进行分组的断点值，然后使用这些断点值对样本分组计算平均收益率。本文使用现金周转期升序将样本分为十组，计算每个月十个投资组合的收益率均值，本文将分为等权重均值和市值加权均值两组计算，平均值的计算方法如下：

其中，是收益率，是权重，等权重时。通过检验收益率平均值的单调性，若出现单调或接近单调的模式，就是一个表明组合差异的结果可信的有力证据。另外，本文还计算了现金周转期最高的一组与现金周转期）最低的一组的收益率平均值的差值。通过T检验来确认组合差异在时间序列上的均值是否在统计意义上显著不为0。

⒉ Fama-MacBeth回归

本文以常用的方式进行了Fama-MacBeth 回归。开始于2009 年5 月到2019 年4 月结束的每个月，在横截面上使用每个公司的股票收益对当月现金周转期进行回归，再依次加入了其他控制变量进行回归，在时间序列上得到各个指标的平均系数以及t统计值，以此观察控制了市场其他异象或资产定价指标后，现金周转期异象是否依然存在，也可以说明现金周转期异象能否被其他异象解释。具体的回归方程如下：

其中，式（7）r为i 公司在t 月的股票收益率，CCC为当月该公司的现金周转期；式（8）Beta为市场风险，Size为公司规模，BM为账面市值比；式 （9）ILLIQ为非流动性测度；式（10）Assetgrowth资产增长率，CBOP为盈利能力指标，Accruals为应计项目。

三、实证分析

（一）变量描述性统计及相关性分析

表1 是主要变量以及Fama-French 三因子模型、五因子模型中的各个因子的描述性统计。其中，财务数据来源为上市公司的年度财务报表，本文使用2008—2017年的年度报表，逐年将现金周转期、资产增长率、盈利能力指标、应计项目以1%的水平进行缩尾处理，以减轻异常值的影响；现金周转期是经过行业中值和行业标准差调整后的结果；公司规模和账面市值比是取其自然对数的数值，得到各统计量的时间序列后再求得时间序列均值；是市场因子、是规模因子、是价值因子、是盈利因子、是投资因子，因子后的数字代表对应的三因子模型或五因子模型。经过行业调整后，现金周转期的平均值为0.321，标准差为0.695。非流动性测度的样本内差异最大，其计算公式中，分子为累计日涨跌幅的绝对值，所以最小值为0是合理的。

表1 整体样本描述性统计

表2 是经行业调整后的现金周转期与其他变量的spearman 相关系数及sig 值，其中，sig 值＜0.001 时 sig 值计为 0.000。现金周转期与相关性系数为-0.225，sig 值为0.000，结果在1%水平上显著，系数为负表示现金周转期增加时，趋向于减少；现金周转期也与应计项目呈正相关，上述结果都与前人的研究一致，表明了高现金周转期公司经营盈利能力应当低于低现金周转期公司。现金周转期与其他变量的相关系数均小于0.10，这些指标与现金周转期的关系都比较弱。

表2 变量之间的相关性

（二）组合价差法实证结果

本文按组合价差法进行了十分位的时间序列计算。从2009年5月开始到2019年4月结束的每个月月初，本文根据行业调整的现金周转期将股票分成十组，然后计算下个月每个现金周转期十分位投资组合的超过无风险收益率的超额收益，再使用这些时间序列收益来计算整个样本周期内每十分位组的平均超额收益率，其中包括了等权重投资组合EW和价值加权的投资组合VW。

本文还计算了两个极端的十分位投资组合，即第10组高现金周转期公司股票形成的投资组合以及第1组低现金周转期公司股票形成的投资组合的收益差。为了检验在控制风险因素后，组合的收益差是否还能持续，以高—低组的收益率差为被解释变量，带入Fama-French三因子和五因子定价模型中，分别回归得到系数和常数项，以及对应的t值。常数项阿尔法被解释为组合的平均异常收益，该收益不是由于对选定因子模型中的因子具有敏感性引起的。为了检验组合是否产生统计意义上显著的平均异常收益，使用常数项对应的t统计量。而系数是组合收益率对相应因子的敏感性，系数及对应的统计量可以确定哪些因素与组合的收益相关，如表3所示。

表3 组合超额收益以及定价模型下的异常收益 单位：%

表3的第2行和第3行数据为各现金周转期分组下的各组平均超额收益率以及t值，可以看出，无论是等权重还是市值加权构造的投资组合，收益率整体上呈现递增的趋势。其中，重要的是高—低组，结果表明高现金周转期公司的股票的表现优于低现金周转期公司的股票，市值加权下买入最高现金周转期十分位组股票，卖空最低现金周转期十分位组股票的零投资组合的超额收益为1.035%且在1%的水平下显著，这意味着最高现金周转期十分位组的公司股票比最低现金周转期十分位组的公司股票表现年均要好12.42%。Fama-French 三因子模型和Fama-French 五因子模型下的阿尔法都略低于高—低组的超额收益，说明因子调整减小了异常收益的大小，但结果依然是显著的。另外，在超额收益方面，三因子模型和五因子模型的阿尔法值在市值加权下的高—低组合收益差要大于等权重的高—低组合收益差。

表4是高—低组合收益差在Fama-French的三因子、五因子定价模型上的因子系数，同样分为了等权重组合和市值加权组合。从表4可以看出，三因子和五因子模型下的规模因子系数为正，代表现金周转期异象可能受到规模效应的影响；三因子模型下的价值因子系数为负，与表2中现金周转期与账面市值比的负相关是一致的。

表4 高—低组合收益差的因子系数

（三）Fama-MacBeth回归分析

使用基于行业调整的现金周转期构造投资组合，本文发现投资组合之间的收益率的差异，但由于组合价差法可能受到分组方法等因素对结果产生影响，且并不能准确反映特征变量和股票预期收益的线性关系，因而还需要更加可靠的方法检验现金周转期异象的存在性。由于本文选取的样本在每个月的个数和时间序列长短都不相同，本文借鉴Fama-MacBeth的方法，在横截面上使用每个公司的股票收益对现金周转期进行回归，再依次加入了规模异象、价值异象、流动性异象、资产增长异象、应计异象对应的变量和其他资产定价相关的指标进行回归。表5是对月股票收益率的各个控制变量的回归结果，主要包括了系数的平均估计值以及Fama-MacBeth回归对应的t值。

表5 Fama-MacBeth回归结果

在表5（1）中将现金周转期作为单独的回归预测因子来对公司的月收益进行回归研究。现金周转期的系数为0.260且在5%的水平下显著，体现了现金周转期与组合超额收益率正相关的关系，说明现金周转期越高的公司，股票的收益率越高。

在表5（2）中加入市场系统性风险、公司规模以及账面市值比作为控制变量后，现金周转期的系数为0.155，t统计值为1.658，系数和t值都有所下降，但依然在10%的水平下显著，说明控制规模异象、价值异象后，现金周转期异象依然是显著的；在表5（3）中加入非流动性测度，回归结果表明现金周转期的系数为0.158，对应的统计值为1.693，结果依然显著，说明流动性异象无法解释现金周转期异象；在表5（4）中加入资产增长率、盈利能力指标以及应计项目作为控制变量现金周转期前的系数依然显著为正，说明这些异象都无法解释现金周转期异象。

（四）稳健性检验

本文使用三种方法进行稳健性检验：第一种方法为控制公司规模对分组收益结果的影响，在组合价差法的基础上每年按公司规模将样本分为五组，再在每一个公司规模组中，根据现金周转期将股票分为十组，回归结果表明，大公司和小公司都更容易受到现金周转期异象的影响；第二种方法考虑的是根据国内对于现金周转期的研究在样本选择时通常为制造业或全样本，本文对制造业和非制造业的股票进行分组分析考察结果，结果表明，现金周转期对股票收益的预测能力在制造业或非制造业都很普遍；第三种方法使用组合价差法构建投资组合，本文使用了经过行业中值以及行业标准差调整的现金周转期为分组指标，具体方法为通过年度财务报表计算行业和公司现金周转期后，逐年计算出行业中值以及行业标准差，通过现金周转期减行业中值后再除以标准差得到行业调整的现金周转期，再在总体样本上按1%进行缩尾处理。但是对于现金周转期的分析发现现金周转期在各个年度都会有较大的变化。本节通过调整了现金周转期的计算方式，除了通过行业中值和标准差外，逐年对现金周转期进行缩尾处理，以减少年份对结果的影响，回归结果表明在等权重投资组合下高现金周转期公司的股票组合收益依然要高于低现金周转期公司的股票组合收益，证明在控制了年份的影响后现金周转期异象依然存在。

四、现金周转期异象的成因解释

（一）基于风险的解释

⒈ 基于时变风险的解释

Whitelaw对美国股票市场的研究，通过票据—国库券息差、国债利率、股息收益率和Baa与Aaa债券收益率差四个指标评估了时变的市场风险；林晓明等的研究认为Baa与Aaa级债券收益差对于中国市场影响较小，并且证券评级数据可以查到的起始时间较晚，故舍弃了这一解释变量，参考Wang估计一个考虑时变系统性风险的Fama-French五因子模型：

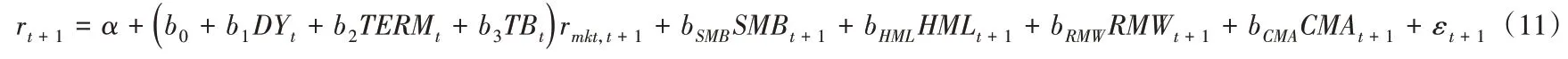
其中，r为月度的低现金周转期—高现金周转期组合超额收益率；r为市值加权市场指数的超额收益；SMB等为Fama-French五因子的另外四个因子；DY、TERM、TB分别为沪深300指数的股息收益率、10年期国债和3个月期国债的收益率差、3个月到期国债的收益率。若考虑时变的因子定价模型可以解释现金周转期异象，则估计的阿尔法值应该为零，结果如表6所示。

表6 时变风险的Fama-French五因子模型回归结果

由表6可知，（2）中市值加权投资组合下的阿尔法值为0.954%，且=2.811，显著不为0，而等权重投资组合下的虽然也不为0，但是不显著。同时b、b、b都与0没有显著区别。这表明，虑时变系统性风险的Fama-French五因子模型并不能解释现金周转期异象。

2. 基于融资风险的解释

本文研究了高现金周转期组与低现金周转期组的收益差是否可以用融资风险来解释。现金周转期较长的公司通常更依赖外部融资来获得营运资金，他们的业绩也可能对金融中介行业的健康状况更为敏感，Almedia等认为资金流动恶化会使公司难以获得外部融资，在到期债务展期时可能遭受损失。现代金融理论认为，随机折现因子（Stochastic Discount Factor，SDF）能决定资产价格，而随机折现因子通常与总财富的边际价值相关。许多资产定价研究通过测量投资者的边际财富价值来确定随机折现因子，但这是建立在一系列假设之上的。根据中介资产定价理论，金融中介通常进行众多投资交易，他们的交易策略更加复杂，运用的模型更精准，而交易费用低，频率高，所以金融中介的随机折现因子可以一定程度上解释资产的超额收益。Adrain等认为，金融中介的杠杆率可以反映偿债能力，融资条件较差时，资产风险增大，要求的收益也增加。

本文选取了He等提出的中介资本比率因子，以及Adrain 等提出的金融中介杠杆因子作为金融中介的随机折现因子。如果融资风险可以解释现金周转期异象，那么高现金周转期公司应该与这些因子更加正相关。除此之外，还选取了市场风险相关的指标，即BAB因子（Betting Against Beta）进行回归，结果如表7所示。

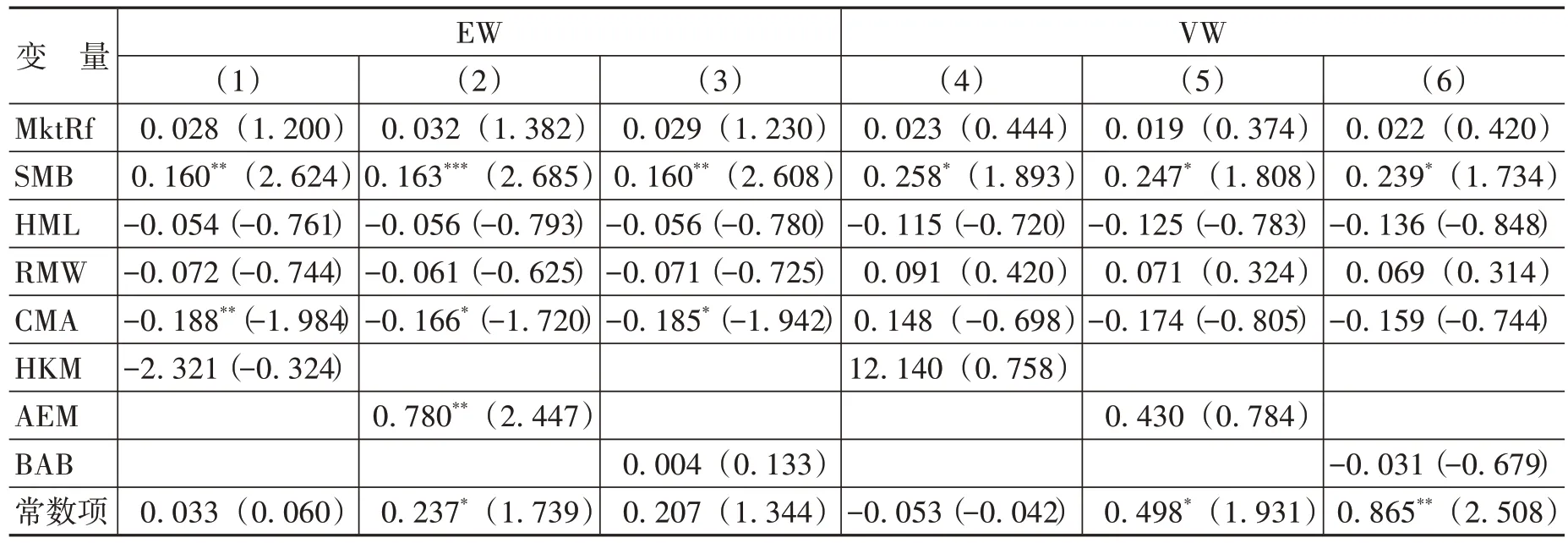
表7 使用随机折现因子扩展的因子模型对CCC高—低投资组合收益回归结果

（二）基于错误定价的解释

⒈ 错误定价的解释检验

虽然融资风险被证实可以在一定程度上解释现金周转期异象，不过可能并不充分，现金周转期异象是否由风险和错误定价共同产生的，还需要进一步对错误定价相关指标进行研究。现金周转期作为衡量管理层使用营运资金的效率的指标，与公司盈利能力相关。通常来讲，大多数人认为高现金周转期公司的盈利能力较差，使投资者对其股票有较低的估价，而低现金周转期公司的盈利能力更强，使投资者对其股票有较高的估价。投资者也许不能完全解释现金周转期对盈利能力的影响，或者对现金周转期过于敏感。本文参考Hou等使用的横截面模型，估计一个回归：

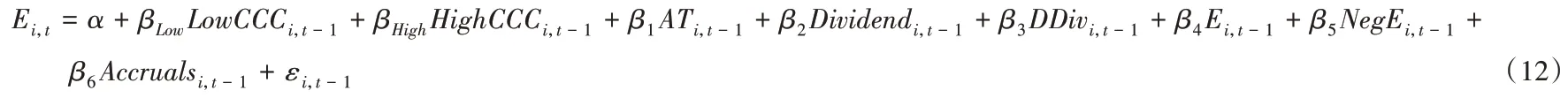
其中，E为i公司季度的收益除以总资产，参考Wang的方法，将收益定义为公司基于现金的盈利能力指标，同时参考Du 等对中国A 股市场的计算方法进行构建，和分别表示最高和最低的现金周转期十分位数，AT为总资产，为前一年支付的股息除以总资产，为是否支付股息的虚拟变量，支付则为0，未支付为1，为负收益公司的虚拟变量，正时为0，负时为1，为应计项目，所有解释变量都是季度来计量的。若现金周转期能够提供对公司未来收益的预测能力，本文预计为β应当低于β，那么错误定价可以解释现金周转期异象。如表8所示，在（1）中以CBOP为被解释变量，上一期的最高和最低现金周转期十分位数为解释变量进行回归，发现的系数为-0.003（值为-9.963），而的系数为-0.0002（表8中保留3位小数）（t值为-1.988），的系数显著低于的系数。在（2）中，本文控制了资产、股利和应计项目等相关变量后，系数依然显著低于的系数，这与本文的预期一致。投资者错误估计了现金周转期对公司收益的影响，导致低估了高现金周转期股票，高估了低现金周转期股票，从错误定价的角度解释了现金周转期异象。

表8 现金周转异象包含的未来盈利信息的测试结果

⒉ 使用反转效应检验错误定价的解释

股价变化可以分为基本面与情绪面两部分。基本面部分包括了上市公司的经营状况，也包括经济环境、市场流动性等因素，其会对上市公司的实际价值产生影响，也是股价变化的趋势项。情绪面包括市场风险偏好等对信息的反应程度等交易层面的因素，其并不影响上市公司的实际价值，但对股价产生巨大的影响，故将其看作股价的暂时性扰动。动量效应和反转效应就是由于市场对信息的敏感性产生的。若市场对利好反映不足，则出现动量效应，若市场对利好反应过度，则随着市场情绪的稳定，股价会回落，呈现反转效应。

美股与A股市场股价呈现了两种截然不同的形态。美股的主要参与者是机构投资者，具有低换手、注重基本面估值的特点，公司真实的盈利变化是驱动美国股价变动的主要因素。加之美股市场的上市公司数量众多，投资者对信息存在明显反映不足，在利好或利空出现时，股票价格往往难以一步到位。在中国A股市场，个人投资者是主要参与主体，具有高换手，重消息，追涨杀跌的特点。A股市场对信息往往反应过度，伴随着股价过度涨跌，反转现象在A股市场屡见不鲜。

如表9所示，本文以高—低组合收益差为被解释变量，Fama-French的市场因子，规模因子，价值因子，盈利因子，投资因子，加入反转因子为解释变量，解释现金周转期异象的产生的原因。同时在等权重和市值加权的投资组合收益率差下，反转因子都具有显著为正的系数。这表明投资者高估了低现金周转期公司的股票而低估了高现金周转期公司的股票，即错误定价导致了现金周转期异象。

表9 加入反转因子的现金周转异象高—低组合收益的解释

（三）中美股票市场现金周转期异象差异的原因讨论

通过分别讨论风险因素和错误定价对中国A股市场的现金周转期异象产生的原因。其中风险因素考虑了时变风险和融资风险的影响，结果表明时变风险不能解释中国的现金周转期异象，而融资风险可以部分地解释现金周转期异象。错误定价的两个测试与中国A股现金周转期异象的错误定价解释是一致的。两方面的解释并不是全面的和决定性的，且不能通过一种解释排除另一种解释，可能风险和错误定价两种力量都对现金周转期异象产生了影响。Wang的研究表明，美国股市的现金周转期异象可以通过错误定价进行解释，而时变风险与资金风险都不能解释美国股市的现金周转期异象。在与本文相似的错误定价模型中，美国股市的研究结果表明的系数为正，系数为负，并且在加入变量控制过去的收益后结果依然显著。这一结果说明现金周转期对中国A股市场和美国股市有着相反的影响，最终结果都导致了投资者的错误定价。

五、结论与讨论

本文以中国A股市场为研究对象，选取2009年5月至2019年4月的市场交易数据及对应的财务数据，通过组合价差法和Fama-MacBeth回归方法在月度频率上发现了中国A股公司层面的现金周转期异象，并使用考虑风险的因子定价模型和错误定价模型探讨了中国A股现金周转期异象的成因及解释。本文的主要结论有以下两点：首先，高现金周转期公司的股票比低现金周转期公司的股票获得更高的收益。同时，根据Fama-MacBeth回归的结果，发现现金周转期异象不能被其他异象解释，即现金周转期指标拥有独立的收益预测信息。其次，进一步探讨中国股市的现金周转期异象的成因及解释，本文发现现金周转期异象不是源于时变风险，而是融资风险以及错误定价。

本文选择了金融中介杠杆因子作为衡量融资风险的指标，分析结果发现高现金周转期股票对金融中介杠杆因子的敏感性较高，说明高现金周转期公司的股票风险更大，收益也应当更高，与本文的研究相一致；在错误定价模型中，发现投资者会低估现金周转期较高的公司股票，未来有较高的收益率，高估现金周转期较低的公司股票，未来有较低的收益率。在进一步检验错误定价模型的解释中，加入了考虑反转因子的因子定价模型，反转因子显著的正系数验证了错误定价的结论。第三，本文还证实现金周转期在行业间和行业内都存在巨大差异，现金周转期的时间序列变化主要是由于存货周转期的变化。

基于上述结论，本文认为：公司管理者应当更加理性地认识现金周转期对公司盈利能力和融资成本的影响，使公司得以平稳运行；投资者可以积极关注高现金周转期股票组合，考虑盈利能力被低估的股票，这样有助于防范风险并提升投资组合的业绩。中国股市现金周转期异象的存在，导致传统的因子定价模型解释力下降，但这并非对有效市场假说和因子定价模型的否定。一方面，当异象被发现新的交易策略公布后，使用更新的数据检验大多数异象会减弱或消失，说明通过投资者的行为使得市场有效性得到了提升，市场在长期将是有效的；另一方面，中国股市现金周转期异象的发现，也可以一定程度上揭示传统的因子定价模型在拥有独特经济和金融体系的中国市场下的不足之处，有助于理论和模型的进一步完善。