基于课程体系的原码、反码和补码教学研究
向继文

关键词:课程体系;C无符号数;带符号数;原码;反码;补码
中图分类号:G642 文献标识码:A
文章编号:1009-3044(2022)36-0154-03
1 引言
在《数字电子技术基础》《微机原理与接口技术》《汇编语言程序设计》等课程中,数制系统都是非常重要的内容,是要求学生理解和掌握的重要知识点[1]。对于学习高级语言程序设计的学生来说,掌握好数制系统也有利于更深入地理解和分析程序对数据处理的实质。在数制系统中,对学生较难的是原码、反码和补码,也是数制系统教学的重点和难点。经过多年的研究与实践,对原码、反码和补码的教学取得了一定的经验,提出了基于课程体系的原码、反码和补码的教学观点。文中仅讨论整数的原码、反码和补码的表示及教学方法,小数的表示对大多数专业而言是不需要掌握的,需要处理小数时在汇编语言中可以设计算法用整数模拟小数,或者直接用高级语言处理。
2 无符号数和带符号数
原码、反码和补码是带符号数的表示方法,要掌握好原码、反码和补码知识,首先要清楚无符号数和带符号数的区别,以便正确使用这两类数据。日常生活中,例如:电话号码、房间的门牌号码、计算机内存单元的地址等,这些数值没有数学上的正负含义,是无符号数。但是身高体重之类的数就必须为正数,在银行存取款时,存进去的金额是正数,会使得银行余额增加,取出来的金额是负数,使得银行余额减少,这类数据就是带符号数。
在数字系统中采用二进制数,只要将无符号数用二进制数表示,高位用0补到规定的位数就可以了。带符号数有正负符号,符号要数码化,且有原码、反码和补码多种表示方法,比无符号数要复杂很多。反过来说,学习原码、反码和补码知识就是学习带符号数在数字系统中的表示方法。
此外,如果给出一个二进制数,这个数究竟是带符号数还是无符号数,该怎么看待怎么处理呢?很多学生也是迷惘的。实际上,这个数可以将它视为无符号数,也可以视为带符号数。在汇编语言中,当将这个数看作无符号数时,就用无符号数的指令去处理,将这个数看作带符号数时,就用带符号数的指令去处理,两类数用汇编指令加以区分,分别处理。在高级语言例如C语言中,用数据类型区分。如unsignedchar、unsigned int之类的处理无符号数,用char、signed char、int、signed int之类的处理带符号数。
由于符号位的问题,导致位数相同的二进制数,作为无符号数和带符号数时表示的数值范围是不相同的。例如十六位二进制数,表示的无符号数范围为0~65535,用补码表示的带符号数范围为-32768~+32767。这个特点在数字电子技术、微机原理与接口技术、C语言等课程及各类嵌入式处理器中都是相同的,实现了把多门课程的知识串在一起,有利于学生构建课程体系,打通课程之间的壁垒。
3 原码表示方法
原码是用来表示带符号数的,这就需要将正、负符号数码化。在二进制数的前面增加一位符号位,符号位为0表示这个数是正数,符号位为1表示这个数是负数,这种形式的数称为原码[2]。对原码,可以用数学公式严格定义:一个数连同符号位一起用n位二进制数表示,某一个数X的原码为:
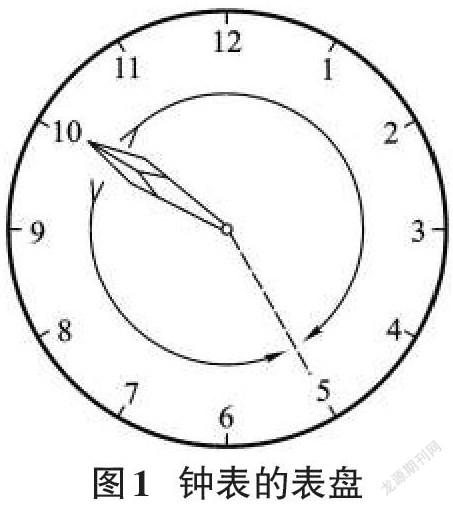
要使学生理解补码的概念及引入补码的优越性,通常从日常生活中的实例入手,常用的一个案例就是钟表,如下图1所示。
表盘上时针指向10点钟,而正确的时间是5点钟,要把时针拨回到5点钟有两种方法:第一种方法是将时针往回拨5个小时指向5點钟,第二种方法是将时针往前拨7个小时指向5点钟。用数学式表示出来,第一种方法为10-5=5;第二种方法为10+7=12+5=5,由于表盘上最大的数是12,当时间超过12点以后,12自动丢失,只保留减去12以后的余数5。从效果上来看,10-5与10+7是等价的,都使时针指向了5点,12 称为模,“模”是指一个计数系统的进位基数[4]。7是-5 对模12的补数,也称为补码。该实例说明了对模12 而言,10-5减法运算可以通过10+7加法运算来实现。这意味着,模确定以后,在舍弃进位的条件下,减去一个数可以通过加上该数的补码来实现,也意味着在电路中,减法运算可以通过加法电路来实现,从而简化了电路设计。
将上例加以拓展,设某表盘有16个刻度,则刻度值为1~16,模为16,刻度0与16是重合的,与上例中0 点与12点是重合的道理相同。在二进制数中,因24=16,即四位二进制数的模是16,依此类推,对于n位二进制数,其模为2n,对于任意负数X,其对于模2n的补码为2n-|X|。
通过对这个实例的分析,可以使学生理解模的概念,补码的概念以及通过补码将减法运算转换为加法运算,有利于简化硬件电路的设计。
5.2 补码的特点
通过分析补码的定义及前面的生活实例,可以得到补码的特点。
(1)最高位为符号位,为0表示这个数是正数,为1表示这个数是负数。
(2)对于正数,[X]=[X],即正数的补码与原码相同,且能表示的数值范围也相同。
(3)对于负数,补码的值等于模减去该数的绝对值,再对照负数补码和反码的数学定义式可知,负数的补码等于该数的反码加1。
(4)对于零,设n=8,则[+0]=00000000,[-0]=00000000,0的表示是唯一的,解决了+0和-0的表示问题。
(5)使用补码表示,可以将真值的减法运算变为机器中的加法运算,从而使CPU内部不再需要设计减法器[5],简化了CPU的设计。
(6)补码表示时,有少数特殊数的补码对学生比较难以理解。如,当n=8时,-128的补码是10000000,当n=16时,-32768的补码是1000000000000000,这些数补码的符号位和数值位合二为一,可以根据补码的定义式来理解,对非计算机专业的学生而言,还可以把这几个数的补码表示简单地看作是一种规定,计算机程序的编译软件也是按这种方法处理的,学生就容易理解了,否则容易造成困惑。
5.3 几个需要说明的问题
(1)补码运算的结果仍为补码,类似于二进制数运算的结果仍为二进制数,不可能变成了十进制数。
如果运算结果的符号位为0,说明结果是正数,该补码值等于其原码,可以由补码值求出真值。如果运算结果的符号位为1,说明结果是负数,要获得其真值,需要由该补码数求出其原码,再依据原码求出真值。
在求负数补码对应的原码时,一般采用的方法是[[X]]=[X],即对负数的补码再求补码,得到负数的原码。有些同学会想当然地认为将负数补码的数值位按位求反,再减去1,这种方法不仅结果错误,而且再一次产生了减法运算。
(2)关于数据溢出的理解
如果做的是有符号数的运算,例如,78-54=24,因78-54=78+(-54),使用补码表示时,设n=8,则有[78]+[-54]=01001110+11001010=00011000,补码运算的结果仍为补码,舍弃进位,符号位为0,说明该补码对应的真值是正数,正數的补码等于原码,故该补码数对应的真值为24,结果正确。
如果没有明确是无符号数或者带符号数运算,该如何判断是否溢出。例如,已知两个二进制数的加法运算,01001110+11001010=00011000,因硬件只有8位,故最高位产生的进位自动丢失,有没有产生溢出取决于如何看待这两个数。在计算机中,如果把这两个数看作是无符号数,则产生了溢出,为了防止数据出错,在CPU的标志寄存器中,设置了进借位标志CF,并置CF=1,编程者要根据CF位进行处理以得到正确的数据。如果把这两个数看作带符号数,在CPU 的标志寄存器中,设置了溢出标志OF,且OF位等于次高位与最高位产生的进位异或运算的结果,即OF=C⊕C=1⊕1=0,故没有产生溢出。
(3)关于数据位数的理解
在数字电子技术课程的学习中,二进制数的位数可以根据需要来设定,没有特别规定。但是,在计算机中是不可以的。例如,5位二进制数,在数字电子技术中可以使用,但是在计算机中不可以采用5位,因为没有字长为5位的CPU。早期有4位的CPU,现在已经淘汰了,现在CPU的字长有8位、16位、32位和64位,这些字长的数据在计算机语言中有相应的数据类型去处理。例如,在C语言中,用char处理8位数,早期用int处理16位数,随着计算机技术的发展,现在的编译软件将int型数据编译成了32位甚至64位,这与编译软件有关。如果只需要使用5位二进制数,该数据也必须采用一个字节或者一个字来存储,然后通过编程来处理这5位二进制数。
(4)关于符号扩展的理解
设有十进制数+23和-23,在数字电子技术中,可以用6 位二进制数表示,其补码分别为:[+23]=010111,[-23]=101001。现要求将这两个数用8位二进制数表示,则有[+23] =00010111,[-23] =11101001;若要求将这两个数用16位二进制数表示,则有[+23] =0000000000010111, [-23]=1111111111101001。比较发现:对于带符号数,当需要将位数较少的补码数采用更多位表示时,只需要将位数较少的补码数的符号位向高位扩展,符号位为0 则向高位补0,符号位为1则向高位补1,补齐到所需的位数即可;对于无符号数,直接在高位补0,补齐到所需的位数即可。
(5)关于补码与求补的区别
某些CPU提供了求补的指令,例如在8086 CPU中提供了NEG指令。假设AL寄存器的值为15H,对AL求补得到EBH,将两个数写成8位二进制数后比较发现,EBH是将15H所有位求反后加1而得,将这两个数看作补码数,15H的真值是21,EBH的真值是-21。假设AL寄存器的值为E9H,对AL求补以后得到17H,将两个数写成8位二进制数后比较发现,17H是将E9H所有位求反后加1而得,将这两个数看作补码数,E9H的真值是-23,17H的真值是+23,可见,执行求补指令可以得到被求补的数据相反数的补码。
假设AL寄存器的值为80H,BX 寄存器的值为8000H,对AL、BX求补以后的值分别为80H、8000H,将这两个数看作补码数,80H的真值是-128,8000H的真值是-32768,符合补码的数学定义式。
结论:已知某个负数X的原码,求其补码时符号位是不变的,如果X是正数,则其补码等于其原码。已知某个带符号数Y,对Y做求补运算,会得到其相反数的补码,即-Y的补码,从二进制运算的角度来看,是将Y的二进制的所有位求反,最后在末尾加1。
6 结语
讨论了在原码、反码和补码知识的教学中,按照无符号数和带符号数的区别;无符号数在数字系统中的表示方法;带符号数的原码、反码和补码的表示方法及其特点;并通过实例分析了如何将所学知识与C语言、汇编语言及相关硬件知识联系在一起,将知识学习放置于由相关课程组成的课程体系背景中,有利于帮助学生建立课程体系的观念,在不同课程之间将相关知识融会贯通,避免了在不同课程中对相同的知识内容割裂开而孤立地学习,从而促进对知识的理解、记忆和应用。

