非高斯噪声背景下无线电协作频谱感知方法

朱兴伟

(安徽医学高等专科学校 公共基础学院,安徽 合肥 230601)

为了满足无线电通信技术在市场内多个行业中的有效应用，提升通信服务的质量，大部分无线电单位在进行频谱分配时会基于静态层面实施或开展工作.但随着无线通信行业的发展，市场内现有的频谱资源呈现一种稀缺状态，尽管技术单位在开展此方面相关研究时，提出了针对此方面的OFDM技术、MIMO技术，相关技术的应用在一定程度上实现了对现有频谱资源利用率的提升，但提出的技术在实际应用中会受到信道容量的限制与约束，效率提升的作用十分有限.为了解决与之相关的问题，美国FCC协会联合了地方高校与有关技术研究部门，对某无线电通信地区进行了频谱实地测量，综合实测与研究结果发现，大部分具有授权使用能力的无线频谱资源在空间中呈现闲置状态，即未能被无线电通信有效使用，前端对频谱资源的使用率仅在25.0%[1].这一现象表明静态频谱调配方式会浪费现有的频谱资源，这也是造成资源稀缺的主要原因之一，为了进一步保证资源的有效使用，应当提升对频谱资源的感知能力.而传统的感知方法会受到无线电通信信道中非高斯噪声的干扰，出现感知能力差、检测性能不佳等问题，为此，本文将以非高斯噪声作为设计背景，结合现有资源的调度与分配方式，设计一种全新的频谱感知方法，以此种方式实现对闲置资源的有效利用，解决频谱资源不足或有效使用率低的问题.

1 非高斯噪声背景下无线电协作频谱感知方法设计

1.1 建立非高斯噪声稳定分布感知模型

为了实现对无线电协作频谱的有效感知，需要在方法设计前，建立一个可用于描述无线电通信信道中非高斯噪声稳定分布的感知模型.在此过程中，可假设无线电通信网络是由一个中心与M个次级用户构成，对应的用户需要通过频率选择的方式，进行主用户信号强度的分析，并将信道进行融合后，将融合结果通过传输信道定向供应给本地前端[2].当本地端完成对结果的融合后，再通过传输决策行为的方式，进行最终结果的判决.在此次协作通信传输方案中，可将信道内的无线电通信信道中的非高斯噪声定义为一个二元假设校验问题，对信道噪声的描述表示为两种，分别为H1与H0，假设存在第m个用户，在对应离散时间点n时，采集到的信道基带信号表示为z，则此时无线电信道中的非高斯噪声可以表示为

(1)

公式(1)中wm(n)表示前端在n时刻信道加性噪声；s(n)表示前端在n时刻发出的无线电信号.在本文中，将s(n)假设为不含未知参数的弱正弦信号，其中未知参数表示为信道相位、信号幅度等，其中n的取值范围为[1～N]，在确保多个携带非高斯噪声的信号呈现相互独立的状态时，可假设噪声值符合零均值，即所有的非高斯噪声在信道中均符合高斯噪声的随机表达方式[3].

假设噪声的序列是以概率分布的方式得到的，则对应的噪声在空间内与样本数量呈一种随机方差关系，此时用于描述高斯信号分布的两个核心指数为噪声方差比与非高斯噪声混合系数，通常情况下，两个参数的取值范围为[20.0～1.0×104]与[0.01,0.33]，输出在此过程中的非高斯噪声密度，将密度值表示为p，对应表达式如下

(2)

公式(2)中ε表示非高斯噪声峰值,σ表示噪声拖尾分布.根据上述计算公式，掌握非高斯噪声在信道中的分布特征，对接不同通信信道的噪声分布，完成对非高斯噪声稳定分布感知模型的构建[4].

1.2 无线电协作频谱能量在线检测

目前，较为常用的检测方法包括似然校验校测法与能量检测法，当无线电通信过程中的主用户信号携带信息，背景噪声满足非高斯噪声分布特征时，优选能量检测法.此种检测方法是一种非相对感知的方法，检测中信号可以通过能量的方式进行表达[5].检测时，截取一段频谱时域，将此区段接收到的信号总能量作为检测量，检测量与预设信号能量值进行比对，通过此种方式，掌握信号携带的能量值是否能满足前端通信需求.此过程可用下述图1所示的流程表示

图1 无线电协作频谱能量在线检测流程

检测时，先将对应的信号传输到低通结构的滤波器中，通过此种方式去除滤波器的外带噪声与邻近信号，再通过模拟信号转换的方式将对应信号表示为数字信号，输出信号后，得到一个针对信号的统计量T，将T与η门限值进行比对，若统计后的结果T>η，则证明前端存在主用户信号;反之，统计后的结果T<η，则证明前端不存在主用户信号[6].按照此种方式，进行无线电协作频谱能量的统计量的计算，对应T的计算表达式如下

(3)

公式(3)中T表示协作频谱能量的统计量,z(n)表示在n时刻信号在空间中的离散序列.输出对应的协作频谱能量统计量结果，对其进行离散处理，但考虑到离散处理过程中，能量携带的性能极易受到噪声与相关不确定因素的影响出现检测结果偏离的问题[7].例如，在非高斯噪声信噪比过低时，信号极易受到非高斯噪声的干扰而被削弱.当出现此方面问题时，需要对信号进行离散化处理，确保信号的离散值大于样本值，确保信号更好地被剥离，以此种方式提高检测信号与实际信号的匹配度，实现对无线电协作频谱能量的在线检测.

1.3 设定无线电协作频谱感知门限

结合已知的无线电协作频谱能量，设定一个感知门限确保感知结果与实际结果的匹配性.在此过程中，需要先设定一个针对感知结果的虚警概率指标，并认为只要无线电通信传输信道内存在噪声信号，对应的前端数据融合中心便可以实现对频谱能量值的感知，由公式(3)对存在非高斯噪声的无线电协作频谱感知过程进行描述，计算公式如下

(4)

公式(4)中Y0表示存在非高斯噪声的无线电协作频谱感知过程,i表示感知行为发生次数,M表示数据中心,C0表示信号离散值.为了确保设定的感知门限在实际应用中具有一定实用性，需要设定一个虚警概率参数μ，μ的使用需要满足二次项分布特征，对应的μ方差表达式如下

μoi=E=MC0，

(5)

公式(5)中μoi表示为虚警概率参数的方差计算结果,E表示虚警概率参数均值结果.在此过程中假设M符合最大极限值标准，可以根据中心极限理论，进行虚警概率参数的统计，将统计结果与非高斯噪声分布进行对接，得到一个实际高斯分布值.在此基础上，假设A表示无线电协作频谱感知门限，可采用对A进行建模处理的方式，对A进行的一阶求导，求导后得出一个对应无线电协作频谱感知通道的门限值，但无线电通信是一个多向对端通信的过程，要解决在此过程中的门限值单一问题，需要进行通信信道中漏检概率的分析[8].假设无线电通信信道表示为AWGN，则此信道对应的漏检行为发生概率可以表示为

(6)

公式(6)中Pm表示漏检行为发生概率,Q表示下信道漏检行为发生概率,τ1表示衰落信道漏检行为发生概率.根据不同信道漏检行为发生概率，进行门限值的上调或下调，直到设定的门限值可以满足实际计算需求，此种确保设定的最终结果可以满足无线电协作频谱感知需求.

1.4 基于低阶分数的无线电协作频谱感知结果融合

在掌握了无线电协作频谱感知门限后，从低阶分数计算角度进行无线电协作频谱感知结果的融合处理.在此过程中，需要先进行无线电通信前端发射信号的稳定性分析，假设信号表示为κ，当κ在空间中的分布具有低阶统计特征时，可以直接通过稳定性分析的方式对κ在空间中数值的统计与对接.在大部分条件下κ在空间中是不满足上述提出的分布要求的，因此，需要在融合感知结果前，设定一个数据融合中心，根据不同通信信道中κ的统计量与分布趋势进行κ值的分布二次统计.完成对参数值的统计后，根据感知结果在空间内的离散分布形式计算不同无线电信道中κ的分散系数，按照对应的系数比例，进行不同信道感知信号值的融合，将融合结果作为本文设计方法的最终感知结果,输出结果后，即可认为实现了对无线电协作频谱的感知.上述提出的过程，可用下述计算公式表示

κ2=MN[C(2P,α)](C(P,α)γ2P)，

(7)

公式(7)中κ2表示无线电协作频谱感知结果的平方值,γ表示信号低阶分数表达方式.按照上述计算公式，输出κ2的具体计算值，将计算机进行开平方处理，得到|κ|值，将此数值作为无线电协作频谱感知结果.综上所述，实现对无线电协作频谱感知结果的融合，完成基于非高斯噪声背景下无线电协作频谱感知方法的设计与研究.

2 对比实验

为了验证该方法在实际应用中的效果，选择以主用户与次用户之间感知信道无衰落的情况下，通过实验的方式，验证本文提出的方法在实际应用中感知结果的偏移系数，以此实现对该方法感知精度的检验.在实验过程中，假设主用户一方在无线电通信信道当中的信号均值为0，噪声为标准SaS分布，次用户在无线电通信信道中的背景噪音为2，对应的阶数为0.8.假设在实验过程中，选择的无线电协作频谱样本序列长度为1000，利用蒙特卡洛方法对该样本进行1000次的仿真.除此之外，在实验中设置M=1表示为单用户检测，M=2表示为两次用户协作检测，以此达到协作频谱感知的效果.实验过程中各参数的设置情况如表1所示.

表1 各参数设置对照表

结合表1中的数据，将本文提出的感知方法应用到上述构建的实验环境当中，针对本文方法得出的感知结果，对其偏移系数进行计算，偏移系数的计算公式为

偏移系数=感知结果检测概率×感知门限/方差.

(8)

根据上述公式，计算得出感知结果的偏移系数，并将不同采样序列数对应的偏移系数记录，绘制成如表2所示的实验结果.

表2 本文感知方法感知结果偏移系数记录表

从表2中的数据可以看出，在进行五次感知过程中，随着采样序列数的增加，偏移系数呈现出明显的增加趋势，但五次感知结果中偏移系数均未超过0.3000.偏移系数越接近0，则说明感知结果精度越高；反之，偏移系数越接近1，则说明该感知结果精度越低.由此可知,本文提出的无线电协作频谱感知方法在应用到实际中可以将偏移系数控制在合理范围内，满足对无线电协作的高精度感知要求.

为进一步验证本文设计方法的性能，使用文献[2]方法作为对比方法进行实验.此次试验中，在无线电通信环境中随机地增加了恶意入侵节点，其中，恶意入侵节点占总节点数的10%，重复进行5组，每组各10次，测试两种方法的检测概率，结果如下图2所示

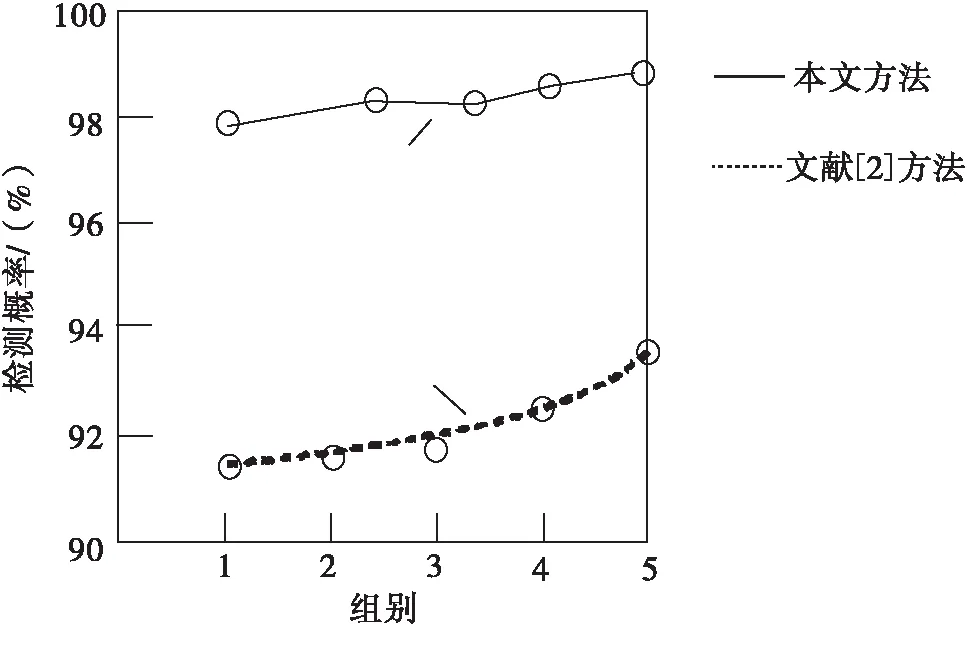
图2 不同方法检测概率结果

分析图2可知，本文方法在感知无线电通信信道中能够有效地检测出恶意入侵节点，平均检测概率为98.7%，远高于其他方法的检测概率92.4%，具有高精度的感知性能.

综上实验过程中，人为引入了背景噪声干扰，但从本文感知方法的应用结果中可以看出，这种干扰并不会对偏移系数造成影响，在噪声当中具备良好的感知性能.其主要原因是噪声不存在二阶以及高阶统计量，并且没有PDF解析式，在对其进行感知时传统基于二阶或高阶统计量的感知防范已经无法适用这种无线电传输环境，而本文提出的感知方法在应用中能够从分数低阶统计量的理论入手，在进行对感知统计量计算时不需要主用户的信号、信道增益的先验信息等.同时，本文感知方法能够根据中心极限定理理论进一步推导出感知信道的在无衰落时的性能，因此本文无线电协作频谱感知方法具有良好的感知性能，并且能够实现对多用户的协作感知，能够有效地降低背景噪音对感知结果造成的影响，从而进一步提高感知性能.

3 结语

本文从建立非高斯噪声稳定分布感知模型、无线电协作频谱能量在线检测、设定无线电协作频谱感知门限、基于低阶分数的无线电协作频谱感知结果融合四个方面，以非高斯噪声作为设计背景，结合现有资源的调度与分配方式，设计一种全新的频谱感知方法.为了验证该方法在实际应用中的效果，选择以主用户与次用户之间感知信道无衰落作为背景进行实验，实验结果证明，此设计的感知方法能够根据中心极限定理理论进一步推导出感知信道在无衰落时的性能，说明了本设计的感知方法具有良好的感知性能，并且能够实现对多用户的协作感知，能够有效降低背景噪音对感知结果造成的影响，从而进一步提高感知性能.但要正式将此方法在市场内进行推广与使用，还需要在后期的研究中，将此方法应用到不同环境下进行测试，通过多次测试后证明本文方法真实有效，才能逐步将其投入使用.