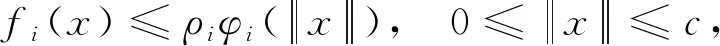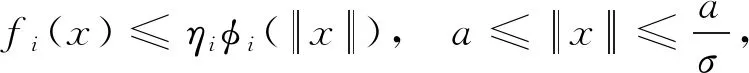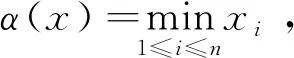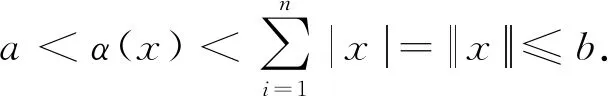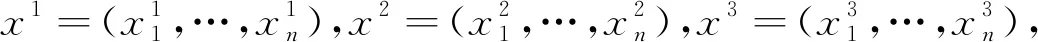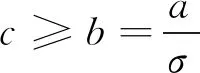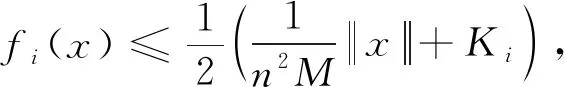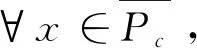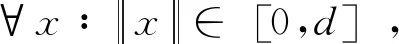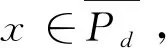一类代数系统的多重正解的存在性与特征区间
赵 进,丁伯伦,李文娟
(1.扬州工业职业技术学院 基础科学部,江苏 扬州 225100;2.上海师范大学 数理学院,上海 200234)
考虑如下一类非线性代数系统
x=AF(x),
(1)
其中x=(x1,x2,…,xn)Τ,A=(aij)n×n是n×n矩阵且aij≥0,(i,j)∈[1,n]×[1,n],F(x)=(f1(x),f2(x),…fn(x))Τ,这里用[1,n]表示集合{1,2,…,n}.
代数方程起源于许多不同的研究领域,其中差分方程、边值问题、动态网络、随机过程、数值分析等领域中的许多问题都可以转化为系统(1).由于这些广泛的应用,在最近的二十年里,非线性代数方程(系统)正解的存在性问题被广泛地研究,可参考文献[1-3].例如,在文献[2]中,Zhang 以及合作者考虑了如下系统
x=λAF(x)
(2)
存在性问题.在非线性项是超线性或次线性的前提下,利用Krasnoselskii不动点定理得到了系统(2)正解的多重性结果.
事实上,大部分的代数系统解的多重性结果都是根据不动点定理研究得到的,例如锥不动点定理、Schauder不动点定理、Krasnoselskii不动点定理等.本文主要根据Leggett-Williams不动点定理建立代数系统(1)的存在性与多重性理论.在过去的几十年里,Leggett-Williams不动点定理被广泛地运用于边值问题解的存在性与多重性的研究.例如,文献[4]研究了Monge-Ampere方程的Dirichlet边值问题,文献[5]研究了在Minkowski空间中平均曲率方程的奇异边值问题.
作为新结果的应用,以上方法可以刻画系统(2)的特征区间,其中λ>0是一个正参数.此外,本文证明了在给定的特征区间内,系统(2)至少存在三个正解.
1 预备知识
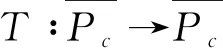
(i){x∈P(α,a,b)∶α(x)>a}≠∅且对于∀x∈P(α,a,b),都有α(Tx)>a;
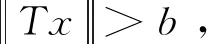
则算子T至少存在三个不动点x1,x2,x3且满足
在以下讨论中,假设A≥0,即对于∀(i,j)∈[1,n]×[1,n],都有aij≥0,且要求矩阵A的每一列至少存在一个正元素.此外,令
(3)
为了运用引理1处理系统(1),取X=Rn并且定义锥
其中σ在(3)式中被定义.定义算子
其中
(4)
不难发现,求解问题(1)等价于寻找(4)的不动点.假设
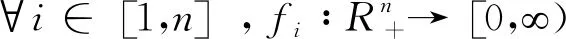
引理2假设(H1)成立,则T[P]⊂P且T∶P→P是紧算子.

从而
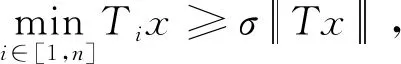
2 主要结论
运用引理1建立系统(1)至少存在三个正解的多重性结果.
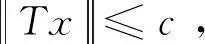
定理1假设(H1)成立,且假设存在常数a,c,d满足0 (H2) 对于∀i∈[1,n],都存在常数ρi>0及连续非减函数φi∶[0,∞]→[0,∞]使得 (H3) 对于∀i∈[1,n],都存在常数ηi>0及连续非减函数φi∶[0,∞]→[0,∞]使得 则系统(1)至少存在三个正解. 因此,可以得到{x∈P(α,a,b)∶α(x)>a}≠∅.对于∀x∈P(α,a,b),则有 定理2假设(H1)和(H3)成立,且满足以下条件 则系统(1)至少存在三个正解. 可知 因此引理1中的条件(ii)成立.其余证明类似于定理1的证明,省略. 应用定理2,很容易刻画系统(2)的特征区间,并且得到如下结果. 系统(2)至少存在三个正解.