区域物流与新型城镇化发展互动关系测度

吴 彪，尹 静，柏寒茁，刘 拓，邵明晖

(1.黑龙江工程学院 汽车与交通工程学院, 黑龙江 哈尔滨 150050；2.东北林业大学 交通学院，黑龙江 哈尔滨 150040；3. 黑龙江工程学院 经济管理学院，黑龙江 哈尔滨 150050)

0 引言

区域物流与新型城镇化是区域经济社会发展的重要组成部分，二者之间存在交互作用关系[1-2]，区域物流对新型城镇化发展具有带动作用，新型城镇化为区域物流发展创造了新的机遇[3-5]。分析区域物流与新型城镇化的互动关系，是适应区域经济社会高质量发展的内在要求，对实现区域物流与新型城镇化协调发展具有重要意义。

区域物流与新型城镇化发展的互动关系是物流经济学的重要研究领域之一。近年来，国内外学者采用定量方法分析了区域物流与新型城镇化的互动关系。Huffman等[6]利用结构方程模型阐明了物流业发展与城镇化率的关联效应与协调发展机制。李茜[7]基于2000—2012年省级面板数据，利用回归分析方法分析了物流业发展与城镇化率之间的关联性。徐春祥等[8]、刘刚等[9]分别以辽宁和湖北物流业和城镇化发展数据为基础，构建区域物流与新型城镇化协调度评价模型，实证分析了区域物流与新型城镇化的协调性。梁雯等[10]利用1994—2014年安徽省的数据，实证分析了新型城镇化对物流业的影响。邹筱等[11]从互动演进耦合发展关系的角度出发，分析了物流业与新型城镇化的耦合发展关系。梁雯等[12]选取2005—2016年长江经济带9省2市的面板数据，从时空维度分析了物流与新型城镇化的协同发展对新型城镇化的影响。吴垚等[13]、陆欢等[14]利用耦合协调度模型定量分析了物流业与新型城镇化发展的耦合协调关。梁雯等[15]基于灰色关联耦合模型测算了物流产业集聚和新型城镇化发展的关联度及耦合度。朱雁春等[16]基于2000—2015年东部12个省份的数据，分析了物流业与新城镇化耦合协调性的时空演变特性。

总体而言，目前区域物流与新型城镇化关系研究已取得一定成果，但二者的双向互动作用研究尚且不足。因此，本研究考虑区域物流与新型城镇化协调发展的实际需求，构建区域物流与新型城镇化发展的综合评价指标体系，基于2006—2017年黑龙江省区域物流与新型城镇化发展数据，测度区域物流与新型城镇化发展水平，分析区域物流与新型城镇化发展的互动关系。

1 测度指标体系构建

根据系统性、科学性、可衡量性和数据可获取性等原则，结合区域物流与新型城镇发展数据特征，构建区域物流与新型城镇化发展水平测度指标体系[17-19]。其中，区域物流子系统由反映物流能力、发展规模和需求状况的8个指标构成，新型城镇化子系统由反映经济城镇化、人口城镇化、社会城镇化和生态城镇化的9个指标构成。具体情况见表1。

2 研究方法

2.1 发展水平测度方法

熵权法利用指标原始数据的变异程度进行赋权，具有一定程度的客观性。因此，本研究利用熵权法确定区域物流与新型城镇化发展水平测度指标体系各个指标权重，利用熵值-加权综合评价模型来测度区域物流与新型城镇化发展水平。具体计算过程如下：

(1)数据标准化处理

评价指标的量纲及数量级不同，需对各指标进行标准化处理以便对比分析。标准化的计算公式为：

(1)

表1 区域物流与新型城镇化发展水平测度指标体系Tab.1 Measurement indicator system of regional logistics and new urbanization development level

式中，xij为研究单元中i指标j的样本值；max和min分别为研究单元中i指标j的最大值和最小值；标准化后的x′ij取值范围在[0,1]之间。

(2)熵权法

(2)

(3)

(4)

(5)

式中，pij为研究单元i中指标j的归一化值；ej为第j个评价指标的熵值；k和m分别为常数和研究单元总数，二者相关联(k=1/ln(10)=0.434)；dj为第j个评价指标的差异性系数；wj为评价指标的权重。

(3)熵值-加权综合评价模型

在确定各指标权重的基础上，测度区域物流与新型城镇化发展水平，计算公式为：

(6)

(7)

(8)

式中，UL,i为研究单元i的区域物流发展水平；UU,i为研究单元i的新型城镇化发展水平；x′L,ij为区域物流发展水平评价指标的归一化值；x′U,ij为新型城镇化发展水平评价指标的归一化值；wL,j和wU,j分别为区域物流与新型城镇化发展水平测度指标体系中各指标的权重值。

2.2 互动关系测度方法

为揭示区域物流与新型城镇化发展之间的互动关系，利用ADF单位根检验、恩格尔-格兰杰检验、误差修正模型、VAR模型等计量经济学方法，分析区域物流与新型城镇化之间的关系。具体计算公式如下。

(1)ADF单位根检验

ADF单位根检验原假设与备择假设如式(9)所示。

(9)

式中p为统计概率值。

ADF检验一般有3种情形，如式(10)～(12)所示。

(10)

(11)

(12)

式中，Δyt为时间序列yt的一阶差分序列；δ为一阶滞后时间序列的系数；λj为j阶滞后差分序列的系数；j为滞后阶数；ut为白噪声序列；α0为非零常数项；t为时间变量；β0为时间变量系数。

ADF单位根检验的统计量渐近服从ADF分布。若不拒绝原假设H0，则yt为非平稳时间序列；若拒绝原假设，则式(10)～(11)中yt为平稳时间序列，式(12)中yt为趋势平稳序列。

(2)恩格尔-格兰杰检验

恩格尔-格兰杰检验，即对回归方程残差进行单位根检验。如果残差是平稳的，表明变量之间的线性组合平稳，具有协整关系。

如果Xt和Yt均为d阶单整序列，利用最小二乘法估计协整回归：

Yt=α+βXt+ut，

(13)

式中，α为常数项的截距参数；β为在ut不变的情况下，当Xt发生变化时对Yt的影响；ut为误差项或随机干扰项，表示除Xt之外其他影响因素的影响；Xt为解释变量；Yt为被解释变量。

残差et可由式(14)计算得到：

(14)

若et为平稳序列，则Xt和Yt协整，否则不协整。若Xt和Yt不协整，则它们的任一线性组合都是非平稳的。因此，残差et也是非平稳的。

利用ADF单位根检验残差et的平稳性，是针对协整回归计算出的残差项，其ADF临界值比正常的ADF临界值小。

(3)误差修正模型

建立误差修正模型，如式(15)所示：

(15)

式中，c10和c20为常数项；γ11和γ21为修正速度系数；u1t和u2t为随机干扰项；αi(L)(i=1,2)和βi(L)(i=1,2)为方程中变量的系数。

(4)VAR模型

VAR模型的一般表达式为：

yt=Atyt-1+…+Apyt-p+B1xt+…+Byxt-y+εt，

(16)

式中，yt为m维内生变量向量；xt为d维外生变量向量；A1,A2，…,AP和B1,B2，…,BP为待估计的参数矩阵，内生变量和外生变量分别有p和r阶滞后期；εt为随机扰动项。

3 区域物流与新型城镇化发展水平测度

利用2006—2017年黑龙江省区域物流与新型城镇化发展数据，基于熵值-加权综合评价模型测算区域物流与新型城镇化发展水平。涉及的指标数据源自2006—2017年《黑龙江统计年鉴》、《中国区域经济统计年鉴》、《中国城市统计年鉴》、《中国城市发展报告》和《黑龙江省国民经济和社会发展统计公报》。

利用熵权法分别计算区域物流与新型城镇化发展水平测度指标的信息熵、差异性系数及指标权重，结果见表2。

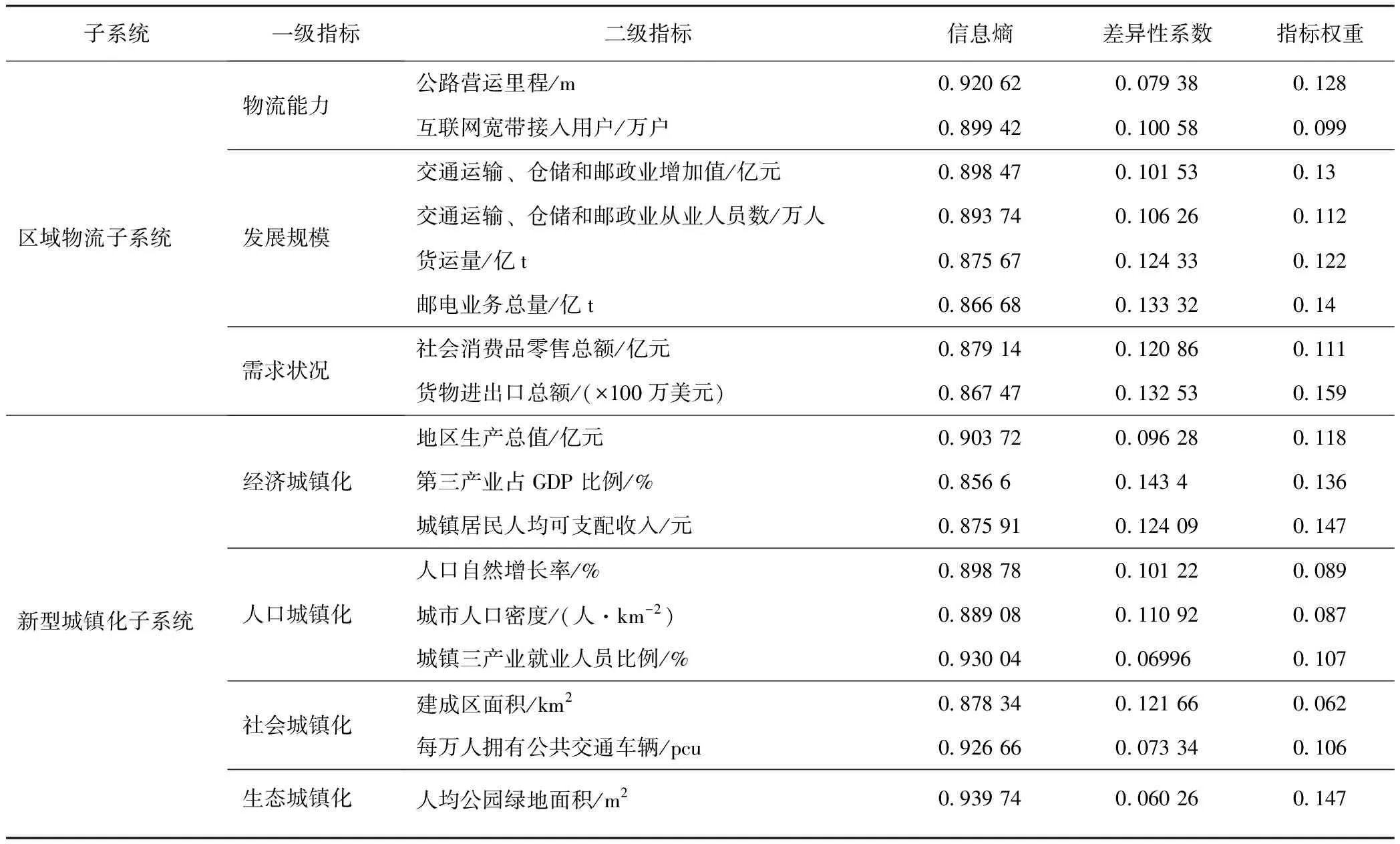
表2 区域物流与新型城镇化发展水平测度指标权重Tab.2 Measurement indicator weights of regional logistics and new urbanization development level

利用熵值-加权综合评价模型，测算2006—2017年黑龙江省区域物流Log与新型城镇化发展水平Urb综合评价值，如图1所示。

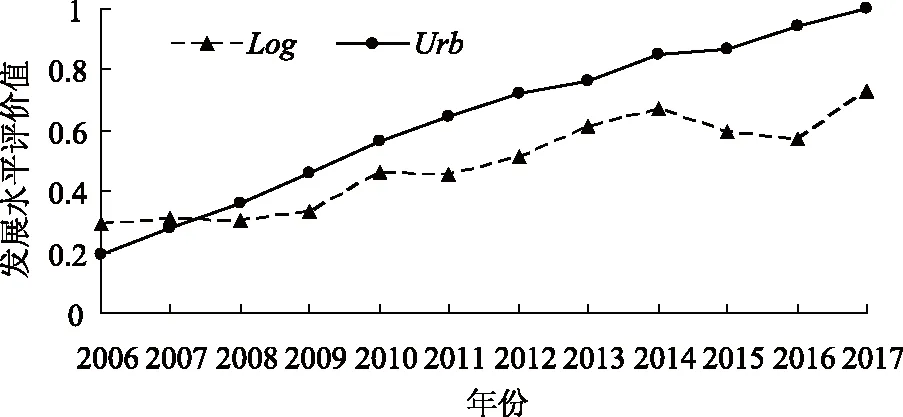
图1 区域物流与新型城镇化发展水平评价值Fig.1 Evaluation values of regional logistics and new urbanization development level

由图1可知，区域物流发展水平综合评价值从2006年的0.293上升到2017年的0.728，新型城镇化发展水平综合评价值从2006年的0.189上升到2017年的0.939，说明黑龙江省区域物流与新型城镇化水平在2006—2017年稳步提升，但二者发展速度并不完全同步。

4 区域物流与新型城镇化互动关系测度

为消除区域物流与新型城镇化发展数据存在的异方差，将其进行自然对数变换。对数处理后的区域物流与新型城镇发展水平评价值及其一阶差分变化情况分别见图2、图3。

图2 区域物流与新型城镇化发展水平评价值对数变化趋势Fig.2 Logarithm trends of regional logistics and new urbanization development level

图3 区域物流与新型城镇化发展水平评价值一阶差分变化趋势Fig.3 First order differential trends of regional logistics and new urbanization development level

4.1 平稳性检验

利用ADF单位根检验法对区域物流与城镇化发展水平时间序列数据进行平稳性检验，结果如表3所示。

表3 区域物流与新型城镇化发展水平时间序列数据ADF检测结果Tab.3 ADF test result of time series data of development level of regional logistics and new urbanization sequence

由表3可知，区域物流与新型城镇化发展水平二阶差分Δ2lnLog和Δ2lnUrb的ADF统计量值分别为-3.259 104和-5.501 658，均小于5%水平下的临界值，表明区域物流与新型城镇化发展是二阶单整序列，满足协整关系检验的前提。

4.2 协整关系检验

利用最小二乘法对区域物流与新型城镇化进行回归分析，得到二者的协整方程：

lnUrb=1.482lnLog-0.158。

(19)

为进一步说明区域物流与新型城镇化之间具有长期稳定的均衡关系，对式(19)进行残差检验，结果见表4所示。

表4 协整方程残差序列的ADF检验结果Tab.4 ADF test results of co-integration regression residual error

由表4可知，在显著性水平α=0.05水平下，协整方程残差序列ADF检验P值为0.011 5，认为该残差序列为不含趋势项与截距项平稳，表明区域物流与新型城镇化存在协整关系。

协整回归模型残差和拟合效果如图4所示。

图4 协整回归模型残差和拟合效果Fig.4 Residual error and fitting effect of co-integration regression model

4.3 误差修正模型

现考察变量短期若偏离均衡如何恢复到均衡状态，即建立误差修正模型。

D(lnUrbt)=-0.002 375+0.574 822D(lnLogt)-

0.650 795D(lnLogt-1)+1.023 184D(lnUrbt-1)-

0.558 464ECM(-1),

(20)

式中，D(lnUrbt-1)为D(lnUrbt)滞后一阶的差分；D(lnLogt-1)为D(lnLogt)滞后一阶的差分；ECM(-1)为滞后一阶的残差。

误差修正模型拟合结果如图5所示。

由图5可以看出，误差修正模型的残差序列基本上是一个零均值的平稳序列，表明模型较好地拟合了新型城镇化序列，可以借助该模型来拟合新型城镇化的变化规律。

图5 误差修正模型的拟合值和残差Fig.5 Fitted values and residual errors of error correction model

4.4 VAR模型

为分析区域物流滞后期对新型城镇化发展的影响，建立VAR模型。当滞后阶数为1时，AIC信息准则达到最小值-5.752 787，而SC信息准则为-5.571 236，见表5。

表5 模型滞后阶数选择Tab.5 Selection of model lag order

因此，可以建立VAR(1)模型，模型结果如表6所示。

表6 VAR模型结果Tab.6 Result of VAR model

由表6可以看出，2个回归模型的拟合度R2分别为0.996 457和0.925 201，表明这2个模型拟合优度高。滞后1期的新型城镇化发展对当期区域物流发展产生正向作用，表明新型城镇化对区域物流发展有较大影响，滞后1期的新型城镇化可促进当期的新型城镇化发展，同时也可促进当期区域物流发展水平提升。而区域物流的滞后期对当前新型城镇化发展没有显著影响，表明上期新型城镇化发展在促进当期的新型城镇化发展增长时，可以提升区域物流发展水平。

lnLog对lnUrb的外生性检验结果如表7所示。

表7 外生性检验结果Tab.7 Exogenous test result

表7外生性检验结果表明, 解释变量lnLog的滞后值对被解释变量lnUrb有显著影响，故模型成立。

5 结论

本研究在构建区域物流与新型城镇化发展水平测度指标体系的基础上，利用熵权法测度了黑龙江省区域物流与新型城镇化发展水平，利用计量经济学方法实证分析了黑龙江省区域物流与新型城镇化发展之间的互动关系，得出如下结论：

(1)熵权法测算结果显示，黑龙江省区域物流与新型城镇化发展水平在2006—2017年稳步提升，但二者发展速度不完全同步，区域物流滞后于新型城镇化发展，二者处于不协调阶段。

(2)平稳性和协整关系检验结果表明，黑龙江省区域物流与新型城镇化发展是二阶单整序列，并表现出一种长期稳定的均衡关系，区域物流对新型城镇化发展具有极大的促进作用。

(3)误差修正模型和VAR模型拟合效果好，可以借助误差修正模型拟合新型城镇化的变化规律，新型城镇化的滞后期对区域物流发展有很大影响。