基于主成分-逐步回归的大跨弯连续刚构桥冲击系数计算
韩智强,左新黛,周勇军,刘世忠,晋民杰
(1. 太原科技大学 交通与物流学院,山西 太原 030024;2. 交通运输部公路科学研究院,北京 100088;3. 长安大学 公路大型结构安全教育部工程研究中心,陕西 西安 710064)
0 引言
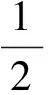
1 冲击系数计算方法
1.1 理论法
车辆荷载作用桥梁结构产生动态响应[9],为简化计算,通常采用冲击系数加以分析:
μ=1-Ydmax/Yjmax,
(1)
式中,Ydmax为车辆过桥时,桥梁动态响应的最大值;Yjmax为桥梁对应位置的静力效应最大。

图1 移动荷载下桥梁冲击系数计算示意图Fig.1 Schematic diagram of bridge impact coefficient under moving loads
1.2 规范法
中国公路桥涵通用规范[10](JTG D60—2015):冲击系数与结构基频f的函数表达式为:

(2)
式中f为桥梁结构的基频。
2 车桥耦合振动基本理论
2.1 车-桥耦合基本假定[11]
(1)桥梁的结构刚度和质量特性应均匀分配桥跨长度范围内。
(2)忽略梁横截面的变形。
(3)桥梁的阻尼采用瑞利阻尼。
2.2 车辆振动方程建立
本研究采用3轴5自由度平面车辆模型,其计算图示如图2所示。

图2 3轴5自由度车辆模型示意图Fig.2 Schematic diagram of 3-axle 5-DOF vehicle model
图中,Mc为车体质量;z为车辆竖向位移;α为车辆横轴旋转的自由度;m1,m2,m3为车辆悬架和车轮等效质量;z1,z2,z3为车辆悬架和车轮等效质量的竖向位移;z′1,z′2,z′3为支承车体点的竖向位移。
车辆的待求未知位移向量为:
ZV=[z1z2z3z′1z′2z′3]。
(2)
i=1,2,3。
(3)
由几何关系可得:
Z=β3z′1+(β2+β1)z′3,
z′2=(β2+β3)z′1+β1z′3,
α=(z′3-z′1)/lu。
(4)
由广义虚功原理得:
(5)
将公式(3)、(4)代入公式(5),整理后,如式(6)所示:
(6)
式中,[Mv]为车体质量矩阵;[Cv]为车体阻尼矩阵;[Kv]为车体刚度矩阵;{Fbv}为车桥耦合荷载向量;{Gv}为重力荷载向量。


(7)
2.3 桥梁动力平衡方程建立
同理,可建立桥梁结构动力平衡方程:
(8)

2.4 桥面不平整度
桥面不平整度,又称桥面粗糙度,表征桥面恶化程度的指标。在实际工程中,由于桥面不平整度的影响,使得车桥振动较为明显,过大的振动会降低乘车人舒适性。因此,在进行车桥耦合分析时,应考虑该因素的影响。本研究根据三角级数叠加法[12]进行模拟,其公式如(9)所示:
(9)
式中,R(x)为桥面不平整度样本点;N为采样频段数;θk为服从[0,2π]均匀分布的随机相位角;S(Ωk)为功率谱密度函数;Ωk为车辆空间频率;ΔΩ-Ωk为间隔带宽[14];
通过调研,我国桥面不平整度大部分处于A~C级,因此,本研究模拟生成3种桥面不平整度曲线,如图3所示。

图3 A,B和C级桥面不平整度曲线Fig.3 Curves of deck roughness of level A, level B and level C
2.5 结构动力响应求解
基于分离迭代法原理,采用Matlab编译车桥耦合分析模块,实现车辆过桥振动响应分析。
2.5.1 位移联系方程建立
假设车轮在运动时始终与桥面保持接触,则车轮位移可通过桥梁的相对位移表示[13],如图4所示:
Δyi=yi-wi-ri,
(10)
式中,yi为轮胎由平衡位置对应竖向位移;ri为车轮作用点处的不平整度竖向坐标;wi为轮胎作用下桥梁瞬时竖向变位;Δyi为车辆轴悬挂弹簧与轮胎竖向变形的相对竖向位移。
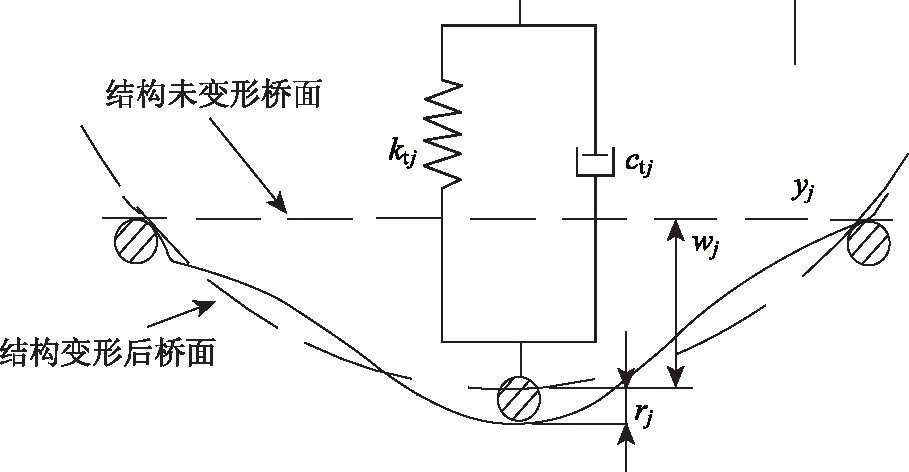
图4 轮桥接触点的位移关系Fig.4 Displacement relation at wheel-bridge contact position
2.5.2 车桥相互作用
将车辆和桥梁视作两个分离体系,二者之间耦合作用通过轮胎与桥面间的相互作用联系。其相互作用力为:
(11)
式中,kti为第i个轮胎的刚度系数;ctj为第i个轮胎的阻尼系数。
3 主成分-逐步回归基本原理
3.1 主成分分析
在大跨连续刚构桥动力特性的敏感参数分析时,由于车桥耦合作用受多种因素的共同作用,在计算分析时,如果采用较多参数进行分析,会使得计算过程较为繁琐,且变量间的多重相关性会影响估计结果,造成模型的误差增大。
主成分分析将多指标参数进行降维处理[14],采用几个变量来替代多个变量的统计方法。
(1)主成分标准化
在对建立模型进行主成分分析时,考虑多个变量间存在不同数量级和单位,在进行相互比较时,为消除量纲对计算模型的影响,需要提前对相关变量进行标准化变换。
(12)

经标准化后的样本矩阵均为无量纲矩阵,且每个列向量的均值为0,标准差为1。
(2)求解特征值λi和特征向量ej
特征方程通常采用雅可比法(Jacobi)求解特征值λi,并根据特征值的大小进行排列,其中当λ1≥λ2≥…≥λp>0时,相应正则化特征向量为:
ej=|l1jl2j…lpj|′,j=1, 2,…,p。
(13)
(3)主成分方差贡献率的确定
在实际工程中,主要通过方差贡献率的累积量确定主成分的个数。其中λi的方差贡献率可通过式(14)求解。
(14)
式中,αi为代表第i个因素的方差贡献率;α(m)为前m个因素的方差累计贡献率。
由式(14)可知:主成分的方差贡献率越大,表明该主成分保留因变量的信息能力越强,如果前m(m≤p)个主成分的累计值达到一定数值(本研究取方差累计贡献率Ti≥90%),表明这m个主成分涵盖了样本的绝大部分信息,则这m个主成分可作为因变量分析的主要敏感参数。
3.2 逐步回归分析
当冲击系数受m个因素影响时,可通过多元线性方程来描述,其关系式为:
(15)
逐步回归[15]是一种双向筛选法,其本质属于前进法,即变量从少到多引入时,采用最小二乘法建立多元回规方程,基于偏回归平方和F检验,判断方程是否显著,剔除其中不显著的影响因素,其主要步骤如下:
(1)对主成分分析中的相关自变量进行回归分析,分别计算因变量与自变量间样本点的拟合度R2。
(2)对各个自变量所对应的R2进行排序。
(3)选取最大值R2变量Ai建立回归模型,计算R1,F1。
(4)选取排序第二R2的变量Aj的回归模型,计算R2,F2。
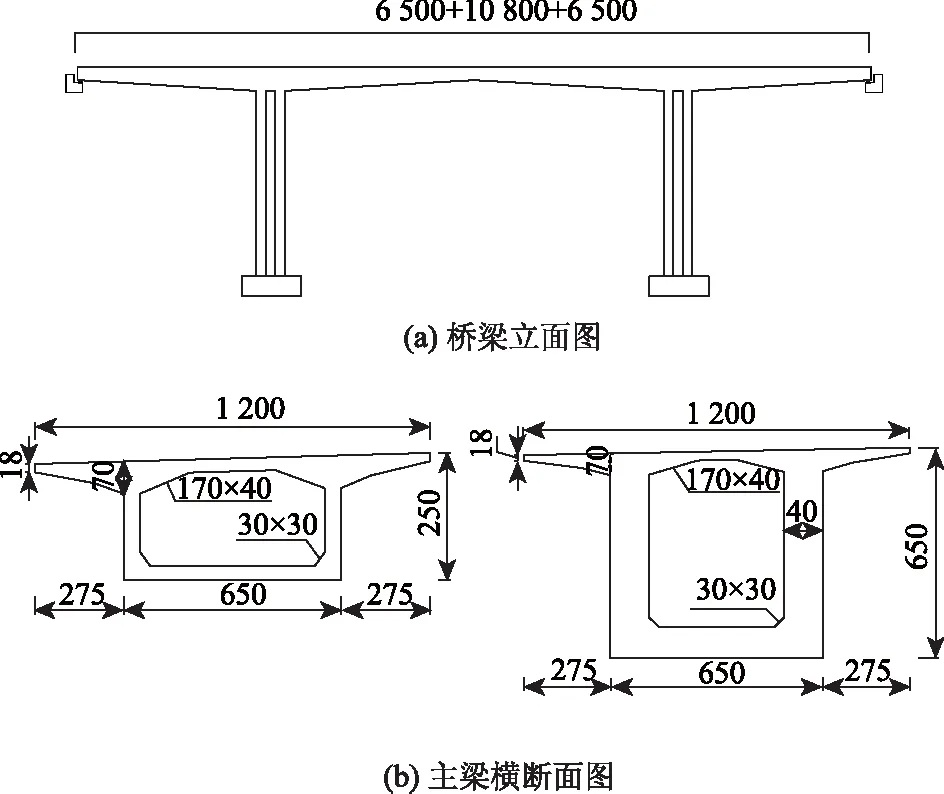
若R1 (5)重复步骤(4),进行下一个变量筛选,直到所有主成分变量都筛选后,结束计算。 图5 技术路线图Fig.5 Technology route 本研究以某高墩大跨连续弯刚构桥为工程背景,桥梁全长239 m,跨径组合 (65+108+65) m,上部结构采用单箱单室截面,曲率半径R=960 m,下部结构采用薄壁空心墩,墩高60 m,主梁采用C50混凝土,桥墩采用C40混凝土[11],其相关尺寸和仿真模型如图6~7所示。 图6 连续刚构桥总体布置(单位:cm)Fig.6 General arrangement continuous rigid frame bridge (unit:cm) 图7 桥梁仿真示意图(单位:cm)Fig.7 Schematic diagram of bridge simulation(unit:cm) 根据相关学者的研究[16-17],本研究选取了桥面不平整度、曲率半径、桥墩高度、行车速度、车辆重量作为大跨弯连续刚构桥车桥耦合分析的敏感参数。为简化计算,本研究对5个敏感参数进行主成份分析,确定其相对重要的敏感参数,见表1。 表1 车桥耦合敏感参数影响因素Tab.1 Influencing factors of vehicle-bridge coupling sensitive parameters 在敏感参数降维分析时,采用德尔菲法对敏感参数进行评估,具体步骤如下: (1) 确定调研主旨和目的,设计敏感参数调查问卷。 (2) 选取在车桥耦合方面有较为丰富科研或工程经验的专家。 (3) 发放调查问卷,并与专家建立函询工作,搜集相关结果。 (4) 对结果进行统计汇总,并将计算结果进行主成分降维分析。 (5) 搜集原始资料 按照敏感因素对车桥耦合冲击系数的影响程度划分10个等级,使用0~10进行评分,见表2所示。 表2 影响因素评分划分Tab.2 Score division of influencing factors 向上述专家进行问卷调查共计40人,回收筛选出有效样本36份,进一步整理数据,得到待评价矩阵{Aij}n×k,其中k为评价因素,即k=5,n为有效样本。 采用SPSS22.0进行数据处理,得到相关系数矩阵R特性值,方差贡献率和累计方程贡献率,如表3所示。 表3 R的特征值、方差贡献率、累计方差贡献率Tab.3 Eigenvalues, variance contribution rates and cumulative variance contribution rates of R 通过表3可知,特征值大于1的主成分个数g=3,此时方差累计贡献率为95.852%,超过了主成分分析的90%,即涵盖了大部分信息,这表明前3个指标能代表5个指标来分析大跨弯连续刚构桥冲击系数变化情况,通过文献[18]可知,车速对于桥梁位移、弯矩和扭矩冲击系数的影响幅度不大,验证了降维方法的正确性,因此,本研究后续对前3个指标进行敏感性分析。 大跨弯连续刚构桥冲击系数受多个敏感参数共同作用。本研究通过拟定,曲率半径取值为250,500,750和960 m;墩高取值为60,80和100 m;路面不平整度等级取值为A, B和C级。求解桥梁关键截面的挠度、弯矩、扭矩的时程曲线,如图8所示,其中车辆的基本参数如表4所示。 图8 桥梁关键截面时程曲线Fig.8 Time-history curves of key sections of bridge 通过公式(1)计算各个关键截面处挠度、弯矩和扭矩冲击系数,从中找出挠度,弯矩和扭矩冲击系数最大值,如图9所示。 通过采用SPSS22.0对图9中相关数据进行线性逐步回归分析,得出各个敏感参数对冲击系数的贡 表4 车辆技术参数 [19]Tab.4 Technical parameters of vehicles 图9 大跨连续刚构桥最不利截面冲击系数最大值Fig.9 Maximum impact coefficient of key section 献性大小,结果如表5所示。 由表5可知: (1)检验回归系数全部为0,小于sig显著性分析界限值0.05,表明自变量参数与因变量参数的线性相关性较好,模型1挠度冲击系数分析时,主要取边跨跨中截面和中跨跨中截面处挠度冲击系数的最大值作为因变量,其因变量受桥面不平整度、墩高的影响性较为显著,而曲率半径对其影响相对较小,可忽略该因素的影响;模型2弯矩冲击系数主要考虑跨中截面正弯矩和支点负弯矩的最大值作为因变量,其值受桥面不平整度的影响较为显著,墩高和曲率半径对其影响相对较小,可忽略不计;模型3扭矩冲击系数分析时,其因变量受桥面不平整 表5 系数分析表[12]Tab.5 Coefficient analysis table 度和曲率半径的影响较大,而墩高影响较小,可忽略不计。 (2)挠度、弯矩和扭矩冲击系数的回归公式相关系数R均在0.94以上,表明该回归公式相关性较好;且各回归公式均与桥面不平整度正相关,其标准化相关系数Beta均在0.9以上,表明该因素对大跨弯连续刚构桥冲击系数的影响很大,而现有规范未考虑该因素的影响,建议后续规范修订中考虑该因素的影响。 (1)采用ANSYS软件建立桥梁模型,通过Matlab软件编译车桥耦合分析模块,基于位移协调方程构建车桥耦合分析模型。 (2)采用主成分-逐步回归分析方法去确定桥面不平整度、曲率半径和墩高作为桥梁冲击系数分析的主要敏感参数,其方差累计贡献率达到95%,并通过SPSS22.0进行逐步回归,确定了桥梁挠度、弯矩和扭矩冲击系数的计算公式。 (3)冲击系数回归公式相关系数R均在0.94以上,表明该回归公式相关性较好,且各个公式中桥面不平整度标准化相关系数Beta均在0.9以上,表明该因素对大跨弯连续刚构桥冲击系数的影响很大,而现有规范未考虑该因素的影响,建议后续规范修订中考虑该因素的影响。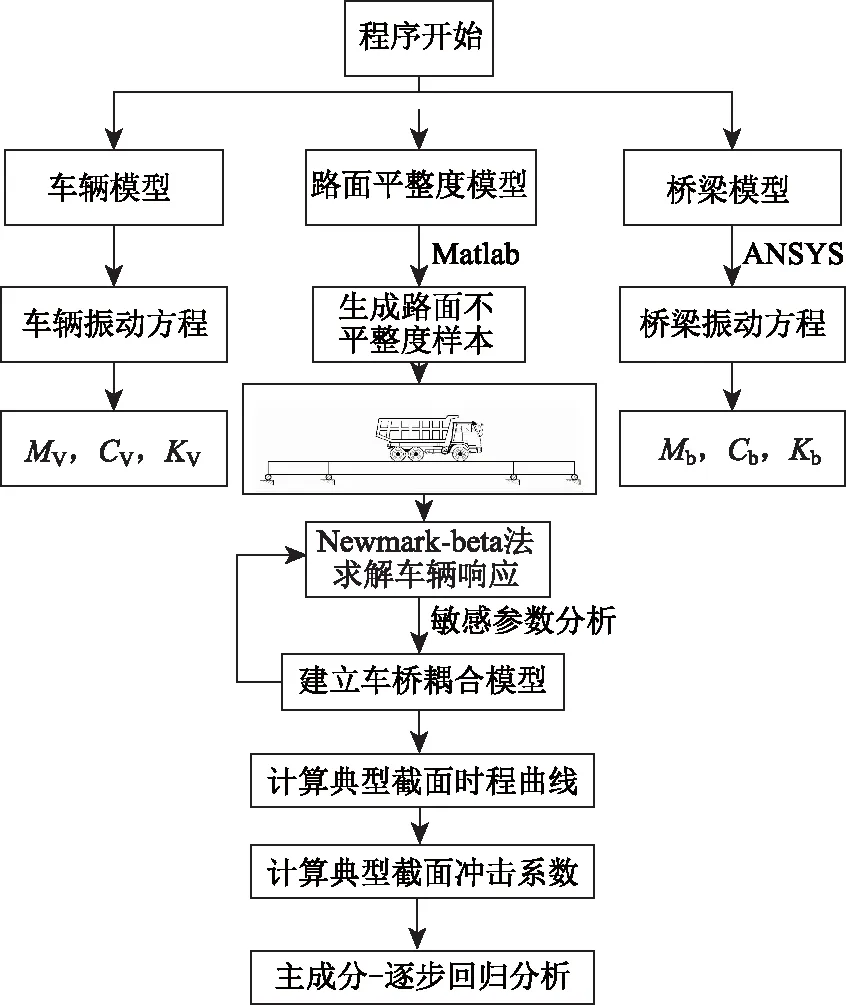
4 敏感参数下大跨弯连续刚构桥冲击系数分析
4.1 工程简介
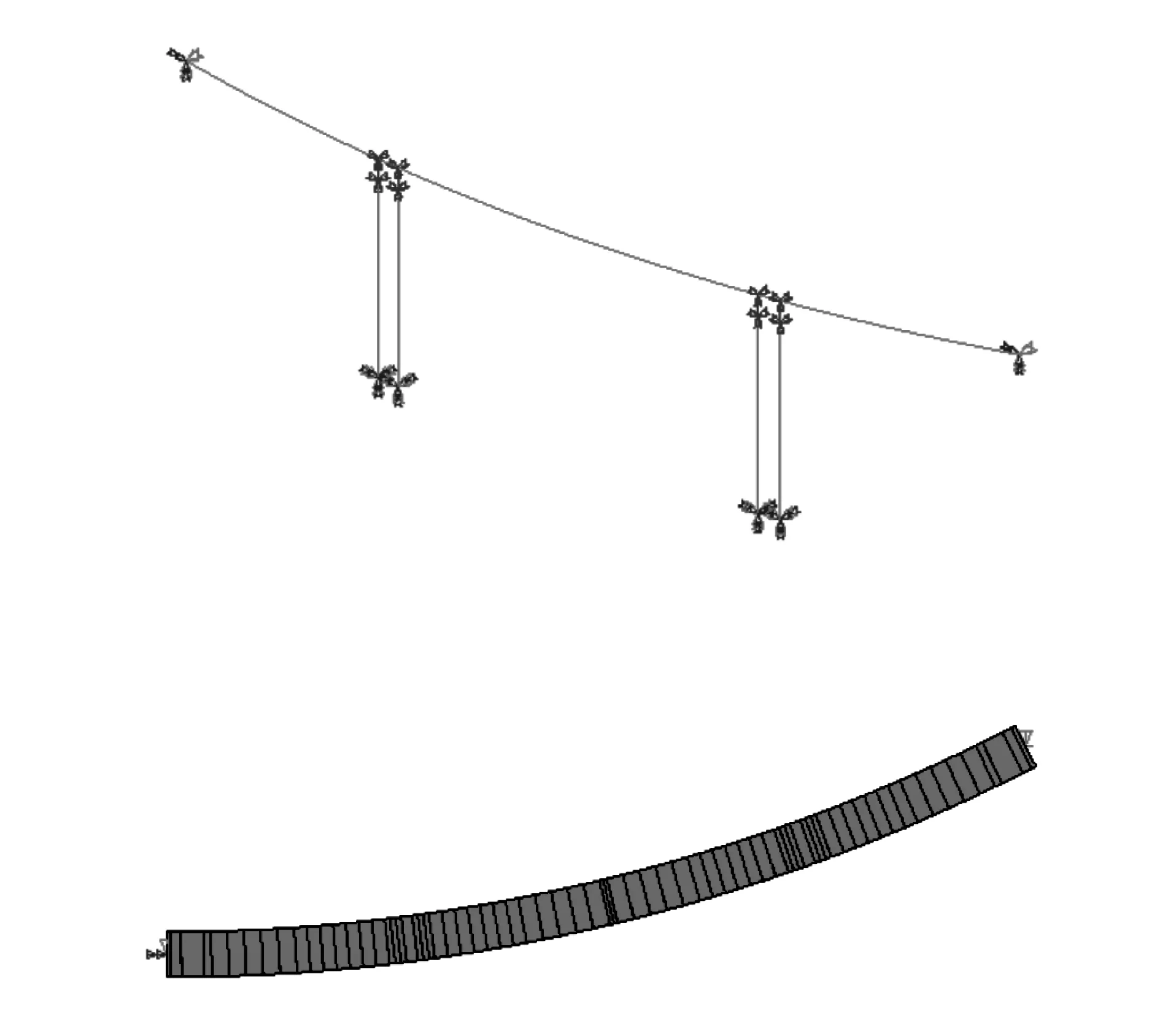
4.2 敏感参数主成分分析

4.2.1 敏感参数降维分析

4.2.2 敏感参数主成分分析

4.3 敏感参数下桥梁动力时程曲线

4.4 大跨弯连续刚构桥冲击系数回归分析4.4.1 关键截面冲击系数最大值确定
4.4.2 桥梁冲击系数回归分析



5 结论

