基于离散元仿真中堆积角评定新方法

刘 珂 魏伟锋，2*

（1、陕西理工大学机械工程学院，陕西 汉中 723000 2、陕西省工业自动化重点实验室，陕西 汉中 723000）

散体颗粒广泛存在于自然界中，可作为加工对象或相关装备的承载介质[1]，散体颗粒特性研究对采矿、冶金、食品、能源、化工及农业等领域的装备开发具有重要意义[2]。堆积角是散体颗粒特性参数之一[3]，是颗粒物筛分、输送、存储装备开发的基础参数之一。

传统的堆积角通过堆积实验法得到，方法1：人工用角度仪对堆积体的几个截面进行测量和数据处理得到堆积角度，具有直观简便的特点；方法2：通过不同角度堆积照片，对图像处理得到堆积角。其共同点在于：测量对象是三维实体，测量截面的选择对测量结果具有一定的影响，无法全面利用堆积体的几何信息。

离散元仿真软件的发展为散体颗粒的研究提供了新途径。相关研究表明：a.在离散元仿真中可以将不规则的物体用相对规则的物体近似代替[4]；b.离散元模型的填充颗粒半径越小仿真结果越接近真实值[5]；c.动摩擦因数及静摩擦因数等物料参数的设置对仿真的结果具有重要的影响[6]。

离散元模型参数通常难以通过试验测的，为获取离散元仿真参数，研究者需要进行相应的模型参数标定；离散元模型的表征参数，一般通过堆积试验与仿真结果对比进行离散元模型表征参数标定；基于离散元堆积角测量目前主要通过两种方法。方法1，直接采用仿真软件中的角度测量工具人为绘制边界，如文献[7-10]，该方法容易引起人为误差；方法2，通过图像处理得到堆积角，如文献[11-14]在标定不同离散元模型参数时，先将堆积体转化为图片，然后对其二值化的边界采用最小二乘法得到堆积角。以上处理方法的共同特点在于：以堆积体上的有限截面作为样本，未能充分利用堆积体的三维轮廓信息，造成降维性原理误差。

为充分利用离散元仿真结果的三维数据，来提高堆积角的计算精度和效率，本文以粳米为例，建立离散元模型，模拟粳米自然堆积过程，得到每粒粳米颗粒的质心坐标，采用一种处理方法，提取三维质心堆积体表面质心点集，将表面质心点集绕轴线旋转至同一象限，进行线性拟合，获得堆积角度。

1 堆积角离散元仿真

1.1 颗粒模型

假设粳米颗粒为椭球体，其长轴为6.2mm，短轴为2.8mm[15]，通过三维制图软件绘制三维模型并保存，三维模型导入到离散元仿真软件中，得到的颗粒模型轮廓如图1 所示。

图1 粳米离散元模型

1.2 颗粒模型堆积条件及边界参数

在离散元仿真软件中，需对钢筒中填充颗粒数估算，按照公式（1）对其估算[16]，便于设置颗粒生成数量，颗粒、无底钢筒之间的边界参数如表1 所示。

表1 接触模型参数

式中，α 为填充体积分数，α 一般取值为0.56；Vs为无底钢筒体积（mm3），N 为填充颗粒数量（个），VF为填充颗粒的体积（mm3）。

1.3 离散颗粒堆积仿真过程

将半径为30mm，高为180mm 的钢筒及200mm×200mm 的不锈钢底面三维模型导入离散元仿真软件中，钢筒填充满粳米颗粒，设置钢筒以0.05m/s 的速度向上移动，当离散模型堆积形状不再发生改变后仿真结束，粳米将在底面上形成一个近似的锥体，其过程如图2 所示。改变颗粒的填充效果，重复上述过程，获得一组堆积角仿真数据。

图2 离散颗粒离散元仿真过程

2 堆积角评估方法

为了充分利用离散元仿真得到的堆积体三维信息，更为全面的反映堆积角，提出如下方法。

2.1 三维数据预处理

将离散元仿真结果的颗粒质心坐标导出，通过式（2）计算三维锥体质心坐标，由式（3）计算出，颗粒质心距三维锥体质心坐标距离，过质心坐标垂直于地面的直线为轴线。以轴线为三维堆积体坐标系Z 轴，形成堆积体坐标系，如图3 所示。

图3 三维质心及轴线

式中，n 为颗粒数量（个），xc、yc、zc为三维锥体质心坐标（mm），xi、yi、zi为颗粒质心坐标（mm）。

式中，xr、yr为堆积角坐标系中颗粒相对横坐标、纵坐标（mm）。

2.2 三维边界法

在Matlab 中，首先将堆积时，散落在堆积体外部与堆积体底部颗粒剔除，再通过boundary 函数将堆积体边界点集提取，并获得边界点集包络图，如图4 所示。

图4 堆积体边界

将堆积体边界点集以堆积体坐标系Z 轴为旋转中心，旋转至同一象限，得到堆积体边界点集图，对其采用最小二乘法进行线性拟合得到拟合直线，拟合方程形式：y=-ax+b。拟合图像如图5 所示。

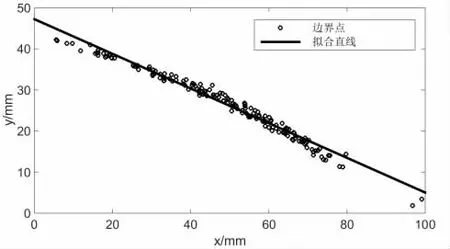
图5 边界点线性拟合

3 堆积角试验对比

3.1 试验准备

为保证试验与离散元仿真软件的条件相同，在试验前对粳米进行挑选，对破损、形状过小及过大的粳米进行剔除；无底钢筒取半径为30mm，高为180mm 的无底钢筒，将筛选后粳米填满无底钢筒备用。

3.2 堆积试验

将装满粳米的无底钢筒，放置在不锈钢试验台上，以0.05m/s 的提升速度在试验台上进行试验，实际堆积体如图6所示。

图6 实际堆积体

3.3 结果与分析

对图6 分四个方向进行图像二值化处理，提取边缘获得轮廓线，进一步对轮廓线进行线性拟合，图像处理结果如图7 所示。计算堆积角公式（6），对计算结果取平均值，如表2所示。

表2 实际试验堆积角

图7 (a) 二值图像(b) 线性拟合

式中，θp为实测堆积角（°），h 为粳米的堆积高度（mm），r 为粳米的堆积半径（mm）。

以图像法得到的实际堆积角为基准，使用公式（5）计算相对误差，结果见表3。

表3 堆积角相对误差

式中，δ 为相对误差（%），θs为离散元仿真堆积角度（°），θp为实测堆积角（°）。

由表3 可知，本文测量方法与实际堆积实验误差为1.6%，在5%以内，是一种可靠的测量离散元仿真三维堆积角的新方法。

4 结论

4.1 基于离散元法仿真得到颗粒质心三维数据，通过计算堆积体质心，提出两种边界提取途径，采用最小二乘法拟合边界得到堆积角，充分利用堆积体边界数据，实测堆积角与本文方法对比表明：相对误差在5%以内，绝对误差在±2°以内，表明本文提出通过三维堆积体质心边界计算堆积角的可靠性。

4.2 本文提出的方法，克服了相位选择和测量方向对堆积角计算和测量的影响，为离散元仿真评估堆积角提供了一种新的方法和思路。