基于ZEMAX 的板条激光器光束准直系统的设计

林德清 赵 爽

（北京信息科技大学 仪器科学与光电工程学院 光电信息科学与工程专业，北京 100192）

1 概述

因为具有高速调制性，高集成度，高可利用率和高可用度，高密度信息记录，激光测量，激光打印，激光雷达，激光制导和读取等领域广泛使用了固态激光器这一工具[1-4]。然而传统的激光器热效应很高，这大大影响激光器的输出功率和光束质量。1972 年，琼斯巧妙地利用了板条状几何对称和大散热面积的优点，提出将固态激光器的增益介质设计成板条状结构。该结构可有效的减少热效应，而且由于激光介质厚度上非常薄，加之在晶体的大面上可大幅散热，光学畸变也会由此变小。因此，传统激光器因为无法解决热效应问题常常与板条激光器在应用场景的比试中落败[5]。然而板条激光器的垂直发散角和平行发散角在这两个方向上有差异，且输出光束的光斑和固有像散也成不规则形状，使得板条激光器在远距离测距等应用上的精度受到了极大的影响，光束必须准直。

2 理论分析

2.1 子午方向

如图1 所示，建立子午方向的准直系统的四象限坐标系系，半导体的激光光束从R 点发射，直线到达柱面透镜M1的平面一侧并发生第一次折射，光线在透镜内传播后在弧面处发生第二次折射并射出透镜。计其半发散角为α，第一次折射点为M，第一次折射角为φ，第二折射点为N，第二次折射的折射角为Ф，且第二折射点处的法线与x 轴之间角度为θ，射出的准平行光束的半分角为θ1/2//。

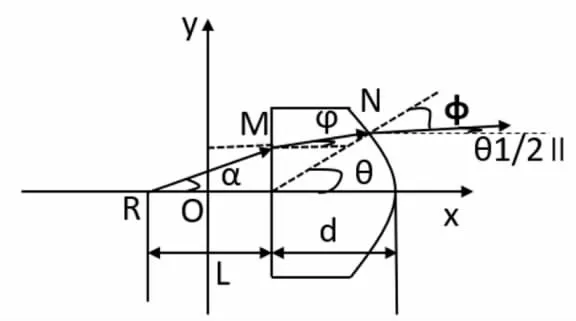
图1 准直系统子午方向光路图

图1 中，设椭圆弧线的方程为：

已知R 为激光的发射原点，且椭圆的中心点为点O，所以根据光束的折射定律得:

直线MN 的方程为:

已知N 点满足椭圆的解析式，且N 点落在椭圆曲线上，椭圆的方程式为：

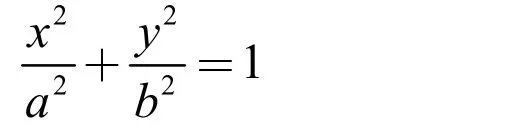
联立上述椭圆方程和方程（4）可求得此处N 点的坐标:

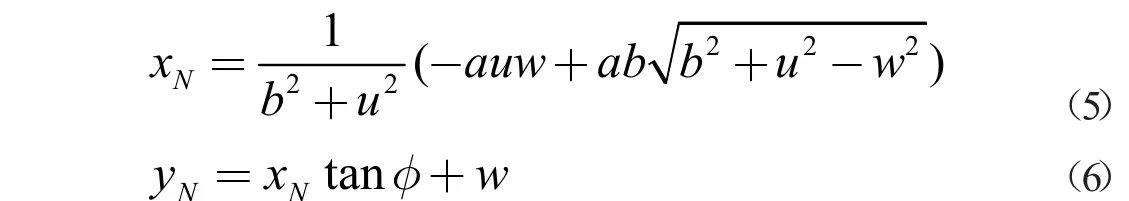
上面两式均为简化结果，式中u=atan ϕ,w=Ltanα- (a-b) tan ϕ

N 点处的椭圆弧的切线斜率为：

又因为kk'=-1 且已知第二次折射点N 处法线的斜率为k= tanθ，因此得:

此时联立上述方程组由（3）式可得：

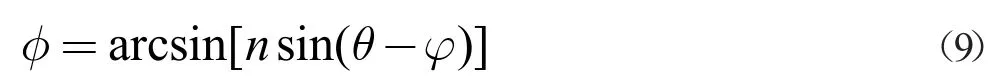
由（2）式可得：

联立以上的方程组，最后计算得到垂直方向的发散半角为：

2.2 弧矢方向

如图2 所示，在弧矢方向上的分析和计算方法和在垂直方向上的基本保持一样。

图2 准直系统弧矢方向光路图

根据几何光学的知识可知，平行方向的激光光束在经过第一个柱透镜M1 并发生第一次折射时其发散角并没有发生任何改变，由图可知，点R' 为折射光的反向延长线交点，如果将它看作此方向上激光束的发射远点，激光束发射点与柱面透镜M2的距离则可表示为：

在公式（12）中，L 是光源与透镜M1 的距离，As 表示半导体激光器的固有像散，数据显示固有像散约为几微米，∆表示激光束在平行方向通过第一个柱透镜时的向前偏移量，d 是第一面透镜的厚度，e 是两个透镜M1 和M2 之间的距离。可以通过调节As 和∆消除像散并减少计算和分析的难度和误差。有了以上的数据后，通过将L'和d'的值和子午光线的方程联立可以计算出弧矢方向的发散角。

2.3 仿真设计

整个系统的数值模拟通过上面计算的发散角公式进行。为了降低设计的复杂性，有必要尽早确定一些可选参数，即玻璃材料。型号为H-K9L 的玻璃因为便于加工被选为这次仿真的柱面透镜材料，H-K9L 玻璃的折射率是n=1.5163。椭圆柱面镜的初始结构可由H-K9L 的折射率与发散角公式联立算出: 在垂直方向上，取L=1.5mm，a=12mm，b=5mm，n=1.5163，d=4mm，计算结果表明，0.0029rad 为此次半发散角在垂直方向上被压缩的最终数值; 在平行方向上，取L'=6.5 mm，a=32.5mm，b=12.5mm，n=1.5163，d'=4mm，0.0020rad 为此次半发散角在平行方向上被压缩的最终数值。上述计算出的标准参数将作为后续ZEMAX 仿真中柱面透镜的初始数据。

在ZEMAX 中标准面面型公式为：

在上式中，c 是曲率（1/R），r 是柱面镜表面近轴部分的曲率半径，k 是二次曲面常量，用于确定柱面镜中面的类型，当—1＜k＜0 时，曲面为横椭圆。其中R 和k 的计算方式如下:

在上面的公式中，a 是椭圆柱镜的半长轴，b 为椭圆柱面镜的半短轴，将透镜M1 和透镜M2 的结构数据分别与公式（14）和公式（15）联立可得两面透镜的曲率半径及其二次系数，分别为:R1=—2.083mm，k1=—0.826;R2=—4.808mm，k2=—0.852。

3 ZEMAX 仿真

ZEMAX 是一款广受光学工程师们欢迎的光学设计分析系统。计算出的初始透镜结构数据被输入ZEMAX 的非顺序模式以进行模拟。

首先在非序列模式中输入板条激光器的数据，其中需要注意的几点是：（1）非序列中输入的发散角为发散半角。（2）激光器类型需选择source Diode（固体激光器）类型。（3）为了能在之后设置的探测器上追踪到光束，激光器光束需要设置一定数量的Analysis Rays（可分析光束）。

图3 显示了在ZEMAX 非序列模式中模拟的板条激光器，发散角为θ//=15°和θ⊥=30°，激光总功率为70W。

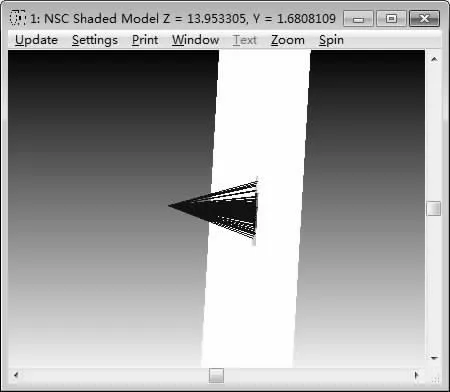
图3 ZEMAX 非序列模式板条激光器模拟结果

基于上述初始结构，进行了相应的优化，因为使用的ZEMAX 软件版本相对较低。所以非序列模式中的优化功能并不健全，因而选择将初始结构转化到序列模式中进行优化。

在优化时选择将两个柱面镜的二次曲面常量、曲率半径、两镜子间的距离和光阑面的位置设为变量，最终的镜头数据如表1 所示，在表1 中，Biconic 代表柱面透镜，z 坐标代表距光源的距离（此时光源设置在建立坐标系的零点以便于计算和分析），透镜材料是H-K9L 玻璃，x 和y 的半宽度表示两个方向上的透镜宽度，R 和k 参数一起确定柱面透镜的面形状为椭圆形表面。两透镜第一面的数据由于是平面所以可以忽略。

表1 最终镜头数据

将优化后的数据输入到非序列模式中进行模拟，在镜片后面添加相应的探测器，选择detector Rect 类型的探测器进行探测，接收面选择50X50mm 的尺寸。需要注意的是需要先在探测器上追踪一定时长内的光斑才能在探测器上分析光斑。在表1 中的最终参数设置下分析激光束的光斑，在模拟器中将光束打到设置的接受表面上可以获取到相应的激光光斑和光场分布。通过光斑和所对应的光场可以分析光斑尺寸。在光场分布图中通过记录光场最外边缘与x 轴交点的横坐标来获取激光束光斑的半径；通过记录与y 轴交点的纵坐标同样可获取此时光斑的半径。在x 方向上分别设置距准直系统5m 和10m 的探测器，分别检测激光束光斑在x 方向上的光场强度分布图，如图4 和图5 所示。光场分布图的水平轴表示坐标信息（单位：Mm），纵轴表示相应横坐标处的激光非相干亮度（单位：W/cm2）。

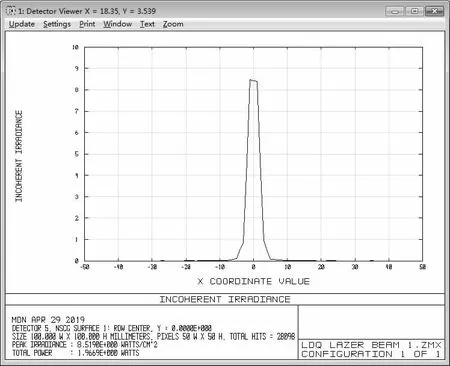
图4 激光束光斑在x 方向5m 上的光场强度分布图

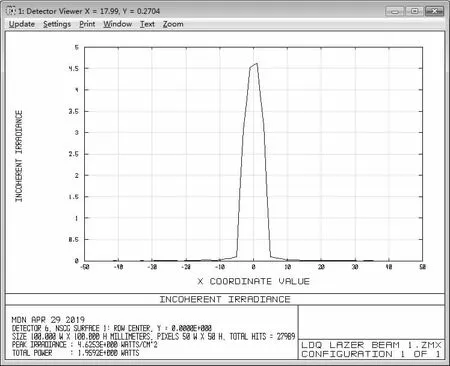
图5 激光束光斑在x 方向10m 上的光场强度分布图

由图4 和图5 所示，在5m 处激光束的光斑半径为Rx1=18mm，在10m 处激光束的光斑半径为Rx2=29mm。将此处所观察到的值代入半发散角公式θ1/2//=(Rx2—Rx1)/(z2—z1)可得此时在x 方向上的半发散角为1.8mrad。

由图6 和图7 可知，在5m 处激光束的光斑半径Ry1=14mm，在10m 处激光束的光斑半径分别Ry2=19mm。将此处所观察到的值代入半发散角公式θ1/2⊥= (Ry2 —Ry1)/(z2—z1)可得此时在y 方向上的半发散角为1.04mrad。观察可知在快轴和慢轴上，激光束的分布与标准高斯曲线基本一致；激光束在子午方向和弧矢方向上的均压缩在半径为7mm 的光斑内，图8 为最终的远程测距效果。

图6 激光束光斑在y 方向5m 上的光场强度分布图

图7 激光束光斑在y 方向10m 上的光场强度分布图

图8 最终的远程测距结果

4 结论

基于ZEMAX 软件和几何光学原理，推导了准直系统准直后激光束发散半角的计算公式并设计及模拟仿真了一个由两个相互垂直的柱透镜组成的板条激光器准直系统。确定初始参数并重复计算以获得准直系统的初始结构数据。然后将该初始数据导入ZEMAX 光学设计软件以评估初始结构的结果。接下来进一步优化初始参数以提供更好的结构。优化后的结果显示，激光光束在通过准直系统后在快轴和慢轴上的发散角分别为3.6mrad 和2.08mrad，达到预期的目标。