基于协同过滤的图书推荐系统

赵宇凤

(宝鸡职业技术学院，教务处,陕西，宝鸡 721013)

0 引言

作为业务创新的重要技术手段，推荐系统被广泛用于向用户推荐最合适的产品、服务或内容[1-2]。在图书馆中也可借助图书推荐系统预测读者潜在的阅读偏好，从而提升读者满意度，提高图书馆的服务水平。推荐系统的核心是使用借阅记录和相应的归还记录来创建与读者、图书相关联的评分矩阵，通过评分的高低向图书馆读者推荐图书。由于图书借阅次数是有限的，评分数据较为匮乏，因此通常该评分矩阵是稀疏的。为了解决稀疏问题，本研究使用矩阵分解方法来处理具有稀疏特征的评分矩阵，提升图书推荐系统的准确性。使用真实借阅记录组成的数据集进行实验，结果表明该图书推荐系统的准确率是可接受的。

1 协同过滤和矩阵分解方法

1.1 协同过滤

协同过滤算法的主要思想是通过使用具有相似偏好和兴趣的其他读者的行为来预测一个指定读者对某种图书是否感兴趣[3-5]。假设有一个m个用户组成的列表U={u1，u2，…，um}和一个n个图书组成的列表I={i1，i2，…，in}。在本研究中，基于协同过滤的预测问题是依据每个读者Ui为图书列表Iui给出的评分，预测出尚未对图书列表评分的读者Ua对指定图书Iua的偏好评分。协同过滤过程如图1所示。

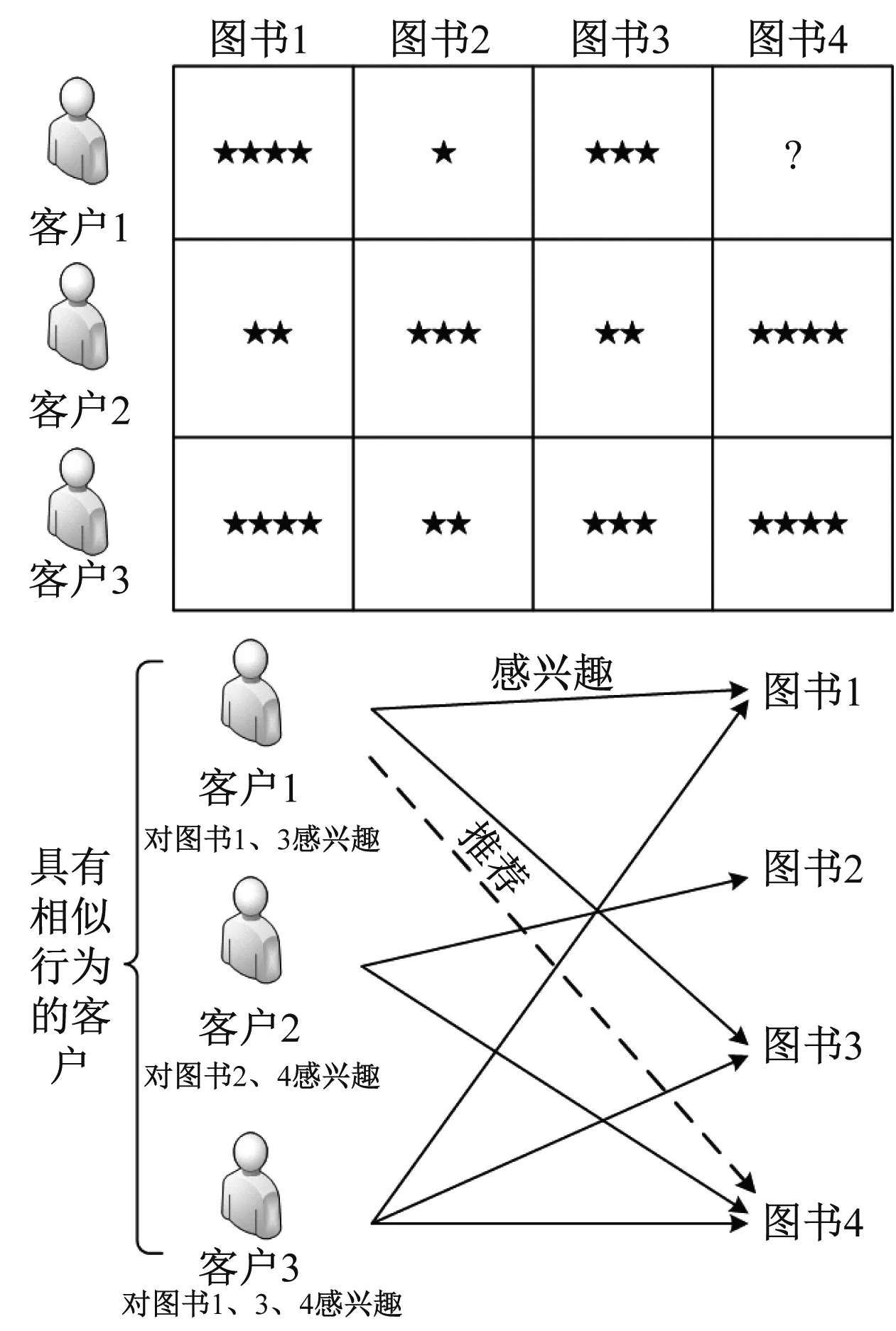
图1 协同过滤的流程

协同推荐技术包括最近邻读者计算和产生推荐列表2个步骤。

(1)最近邻读者计算

最近邻读者是读者之间的相似度计算得出。领域越大，最终的推荐结果也越准确。读者之间相似度的计算方法较多，本研究使用以下3种方法：皮尔逊相关系数法、余弦相似度法和欧式距离法[6]。实验将确定哪种方法最优。

令包括读者u和v的评分矩阵用I表示，则这两个读者之间的皮尔逊相关系数的计算式[7]为式(1)。

(1)

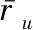
读者u和v之间的余弦相似度sim(u,v)的计算式[8]为式(2),

(2)

两个读者u和v的欧氏距离的计算式[9]为式(3),

(3)

为了便于对比，使用式(4)对计算得出的欧式距离进行归一化转换,

(4)

(2)产生推荐列表

产生推荐列表的依据是图书的偏好得分。图书的偏好得分越高，在推荐列表中排序就越靠前。选择一组与活动用户u(即待预测读者)最近邻的k个读者，并将这k个读者的评分用于预测活动用户u对指定图书i的偏好评分Pu,i。图书偏好得分的计算式为式(5),

(5)

尽管基于相似读者的协同过滤比较容易实现对偏好评分的预测，但是这种方法对数据稀疏性很敏感，而图书评分数据往往比较匮乏，这意味着没有足够的数据可供预测使用。本研究提出矩阵分解模型以解决这个问题。

1.2 矩阵分解

矩阵分解是解决推荐系统中稀疏数据问题的一种技术。矩阵分解模型将读者和图书都映射到维度为f的联合因子空间，以便将读者和图书之间的关联关系建模为该空间上的内部映射关系[10]。每个图书项i与向量qi∈Rf相关联，每个读者u与向量pu∈Rf相关联。其中Rf是f维的实空间。对于给定的第i个图书项，向量qi元素衡量了图书所对应隐特征的被关注程度。对于给定的读者u，向量pu衡量了读者对所对应隐特征的偏好程度。换句话说，矩阵分解的结果是给出与读者和图书的隐特征向量，这2个隐特征向量的点积就是图书对应读者的推荐分数[11]。矩阵分解的计算示例如图2所示。

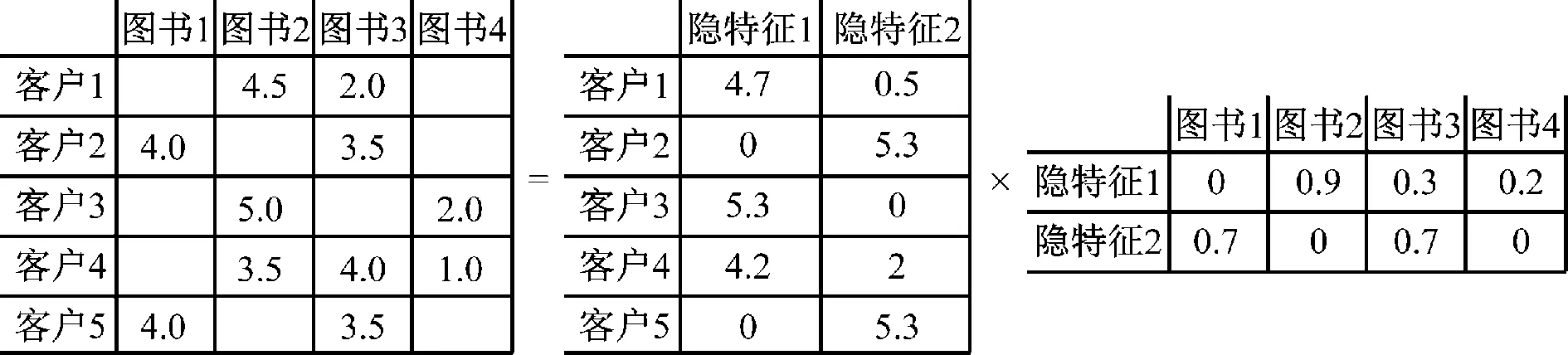
图2 矩阵分解示例

2 研究数据集和推荐方法

2.1 数据集

使用2018—2019年某大学图书馆的41 767名不同专业、年级学生的图书借阅记录作为本研究的数据集。数据集被分为两部分，80%用作训练数据集，剩余20%用作测试数据集。这些图书借阅记录在本研究中被用来生成针对学生的推荐图书。

2.2 推荐方法

本研究所提出的基于协同推荐的图书推荐方法包括以下5个步骤。

步骤一：图书馆借阅记录中有较完整的学生借阅记录,由于缺乏足够的能够说明学生对所借阅图书是否满意的原始评分数据，因此本研究根据借阅记录和相应的归还记录计算学生借阅时间长度，通过借阅时间的不同长度来生成学生对图书的推荐评分。在本研究中，假设借阅时间越长意味着学生对该图书的满意度越高。因此，采用离散化方法将每位学生的借阅时间分割成等时间宽度的1至5的数值，数值越大，满意度越高。时间宽度的计算方法为式(6)，

(6)

在本研究的数据集中，最长的累计借阅时间为408天，而最短的累计借阅时间为1天。采用式(6)的方法计算不同借阅时间所对应的离散化时间宽度值，即偏好评分。计算结果如表1所示。

表1 转换后的偏好评分表

采用均方根误差(RMSE)作为评价评分准确度的离线指标[12]。对原始评分矩阵和转换后的评分矩阵进行RMSE计算，结果如表2所示。由表2可知，转换后的评分矩阵要优于原始评分矩阵。

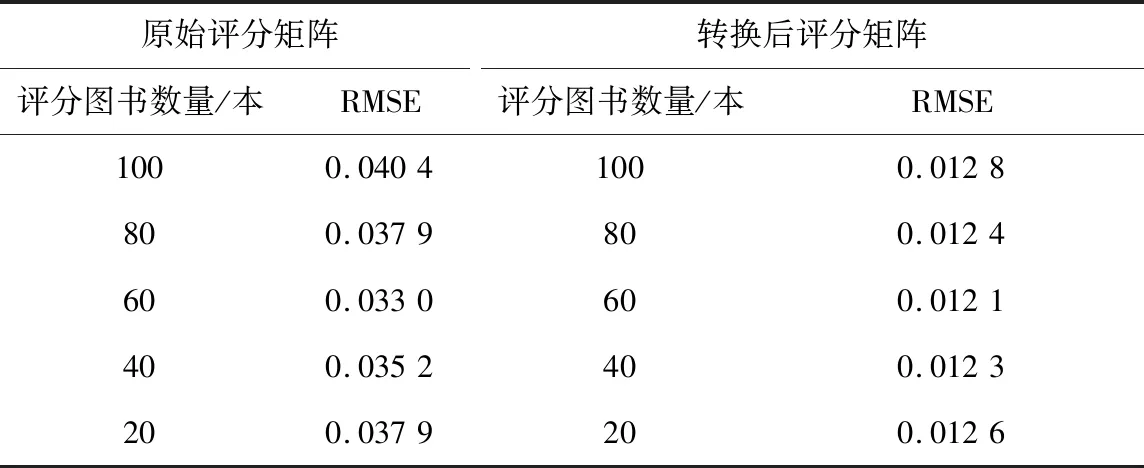
表2 不同数量图书的RMSE比较

步骤二：采用矩阵分解法来探讨影响每本图书与学生兴趣之间相关性的潜在因素。由于协同过滤数据会表现出较大的系统性倾向，即有些学生给出的评分整体比其他学生高，有些类型图书(例如小说)比其他类型图书更受学生欢迎，因而评分整体更高。直接使用评分数据进行预测会导致较大的偏差。因此本研究在评分计算式中引入的偏差值来解决这个问题。包含偏差的评分ru,i计算用式(7)[13]。

bu,i=μ+bi+bu

(7)

式中，μ表示整体平均评分，bu和bi分别表示学生u和图书i的评分偏差。然后，学生i对图书i的近似评分为式(8)。

(8)

式中,qi表示图书与其隐特征的关联程度，pu表示学生对图书隐特征的偏好程度。

步骤三：使用皮尔逊相关性系数、余弦相似度和欧式距离，计算每个待预测学生与每个其他学生之间的相似度。

步骤四：根据相似度得分，然后选择与待预测学生最相似的k名学生，并通过使用k位相似学生的图书偏好评分来预测指定学生对指定图书的评分。

步骤五：将3本具有最高偏好评分的图书推荐给待预测学生。

根据步骤一的图书偏好评分数据，可以计算每个学生的相似度评分。但是，由于评分矩阵非常稀疏，因此仅获得了很少的相似度评分，如表3所示。

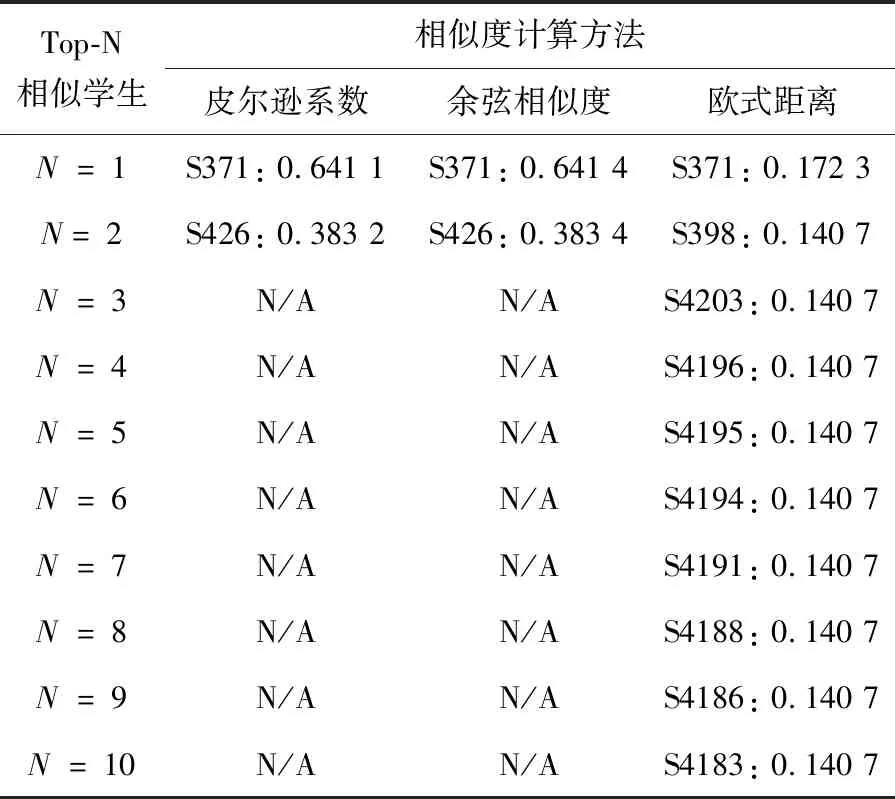
表3 没有经过矩阵分解的学生的相似度评分

为了处理表3所示的稀疏数据问题，本研究首先用零填充缺失的值，然后应用偏差矩阵分解法对评分矩阵分解，最后计算活跃学生与其他学生之间的相似度评分。计算结果如表4所示。

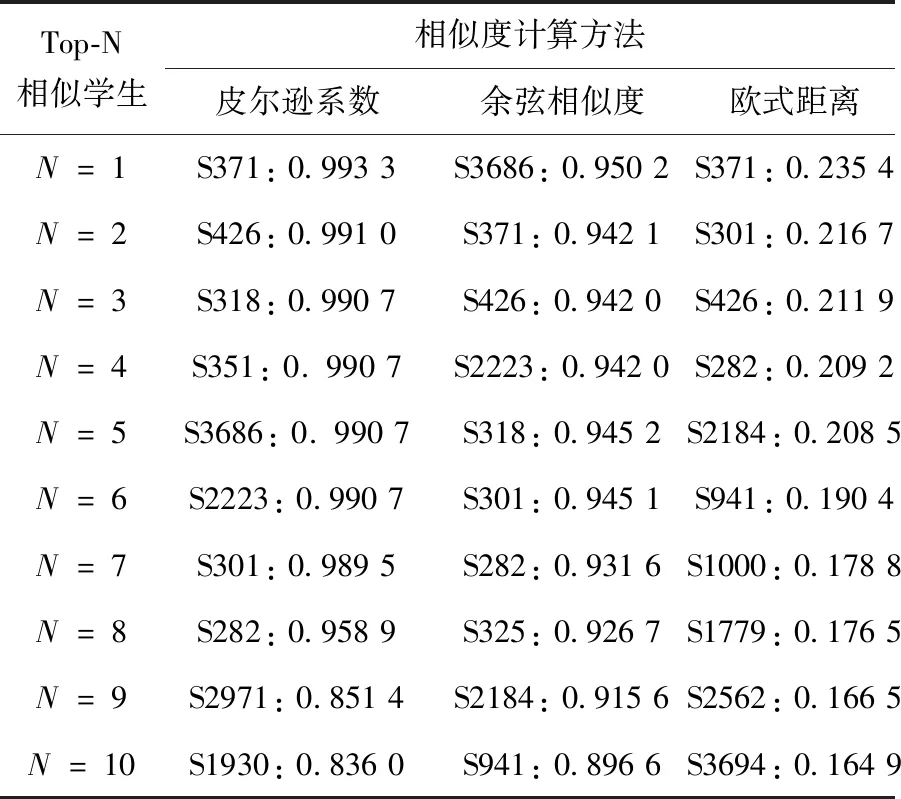
表4 经过矩阵分解的学生相似度评分

表4显示了通过各种相似度计算方法获得的学生的相似度评分的示例。对皮尔逊相关系数和余弦相似度两种计算方法所得出的结果略有不同。对于皮尔逊相关系数方法，前3名相似度得分的学生分别是S371、S426和S318，相似度分别为0.993 3、0.991 0和0.990 7。余弦相似度方法的结果表明，前3名相似度得分的学生分别是S3686、S371和S426，相似度分别为0.950 2、0.942 1和0.942 0。另一方面，基于欧式距离的前3名相似度评分学生分别是S371、S301和S426，相似度分别为0.235 4、0.216 7和0.211 9。

完成学生的相似度计算后，就可以依据偏好评分为学生推荐图书。评分如表5、表6所示。具有最高偏好评分的3本图书会被推荐给待预测学生。

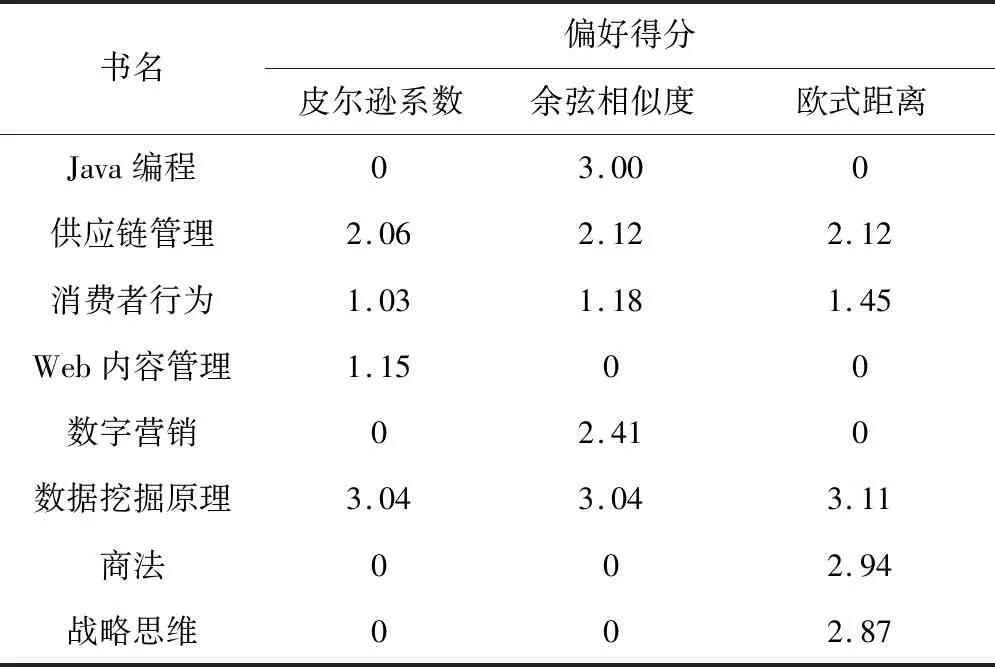
表5 使用N=35的领域的指定图书偏好评分

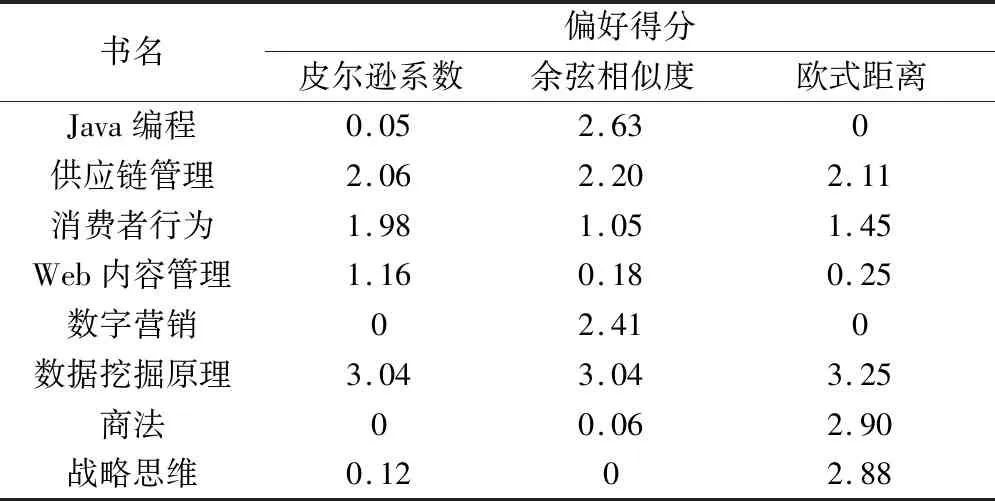
表6 使用N=40的领域的指定图书偏好评分

3 实验结果

使用式(9)的计算结果作为推荐系统准确度的离线评价指标，

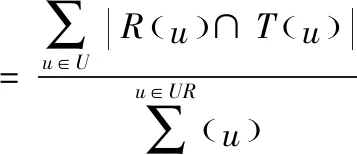
(9)

式中,U是学生集合，u是待预测学生，R(u)是根据训练数据集的偏好评分数据给学生u做出的图书推荐列表，T(u)是在测试集上的推荐列表。

实验将推荐图书的评分分数与学生实际借阅的书进行了比较,以验证每种方法的性能。比较结果如表7所示。实验结果表明，基于皮尔逊相关系数所得出推荐结果精确度最佳。余弦相似度方法稍逊于皮尔逊相关系数方法，欧式距离方法的精确度最低。

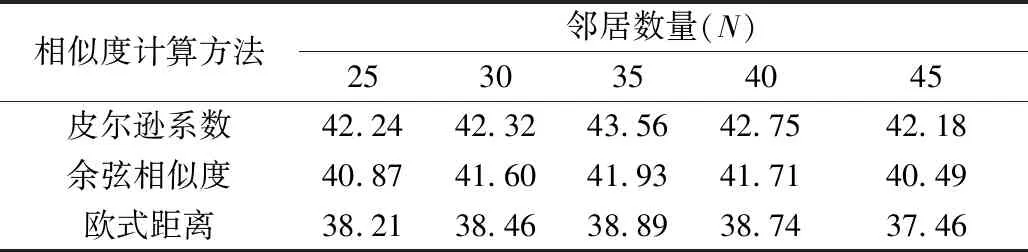
表7 3种相似度计算方法的准确性比较 (单位：%)

采用用户满意度作为评价图书推荐系统准确度的在线指标。因此，本实验统计了学生对所推荐图书的喜爱程度。从训练数据集的借书记录中随机抽取了20名来自不同年级和专业的学生。根据预测的偏好评分值，向这些学生推荐3个具有最高偏好得分的图书。然后要求学生从以下5个量化数值中选择一个数值来描述他们对推荐图书的喜爱程度：5.很感兴趣；4.有点兴趣；3.中立；2.不太感兴趣；1.完全不感兴趣。

在邻域大小(N)为35的情况下计算推荐图书，然后对20名学生的满意程度进行统计，结果如表8所示。使用皮尔森相关系数方法、余弦相似度方法和欧式距离方法所推荐图书的获得学生很感兴趣的人数(比例)分别为：9人(15.0%)、8人(13.3%)和7人(11.1%)。

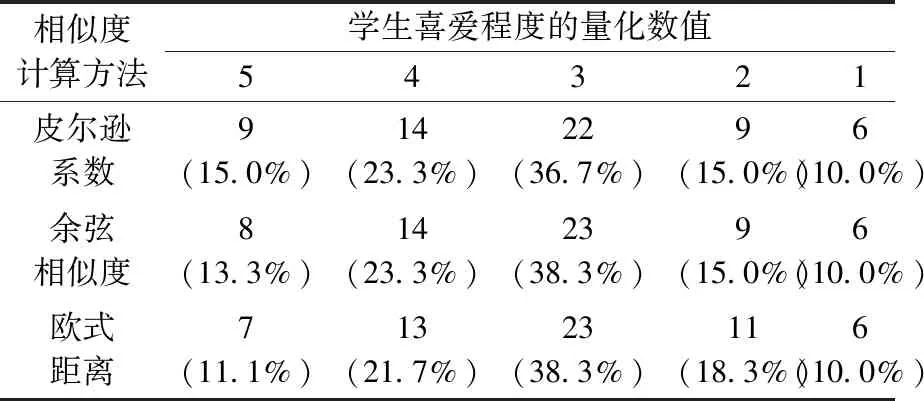
表8 3种相似度方法所推荐图书对学生吸引程度的对比

4 总结

本研究使用协同过滤技术构建了面向图书馆的图书推荐系统。读者偏好评分矩阵是根据带有时间戳的借阅记录和相应的归还记录构建的。此外，本研究还通过矩阵分解技术来解决数据稀疏性问题，通过引入偏差值来对评分的系统性误差进行纠正。实验结果表明，该图书推荐系统的准确度是可以接受的。未来，本研究计划通过利用图书属性(如类别、出版商、作者)和学生的个人资料(如学院、学年和专业)进一步提升图书推荐系统的准确度。