基于GP-DINA的教师继续教育的自适应学习系统设计
赵宇丹
(广州开放大学,网络与信息中心,广东,广州 510000)
0 引言
在现有的教育模式的研究中,文献[1]分析了成人本科学士学位英语的教育问题,根据自适应学习的工作原理,设计了成人本科学士学位的英语自适应学习系统。为了保证系统的稳定运行,从知识图谱、认知能力测评和推荐引擎3个方面进行了优化,最后在北京邮电大学网络教育学院对系统进行了应用,应用结果表明知识图谱技术的引入能够提高成人本科学士学位的英语教育效果。但是使用该系统学习之前需要对学生进行测评,只是通过测评的分数来对用户的掌握程度进行认知,这种对用户的认知并不准确,会导致个性化学习的目标不准确。文献[2]将自适应学习系统运用到不同风格学习者的眼动模型研究中,首先根据自适应学习原理提出了基于眼动模型的自适应学习框架,此框架能够分析不同认知风格学习者的眼动模型差异。考虑到眼动行为中注视总持续时间和注视点数量,构建了基于眼动追踪的在线学习者认知风格识别模型。这种方法虽然为自适应学习系统的应用和开发提供了新的思路,但是无法根据学习者实现多级评分。
基于以上内容,本研究根据教师继续教育现状,结合互联网技术和人工智能技术,设计了一个教师继续教育自适应学习系统。
1 教师继续教育自适应学习系统设计
教师的继续教育应该包括两个方面:知识学习和综合素质的培养[3]。因此,相比对学生的教学系统,教师的继续教育系统会更加复杂。自适应学习理念是人工智能与教育领域相互结合的产物,其目的在于根据学习者的实际情况,推荐适合学习者的学习任务或者课程[4],根据教师继续教育的内容,作者设计了一款自适应学习系统,其实现过程如图1所示。

图1 自适应学习系统的实现
自适应学习系统的实现一般分为3个部分:学习者认知、知识图谱构建和学习推荐。
学习者的认知阶段是根据学习者在系统的个性化搜索、学习数据以及登录系统所录入的学科信息通过GP-DINA模型实现对学习者的多级评分,最后通过计算综合得分来完成对学习者的认知,这关系着系统推荐的内容和知识图谱的构建,根据不同风格的教师,能够推荐针对性的学习内容和课程[5]。
知识图谱的构建主要是根据教师的学科分类将学科的重点知识构建成一个图谱网络,是根据教师继续教育目的的。本研究的知识图谱会增加一些教师的综合素质知识,比如英语水平、普通话水平、身体健康状况、应急事件的处理能力以及多种专业学科技能等。每个学习者的知识图谱会根据教师的专业能力和综合素养的不同,通过知识的关联性分析,构建个性化的知识图谱[6]。
学习内容和课程的推荐采用的是推荐算法,目前应用较为广泛的推荐算法有基于用户的推荐算法、基于内容的推荐算法和基于用户和内容的推荐算法。因为本研究中需要解决的问题是提高教师继续教育的质量,同时根据推荐的准确率,所以选择了基于用户行为的协同过滤推荐算法作为学习内容推荐手段[7-8]。
2 教师继续教育知识图谱的构建
知识图谱是一种结构化的关系网,它能够将实体知识与其之间的相互关系以网络图的形式表现。其网络结构如图2所示。
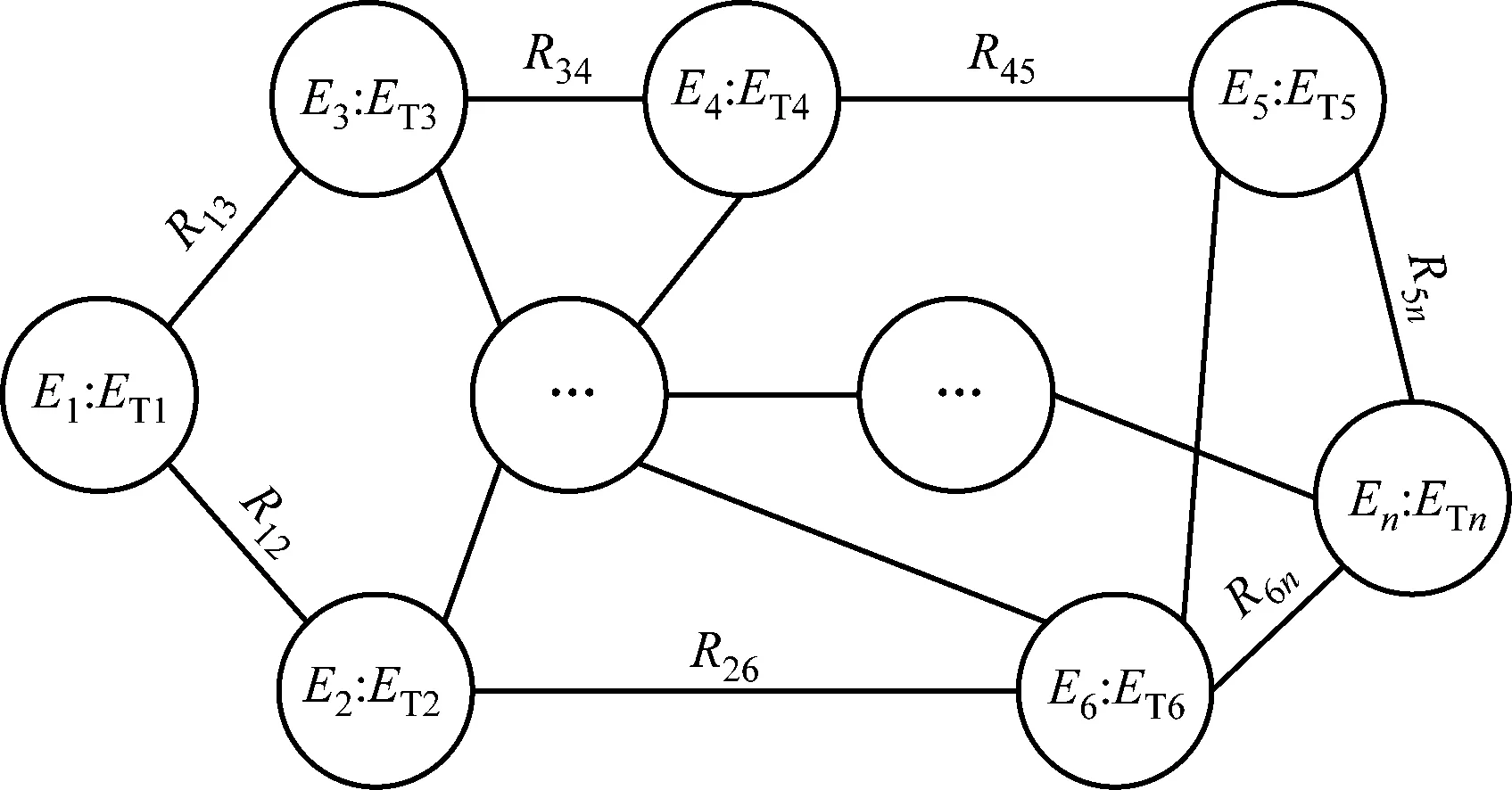
图2 知识图谱结构
为了更好地理解知识图谱,这里引入一个 “实体-关系-实体”或者“实体-属性-属性值”的三元组来表示知识与知识之间的相互关系,其中,所有的实体都会有一个独有的ID标识,属性和属性值是用来对某一个知识的深度解读,知识网络的形成是依靠不同知识实体之间的内在联系和关系。在教师的继续教育中,知识的最小单元的表现形式通常为课程,因此将课程实体作为本研究中知识图谱构建的基础。将本研究中的三元组表示为T,通过数据集合表示有T={E,R,ET},其中E表示不同课程实体的数据集合;R表示不同课程实体之间的关系集合;ET表示不同课程实体之间存在的知识内在属性。图2中,Ei为具体的实体课程,;Rij为课程Ei与课程Ej之间的内在联系;ETi为课程Ei的内在属性集合。知识模型的架构如图3所示。

图3 知识模型架构
图中虚线部分为教师继续教育自适应学习系统的知识图谱形成过程,其他部分负责知识图谱的更新或补充。
3 基于GP-DINA模型的多级评分认知诊断模型
假设一次测试中需要测量的属性有K个,J为项目的数量。用QJK=(qjk)来表示属性和项目之间的关联矩阵。其中,如果项目j已测试有属性k,则用qjk=1来表示,否则用qjk=0来表示。除此之外,用αi=(αi1,αi2,…,αiK}来表示参加测试教师i属性掌握情况,如果参加测试的教师对属性k已掌握,则用αik=1来表示。基于以上内容,潜变量的表达式为式(1),
(1)
式中,ηij为测试中的理想反应,其数值在参加测试老师i已掌握j项目中的各属性时为1,其他为0。
综上,DINA模型可以表示为式(2),
(2)
式中,sj表示的是滑动参数,即参加测试的老师失误答题的概率;gj表示的是参加测试的老师猜测答题的概率;Pj(αi)表示的是参加测试的老师答对项目的概率。

(3)
(4)
根据式(3)、式(4),可以得到潜变量的定义式(5),

(5)
式中,i表示一级分类,j表示二级分类,m表示j下的理想得分,则GP-DINA模型可以表示为式(6)。
(6)
需要注意的是,如果遇到特殊情况,每个属性具有相同的权重时,每个属性的价值都被取值为1。因此,潜变量进一步可以变化为式(7)。

(7)
模型相应变化为式(8),
(8)
4 试验仿真与分析
4.1 认知诊断模型的仿真与分析
在实验室内使用计算机对上述模型进行仿真,使用的计算机配置处理器型号为Inter Core i5-9700F,运行内存为16G,硬盘大小为1T,操作系统为Windows10。采用MATLAB对上述的算法进行仿真和测试。
假设参加测试的老师i的知识状态为α,则存在条件概率为式(9),
(9)
本研究中每个属性之间不存在任何的层级关系,边际似然函数可以表示为式(10),
(10)
式中,p(αl)为先验概率;αl为知识状态。根据极大和对数似然函数的相关概念,可以得到式(11)

(11)
式中,Ij(t|m)表示参加测试老师的平均人数。通过迭代计算,可以得到滑动概率的有效估计值。一共选取了35道题,其中,2道6分题,4道 5分题,5道4分题,6道3分题,8道2分题,10到1分题,设置参加测试的老师人数为3 000人,假设参加测试的老师都是采用理想反应模式(知识掌握情况)作为其观测反应模式,在35道题中随机抽取题目对老师进行考查,循环15次。选取滑动概率为0.36对无结构型的层级结构分析,循环15次,计算每种属性的均值和方差,计算边际判断准确率和模式判断准确率,将数据整理可以得到如表1所示的数据。

表1 滑动概率为0.36的诊断结果
表1中A1-A6为属性,根据表中的数据可知,A1属性的属性判断准确率相比其他属性较高,因为A1处于较高的层次,其他的属性层次相同,所有其他属性的属性判断准确率的水平基本相同。
由于篇幅的原因,只对属性的边际判断准确率和模式判断准确率进行整理,整理得到如表2所示的属性边际判断准确率数据,不同滑动概率下的属性边际判断准确率如表2所示。
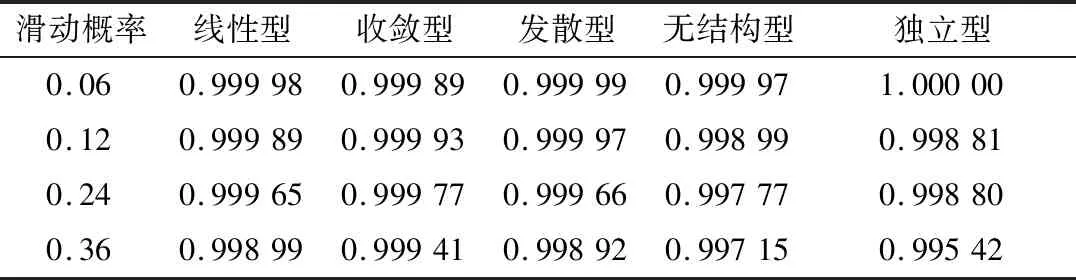
表2 不同滑动概率下的属性边际判断准确率
从表中的数据可以知道,在滑动概率为0.06时,不同层级结构的属性边际判断准确率基本相同,随着滑动概率的增大,所有层次的边际判断准确率都有所下降,但总体效果依然较好。
不同层次下的不同滑动概率模式判断准确率如表3所示。
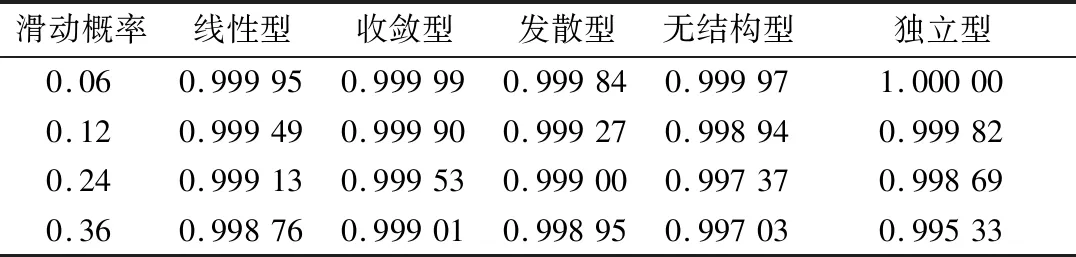
表3 不同滑动概率下的模式判断准确率
从表中的数据可以看出,在滑动概率为0.06时,5种不同层次的模式判断准确率基本相同,随着滑动概率的增加,模式判断准确率有所下降,但是没有低于0.998,说明总体的判断效果较为准确。
4.2 自适应学习系统的应用效果分析
将本研究中的教师继续教育自适应学习系统在某市教育系统中进行试运行,试运行时间为6个月。调取其中一次的培训数据,此次培训科目为英语,参加培训的老师一共有10人。以培训开始前进行的认知测试作为对比因素,在培训完成后对所有的老师再进行一次测试,测试题目与之前的摸底考试难度一致,可以得到表4所示的成绩对比数据。

表4 参加培训教师的前后成绩对比
从表4中的数据可以看出,10名教师的成绩都有所上涨,其中8号教师的成绩上浮最大,增加了14.5,10号教师的成绩上浮最小,为2.6,可能是因为8号教师的原本成绩并不理想,所以上升的成绩较多。根据学生们对老师参加培训的综合素质进行打分,满分为5分,通过长时间的统计,可以得到表5所示的数据。

表5 学生评价数据
从表5中的数据可以得到,10名参加培训的教师的学生评价都有所提高,为了提高数据的说服力,将6个月内所有教师的学生评价进行统计,可以得到图4所示的学生评价对比图。
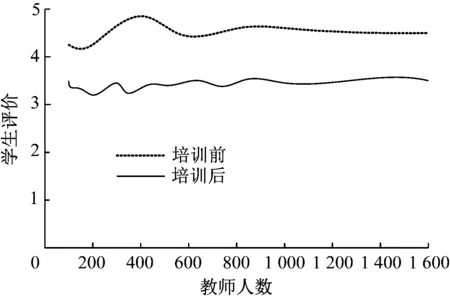
图4 学生评价对比
从图中可以看出,培训前的平均值为3.5,培训后的平均值为4.5,平均提高了1。
5 总结
本研究根据现有的教师继续教育现状,从教育模式出发,结合DINA模型,设计了一个教师继续教育自适应学习系统,通过试验与仿真,证明了DINA模型改进部分的可行性,也证明了自适应学习系统的性能,在教师继续教育领域值得大面积推广使用。但是由于试验时间较短,可能依然会存在一些不足,在后续的使用过程中需要进行不断的改进和完善。

