新建盾构隧道近距离侧穿既有隧道相互影响分析

胡 静 何志坚 王一洋 罗学东

（1.武汉地铁集团有限公司，湖北武汉 430000；2.中国地质大学(武汉)工程学院，湖北武汉 430074）

0 引言

近年来，城市地下交通在我国各大城市迅猛发展，众多的地下隧道不可避免地会出现两隧道相交或并行等情况。新建隧道的施工会对周围土体产生扰动，使既有隧道的结构发生变形，若既有隧道变形过大，则会出现较大的安全隐患。

国内外学者针对两隧道近接开挖过程中可能出现的安全隐患开展了大量的研究。卢岱岳等[1]将理论计算与实际工程数据相结合，揭示了新建隧道近距离上穿施工时既有隧道的纵向变形规律。刘树佳等[2]研究了新建盾构隧道施工在三种不同的条件下对既有隧道管片变形的影响。梁荣柱等[3]通过建立隧道纵向变形平衡微分方程，同时基于有限差分原理，得到了隧道的变形数值，并结合工程实际情况，验证了该计算方法的可靠性。张海彦等[4]使用有限元分析软件分析了在不同间距下新建隧道对既有隧道的变形影响。武永珍等[5]先通过数值模拟软件计算出不加固工况下新建隧道对既有隧道变形影响的规律，而后对交叉结点洞内进行加固处理后，发现其变形明显降低。高利宏[6]利用软件模拟并结合工程实例确定了新建地铁施工过程中对既有隧道的变形控制标准。许有俊等[7]对新建地铁隧道上穿既有隧道建立数学模型分析，推导出地铁隧道变形计算公式，并使用此公式对实际工程进行预测。刘庆丰等[8]结合数值模拟以及现场监测等方法，研究双线并行下穿临近既有隧道周围地层的影响规律，提出盾构近接相关施工控制技术。Avgerinos 等[9]利用三维有限元软件研究了新建隧道下穿既有隧道时既有隧道内环向力、弯矩以及衬砌结构的变化。Han 等[10]利用ANSYS 有限元分析软件，对新建隧道在施工过程中相邻既有隧道的位移和应力进行分析计算，同时分析了隧道内衬砌对计算结果的影响。Wang 等[11]主要研究浅埋流变性地层中新老隧道的相互作用。Xue[12]分析了开挖面与既有隧道水平距离不同时，开挖面极限支护力的变化以及开挖面支护力对既有隧道和地表沉降的影响。Lin 等[13]采用数值模拟的方法研究了既有隧道斜交施工的变形行为，还进行了参数研究，分析了新旧隧道交叉角对既有隧道变形行为的影响。

本文以武汉市轨道交通5 号线近距离平行侧穿2 号线工程为例，建立三维有限元模型，分析既有隧道在盾构隧道开挖前后的变形量，同时在既有隧道内施加列车动荷载，与实际监测数据对比，研究新建盾构隧道施工与临近既有隧道之间的相互影响。研究结果可为今后类似工程提供参考依据。

1 工程背景

武汉市轨道交通5 号线一期工程积玉桥站-新生路站区间位于武昌区和平大道，该区间起点为新生路站，线路沿和平大道铺设，沿线跨前进路、健康路及新生路，向南延升至积玉桥站。拟建区间与2 号线积玉桥站-江汉路站区间在起点里程右DK13+666.846-右DK14+255.610 段属于并行关系，结构间距最小值为5.0 m，属于近距离并行施工，且此区间内两隧道拱顶埋深为12 m，盾构施工时对临近既有隧道以及周边建筑物都将造成不可忽视的影响，盾构施工难度较大，安全风险较高。两隧道平行段示意图见图1。

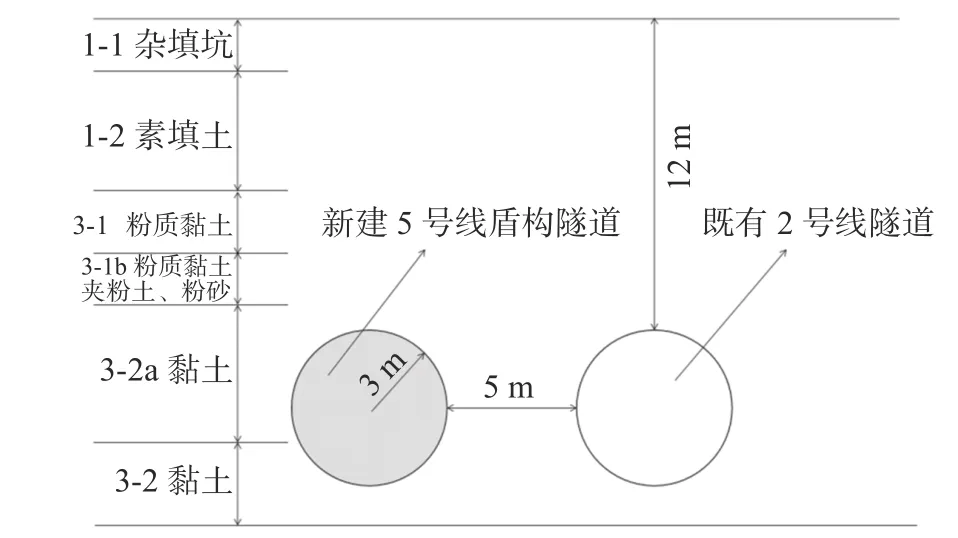
图1 两隧道平行段示意图

2 新建隧道近距离侧穿既有隧道数值模拟分析

2.1 模型建立

采用FLAC3D 软件建立两隧道并行段数值模型。模型选取积玉桥站-新生路站区间DK13+936-DK13+996 段（共计60 m）为研究对象。两隧道并行段数值模型与两隧道正视图见图2、图3。

图2 新建隧道与既有隧道并行段数值模型

图3 新建隧道与既有隧道并行段模型正视图

该模型的模拟步骤如下：

（1）建立模型，计算初始应力；（2）将初始位移清零；（3）开挖既有隧道，计算既有隧道应力情况，位移清零；（4）进行新建隧道盾构开挖，每次开挖3 m 边开挖边施作管片和注浆；（5）重复（4）步骤，直到隧道开挖到60 m，结束计算；（6）在既有隧道中施加列车动荷载之后，重复以上工况。

2.2 参数选取

本模型对隧道实际情况进行简化，使用摩尔-库伦模型，选取尺寸为100 m×60 m×84 m 的地层模型；隧道管片使用弹性本构模型，密度为2500 kg/m3，弹性模量34.5 GPa，泊松比为0.17，由于管片连接处刚度会有部分损失，因此管片刚性折减系数取0.85。模型计算中初始应力仅考虑重力，地下水折算入土层重度中。其中隧道管片外径6.20 m，内径5.50 m，厚度0.35 m，隧道管片宽度为1.5 m，新生路站至积玉桥站区间隧道拱顶埋深为12 m。由于既有隧道建成时间较长，因此将既有隧道初始位移设置为零。本文模拟盾构施工长度为60 m，管片宽度以1.5 m 考虑，盾构开挖模拟共20 步，模拟过程中盾构机每一步推进3 m，盾构机每次推进完成后即刻加装管片，随后进行注浆加固处理，其中注浆压力为0.22 MPa，注浆厚度为0.2 m。

根据钻孔资料、原位测试、室内试验、物探分析结果，结合区域地质资料，本区自上而下分布依次有杂填土、素填土、粉质黏土、粉质黏土夹粉土、粉细砂、粉土、粉质黏土互层、强风化粉砂质泥岩。本模型中隧道所穿越的地层主要为3-2a 和3-2 黏土层。穿越土层物理力学参数见表1。

表1 土层物理力学参数表

2.3 计算结果分析

2.3.1 新建盾构隧道施工对既有隧道竖向变形影响分析

由于新建隧道与既有隧道临近平行且最小距离仅为5 m，新建隧道施工所造成的土体扰动必然对既有隧道的结构产生影响，因此监测既有隧道的拱顶变形极为重要。根据数值模拟的结果，在盾构隧道开挖20 步结束后，可以得到既有隧道的竖向变形云图，如图4所示，其最大沉降量为5.33 mm，未达到预警值。

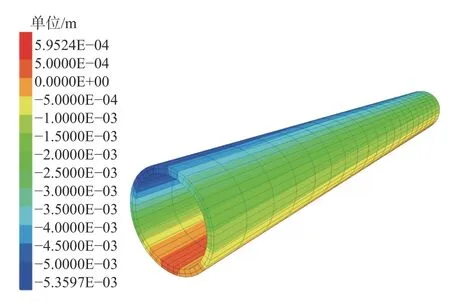
图4 既有隧道竖向位移云图

为进一步探究新建盾构隧道施工对既有隧道顶部变形的影响，令新建隧道初始开挖位置为0 m，选取既有隧道顶部7 m、19 m、31 m、43 m 和55 m 处在盾构施工过程中的位移情况，得出既有隧道拱顶变形随时间变化的曲线图（见图5）。

图5 盾构施工对既有隧道不同位置处拱顶竖向变形影响曲线图

由图5 可知，盾构隧道开挖时，既有隧道顶部沉降的变化速率是随盾构隧道开挖进度变化而变化的，即盾构隧道刚开挖时，既有隧道顶部靠近盾构区域处开始出现沉降，并且离盾构施工区域越近处，顶部沉降变化速率越快，并且在盾构区域远离之后，此部分顶部沉降速率开始变缓，最终趋于平稳。

盾构隧道施工时会对既有隧道产生影响，越靠近盾构隧道，既有隧道受其影响越大，因此既有隧道中沉降量最大处并非位于隧道顶部，而在左拱腰处，最大值为5.33 mm，而隧道顶部沉降量最大值为4.70 mm。同时由图4 可以看出既有隧道底部隆起量最大值为0.60 mm，此变形量在工程中相对可控，对既有隧道地铁轨道和线路运营的影响不大。

2.3.2 新建盾构隧道施工对既有隧道水平变形影响分析

盾构隧道施工对既有隧道水平变形的影响如图6所示，可以看出最大水平位移为2.51 mm，远离盾构隧道方向，且未超过预警值。

图6 既有隧道水平位移云图

为进一步了解新建盾构隧道施工对既有隧道水平变形的影响，令新建隧道初始开挖位置为0 m，选取既有隧道距新建隧道最近侧和最远侧7 m、19 m、31 m、43 m 和55 m 处的水平位移情况，分析盾构施工对既有隧道水平位移的影响（见图7、图8）。

由图7 可以看出，各曲线的峰值点均为新建盾构隧道掌子面所在区域，而后在盾构管片后注浆减小了土体的扰动，因此既有隧道水平变形量略微减小，最终维持稳定状态。从图8 可以看出，远侧点位最大水平变形量为-0.13 mm，远小于近侧点位变形量，因此相较于既有隧道左侧，右侧变形可以忽略不计。

图7 盾构隧道对既有隧道近侧水平变形影响曲线图

图8 盾构隧道对既有隧道远侧水平变形影响曲线图

盾构隧道对既有隧道的变形影响是一个累积的过程，随着盾构开挖的进行，既有隧道的水平变形量也越大，如图7所示，既有隧道在7 m、19 m、31 m、43 m、55 m 处的水平变形最大值分别为1.74 mm、1.84 mm、1.74 mm、1.77 mm、2.19 mm，均未超过工程预警值，同时相对拱顶沉降量要小，因此在既有隧道中所造成的影响极小，对地铁运营影响相对可控。

2.3.3 既有隧道列车动荷载对新建隧道拱顶变形影响分析

考虑到既有地铁隧道在运营过程中列车行驶产生的震动可能会影响盾构隧道的施工，因此本文在原有的模型基础上施加列车动荷载，以便于探究列车动荷载对新建盾构隧道拱顶变形的影响。

本文对列车动荷载采用能够反映其周期性的激振力函数进行模拟。梁 波等[14-15]考虑到列车的各项数据、车速以及轨道状况等情况，利用静荷载与动荷载相结合的方式，用激振力函数表达出了列车动荷载周期性的特点：

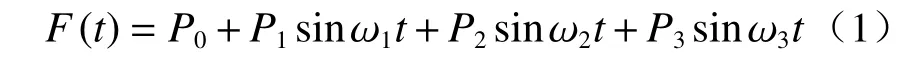
式中：P0为车轮静载；P1、P2、P3分别对应几何不平顺控制条件下某种典型值的震动荷载；ω1、ω2、ω3分别为对应车速下各自不平顺振动波长的圆频率。

其中振动幅值及圆频率的计算公式为

式中：M0为簧下质量；ai为对应条件下几何不平顺矢高；ωi为对应条件下振动圆频率；v为列车运行速度；Li为对应条件下的几何不平顺波长。

参考武汉地铁2 号线列车数据，本次数值试验中选用的几何不平顺取值与列车相关参数见表2、表3。

表2 几何不平顺取值表

表3 列车相关参数表

武汉地铁2 号线列车动荷载激振力函数：

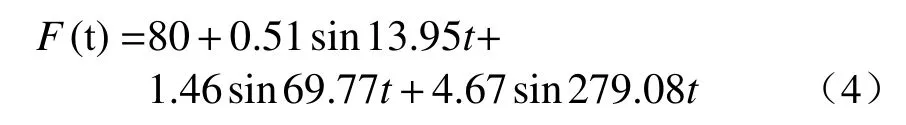
在前文模型的基础上，在既有隧道内施加列车动荷载函数，并切换模型边界条件，在模型边界处施加静态边界，用于吸收动荷载传播到边界所产生的反射波，以免反射波干扰计算结果，并设置局部阻尼用于模拟在实际情况下波的传播方式。

本文在每次开挖步后施加动荷载计算，计算时令新建隧道初始开挖位置为0 m，取盾构隧道内19 m和43 m 处的拱顶变形值，并设置一组未施加动荷载的模型作为对照，最后得出的对比图见图9。

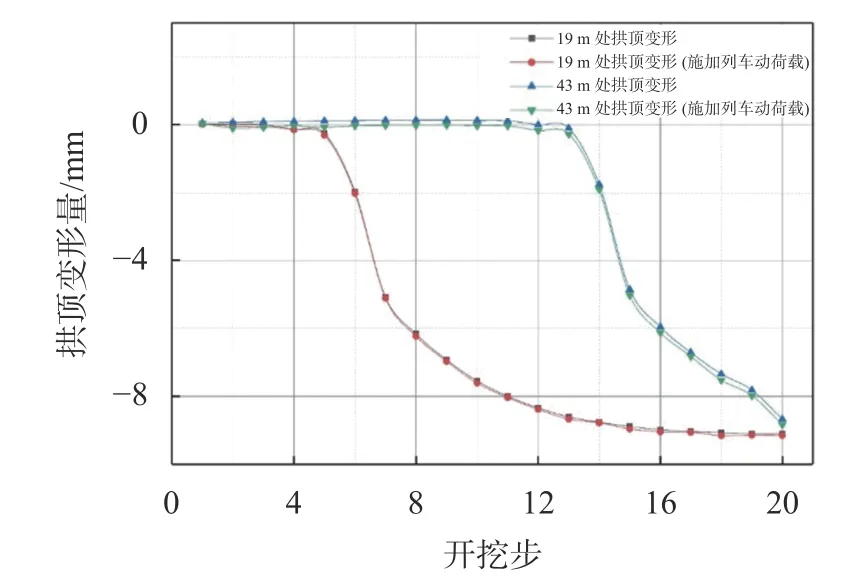
图9 盾构隧道拱顶变形在施加动荷载前后对比图

从图9 的对比中可以看出，在施加列车动荷载之后，盾构隧道的拱顶变形曲线与未施加动荷载时极其相似，且拱顶变形量变化极小，变化量的平均值在0.1 mm 左右，此变形相较于盾构开挖时隧道拱顶的变形可忽略不计，因此既有隧道的列车动荷载对盾构隧道的影响极小。

3 现场监测对比分析

3.1 监测点位布置

新建盾构隧道部分路段与既有2 号线存在近距离并行关系，可能对2 号线运营产生影响。因此将使用精密水准仪对已运营2 号线拱顶竖向位移进行监控量测。现场沿隧道方向使用精密水准仪在隧道顶部进行拱顶竖向位移的监测，每20 m 设一个断面，共156 个测点。已运营2 号线隧道断面监测点布置见图10。

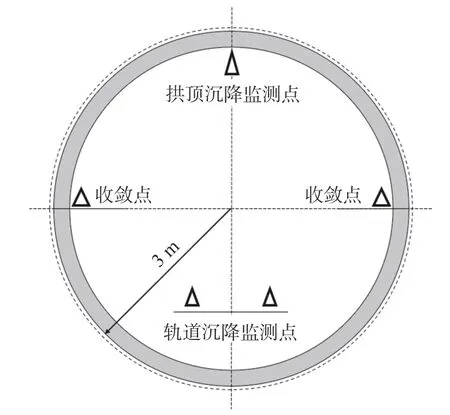
图10 已运营2 号线区间左隧道断面监测点布置图

3.2 监测结果分析

由于本工程实例中盾构隧道的左右两线路平行近接2 号线既有隧道的左线，忽略新建隧道对既有隧道右线的影响，因此本次研究仅考虑右线贯通后对既有隧道的结构变形影响。

依据之前的数值模拟模型，选择里程为左DK13823.346-左DK13863.346 的监测数据进行分析，此时选择的监测数据位于455 环、468 环、481 环上，对从2020年1月1日到1月10日连续10 天的既有隧道拱顶监测数据进行分析，现场监测拱顶变形见图11。根据现场盾构机的掘进速度，将数值模拟数据与现场监测数据在掘进环数条件下进行整合，见图12。由两图可以得出以下规律：

（1）离掌子面越近，盾构开挖所带来土体的扰动就越大，既有隧道拱顶变形速率也越大。从图11 中可看出，在监测时间内第455 环处离盾构隧道开挖掌子面最近，因此其在第5-7日拱顶变形速率最大；从图12 中可看出，在相同掘进环数内，数值模拟得出的变化曲线与现场监测数据曲线相似。

图11 既有隧道拱顶监测点连续10 天监测数据图

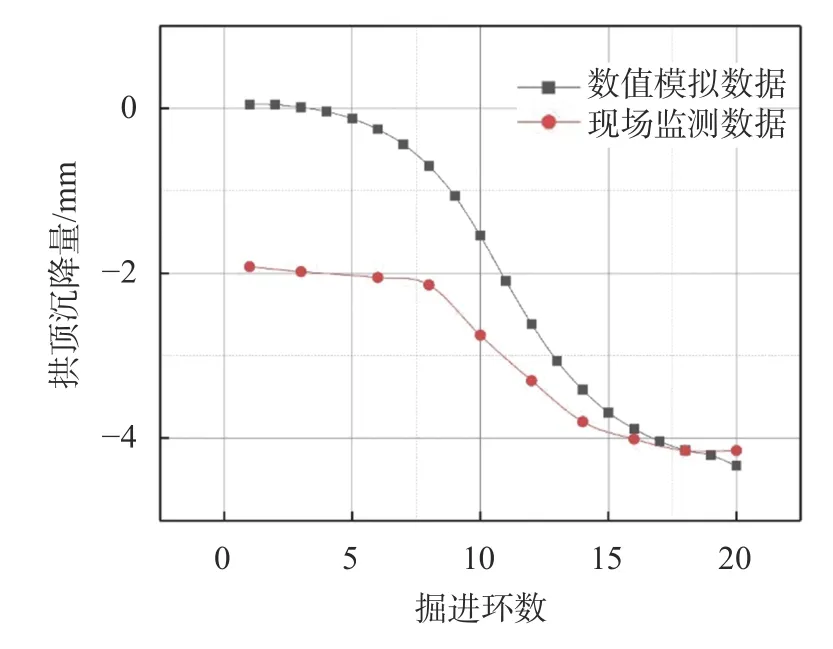
图12 数值模拟数据与监测数据对比图

（2）新建盾构隧道施工时，既有隧道拱顶沉降值曲线基本表现为前期和后期沉降值缓慢增加、中期沉降值相对增加较大的情况。

（3）现场监测数据中拱顶沉降量最大值为-4.15 mm，数值模拟中拱顶沉降量最大值为-4.70 mm，由于现场监测数据具有偶然性和误差性，并有离散状况，且在做数值模拟过程中对模型进行了简化处理，因此数值模拟与现场监测数据存在一定误差。但两者相差值在可接受范围内，且均未达到工程施工预警值，并未对2 号线既有隧道结构安全以及地铁运营造成影响，数值模拟能有效反映施工现场的实际情况。

4 结论

（1）既有隧道部分离盾构隧道掌子面越近，其拱顶沉降变化速率越大。既有隧道拱顶沉降量呈现出前期、后期沉降量变化速率较为平缓，中期变化速率较大的规律。

（2）新建隧道施工时既有隧道的水平变形为由两侧向隧道内凸，其中靠近盾构隧道部分的变形量远大于远离盾构隧道的部分，但两者变形量均在预警值之内。此外，根据现场监测数据的反馈结果判断，盾构施工对既有隧道水平位移影响在安全可控范围之内，盾构隧道施工期间2 号线地铁能维持安全运营。

（3）既有隧道中施加列车动荷载后，新建盾构隧道的拱顶沉降变化量约为0.1 mm，此变化量对实际盾构施工造成的影响极小，基本可忽略不计。