生化黄腐酸对盐碱土水盐运移特征的影响

孙 燕 王 建 王全九 曲 植 王春宏 张曦元

(西安理工大学省部共建西北旱区生态水利工程国家重点实验室， 西安 710048)

0 引言

土地盐碱化使得土壤通气性和透水性变差，延缓地表土壤温度的回升、降低土壤酶活性，对农作物生长及其产量产生一定的负面作用，威胁着农业可持续发展[1]。新疆是我国最大的盐碱土区，其盐碱化面积占全国盐碱土地总面积的1/3和新疆耕地面积的32.07%[2]。合理改善土壤盐碱化、提高盐碱化耕地的粮食生产水平对实现旱区农业可持续发展具有非常重要的现实意义[3]。目前，向土壤中添加化学改良剂(如脱硫石膏、硫酸亚铁等)是盐碱土改良常用的化学方法，主要通过改变盐碱土胶体吸附性阳离子的组成，调节土壤pH值，改善土壤结构和营养状况，进而达到改良盐碱土的目的[4]。然而添加上述化学改良剂可能会造成土壤的二次污染，如大量施用脱硫石膏会造成土壤重金属污染[5]，长期施用硫酸亚铁会造成土壤板结[6]等现象。

研究表明，施用黄腐酸(Fulvic acid，FA)能够改善土壤结构、降低土壤盐分、提高土壤养分有效性、增强作物抗逆性，进而促进作物生长，是一种绿色高效的盐碱土改良措施[7-14]。目前黄腐酸的制备主要是从褐煤、风化煤等矿物源中提取[15]，提取过程中需消耗大量的酸、碱等化学物质，甚至需要高压、高温等剧烈反应条件及严格的工艺技术，生产过程中会产生大量的废水和废气，不利于农业绿色发展[16]。同时，褐煤、风化煤等均属于不可再生资源，过度开采会破坏生态环境[17]。利用微生物技术对农业废弃物进行发酵、固液分离、提取、浓缩后生产生化黄腐酸(Biochemical fulvic acid，BFA)，具有使用原材料易于获取、价格低廉、制备周期短、无污染等优点，同时可以为农业废弃物再利用提供有效途径[18]。杨晓玲[19]研究表明，生化黄腐酸能够促进小麦幼苗根系生长，提高小麦幼苗叶片中的可溶性糖和可溶性蛋白含量。贾爱萍等[20]研究认为，生化黄腐酸能明显提高番茄的株高和生物量，并降低青枯病的发生率。杨宇等[21]研究发现，生化黄腐酸能够增加土壤团粒结构含量，提高小白菜干物质量。目前，生化黄腐酸相关研究主要集中在促进作物生长发育和增产等方面，而施加生化黄腐酸后的盐碱土水盐分布影响作物根系生长和分布，研究施加生化黄腐酸后的土壤水盐运移特征以及定量分析其入渗过程能够为揭示生化黄腐酸促进作物生长机理提供理论支撑。

因此，本文将不同施加量的生化黄腐酸与盐碱土混合均匀，采用一维垂直土柱入渗试验，研究不同生化黄腐酸施加量条件下盐碱土的入渗特征及水盐分布特征，分析生化黄腐酸对土壤入渗模型参数的影响，以期为改善农田水盐状况、筛选改良中度盐碱土的生化黄腐酸合理施加量提供理论依据。

1 材料与方法

1.1 试验材料

供试土样取自新疆维吾尔自治区库尔勒灌溉试验站0～20 cm表层土壤，将取回土样置于阴凉处风干，去除土样中的枯枝、残留物，过2 mm筛备用。土壤机械组成采用Mastersizer 2000型激光粒度分析仪(英国马尔文仪器有限公司)进行测定，土壤物理性砂粒、粉粒体积分数分别为85.37%、12.48%，依据国际制土壤质地分类标准，判定该土壤质地为壤质砂土。供试土壤初始体积含水率为0.007 8 cm3/cm3，饱和体积含水率为0.375 cm3/cm3，初始含盐量为9.49 g/kg，土壤pH值为9.18，属于中度盐碱土[22]。试验所用的生化黄腐酸为山东廊坊松本科技有限公司生产，棕色粉末状，BFA质量分数大于等于90%。

1.2 试验设计与方法

试验于2021年5月在西安理工大学省部共建西北旱区生态水利国家重点实验室进行，采用一维垂直入渗系统开展不同生化黄腐酸施加量的入渗试验。土壤入渗试验装置由马氏瓶、试验土柱、支架等组成，其中马氏瓶高度为50 cm、内径为8 cm；试验土柱高50 cm、内径为8 cm，底部设有排水孔。生化黄腐酸施加量分别为0、1、2、4、8 g/kg(以干土质量计)，每个处理设置3次重复。土柱装土高度为45 cm，以土壤容重(1.65 g/cm3)分9层(每层5 cm)装填，保证层与层之间充分接触，不出现分层。入渗开始前，向土柱顶部倒入定量的试验用水(淡水)，以减小累积入渗量的初始误差。试验开始时利用秒表计时，并定时记录马氏瓶水位和土柱湿润锋深度。由于试验初期湿润锋移动较快，试验数据记录按照先密后疏的原则。当土柱湿润锋深度达到30 cm(入渗深度为整个土柱长度的2/3)时，停止供水同时用吸管吸出土柱顶部积水。质量含水率采用干燥法((105±2)℃)测定，质量含水率乘以容重得到体积含水率。将干燥后的土样进行研磨并按照1∶5土水质量比进行浸提，将浸提液静置8 h后利用电导率仪(DDS-307型)测定其电导率，通过计算转换即可得到土壤含盐量。使用恒水头饱和导水率测定仪测定土壤饱和导水率。

1.3 入渗模型

为了分析生化黄腐酸不同施加量对入渗模型相关参数的影响，分别采用Philip入渗模型[23]、Green-Ampt入渗模型[24]和代数模型[25]分析添加生化黄腐酸后的土壤入渗特性。

均质土一维垂直入渗条件下，Philip入渗模型的累积入渗量表达式为

I=St0.5+At

(1)

在短历时情况下，式(1)可简化为

I=St0.5

(2)

式中I——土壤累积入渗量，cm

t——入渗时间，min

S——吸渗率，cm/min0.5

A——稳定入渗率，cm/min

Green-Ampt入渗模型研究的是初始干燥的土壤在薄层积水时的入渗问题，当入渗时间较短、积水深度较小时其表达式为

(3)

式中i——土壤水分入渗速率，cm/min

Ks——土壤饱和导水率，cm/min

Sf——概化湿润锋处吸力，cm

Zf——概化湿润锋深度，cm

对于短历时入渗，Philip入渗模型中的吸渗率可以根据Green-Ampt入渗模型中的饱和导水率Ks和概化湿润锋处吸力Sf表示[26]，即

S=2KsSf(θs-θi)

(4)

式中θs——土壤饱和含水率，cm3/cm3

θi——土壤初始含水率，cm3/cm3

一维垂直积水入渗的代数模型可以较好地描述累积入渗量和积水入渗后不同土层深度的含水率分布, 且模型中的参数容易确定, 具体表达式为

(5)

(6)

式中θr——滞留体积含水率，cm3/cm3

α——土壤水分特征曲线和非饱和导水率综合形状系数

Z——任意土壤深度，cm

θ——土壤体积含水率，cm3/cm3

1.4 土壤水分特征曲线模型

本试验根据饱和导水率、饱和含水率、累积入渗量与时间的关系数据，通过Hydrus-1D软件反推出Van Genuchten模型中的滞留含水率θr和形状系数n。Van Genuchten模型具体形式为

(7)

式中h——土壤水吸力，cm

1.5 数据处理与统计

试验数据均取3次重复的平均值，采用Office 2016进行数据处理及制图；Origin和SPSS 25进行模型参数拟合和统计分析，LSD法进行显著性检验(P<0.05)。

2 结果与讨论

2.1 生化黄腐酸对土壤水分入渗特征的影响

图1为不同生化黄腐酸施加量(0、1、2、4、8 g/kg)下湿润锋深度随时间的变化曲线。由图1可知，入渗初期，各处理湿润锋深度的差异并不显著(P>0.05)，随时间的增加生化黄腐酸逐渐发挥作用。在相同入渗时间下，湿润锋深度随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，当施加量为4 g/kg时，湿润锋深度最小。在180 min时，施加1、2、4、8 g/kg生化黄腐酸后的湿润峰深度相比于不施加处理分别降低10.01%、27.00%、33.67%、19.33%，各处理差异显著(P<0.05)。

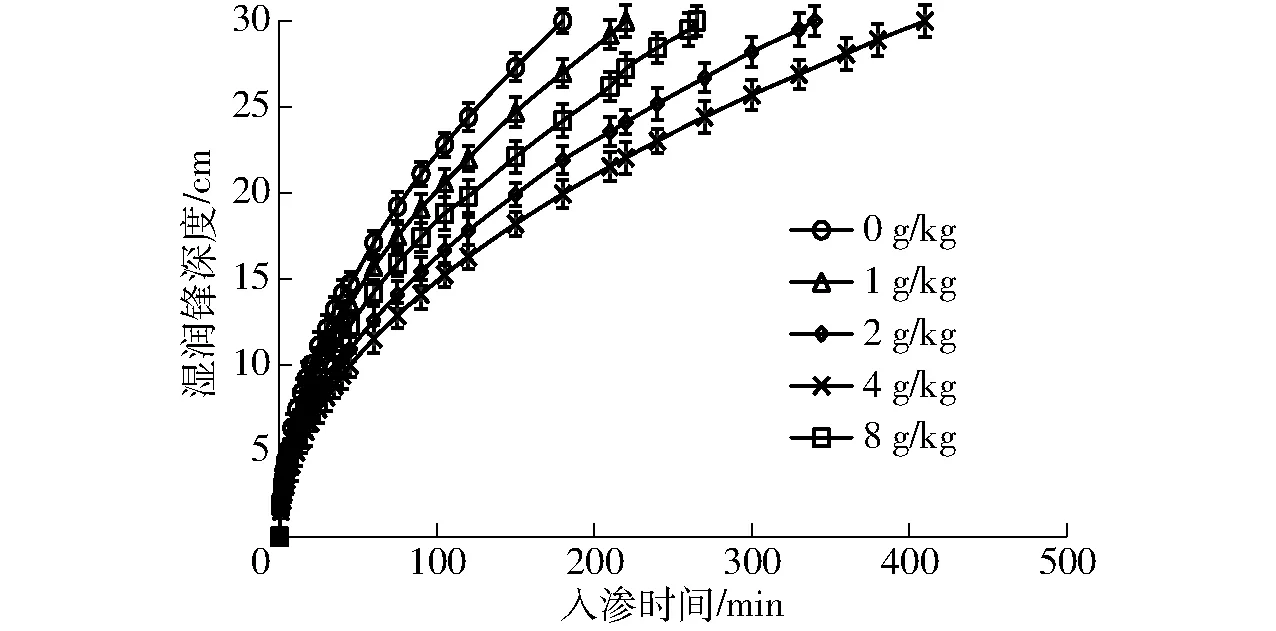
图1 不同生化黄腐酸施加量下土壤湿润锋深度变化曲线Fig.1 Variation curves of soil wetting front depth under different application amounts of BFA

图2为各处理下土壤累积入渗量和入渗速率随时间的变化曲线。由图2可知，入渗结束(湿润锋深度均为30 cm)后，土壤累积入渗量均随着生化黄腐酸施加量的增加呈现先增大后减小的变化趋势，生化黄腐酸施加量为1、2、4、8 g/kg后的土壤累积入渗量与未施加相比分别增加1.00%、4.67%、7.14%、3.44%，土壤水分入渗速率随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，各处理差异显著(P<0.05)。

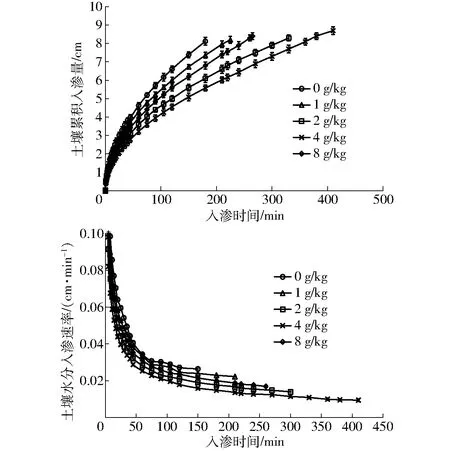
图2 不同生化黄腐酸施加量下土壤累积入渗量和水分入渗速率变化曲线Fig.2 Variation curves of soil cumulative infiltration and water infiltration rate under different application amounts of BFA

通过分析土壤累积入渗量和水分入渗速率发现，生化黄腐酸施入土壤后能够有效减慢土壤水分入渗速度和提高相同湿润锋深度下的土壤累积入渗量。产生的主要原因是由于生化黄腐酸可作为腐殖质中有机胶体施入土壤中[27]，在胶结作用下使土粒、微团粒相互团聚，促进了土壤团粒结构的形成[28]，改善了土壤结构和孔隙状况，从而改良了壤质砂土保水性差的特点；同时，生化黄腐酸本身含有大量羧基和羟基，能够溶于水后与水分子通过氢键结合形成网状结构，增加水的铺展面积[29]和粘滞性[30]，降低了水分入渗速率，使更多的水分滞留在土层中，不易向下运输。杨宇等[21]研究表明，相比于未施加生化黄腐酸，施加生化黄腐酸能够显著增加土壤团粒结构含量，且施用时间越长，土壤的团粒结构含量越大。本试验结果表明，当生化黄腐酸施加量为8 g/kg时，入渗速率呈现增大的趋势，这可能是因为当生化黄腐酸施加量过多时自身会发生聚合吸水膨胀[31-32]，土壤孔隙增大，从而使得水分入渗速率加快。

2.2 生化黄腐酸对土壤水盐分布的影响

图3为入渗结束后不同生化黄腐酸施加量(0、1、2、4、8 g/kg)下土壤含水率分布曲线。由图3可知，土壤含水率随着土层深度的增加而降低，而施加生化黄腐酸可以提高土壤含水率，其中施加量4 g/kg下效果最为明显。在土层深度0、5、10、15、20、25、30 cm，施加量4 g/kg处理的土壤含水率分别高于对照13.07%、13.01%、14.11%、17.07%、23.08%、43.09%、86.79%。入渗结束后，与未施加生化黄腐酸相比，生化黄腐酸施加量为1、2、4、8 g/kg下的土壤剖面平均体积含水率分别增加了8.90%、17.70%、20.41%、11.67%。这是因为生化黄腐酸增加了土壤团粒结构含量，改善土壤结构，提高了土壤保水能力，然而当生化黄腐酸施加量过多会自身发生聚合吸水膨胀，扩大土壤孔隙，使土壤水分流失。

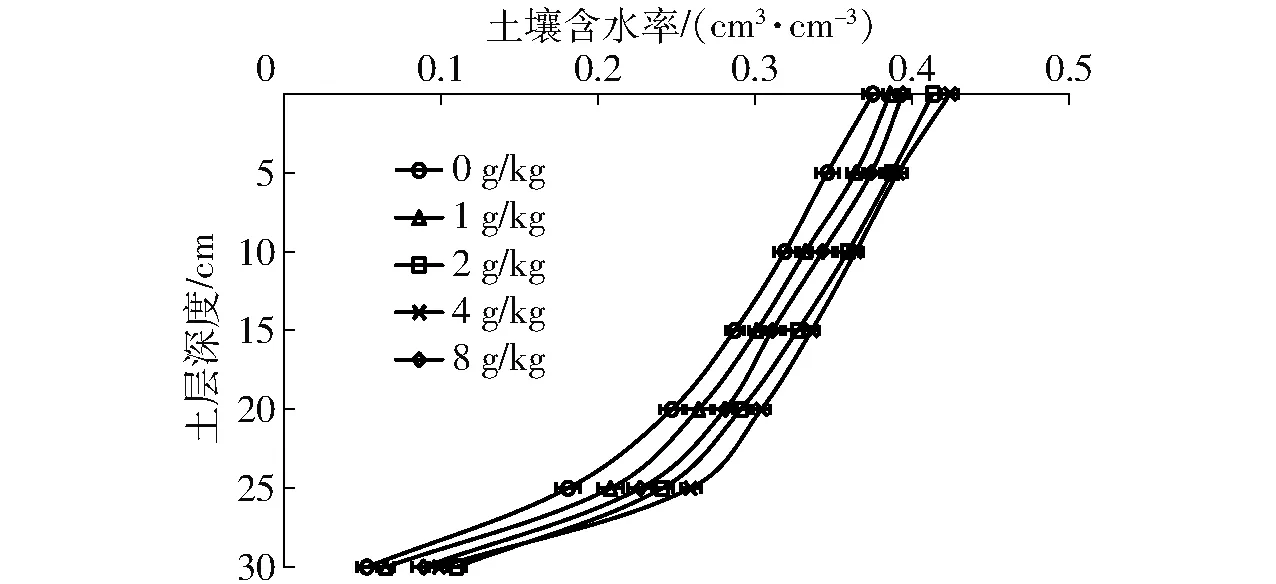
图3 不同生化黄腐酸施加量下土壤含水率变化曲线Fig.3 Variation curves of soil moisture content under different application amounts of BFA

图4为不同生化黄腐酸施加量(0、1、2、4、8 g/kg)下土壤含盐量分布曲线。由图4可知，由于淋洗作用，各处理的土壤含盐量会随着土层深度的增加而增加。入渗结束后，施加生化黄腐酸后的土壤含盐量和未施加生化黄腐酸后的土壤含盐量差值与未施加生化黄腐酸后的土壤含盐量相比，比值为正值时定义为相对脱盐率(%)，比值为负值时定义为相对积盐率(%)。各处理在土层0～30 cm范围脱盐效果和积盐效果不同，计算得出土层深度0～30 cm内，不同生化黄腐酸施加量下的土壤相对脱盐率和相对积盐率(表1)。在0～20 cm土层，与未施加生化黄腐酸相比，施加1、2、4、8 g/kg生化黄腐酸后的土壤平均相对脱盐率分别为5.29%、27.04%、42.77%、14.74%。而在20～30 cm土层，土壤含盐量则呈现出相反的变化趋势，说明盐分主要被淋洗到20 cm土层以下，施加生化黄腐酸1、2、4、8 g/kg后土壤平均相对积盐率分别为-14.84%、-39.06%、-60.05%、-23.66%，这说明生化黄腐酸具有抑制盐分在土壤表层积累的作用。主要原因可能是：施加生化黄腐酸处理的土壤水分入渗速率变慢，土壤中的盐分离子能更充分地溶解在水中，使随水向下运移的盐分增加；土壤累积入渗量的增加，也使得更多的水分参与洗盐过程中，增强了压盐效果；此外，生化黄腐酸的巨大比表面积[33]能对盐分离子产生表面吸附，同时其自身含有的羟基、羧基等活性功能团能够络合[34-35]土壤溶液中的盐分离子，使土壤表层盐分离子与生化黄腐酸一同随水向下运移。郑敏娜等[36]研究表明，黄腐酸能够显著提高土壤淋洗液中Na+含量；刘小媛等[37]研究表明，施加黄腐酸能够显著降低0～10 cm土壤处电导率。

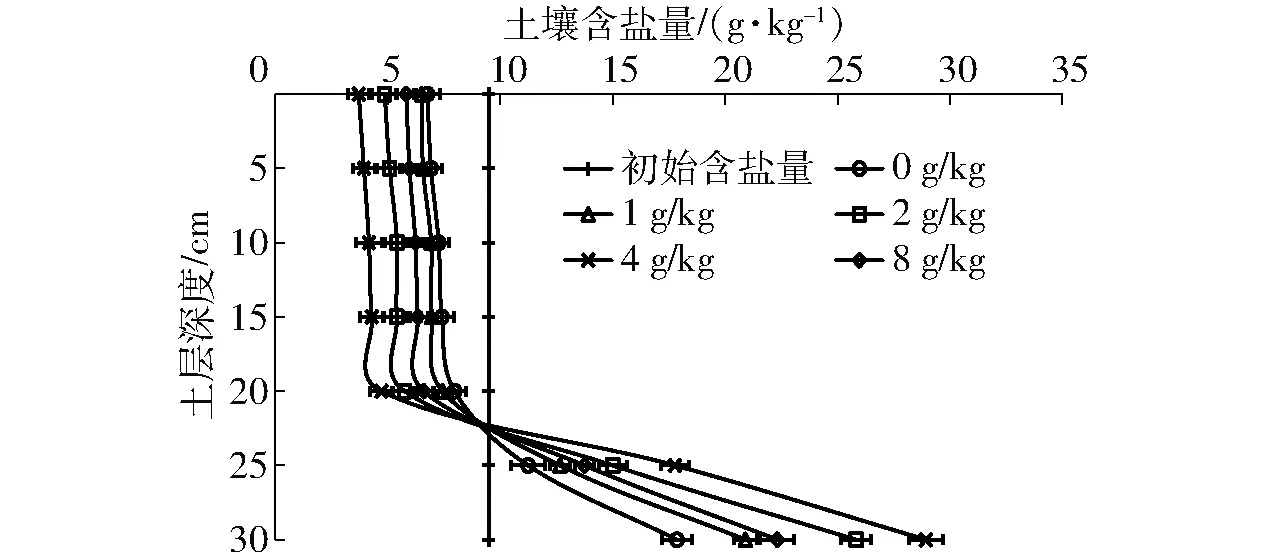
图4 不同生化黄腐酸施加量下土壤含盐量变化曲线Fig.4 Variation curves of soil salt content under different BFA application amounts

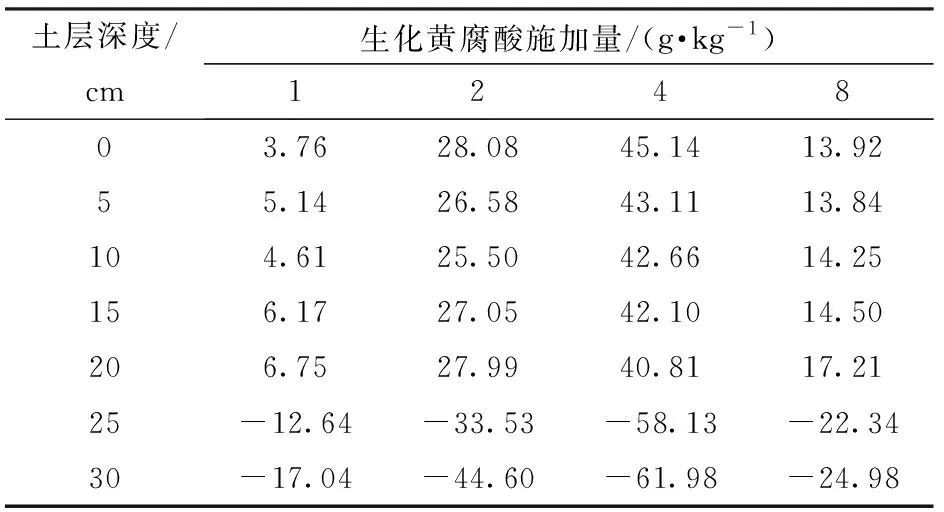
表1 不同生化黄腐酸施加量对脱盐效果的影响Tab.1 Effect of different application amounts of BFA on desalination %

2.3 生化黄腐酸对土壤水分特征曲线的影响

土壤水分特征曲线表征土壤水吸力与土壤含水率的关系，反映了土壤水能量与数量之间的关系，是研究土壤水分保持和运动的基本特性曲线[38]。不同生化黄腐酸施加量的水分特征曲线的反推结果如图5所示。由图5可知，当土壤含水率相同时，土壤水吸力随着生化黄腐酸施加量的增加呈现先增大后减小的趋势，其中施加量为4 g/kg的土壤水吸力最大，即向土壤中施入生化黄腐酸后能够使土壤基质势降低，土壤对水分的保持能力增强，这是由于生化黄腐酸可作为腐殖质中可溶于水且带负电荷的有机胶体施入土壤中，在胶结作用下使土粒、微团粒相互团聚，促进了土壤团粒结构的形成，改善了土壤结构，从而增强了土壤的保水性能。

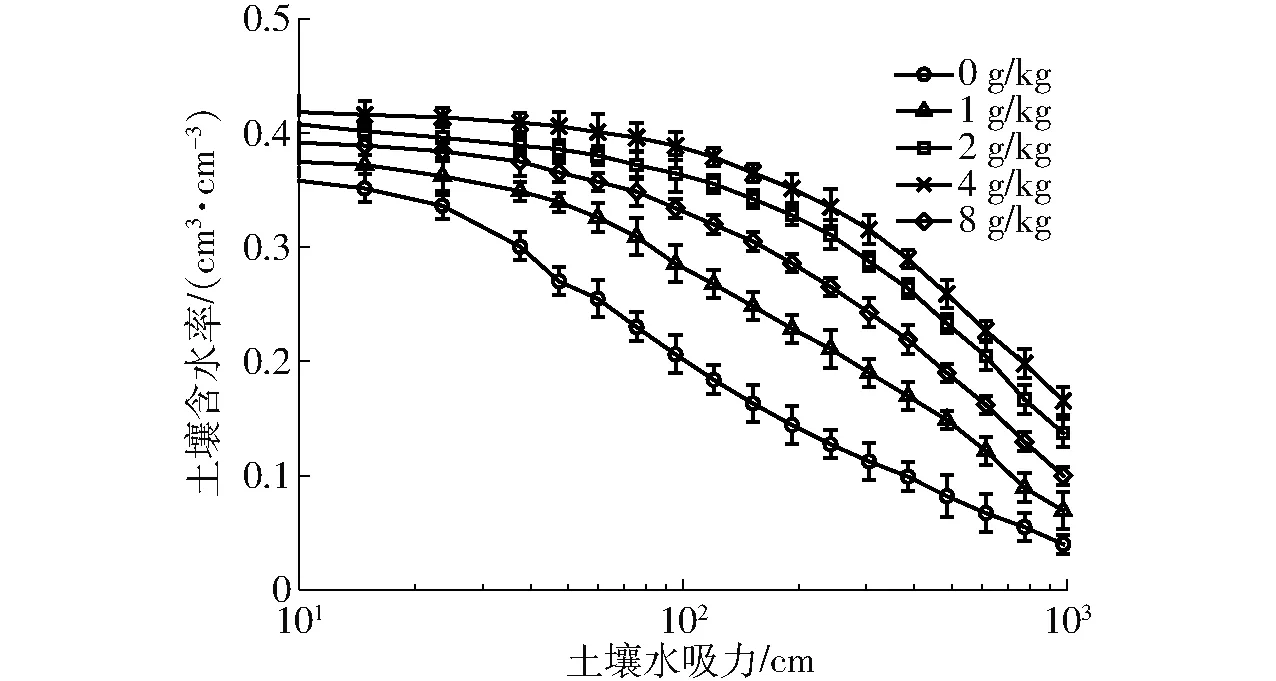
图5 生化黄腐酸施用量对土壤水分特征曲线的影响Fig.5 Effect of BFA on water characteristic curves

2.4 生化黄腐酸对入渗模型参数的影响

将不同生化黄腐酸施加量(0、1、2、4、8 g/kg)下累积入渗量与时间的关系、入渗率与概化湿润锋的关系、累积入渗量与湿润锋的关系分别采用Philip模型、Green-Ampt模型和代数模型进行拟合，各参数拟合结果如表2所示。由表2可知，各处理的决定系数R2均大于0.97，说明Philip模型、Green-Ampt模型和代数模型均能较好地模拟不同生化黄腐酸施加量下的土壤水分入渗规律。

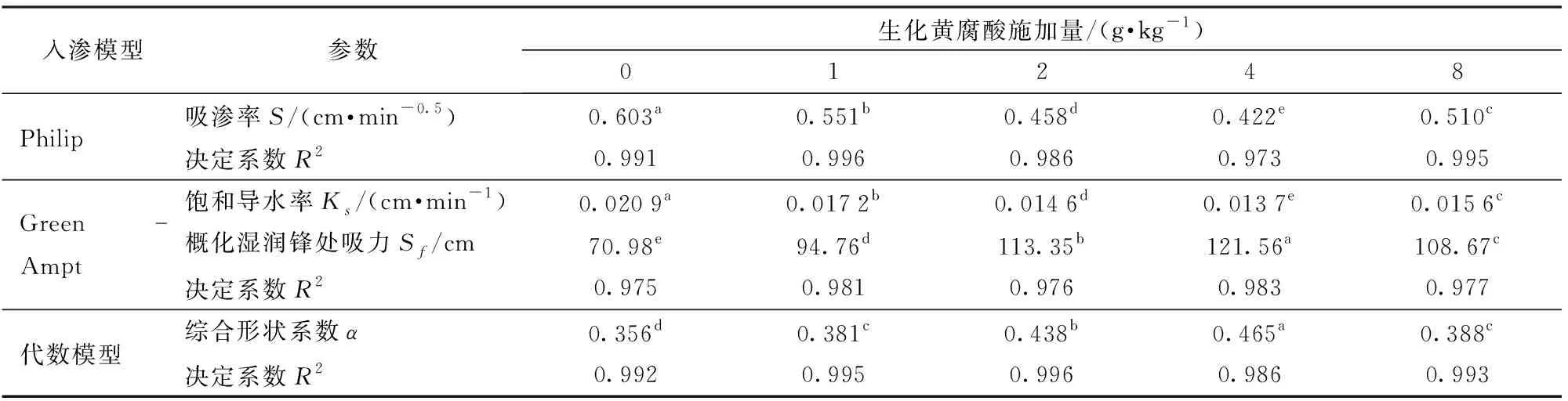
表2 不同生化黄腐酸施加量对入渗模型参数的影响Tab.2 Influence of different BFA application amounts on infiltration model parameters

吸渗率S表示土壤依靠毛管力吸收或释放水分能力[39]，将吸渗率S与生化黄腐酸施加量进行二次项拟合，拟合结果如图6所示。由图6可知，对于Philip入渗模型，吸渗率S随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，表明土壤入渗能力随生化黄腐酸施加量的增加先减小后增大，这与湿润锋和累积入渗量变化规律一致。当生化黄腐酸施加量为4 g/kg时，吸渗率S最小，低于对照组30.02%。

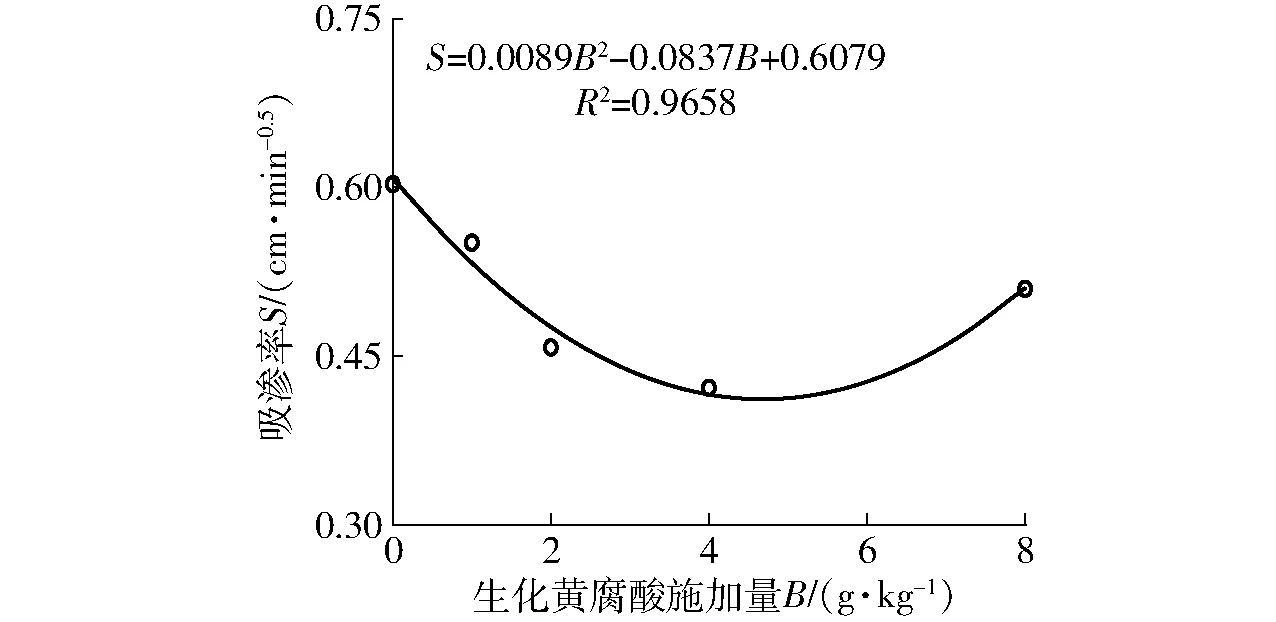
图6 生化黄腐酸施加量与吸渗率的关系曲线Fig.6 Relationship between application amount of BFA and sorptivety

对于Green-Ampt模型，饱和导水率Ks随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，在施加量为4 g/kg时，饱和导水率Ks最小，低于对照组58.79%。而概化湿润锋处吸力Sf则随着生化黄腐酸施加量的增加呈现先增大后减小的变化趋势，在施加量为4 g/kg时，概化湿润锋处吸力最大，高于对照组71.26%。将饱和导水率Ks和概化湿润锋处吸力Sf与生化黄腐酸施加量的关系进行拟合，拟合结果如图7所示。由图7可知，拟合R2均大于0.96，说明饱和导水率Ks和湿润锋处吸力Sf均与生化黄腐酸施加量之间呈较好的二次多项式关系。

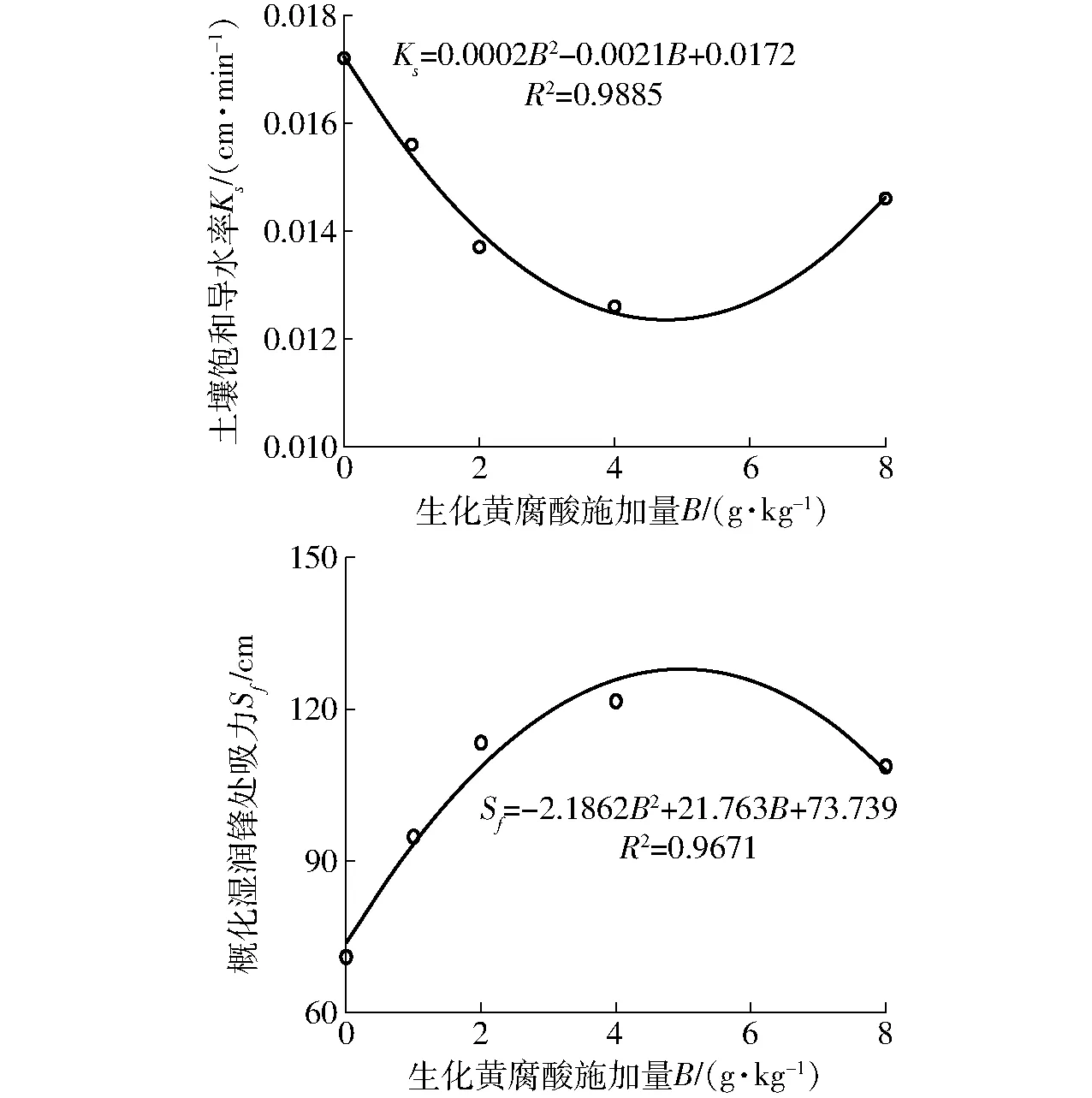
图7 生化黄腐酸施加量与饱和导水率和概化湿润锋处吸力的关系曲线Fig.7 Relationship between application amount of BFA and saturated hydraulic conductivity and suction at generalized wetting front

将土壤饱和导水率的实测值与拟合值进行拟合，结果如图8所示。由图8可知，实测值与拟合值存在较好的线性关系，决定系数R2为0.997，但实测值与拟合值之间仍存在一定的误差。诸多因素均可引起实测值和拟合值的误差，例如软件反推土壤模型参数时存在参数的置信度问题；测定土壤饱和导水率和水分入渗时的水温差异也会对测量值的准确度产生影响。

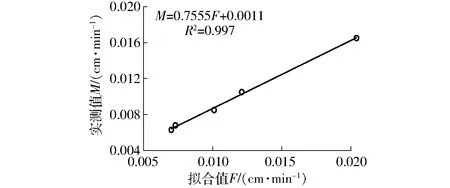
图8 各处理下土壤饱和导水率实测值与拟合值关系曲线Fig.8 Relationship between measured and fitted value of soil saturated hydraulic conductivity under each treatment

利用式(4)对比分析施加生化黄腐酸入渗条件下Philip入渗模型和Green-Ampt入渗模型参数之间的相互转换关系，结果如表3所示。由表3可知，两个入渗模型参数中S和KsSf的拟合值随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，且在施加量为4 g/kg时达到最小值，这与两个入渗模型参数的拟合值变化规律一致。然而拟合值和计算值存在相对误差，这是因为生化黄腐酸改善了土壤团粒结构，从而使得入渗公式参数发生变化，最终影响了Philip模型和Green-Ampt模型参数互相转换的精度。

表3 不同生化黄腐酸施加量对入渗模型拟合结果的影响Tab.3 Effect of different application amounts of BFA on fitting results of infiltration model

2.5 代数模型描述土壤施加生化黄腐酸入渗后土壤含水率准确性分析

将拟合得到的综合形状系数α利用式(6)计算土壤含水率，图9为土壤含水率计算值和实测值之间的关系。由图9可以看出，土壤含水率计算值与实测值之间吻合程度较好。为了更好地说明代数模型的计算效果，对土壤含水率计算值和实测值之间进行误差分析。结果表明，随着生化黄腐酸施加量的增加，各处理的平均绝对误差分别为 1.36%、1.19%、3.15%、3.52%、2.04%。由此可见，代数模型能够较好地模拟计算施加生化黄腐酸后一维垂直入渗条件下的土壤含水率。

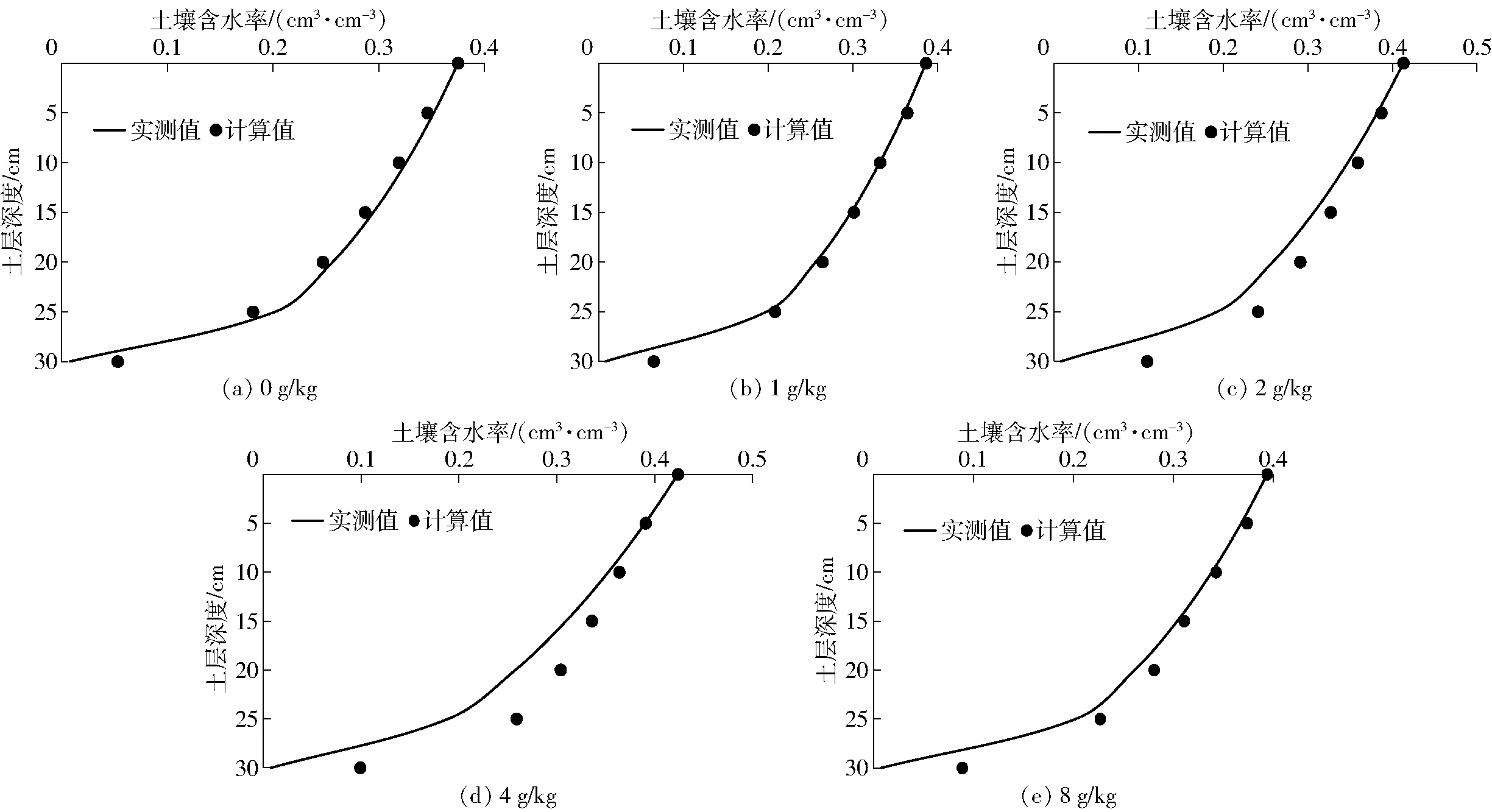
图9 土壤含水率计算值与实测值Fig.9 Theoretical and measured values of soil moisture content

3 结论

(1)生化黄腐酸具有减缓水分入渗速率的作用。施加生化黄腐酸后，相同时间内能够降低湿润锋运移速率；而当湿润锋深度相等时，生化黄腐酸能够增大累积入渗量。相同时间内，湿润锋深度随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，在施加量为4 g/kg时湿润锋深度最小。入渗至相同湿润锋时，土壤累积入渗量随着施加量的增加呈现先增大后减小的变化趋势，在施加量为4 g/kg时土壤累积入渗量最大。

(2)生化黄腐酸具有保水脱盐的作用。入渗结束后，与未施用相比，施加生化黄腐酸能够提高土壤含水率，且土壤含水率随着施加量的增加呈现先增大后减小的变化趋势，施加量为4 g/kg时土壤含水率最大。同时在土层0～20 cm，施加生化黄腐酸能够提高土壤脱盐率，与未施加相比，施加生化黄腐酸1、2、4、8 g/kg后的土壤平均脱盐率分别为5.29%、27.04%、42.77%、14.74%，其中施加量为4 g/kg时土壤脱盐效果最好。

(3)Philip模型、Green-Ampt模型和代数模型均能较好地模拟不同生化黄腐酸施加量下土壤水分入渗规律。吸渗率S和饱和导水率Ks随着生化黄腐酸施加量的增加呈现先减小后增大的变化趋势，施加量4 g/kg时S、Ks最小。概化湿润锋处吸力Sf和综合形状系数α随着生化黄腐酸施加量的增加呈现先增大后减小的变化趋势，施加量4 g/kg时Sf、α最大，且代数模型能够较为准确地拟合施加生化黄腐酸一维垂直入渗条件下的土壤含水率。